带红利和交易成本的欧式期权三叉树定价

茹琴

摘要：文章考虑按已知红利率和交易成本比例以及按固定红利额和交易成本额支付一次红利和交易成本，分别推导出含红利和交易成本的三叉树模型，通过矩阵算法计算该模型下期权的理论价格，并选取2020年9月25日至2020年12月23日上证50ETF三份认购期权合约的交易数据，对上述模型进行检验，结果表明，考虑红利率和交易成本比例的三叉树模型能够较好地反映市场的真实情况，且精确度高于考虑固定红利额和交易成本额的三叉树模型和不含红利和交易成本的三叉树模型。

关键词：欧式期权；三叉树；红利；交易成本

一、引言

近年来，我国金融市场发展迅速，市场规模不断壮大，投资者对金融衍生产品的需求日益强烈。期权作为一种金融衍生产品，自1973年期权定价公式出现以来，日渐成为交易者投资决策时获取利益信心的产品之一，在增强金融市场的稳定性和流动性等方面都具有重要意义，因此期权定价是否合理显得至关重要。随着金融市场的迅速发展，期权的定价模型也在不断地更新与修正，目前已有很多发展比较成熟的期权定价模型，二叉树模型就是其中之一。该模型最早是在1979年由Cox等提出，此后因应用简单高效得到了快速发展，随之而来的问题是该模型在实际应用中存在模型误差。为了解决二叉树定价方法的精确度问题，1986年，Boyle P P在二叉树模型的基础上进行拓展，提出了三叉树模型，随后Ahn等证明了三叉树定价模型的收敛效果以及精确性。目前有关二叉树和三叉树期权定价模型的研究很少有考虑支付红利和交易费用的情况，具体来说，张铁借助随机误差校正的方法构造出了精确度较高的新型二叉树参数模型。韩立杰等利用矩的思想构造出了B-S定价公式Δt上一阶近似的新型三叉树模型定价公式。宫文秀等给出了复合期权三叉树模型，并结合实例分析了相关影响变量的敏感度。李昊轩等借助随机方程和原点矩思想，在二叉树模型的基础上，给出了三叉树模型参数和期权价格的递推表达，证明了三叉树模型的收敛性和稳定性更好。然而，实际的金融市场中，股票交易需要支付红利和交易成本，因此在期权的定价模型中需要融入交易成本和红利以适应金融市场的实际情况。任芳玲等基于经典的B-S-M模型，考虑交易费用，并利用模型的解析式法，二叉树定价方法以及三叉树定价方法计算期权价格。宫文秀等在传统的三叉树定价方法基础上，引入CARCH模型，给出了随机市场模型下支付固定比例红利和交易费用的欧式看涨期权的三叉树模型。

现有文献中，将交易成本和红利融入三叉树期权定价模型中的研究较少。因此，本文考虑支付一次红利和交易成本，推导出含有交易成本和红利的欧式期权的三叉树模型，使该定价方法更符合金融市场的实际情况，并借助矩阵算法计算期权价格，最后通过选取上证50ETF三份认购期权的实际交易数据，对文中模型进行分析和检验。

二、模型说明

（一）三叉树模型

三叉树模型是在二叉树模型基础上的扩展延伸，与二叉树模型的定义类似，不同于二叉树模型的是，在期权有效期的每个时间段的节点上，期权价格的变化有三种可能：上升、持平和下降。如图1所示，标的资产在交易过程中有不确定的三种变化值uS、mS以及dS。

其中，u，m，d满足d<m=1<u。假设股票价格上升的概率为pu，下降的概率为pd，保持不变的概率为pm，且概率测度需满足：

pu+pm+pd=1

将期权的有效期[0，T]分为N个长度为Δt（Δt＝T/N）的相等时间段，股票的初始价格为S0，i为第i（1≤i≤N）个时刻，j表示对应时刻第j（1≤j≤2i-1）个支点，则在结点（i，j）处的股票价格为：

Si，j＝S0ui-1dj-1

其中，1≤i≤N，1≤j≤2i-1。在不考慮支付红利和交易成本时，令欧式期权的到期日为，到期日执行价格为K，fi，j为iΔt时刻在结点（i，j）的期权价格，则欧式看涨期权的价格为：

fN，j＝max（0，S0uN-1dj-1-K），0≤j≤2N-1

在风险中性概率测度p下，可得到在任意结点（i，j）的风险中性定价公式：

fi，j=e-rΔt[pufi+1，j+pmfi+1，j+1+pdfi+1，j+2]

上述两式中的参数满足：

pu=■，

pm=■

pd=■，

u=M+■，d=M-■

其中，r为无风险收益率，σ为标的资产波动率，M＝■。

（二）已知红利率和交易成本比例的三叉树模型

期权在实际的金融市场交易中，往往会支付红利和交易费用，支付红利会引起股票价格下降，支付交易费用会引起股票价格上升，股票价格下降和上升的幅度分别为每股股票支付红利和交易费用的金额，依据金融市场交易规律，由红利引起的股票价格下跌的幅度往往要高于由交易费用引起的股票价格上涨的幅度。假设有效期内期权仅支付一次红利和交易成本，红利率为δ，交易成本收取比例为k，在除息日这一时刻结点，按照上述方法可以得到：

除息日之前结点（i，j）的股票价格为：

Si，j＝S0ui-1dj-1

除息日之后结点（i，j）的股票价格为：

Si，j＝S0（1-δ+k）ui-1dj-1

如果有效期内期权支付多次红利，且除息日在结点（i，j）之前，令δi为时刻i之前所有除息日支付红利的红利率总和，结点（i，j）相对应的股票价格为：

Si，j＝S0（1-δi+k）ui-1dj-1

对上述模型使用矩阵算法进行计算，考虑仅支付一次红利和交易成本，红利率为δ，固定交易成本比例为k，则参照文献可以得出如下定理：

定理1：到期日之前按照已知的红利率δ和固定交易比例k支付一次红利和交易成本，则欧式期权价格在时刻tN有2N-1种可能，分别为：

fN，1，fN，2，…，fN，2N-1

令行矩阵F＝（fN，1，fN，2，…，fN，2N-1），G为2N-1阶矩阵，设

G＝p■  0  … 0 0 0p■ p■ … 0 0 0p■ p■ … 0 0 00  p■ … 0 0 0┆┆？埙 ┆┆┆0  0 … p■ 0 00  0 … p■ 0 00  0 … p■ 0 0

则T1时刻期权的价格为：f=e-rNΔtFG■■，其中G■■为G的N次幂的第一列。

证明 由三叉树方法可知TN-1时刻各结点的期权价格：

结点（N-1，1）的期权价格为：

fN-1，1＝e-rΔt[pufN，1+pmfN，2+pdfN，3]=e-rΔt（fN，1，fN，2，fN，，3，fN，4，…，fN，2N-1）（pu，pm，pd，0，…，0）T

结点（N-1，2）的期权价格为：

fN-1，2＝e-rΔt[pufN，2+pmfN，3+pdfN，4]=e-rΔt（fN，1，fN，2，fN，，3，fN，4，…，fN，2N-1）（0，pu，pm，pd，0）T

以此类推，结点（N-1，2N-3）的期权价格为：

fN-1，2N－3＝e-rΔt[pufN，2N-3+pmfN，2N+pdfN，2N-1]

=e-rΔt（fN，1，fN，2，fN，，3，fN，4，…，fN，2N-1）（0，…，0，pu，pm，pd）T

综合可得，

（fN-1，1，fN-1，2，…，fN-1，2N－3，0，0）＝e-rΔtFG1

继续按照结点（N-1，1）的方法推导出结点TN-2时刻各节点的期权价格。

结点（N-2，1）的期权价格为：

fN-2，1＝e-rΔt[pufN-1，1+pmfN-1，2+pdfN-1，3]=e-rΔt（fN-1，1，fN-1，2，fN-1，3，fN-1，4，…，fN，2N－3，0，0）（pu，pm，pd，0，…，0）T

结合TN-1时刻各节点的期权价格可得

fN-2，1＝e-2rΔtFG1（pu，pm，pd，0，…，0）T

同理可得：

fN-2，2N－5＝e-2rΔtFG1（0，…，0，pu，pm，pd）T

整理得：

（fN-2，1，fN-2，2，…，fN-2，2N-5，*，*，0，0）＝e-2rΔtFG2

TN-2时刻共有2N-5个节点，因此只需考虑（fN-2，1，fN-2，2，…，fN-2，2N-5），*表示的内容不在本文考虑范围内，故没有展示具体内容。继续向前推导每个时刻各节点的期权价格，最终可以得到T1时刻节点（1，1）的期权价格为：

（f1，1，*，…，*，0，0）＝e-NrΔtFGN

*表示的内容不在研究范围内，因此，可以得到T1时刻期权的价格为：

f＝e-NrΔtFG1N

其中，G1N为G的N次幂的第一列。则欧式看涨期权定价公式为：

fN，j＝max（S0（1-δ+k）uN-1dj-1-K，0）

其中，fN，j可由定理1中行矩阵F的各元素确定。如果期權在有效期内多次支付红利，可按上述算法进行计算，即将一次支付红利率δ替换为多次支付红利率总和δi即可。

（三）已知红利额和交易成本额的三叉树模型

假设期权在有效期内按已知的数额支付红利和交易成本，则三叉树图在支付红利和交易成本后的树枝不再重合，若考虑支付多次红利，需考虑的结点数过多，过程较为繁琐，因此本文仅考虑支付一次红利和交易成本。令股票的波动率σ为常数，除息日τ在时刻lΔt和（l+1）Δt之间，支付红利数额为D，支付交易成本数额为H，这时任意结点（i，j）处期权的价值需要从以下几点来考虑。

1.当i≤l时，此时未到除息日τ，因此不需要考虑支付红利和交易成本，任意结点相对应的股票价格为：

Si，j＝S0ui-1dj-1，1≤j≤2i-1

2.当i=l+1时，此时已在除息日支付红利和交易成本，任意结点相对应的股票价格为：

Si，j＝S0ui-1dj-1-D+H，1≤j≤2i-1

3.当i=l+2时，此时任意结点对应的股票价格应基于支付红利和交易成本后的股票价格来计算，股票价格为：

u（S0ui-1dj-1-D+H），S0ui-1dj-1-D+H和d（S0ui-1dj-1-D+H）

其中1≤j≤2i-1，此时，三叉树将有3（i+1）个结点而不是2i-1个结点。则在（l+m）Δt时刻，将有（2m-1）（2l-1）个结点而不是2（l+m）-1个结点。由于支付红利和交易成本后，树枝不再重合，为解决这一问题，可将股票价格考虑为由两部分组成，一部分考虑为不确定的股票价格，另一部分考虑为有效期内期权支付红利和交易成本决定的股票价格。令不确定的股票价格为S*，此时股票价格的波动率σ*为常数，在期权的有效期内有个除息日τ，且lΔt≤τ≤（l+1）Δt，则在任意时刻iΔt时刻，不确定的股票价格S*为：

S*=S，iΔt＞τS*＝S-（D-H）e-r（τ-iΔt），iΔt≤τ

通过这种方法可以将支付的红利和交易成本加在每个节点的股票价格上，这样就可以恢复原来三叉树的重合状态，iΔt时刻恢复2i-1个结点。此时，在iΔt时刻，任意结点所对应的股票价格可由下面的公式给出。

当时刻iΔt在除息日τ当日或之前，即iΔt≤τ，任意结点股票价格为：

S*ui-1dj-1+（D-H）e-r（τ-iΔt），j=1，2，…，2i-1

当时刻iΔt在除息日τ之后，即iΔt＞τ，任意结点股票价格为：

S*ui-1dj-1，j=1，2，…，2i-1

定理2：按已知数额D和H支付一次红利和交易成本，则欧式期权价格在tN时刻的2N-1种可能，分别为：

fN，1，fN，2，…，fN，2N-1

行矩阵F和2N-1阶下三角矩阵G与定理1一致，则在T1时刻期权的价格为：

f=e-NrΔtFG■■

其中，G■■为下三角矩阵G的N次幂的第一列。该定理的证明过程和定理1一致，在此不作重复证明。在到期日T，欧式看涨期权的定价公式为：

fN+1，j＝max（■-K，0），j=1，2，…，2N-1；

其中，■的定义和上文一致，由不确定的股票价格S*确定，公式如下：

■＝S*ui-1dj-1+（D-H）e-r（τ-iΔt），iΔt≤τS*ui-1dj-1，iΔt＞τ。

三、实证分析

（一）变量选取及数据说明

本文采用上证50ETF期权的实际交易数据对上述模型进行实证分析，选择样本区间为期权持有期是2020年9月25日至2020年12月23日的三份认购期权合约，分别为50ETF购12月3844A、50ETF购12月3746A以及50ETF购12月3647A，数据均来源于东方财富Choice金融终端。根据上述模型可知，期权价格主要受标的资产价格S，期权执行价格K，到期日T，无风险利率r，标的资产波动率σ，红利以及交易成本的影响。

1.标的资产价格S。本文选取样本区间内三份认购期权所对应的标的资产在交易日的收盘价作为标的资产价格S，选取三份认购期权每日的收盘价作为期权的实际市场价格。例如，2020年10月15日标的资产收盘价为3.4250元，则S＝3.4250。

2.期权执行价格K。三份认购期权的执行价格分别为3.8440，3.7460以及3.6740。

3.到期日T。本文选取的样本区间共58个交易日，上证50ETF期权一年大约有250天交易日，令Δt为期权上市的交易天数，则到期日为：

T＝■

4.无风险利率r。本文选取和期权样本同期的上海銀行间同业拆放利率6个月期shibor利率的平均值作为无风险利率r，经过计算，无风险利率r的年化利率为2.9%。

5.标的资产波动率σ。本文的标的资产波动率采用历史波动率，即选取样本区间第一天之前的58天的数据来计算标的资产波动率，计算公式如下：

σ＝■×■

其中，μi=ln（Si/Si-1），i=1，2，…，n，n＝58。根据公式计算出标的资产的历史波动率约为0.222。

6.红利。样本区间内红利的除息日为2020年11月30日，每份分红为0.051元。红利率为红利和标的资产价格的比值，标的资产价格本文选取除息日标的资产的收盘价格，计算出红利率为1.5%。

7.交易成本。本文选取上证50ETF期权的基金运作费用率0.6%作为交易成本比例，选取样本区间内标的资产的均值和基金运作费用率的乘积作为交易费用，计算结果为0.021。

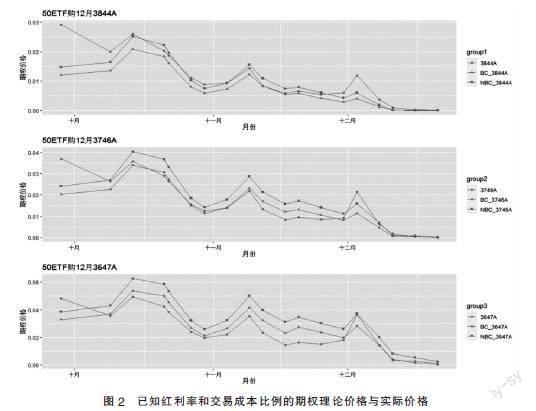
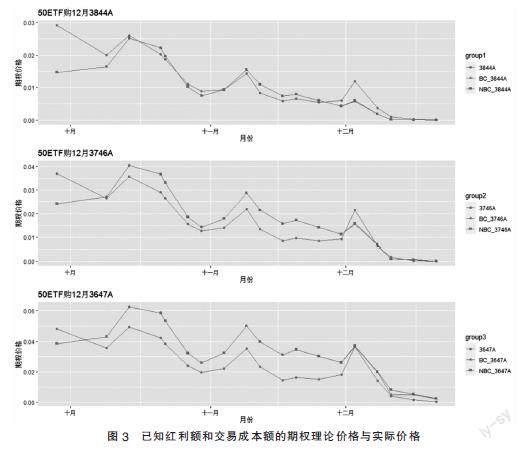
（二）上证50ETF期权理论价格

根据对各参数的介绍，分别计算出所取样本含红利和交易费以及不含红利和交易费的期权价格，并与实际的市场价格进行比较，三份认购期权的理论价格与实际价格比较折线图如图2和图3所示，BC表示含有红利和交易成本的期权理论价格，NBC表示不含红利和交易成本的期权理论价格，从中可以看出，无论是已知红利率和交易成本比例，还是已知红利额和交易成本额，三份认购期权考虑红利和交易费用的理论价格以及不考虑红利和交易费用的理论价格均能较好地贴近实际价格，且价格的变化趋势基本一致，也可以清晰地看出，考虑已知红利率和交易成本比例的三叉树期权定价模型可以贴近上证50ETF期权的实际价格，说明在实际的金融市场中，红利和交易费用会影响期权的定价。

（三）误差分析

除了折线图直观的描述之外，还可以通过误差分析来说明含红利和交易费用期权定价模型的效率。本文主要选取以下三种误差来进行分析，假设期权的实际价格为Pactual，期权的理论价格为Ptheory，样本量为，则可以得到以下误差分析公式：

1.平均绝对误差（MAE）

MAE=■■｜P■-P■｜

2.平方绝对百分比误差（MAPE）

MAPE=■■｜■｜×100%

3.均方根误差（RMSE）

RMSE=■

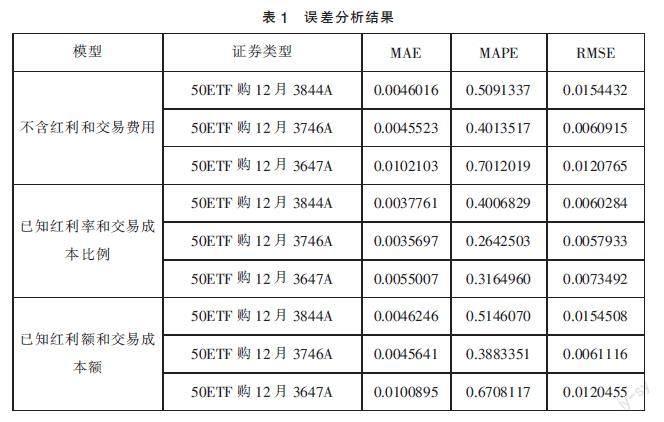
根据上述三个误差公式，对含红利和交易费用的期权定价模型以及不含红利和交易费用的期权定价模型计算出的理论价格分别进行误差分析，结果如表1所示。

MAE，MAPE以及RMSE主要衡量的是期权的实际价格与理论价格之间偏差的大小，值越小说明模型的精确度更高。从表1中可以看出，三份认购期权考虑红利率和交易成本比例的理论价格的误差均小于不含红利和交易成本的理论价格的误差，说明在对上证50ETF进行定价时，考虑红利率和交易成本比例的定价模型精确度更高。也同样可以看出考虑红利额和交易成本额的定价模型的精确度要低于考虑红利率和交易成本比例的定价模型。

四、结语

本文在传统三叉树期权定价方法的基础上，考虑支付一次分红和交易成本，推导出含有红利和交易成本的欧式期权的三叉树定价方法，再结合矩阵算法，得到了欧式期权价格基于三叉树期权定价模型的数值求解方法。最后，本文选取2020年9月25日至2020年12月23日上证50ETF三份认购期权合约的交易数据，对其进行实证分析，结果表明，考虑红利率和交易成本比例的三叉树定价方法可以较好地贴近期权的实际市场价格，更符合市场的真实情况，考虑红利额和交易成本额的三叉树定价方法相对来说贴合度较弱，三种误差MAE，MAPE以及RMSE也进一步表明考虑红利率和交易成本比例的三叉树定价方法的精确度优于不含红利和交易成本的三叉树定价方法以及考虑红利额和交易成本额的三叉树定价方法。

参考文献：

[1]COX J C， ROSS S A， RUBINSTEIN M.Option pricing： a simplified approach[J].Journal of Financial Economics，1979，7（03）：229-263．

[2]Boyle P P.Option Valuation Using a Tree-Jump Process[J].International Options Journal，1986，3：7-12．

[3]Ahn J，Song M.Convergence of the Trinomial Tree Method for Pricing European/American Options[J].Applied Mathematics and Compution，2007，189（01）：575-582.

[4]张铁.一个新型的期权定价二叉树参数模型[J].系统工程理论与实践，2000，20（11）：90-93.

[5]韩立杰，刘喜波，刘宇.期权定价的新型三叉树方法[J].数学的实践与认识，2007，37（18）：39-42.

[6]宫文秀，高凌云.复合期权的三叉树模型[J].统计与决策，2016（18）：83-86．

[7]李昊轩，贺钰淇，张昊阳，解菲.基于Vasicek随机利率模型的美式期权三叉树定价[J].中国商论，2020（16）：44-47.

[8]任芳玲，薛盼红.考虑交易费用和泊松过程的沪深300股指期权定價研究[J].湖北大学学报（自然科学版），2018，40（04）：327-332.

[9]宫文秀，许作良.基于CARCH模型的三叉树期权定价方法[J].数学的实践与认识，2020，50（07）：106-114.

[10]覃思乾.基于二叉树模型期权定价的矩阵形式算法[J].广西师范学院学报，2006，23（01）：26-30.

（作者单位：湖北工业大学理学院）