深度学习方法求解中子输运方程的微分变阶理论

刘 东,王雪强,张 斌,俞蔡阳,宫兆虎,陈奇隆

(1.中国核动力研究设计院,四川 成都 610213;2.中核核能软件与数字化反应堆工程技术研究中心,四川 成都 610213;3.四川大学 计算机学院,四川 成都 610065)

在反应堆中子物理学领域,求解中子输运方程是反应堆物理计算的基本问题,对反应堆工程的堆芯设计研发与运行支持具有至关重要的作用。求解输运方程的传统方法是以离散纵标法(SN)、特征线法(MOC)为代表的确定论方法[1-2],和以蒙特卡罗方法为代表的统计学方法[3]。这些方法总体思路是从方程能量离散、空间离散、角度离散、并行加速等方面开展研究,从而获得输运方程的数值解。传统方法各有特点,互为补充,在实际工程中已得到大量成功应用。

近年来,随着以深度学习为代表的新一代人工智能技术的发展,利用深度学习技术求解复杂偏微分方程的方法正成为数值计算领域前沿研究热点[4]。不同于传统的数据驱动机器学习方法,基于物理信息的神经网络(PINN)等深度学习框架[5]不需要预先收集大量数据作为机器学习的训练集,可直接正向求解复杂高阶多维方程,并具有空间几何限制少、边界条件处理灵活、计算流程规范性好、实验数据同化能力强等特点,已在求解热工水力N-S方程等多个领域取得了重要突破[5-6]。在求解反应堆中子扩散方程领域也取得了系列进展[7-10],这为中子输运方程的求解开辟了一条新的潜在技术途径,越来越受到业界的重视。

当前深度学习技术成功求解的方程类型是微分方程[5-10],而中子输运方程具有微分-积分方程的特点,其存在能量、角通量密度表示的中子散射与裂变多重定积分项,这造成了直接将现有方法应用到中子输运方程时存在很大困难。针对该问题,文献[11]参考传统SN方法[1-2],将定积分项的被积角度变量进行离散,通过高斯求积组[1-2]构造定积分项的近似离散和,形成损失函数进行机器学习,并给出了瞬态情况下一维几何的离散时间、角度标通量密度计算结果。

本文基于深度学习技术求解微分方程的基本方法,针对中子输运方程存在积分项的特点,提出求解中子输运方程的微分变阶理论,将角通量密度定积分变换为其对应的高阶微分形式原函数进行深度学习,成功后再降阶为原输运方程,从而为解决输运方程多重积分项带来的深度学习方法困难探索新技术途径,并可获得完整的几何-角通量密度连续性计算结果。

1 中子输运方程的各种形式

中子输运方程的完整形式参考文献[1],其离散能群、裂变源/散射源各向同性的稳态输运方程在不考虑外源下的形式为:

(1)

式中:φ(r,Ω)为在r位置处角度为Ω的中子角通量密度,m-2·s-1;Σt为总反应截面,m-1;Σs为散射截面,m-1;ν为每次裂变放出的平均中子数;xg为裂变中子的能谱分布;Σf为裂变截面,m-1;keff为有效增殖因数;g为分段能群编号,g=1,2,…,G。

当考虑中子能量为单能时,式(1)简化为:

(2)

特别地,式(2)的平板几何形式[2]为:

(3)

式中:x为平板厚度;μ为直角坐标下的方向余弦,其详细定义参考文献[1-2]。

式(2)的球几何形式[2]为:

(4)

式中:r为球半径;μ为球坐标下的方向余弦,其详细定义参考文献[1-2]。

式(2)的无限圆柱几何形式[2]为:

(5)

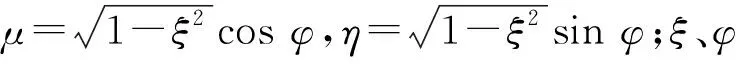
式(2)～(5)可描述为统一的偏微分-积分方程形式[12]:

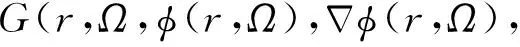
(6)

2 微分变阶理论基本原理

深度学习技术求解输运方程的微分变阶理论基本原理是:利用微积分数理方法对中子输运方程进行微分升阶,将其变换为关于角通量密度积分原函数表示的高阶微分方程,进而用原函数线性组合形式消除输运方程角通量密度定积分项;同时,给出微分升阶后的原函数特定解形成方法,确定不同角通量密度积分形式对应的原函数定解约束,并将输运方程的边界条件映射为原函数表示的边界条件;以微分升阶变换后的原函数为目标,将控制方程残差、边界条件、原函数定解条件以及特征值约束加权形成统一损失函数进行深度学习,待神经网络函数逼近原函数,可获得原函数的数值解;此后,将原函数关于通量密度角度变量进行求导实现微分降阶,即得到原中子输运方程的角通量密度函数分布,从而实现利用深度学习技术求解中子输运方程。

为简化起见,以单能临界、稳态具有一维/二维角通量密度形式的中子输运方程为对象进行详细讨论,其他形式输运方程包含的角通量密度定积分项形式在数理方法上与其一致,可直接类推。

式(1)角通量密度φ(r,Ω)关于角度变量Ω为连续函数[1-3],按照微积分学原理[13],其存在关于角度变量Ω积分原函数F(r,Ω),由牛顿-莱布尼兹公式可表示如下。

1)Ω为一元变量

用方向余弦μ表示Ω[13],有:

F(r,μ1)-F(r,μ0),

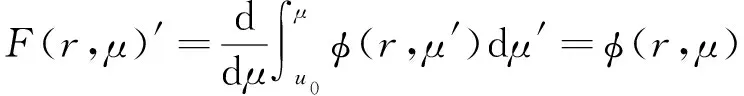
(7)

式中,μ1、μ0分别为定积分项中Ω′积分上下限。

2)Ω为二元变量

用方向余弦ξ、幅角φ表示Ω[14],有:

F(r,ξ1,φ1)-F(r,ξ0,φ1)-

F(r,ξ1,φ0)+F(r,ξ0,φ0),

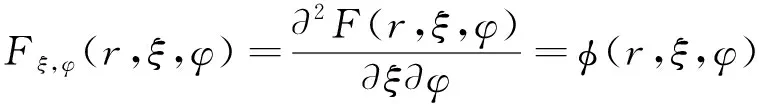
(8)

式中,ξ1、ξ0和φ1、φ0分别为方向余弦ξ、幅角φ表示的定积分项中Ω′积分上下限。

(9)

据此给出平板几何、球几何、圆柱几何微分升阶后的由原函数表示的输运方程形式,其他几何形式的方程可据此类推。

1) 平板几何微分升阶形式

将式(7)代入式(3),并令μ1=1,μ0=-1,则有:

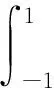
(10)

2) 球几何微分升阶形式

将式(7)代入式(4),并令μ1=1,μ0=-1,则有:

(F(r,1)-F(r,-1))

(11)

3) 无限圆柱几何微分升阶形式

将(8)式代入(5)式,并令ξ1=1,ξ0=0,φ1=π,φ0=0,则有:

F(r,0,π)-F(r,1,0)+F(r,0,0),

(F(r,1,π)-F(r,0,π)-F(r,1,0)+F(r,0,0))

(12)

3 原函数确定解生成方法

根据微积分的性质,同一连续函数的积分原函数为一簇函数[13],若不确定特定的原函数进行深度学习,则深度学习方法难以收敛,以下分别就中子通量密度的角度Ω为一维与二维情况进行讨论,给出原函数确定解的方法。

3.1 Ω为一维变量

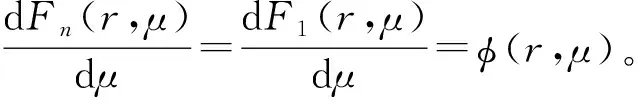
设μ0为任意固定角度变量,令Cn=-F1(r,μ0),则有特定的确定原函数:

F0(r,μ)=F1(r,μ)-F1(r,μ0)

(13)

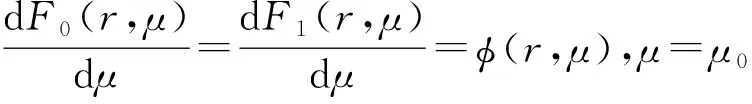
由此,原函数簇Fn(r,μ)在μ满足定解约束条件下,找到了一个确定的原函数F0(r,μ)。

针对式(10),令μ0=-1,则Cn=-F1(x,-1)。根据式(13)有F0(x,-1)=0,将式(13)确定的原函数F0(x,μ)及相关关系代入式(10),得到升阶形式平板几何方程为:

(14)

此时,原函数定解约束条件是μ0=-1,F0(x,-1)=0。

同理,式(13)代入式(11),升阶形式球几何方程变为:

(15)

此时,原函数定解约束条件是μ0=-1,F0(r,-1)=0。

3.2 Ω为二维变量

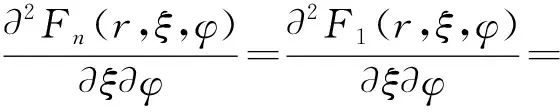
设ξ0、φ0为任意固定角度变量,令Kn(r,ξ)=-F1(r,ξ,φ0),Jn(r,φ)=-F1(r,ξ0,φ),Mn(r)+Cn=F1(r,ξ0,φ0),则有特定的确定原函数:

F0(r,ξ,φ)=F1(r,ξ,φ)-F1(r,ξ0,φ)-

F1(r,ξ,φ0)+F1(r,ξ0,φ0)

(16)

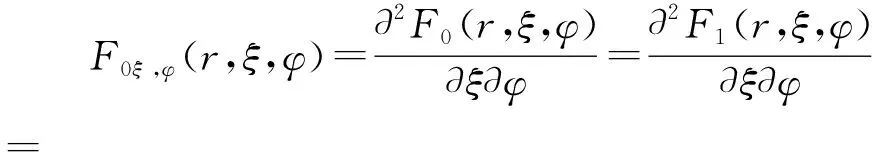
由此,就为原函数簇Fn(r,ξ,φ)在ξ、φ满足定解约束条件下找到了一个确定的原函数F0(r,ξ,φ)。

针对式(12),令ξ0=0,φ0=0,则Kn(r,ξ)=-F1(r,ξ,0),Jn(r,φ)=-F1(r,0,φ),Mn(r)+Cn=F1(r,0,0)。根据式(16)有F0(r,0,φ)=0及其特例F0(r,0,π)=0,F0(r,ξ,0)=0及其特例F0(r,1,0)=0,F0(r,0,0)=0。将式(16)中确定的原函数F0(r,ξ,φ)及相关关系代入式(12),升阶形式无限圆柱方程变为:

F0(r,1,π)

(17)

此时,原函数的定解约束项为:ξ0=0,F0(r,0,φ)=0;φ0=0,F0(r,ξ,0)=0;ξ0=0,φ0=0,F0(r,0,0)=0。

同理,根据圆柱坐标下的二维有限圆柱几何形式[1]给出相应的升阶表达方式:

(18)

式中,z为圆柱高度变量。原函数的定解约束项为:ξ0=-1,F0(r,z,-1,φ)=0;φ0=0,F0(r,z,ξ,0)=0;ξ0=-1,φ0=0,F0(r,z,-1,0)=0。

其他多维几何方程可据此类推,定积分项的处理方法相同。

在式(9)基础上,通过确定原函数表达的升阶后输运方程形式如下:

(19)

4 微分升阶后的方程边界条件表达方法

常见的中子输运方程边界条件包括:中子通量密度为有限非负实数、连续边界条件、自由边界条件、全反射边界条件、反照边界条件等[1-3]。原中子输运方程微分升阶后,由于中子输运方程是由原函数表达的,需参照式(7)、(8)将原函数关于通量密度角度进行求导,变换为F(r,μ)′、Fξ,φ(r,ξ,φ)表示角通量密度函数φ(r,μ)、φ(r,ξ,φ),然后进行原中子输运方程的边界表达,部分边界的形式列于表1。其他形式边界可据此根据边界类型与方程的几何形式类推。

表1 边界表达形式Table 1 Boundary representation

5 深度学习数值计算方法

基于PINN基本网络架构[5,8],结合升阶后中子输运方程原函数特点,进行深度学习方法设计与实现,其原理与流程是:将人工神经网络函数作为原函数F0(r,Ω)的试函数,代入方程中得到的残差形成控制方程损失函数,与边界条件约束、原函数定解约束、特征值约束形成的损失函数,加权后得到统一的损失函数;将神经网络神经元连接权重及有效增殖因数keff作为可以调节的优化参数,以降低加权损失函数为目标进行深度学习;当损失函数趋近于极小值时,神经网络函数趋近于原函数的解。最后,对原函数关于角度变量求导降阶,获得原中子输运方程角通量密度的数值解。

l层神经网络函数形式[15]为:

Nl(x)=fl(wlfl-1(wl-1fl-2(…f1(w1x+

b1)…+bl-2)+bl-1)+bl)

(20)

式中:w为神经网络连接权重;b为神经网络偏置项;Nl(x)为神经网络输出;x为神经网络输入向量;f为激活函数。

将式(20)作为试函数,代入到控制方程、边界条件约束、原函数定解约束、特征值约束中,生成相应的损失函数。

1) 控制方程损失函数

令N(xr,xΩ)=F0(r,Ω),其中神经网络向量xr为方程空间几何变量,xΩ为方程角通量密度角度变量,xr、xΩ可根据r、Ω维度做适应性调整。

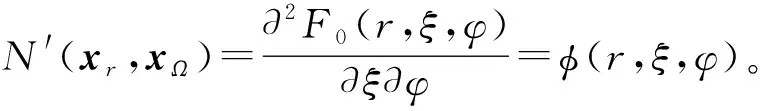
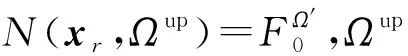
将式(20)及上述等价关系代入式(19),得到控制方程残差表示的方程损失函数为:

(21)

式中,i为机器学习所需要的样本点,可按照一定的概率密度分布生成,或根据方程的形式、边界条件采用不同密度分布策略生成[8]。

2) 边界条件约束损失函数

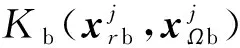
(22)

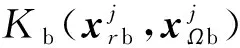
3) 原函数定解约束损失函数

设φ(r,Ω)定义域中,rd,Ωd∈Гd为原函数的定解约束取值域,F0(rd,Ωd)为第3节所示的定解约束函数项,令式(20)为N(xrd,xΩd)=F0(rd,Ωd),则得到原函数定解约束项损失函数为:

(23)

式中,m为定解约束项取值域上的机器学习样本点。

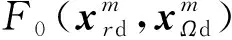
4) 特征值约束损失函数

如文献[1-3]所述,由于稳态中子输运特征值方程相同特征值的解有无穷多个,直接用深度学习方法求解在收敛速度上存在一定困难。解决的方法是通过增加特定固定的几何空间点,设定归一化的通量密度预设值,构建相应的特征值约束损失函数来提高收敛速度[8]。固定的几何空间点一般选择通量密度的对称点、中心点等,预设固定值理论上可以是任意实数值,取值的大小会影响最终通量密度分布的幅度,但不会影响其分布形状。实际应用中,可根据堆芯功率设定等应用需要,类似传统求解输运方程的方法,对最终结果做归一化处理,保证计算结果的唯一性。

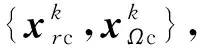
(24)

式中,k为预设值特定样本点。

5) 统一加权损失函数

将上述损失函数加权,得到统一的机器学习损失函数:

Fall-Loss=PfFf-loss+PbFb-loss+

PdFd-loss+PcFc-loss

(25)

式中,Pf、Pb、Pd、Pc分别为控制方程、边界条件约束、原函数定解约束、特征值约束损失函数权重。

深度学习过程是调整式(20)中的wl、bl,若为非临界问题同时调节keff,使得Fall-Loss趋近于0,N(xr,xΩ)趋近于F0(r,Ω)。此后,将N(xr,xΩ)关于角度Ω进行求导降阶,得到的N′(xr,xΩ)即原中子输运方程的角通量密度数值解φ(r,Ω),此时的keff也趋近于系统有效增殖因数的解。实践中一般为Fall-Loss设定一定的收敛准则,机器学习满足收敛准则后停止学习迭代,N′(xr,xΩ)求导采用机器学习自动微分技术实现[16]。

6 数值验证

6.1 临界单群平板几何输运问题

针对式(3)描述的平板几何单群输运问题,设平板材料特性Σt=0.050 cm-1,Σs=0.030 cm-1,νΣf=0.022 5 cm-1,平板两侧为真空边界条件。按文献[2]理论,本题的截面数据相当于C=(Σs+νΣf)/Σt=1.05(C值定义参考文献[2]),根据文献[2]给出的C=1.05时的几何平板临界半厚度,本问题临界半厚度b=3.300 263 772λ=66.005 275 44 cm,其中λ=1/Σt为中子自由程,此时keff=1。利用升阶形式方程(式(14))进行深度机器学习求解。

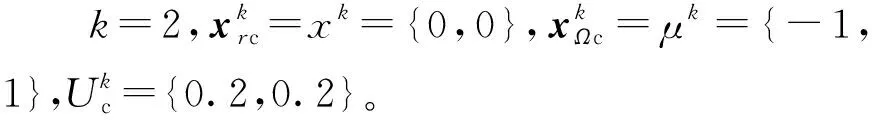
表2 平板几何机器学习损失函数及样本生成方式Table 2 Machine learning loss function and sample generation method of slab geometry

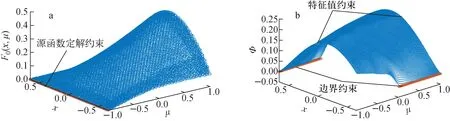
a——升阶原函数分布散点图;b——原函数降阶后的角通量密度分布散点图图1 平板几何单群输运问题数值计算结果Fig.1 Numerical calculation result for single group transport problem of slab geometry

验证实验中,样本数量大一般具有相对较高精度,但学习时间较长,反之样本数量少,学习效率高,但精度下降。为了采用较为少量样本点获得较高的机器学习精度,在控制方程边界附近采用了增加样本点的技术[8],实践中可根据性能要求及硬件环境综合考虑样本数量与方式;同时,权重系数、Pf、Pb、Pd、Pc为经验参数,本文的策略是以Pf=1为基准,在训练初期设定不同的Pb、Pd、Pc,选取使得Fall-Loss下降较快的值进行后续训练。由于神经网络具有一定的不可解释性,对于不同的问题一般有不同的优化值,主要基于实验过程进行选择。

图1示出平板几何单群输运问题数值计算结果,图2示出平板几何下中心归一化定积分项标通量密度散点图。平板几何标通量计算结果与理论值对比列于表3。

如图1、2和表3所示,深度学习技术求解出标通量密度与理论值对比具有良好的精度。同时,由于机器学习获得通量密度分布是通过式(19)形式表达的,而式(19)及其导数形式均为连续函数,通过神经网络的泛化计算可给出角通量密度的连续分布,这相对于SN、MOC等传统方法具有显著的特点。

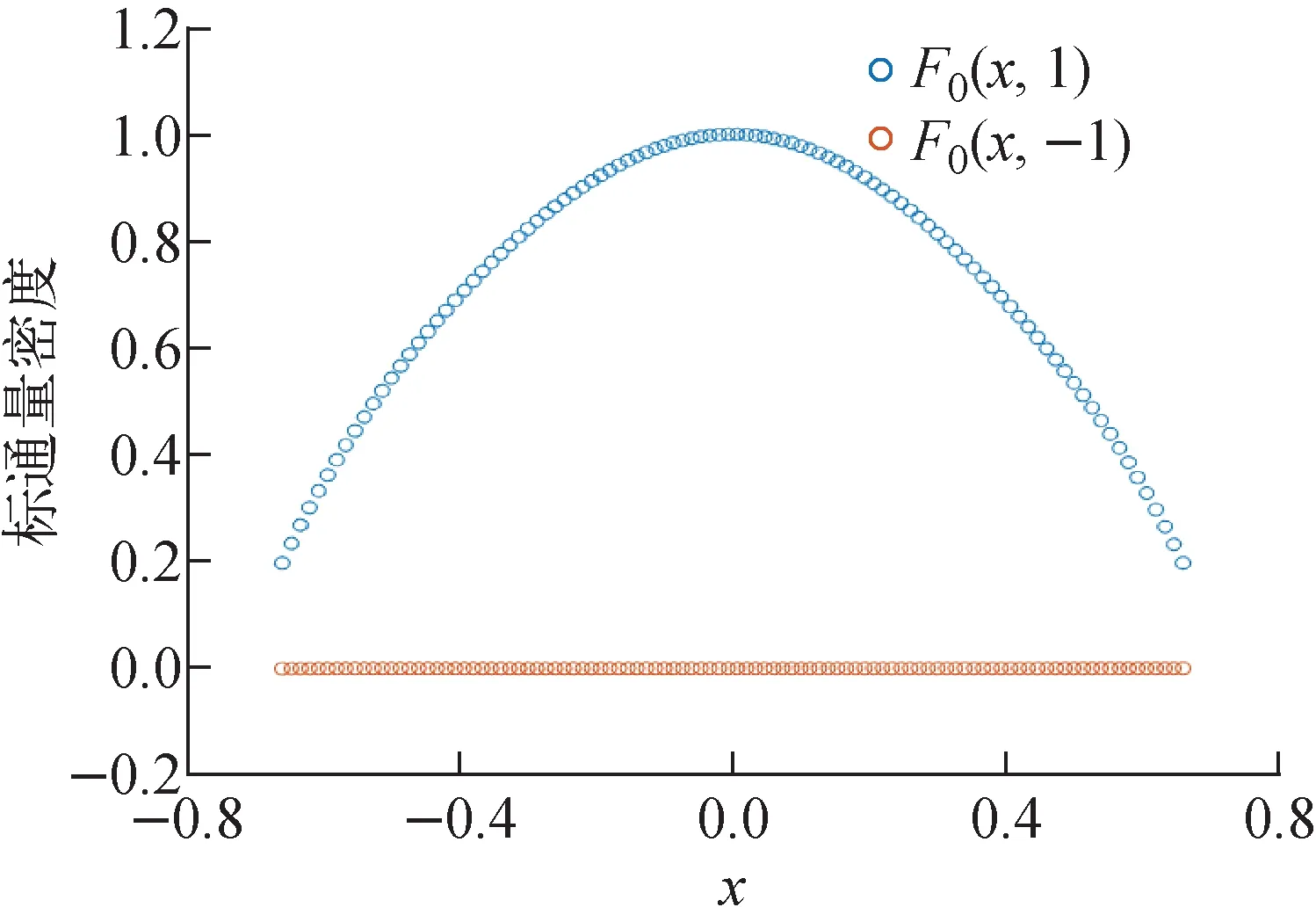
图2 平板几何下中心归一化定积分项标通量密度散点图Fig.2 Scatter plot of normalized definite integral term scalar flux density under slab geometry

6.2 临界单群球几何输运问题

针对式(4)描述的球几何单群单材料区域问题,其材料特性、C与边界条件同6.1节,由文献[2]理论可知C=1.05时的归一化球几何半径R=7.277 181 79λ=145.543 635 8 cm,此时系统为临界时状态,keff=1。利用升阶形式方程(式(15))进行深度机器学习求解。

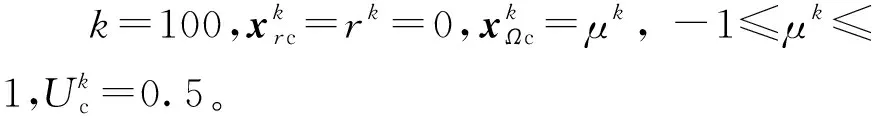
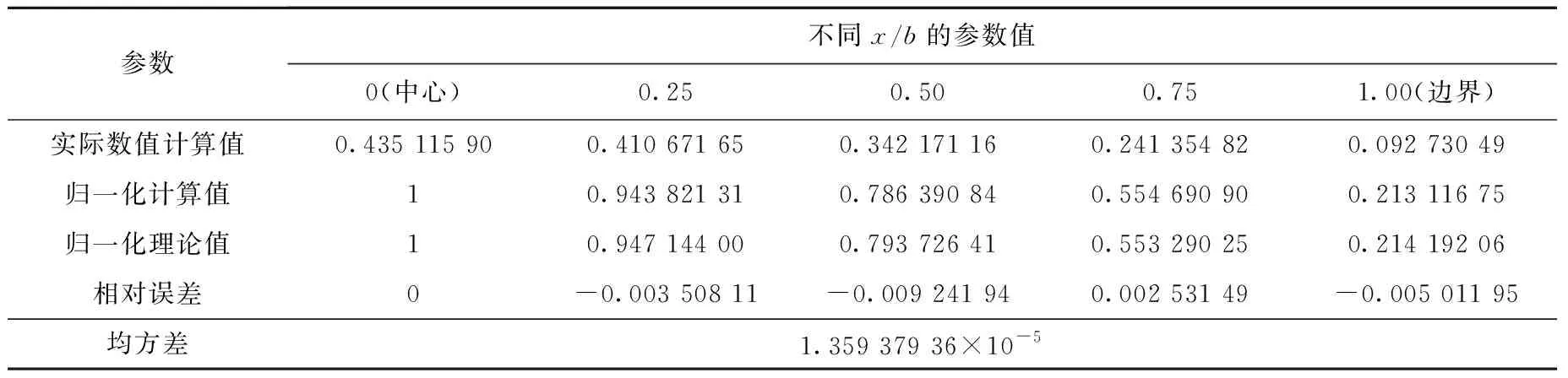
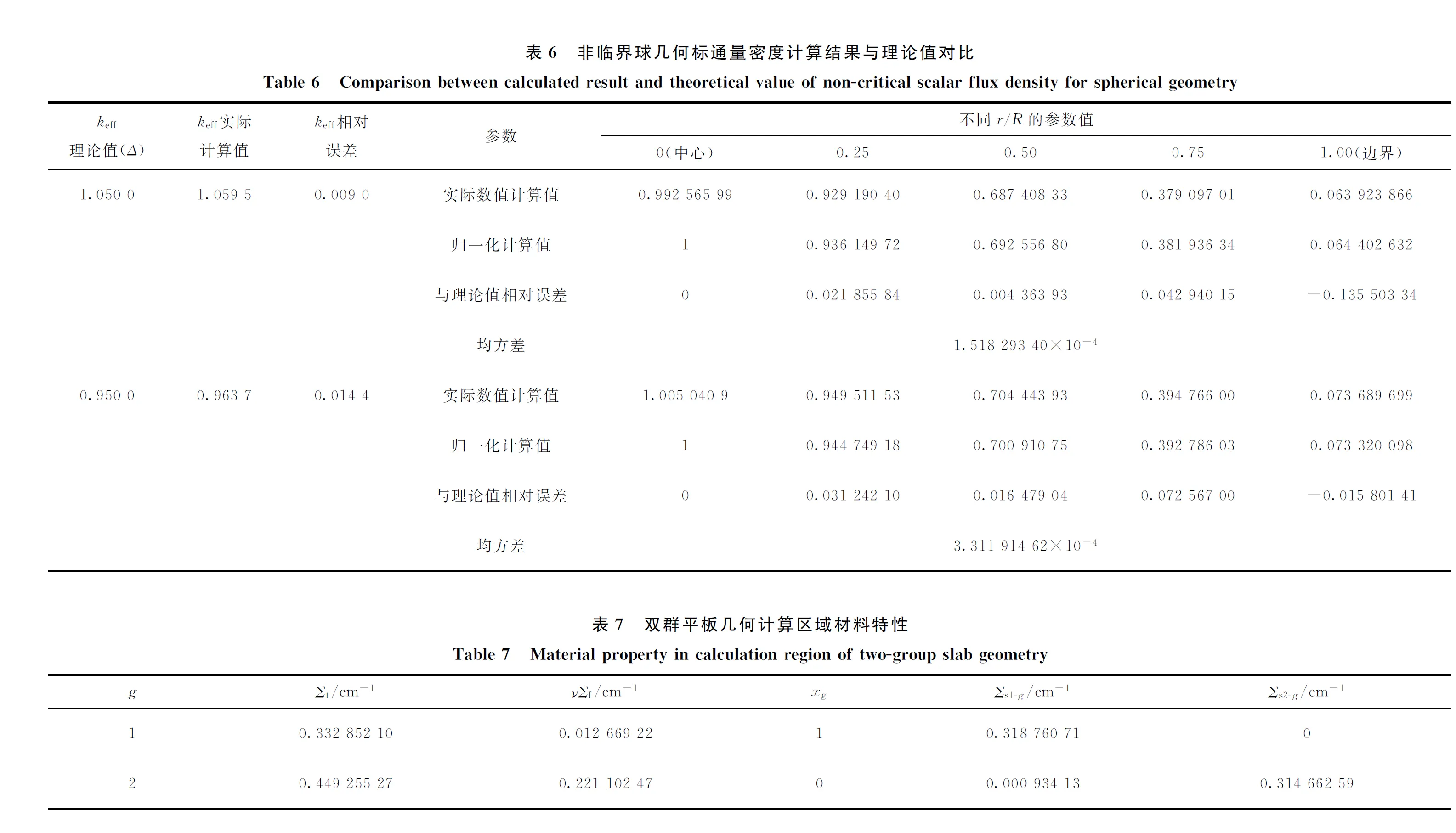
表3 平板几何标通量密度计算结果与理论值对比Table 3 Comparison between calculated result and theoretical value of slab geometric scalar flux density

图3示出球几何单群输运问题数值计算结果。图4示出球几何下中心归一化定积分项标通量密度散点图。临界球几何标通量计算结果与理论值对比列于表5。可见,数值计算结果验证了机器学习方法具有良好的精度,同时也给出了角通量密度的连续分布。

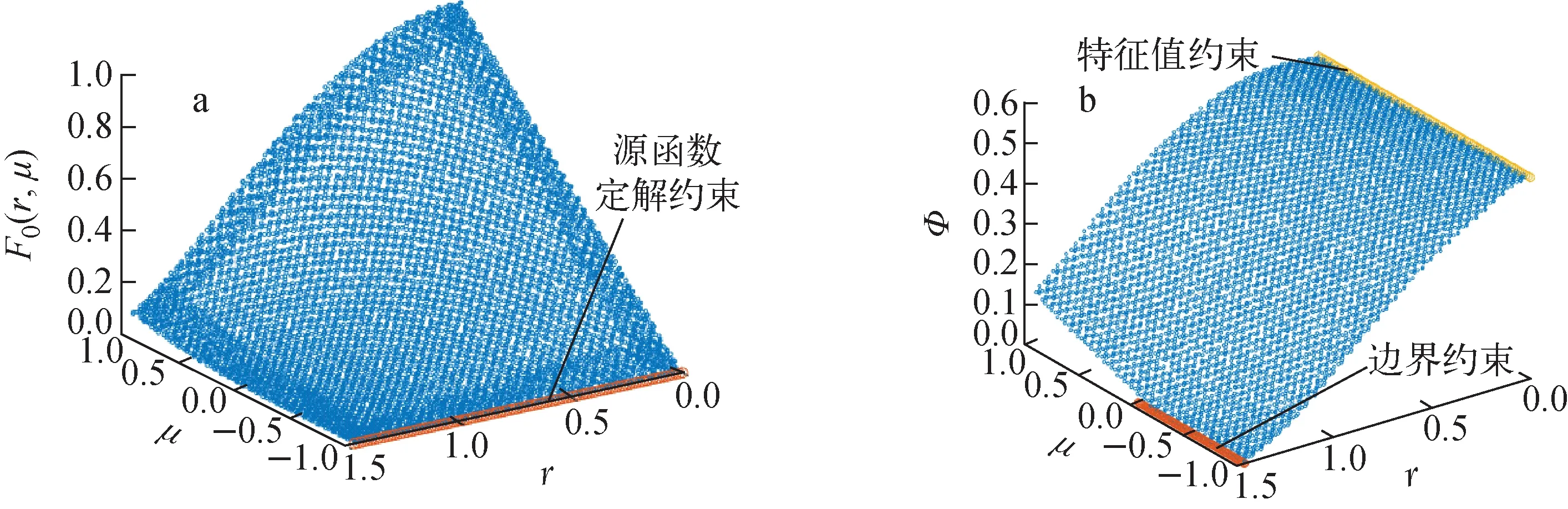
a——升阶原函数分布散点图;b——原函数降阶后的角通量密度分布散点图图3 球几何单群输运问题数值计算结果Fig.3 Numerical calculation result for single group transport problem of spherical geometry

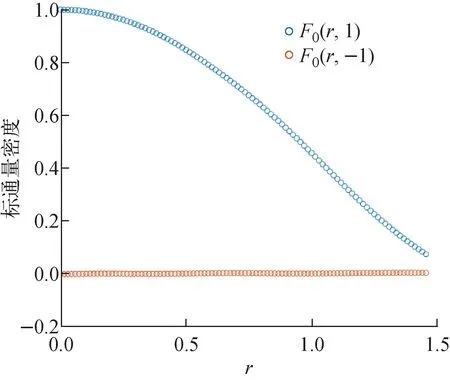
图4 球几何下中心归一化定积分项标通量密度散点图Fig.4 Scatter plot of normalized definite integral term scalar flux density under spherical geometry

6.3 非临界单群球几何输运问题

针对6.2节中球几何单群单材料区域问题,将式(4)中的Σf引入误差Δ,使得Σ′f=Σf·Δ,此时反应堆为非临界系统。当keff=Δ时式(4)成立,将此作为数值计算参考标准理论值,表5中的归一化理论值仍然适用。机器学习方法中交替更新神经网络权重与keff,其余网络参数、损失函数及样本生成方式同6.2节。

非临界球几何标通量密度计算结果与理论值对比列于表6,其升阶原函数与降阶后的通量密度形状与图3、4相似。

本示例可作为评估深度学习求解非临界系统keff误差的标定方法。

6.4 非临界双群平板几何输运问题

针对平板几何双群单材料区域问题,双群平板理论及输运方程形式参考文献[1-3],定积分项处理方法如式(14),几何参数同6.1节,材料参数列于表7。

表5 临界球几何标通量密度计算结果与理论值对比Table 5 Comparison between calculated result and theoretical value of critical scalar flux density for spherical geometry

机器学习方法与参数选择为:用两个神经网络分别表示热群与快群,机器学习过程中,交替更新两个神经网络权重、keff。特征值约束针对快群为:F′0(0, - 1) =F′0(0,1)=0.1,不加入热群特征值约束,即热群Pc=0,其余网络参数、损失函数及样本生成方式同6.1节,keff更新方法同6.3节。

由于此问题本身没有解析解或理论估计值,将深度学习结果与输运计算程序OpenMC[17]获得的标通量密度计算结果进行比较(均以快群的x=0处标通量密度进行归一化),结果如图5、表8所示。由图5可见,数值计算结果也可获得双群系统连续性角通量密度分布。

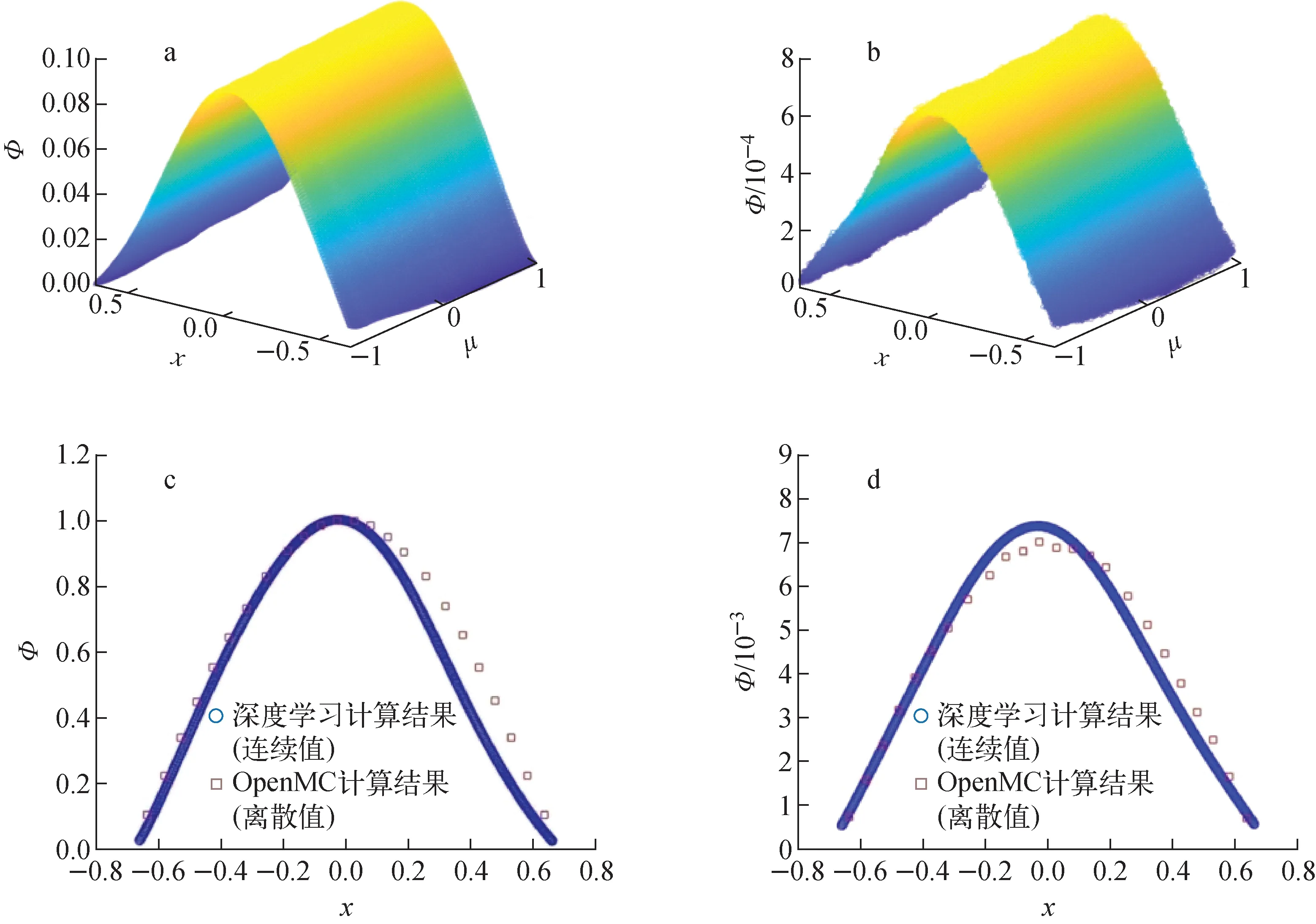
a——快群通量密度计算结果;b——热群通量密度计算结果;c——快群标通量密度与OpenMC软件对比图;d——热群标通量密度与OpenMC软件对比图图5 非临界双群平板几何输运问题数值计算结果Fig.5 Numerical result of transport problem of non-critical two-group slab geometry

表8 非临界双群平板几何标通量密度计算结果Table 8 Calculation result for non-critical two-group scalar flux density of slab geometry

6.5 非临界单群多材料区域平板几何输运问题

非临界单群多材料区域平板几何如图6所示。

平板几何由两种材料3个区域组成,b定义与6.1节相同,材料参数列于表9。

机器学习方法、网络参数、损失函数及样本生成方式同6.1节,keff更新方法同6.3节。将计算结果与OpenMC[17]结果进行比较(按照x=0处的标通量密度进行归一化处理),结果如图7、表10所示。

与前述例题类似,图7a显示出角通量密度连续分布的特点。对照单材料临界系统(图2),机器学习结果(图7b)的标通量密度分布两侧存在明显的“内陷”,与OpenMC结果呈现出的形状相比具有良好的一致性。

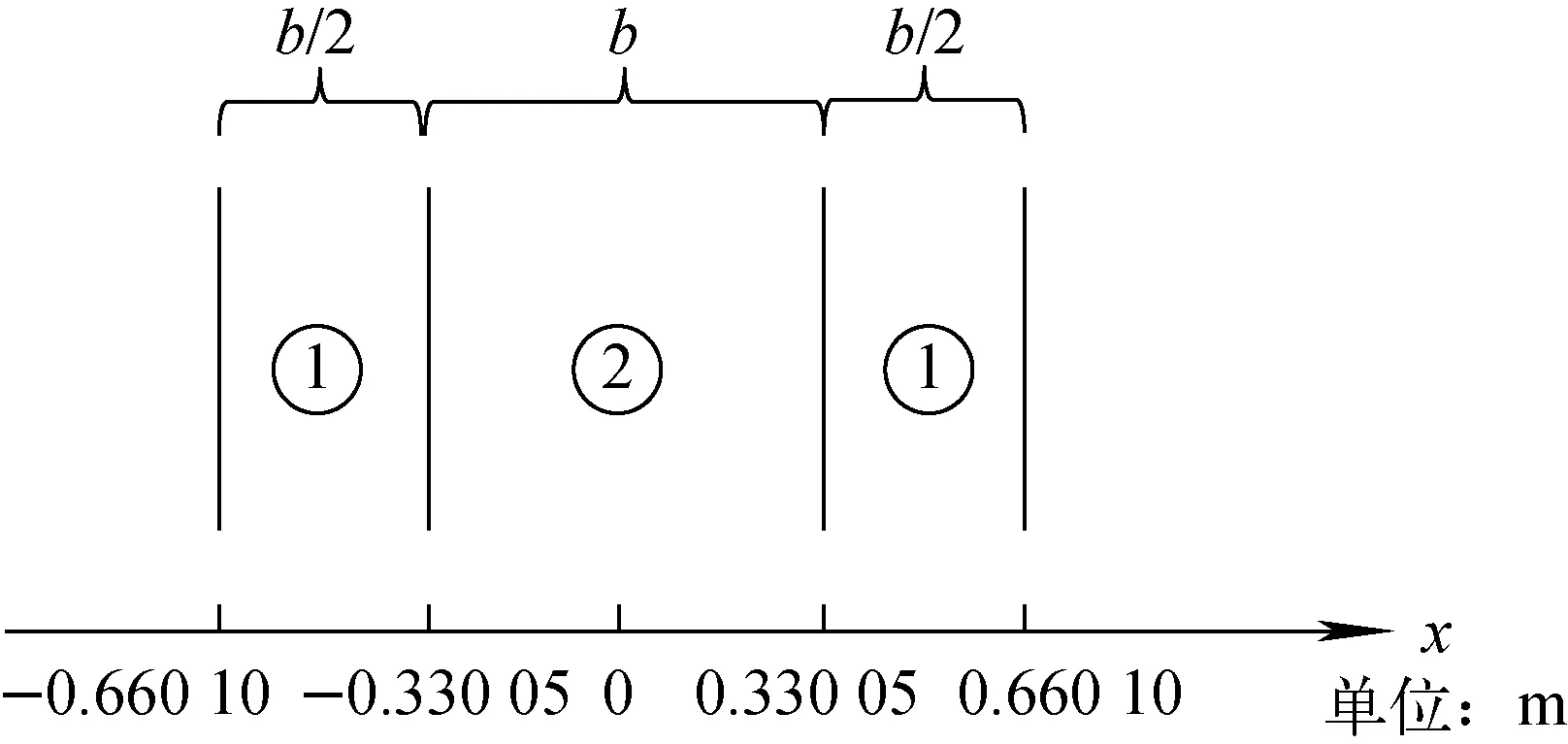
图6 非临界单群多材料问题几何描述Fig.6 Geometric diagram for non-critical single group multi-material problem

表9 非临界单群多材料区域平板几何区域材料特性Table 9 Material property of non-critical single group multi-material region of slab geometry

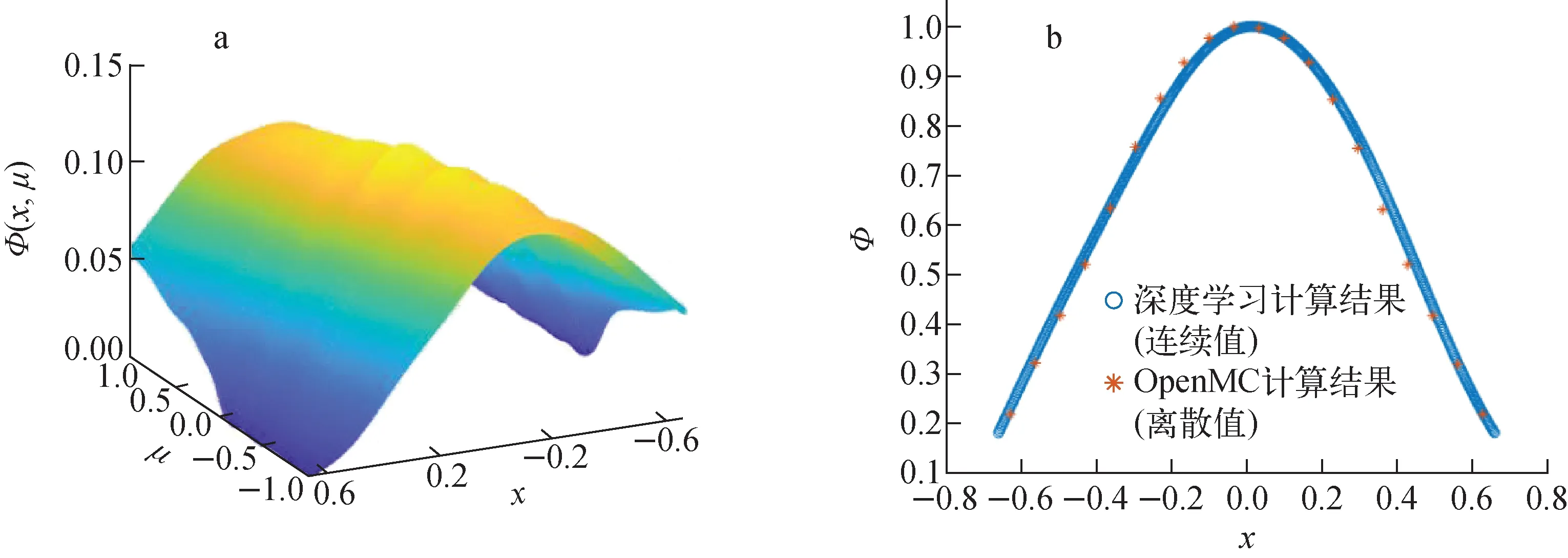
a——角通量密度计算结果;b——标通量密度计算结果与OpenMC结果对比图图7 非临界单群多材料区域平板标通量密度数值计算结果Fig.7 Numerical calculation result of non-critical single group multi-material region scalar flux density for slab geometry

表10 非临界单群平板几何标通量密度计算结果Table 10 Calculation result of non-critical single group scalar flux density of slab geometry

综上所述,上述验证表明微分升阶理论数理方法基本原理在临界与非临界系统下均具有良好的适用性。由于非临界系统keff计算值存在一定误差,尽管这种误差范围与PINN基础框架[5]中的示例相当,但这是导致非临界系统的角通量密度精度低于临界系统的重要因素。

7 结论

本文针对当前深度学习技术求解微分方程的方法不能直接适用于具有积分项的中子输运方程面临的困难,提出了将输运方程通过数理方法升阶为高阶微分形式的原函数进行机器学习,成功后再将其降阶为原方程数值解的微分变阶理论。同时,给出了相应的原函数定解条件约束、边界条件约束、特征值约束形式等损失函数构造方法。最后,分别通过临界与非临界平板、球几何例题,验证了该理论及相关方法的正确性。研究表明机器学习方法求解得到数值结果具有几何-角通量密度分布连续性的特点。研究工作为中子输运方程的数值求解方法探索出了新的技术途径,并为利用深度学习方法求解几何、能群更加复杂的中子输运方程提供了良好的技术支撑。