解两类含参数的复合不等式有解与恒成立问题
江西省贵溪市第四中学(335400) 吴善祥
1 问题呈现
笔者在高三的一堂课上,讲解了下面一道题.
题目关于x的不等式x2−2ax>4 −a2在区间[0,1]内恒成立,求实数a的取值范围.
笔者提供的解法如下:
解(x−a)2−4 > 0,令f(x) = (x−a)2−4,由题意知f(x) > 0 在区间[0,1]内恒成立,所以或即或解得a< −2 或a> 3, 因此实数a的取值范围为(−∞,−2)∪(3,+∞).
但课堂上有一个学生举手示意他有另一种解法,想拿出来分享. 该学生的解法如下:
解x2−2ax> 4 −a2⇔(x−a)2> 4⇔a
这位学生分享完他的解答之后,便向大家抛出了他那双期待点赞的眼神.
笔者没有着急给出评价, 只是问该学生从“a
问题“a
2 问题探究
下面, 就来探讨一下“a
“a
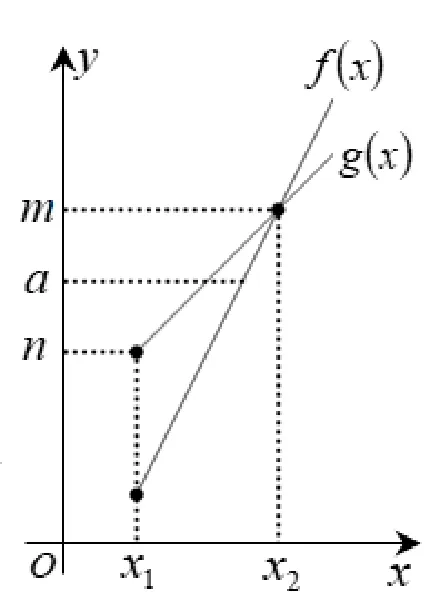
图1
“g(x)≤a≤f(x)在区间D内有解”又如何解决呢? 是否直接等价于“g(x)min≤a≤f(x)max”呢? 下面做进一步的探究.
首先, 在区间D内g(x)min和f(x)max都不一定存在,所以“g(x) ≤a≤f(x) 在区间D内有解”直接等价于“g(x)min≤a≤f(x)max”是不严谨的. 其次, 就算在区间D内g(x)min和f(x)max存在,“g(x) ≤a≤f(x) 在区间D内有解”也不一定等价于“g(x)min≤a≤f(x)max”.如图2, 在区间[x1,x3] 内,f(x)max=m,g(x)min=n. 当p 图2 g(x) ≤a≤f(x) 在区间D内有解, 务必确保f(x) ≥g(x),由f(x) ≥g(x)在区间D内解出一个区间C,在区间C求g(x)的最小值g(x)min和f(x)的最大值f(x)max. 否则,x的取值区间有可能就被放大了,从而导致g(x)的最小值可能被缩小,f(x)的最大值可能被放大. 通过上面的研究,便得到解决“g(x) ≤a≤f(x)在区间D内有解”这类题型的一般步骤如下: 第一步,控制区间: 在区间D内解不等式f(x) ≥g(x),设其解集为C; 第二步,求出最值: 在区间C内,如果g(x)存在最小值,f(x)存在最大值,那么求g(x)的最小值g(x)min和f(x)的最大值f(x)max; 第三步,得出结论:g(x)min≤a≤f(x)max. 对于f(x)和g(x)在区间内最值不存在的情况,一般可以考虑趋向于某个常数或者无穷大来处理此类问题. 后文碰到此类情况,类似处理,不再赘述. 现在回到前面的题目,便可以得到此题的另一种正确解法: 解法2x2−2ax>4−a2⇔(x−a)2>4⇔a 上面在由条件f(x) ≥g(x)控制的区间C内去求g(x)的最小值和f(x)的最大值,其实都是在区间C是连续区间的情况下探讨的. 如果区间C是多个连续小区间的并集,那么只要在每个小区间上分别去求参数a的取值范围,最后将它们取并集即为所求. 直到现在, 估计大家还有一个疑问, 既然“a 此时,再来一题,看计算的结果是否一样. 例1若a<6x−2 或a>x+2 在x∈[0,1]内恒成立,则实数a的取值范围是____. 错解因为a< 6x−2 或a>x+ 2 在x∈[0,1]内恒成立, 所以a< 6x−2 区间x∈[0,1] 内恒成立或a>x+2 区间x∈[0,1]内恒成立,所以a< (6x−2)min=−2 或a> (x+2)max= 3, 因此实数a的取值范围为(−∞,−2)∪(3,+∞). 上面已经探讨了“a 类似于解决“g(x) ≤a≤f(x)在区间D内有解”问题,很多学生容易得出“g(x) ≤a≤f(x)在区间D内恒成立”的解题步骤: 第一步,控制区间: 在区间D内解不等式f(x) ≥g(x),设其解集为C; 第二步,求出最值: 在区间C内,如果g(x)存在最大值,f(x)存在最小值,那么求g(x)的最大值g(x)max和f(x)的最小值f(x)min; 第三步,得出结论:g(x)max≤a≤f(x)min. 从正确与否的角度来看, 这种解题步骤是没有问题的. 但从解题步骤的简洁性来说, 这种解题步骤还有待简化. “g(x) ≤a≤f(x) 在区间D内恒成立”已经确保了“f(x) ≥g(x) 在区间D内恒成立”. 所以, 第一步在区间D内不等式f(x) ≥g(x) 的解集C毫无疑问就等于D. 因此,在区间D内,若f(x)存在最小值,g(x)存在最大值, 则“g(x) ≤a≤f(x) 在区间D内恒成立”直接等价于“g(x)max≤a≤f(x)min”,无需由f(x) ≥g(x)在区间D内重新控制一个约束区间,给计算带来没有必要的麻烦. 例2若关于x的不等式|a−3x−1| ≤2x2在区间[1,2]内恒成立,则实数a的取值范围是____. 解|a−3x−1| ≤2x2⇔−2x2+ 3x+ 1 ≤a≤2x2+ 3x+ 1. 在区间[1,2] 内,(−2x2+3x+1)max= 2,(2x2+3x+1)min=6. 因此a的取值范围是[2,6].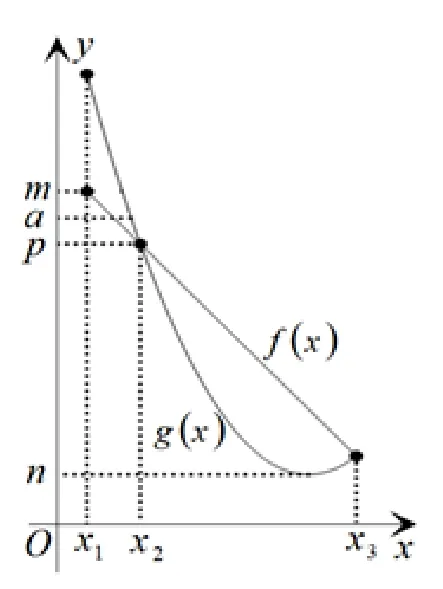
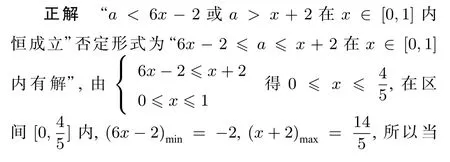

3 拓展延伸
3.1 g(x)≤a≤f(x)在区间D内恒成立
3.2 a≤g(x)或a≥f(x)在区间D内有解


