基于递推最小二乘法的分合闸线圈参数辨识与在线监测

黄堤彬

（厦门斯玛特思智能电气有限公司，福建 厦门 361000）

高压断路器是电力系统中十分重要的电气设备，主要用于控制负荷电流的关合和开断，同时当电力系统出现短路故障时能够及时切断故障电流，起到控制负荷和保护电力设备的双重作用。因此，研究如何提高高压断路器的可靠性对于提高整个供电系统的可靠性有着积极的作用[1-3]。

高压断路器的可靠性很大程度取决于断路器操作机构的可靠性，因此断路器的机械故障诊断对于提高断路器的可靠性意义重大[4]。

断路器的机械故障主要有分合闸线圈故障、弹操机构故障、触头磨损、油缓冲器故障等。分合闸线圈是断路器分闸操作和合闸操作的触发元件，保证分合闸线圈的可靠性是保证整个断路器可靠性的基础。若分合闸线圈出现卡滞或者内部短路，极有可能造成断路器拒动，从而产生灾难性的后果。因此在断路器健康状态在线监测中，合分闸线圈的在线监测是其主要监测内容之一。

分合闸线圈故障主要有线圈卡滞、线圈内部匝间短路和线圈开路等[5-6]。本文从分合闸线圈的电感和电阻辨识的角度出发，研究使用带遗忘因子的递推最小二乘法对分合闸线圈的电感和电阻进行在线辨识。若分合闸线圈内部出现匝间短路故障，则其辨识得到的电感和电阻必然会出现较大的变化，通过这个变化可以识别出线圈内部短路故障。

1 分合闸线圈的静态特性分析

1.1 运动过程分析

分合闸线圈得电之后，动铁芯内部会产生磁通从而产生电磁力，此时动铁芯依然处于静止状态，线圈的磁链、电流以及铁芯受到的电磁力急剧上升。当电磁力大于复位弹簧阻力和内部摩檫力之后，动铁芯开始运动。从线圈得电到铁芯开始运动的过程称为触动过程[7]。铁芯经过电磁力进行加速之后最终撞击合闸或者分闸操作机构，触发操作机构释放弹簧力，从而实现高压断路器的分闸和合闸操作。

分合闸线圈动作的过程中的电流波形如图1所示。

图1 分合闸线圈电流波形示意图

图1 中的ab段表示的是线圈的触动过程。从b点开始，铁芯开始加速运动，此时电感值随着铁芯的运动开始增加。电流的增长趋势随着铁芯运动而减少，直到电流达到c点，电流加速度等于0。然后铁芯继续加速运动，电感值急剧上升，电流急剧下降，直到到达d点，铁芯触碰到分合闸操作机构，受到分合闸操作机构的阻力。在d点由于铁芯受到了机械阻力，所以de段电流会出现短暂的上升，然后铁芯继续向前加速电流下降，直到到达e点之后铁芯由于限位停止运动。

整个运动过程大致可以分成3 段：触动过程ab、运动过程be、停止过程ef。其中触动过程和停止过程属于静态过程，其分析较为简单。运动由于受铁芯速度、位移以及受力情况的影响，其过程较为复杂。本文主要研究分合闸线圈的触动过程。

1.2 模型分析

分合闸线圈触动过程的等效电路模型如图2 所示[6]。

图2 分合闸线圈等效电路图

根据等效电路，可以得到以下关系式：

式（2）中：L（x，i）为线圈的电感，它是关于铁芯运动距离x和电流i的非线性函数。

通过对式（2）进行求导，可得：

本文研究的是分合闸线圈的触动过程的参数辨识，此时距离x

=0，因此可以省略铁芯运动的影响。由于微分电感受电流变化的影响不是十分明显，为了计算方便，故式（3）中电感对于电流的二次求偏导可以省略[8]。且在触动过程中电感L（x，i）为常量，与电流和运动距离无关，电感L（x，i）可以直接用L表示。因此式（3）可简化为：

将式（4）代入式（1）可得：

对式（5）进行离散化可得：

式（7）中：Ts为采用间隔，s；ik-1为第k－1 次的电流测量值，A；uk－1为第k－1 次的电压测量值，V。

1.3 带遗忘因子的递推最小二乘参数辨识方法

递推最小二乘法（Recursive Least Squares，RLS）由于原理简明、收敛较快、易于理解、易于编程实现等优点，被广泛应用于定常未知参数系统的辨识应用中[9]。实际工程应用中有一些应用场景要考虑的是参数时变系统，其中包括2 种情况：参数突变但不频繁和参数缓慢变化。在递推最小二乘法的基础上，引入遗忘因子，诞生了适用于参数时变系统的带遗忘因子的递推最小二乘法（Forgetting Factor Recursive Least Square，FFRLS）[10]。

待辨识系统的输入-输出模型可表示为：

写成向量的形式，可以表示如下：

式（8）（9）中：yk为系统输出量的第k次观测值；θ为待辨识的参数向量；ek为系统的测量噪声；φk为输入-输出观测向量。

将式（7）代入式（9）可得式（10）：

对于公式（9）所示的待辨识的系统模型，其带遗忘因子的递推最小二乘辨识公式如下[6]：

式（11）中：λ为遗忘因子，通常情况下0.95≤λ≤1。

2 仿真分析

2.1 仿真模型搭建

在Simulink 中搭建如图3 所示的仿真模型，模拟分合闸线圈触动过程的电流变化，同时在测量得到的电压和电流信号中引入白噪声信号，模拟实际应用中存在的测量噪声。选取直流220 V 电源作为操作电源，模拟线圈电感为0.275 H，线圈内阻为138 Ω，离散步长20.83 μs，对应采样率48 kHz。

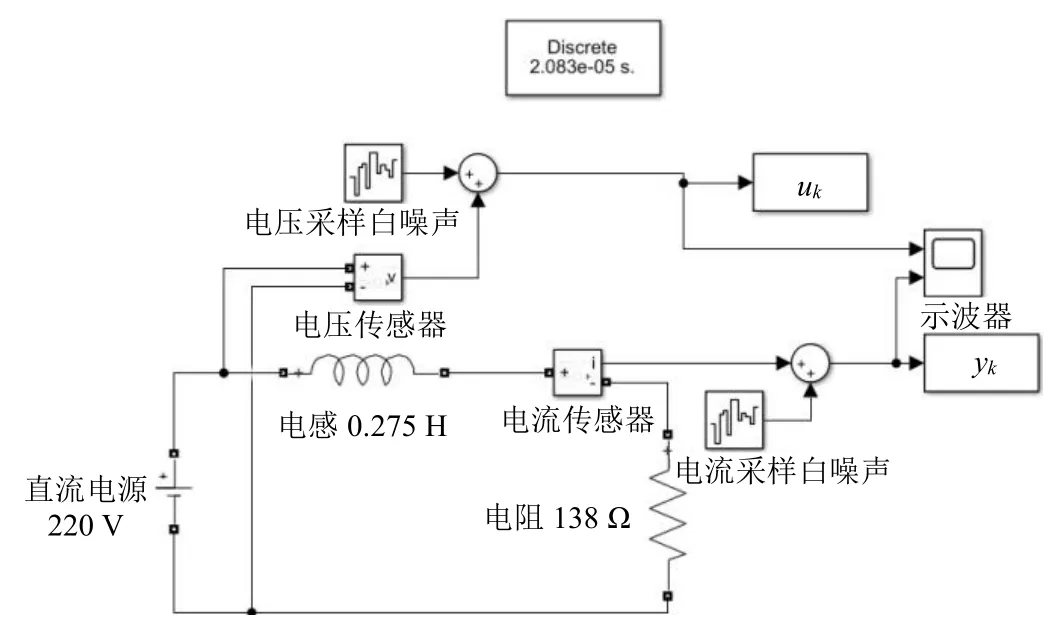
图3 仿真模型

2.2 仿真结果

通过上述的仿真得到模拟线圈触动过程的输入uk和输出参数yk，如图4 和图5 所示。使用公式（11）所示的FFRLS 算法对其进行参数辨识，取遗忘因子为0.98，得到如图6 和图7 所示的结果。从结果中可见FFRLS 算法得到的a1和b0在k大于40 以后就迅速地收敛。

图4 仿真模型系统输入参数uk

图5 仿真模型系统输出参数yk

图6 仿真模型系统辨识输出a1

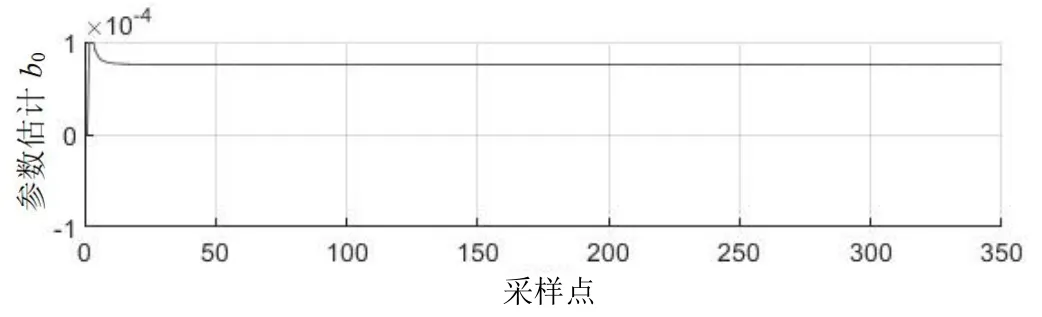
图7 仿真模型系统辨识输出b0

通过公式（10）中对应关系，可以得到电感L和电阻R与辨识得到的a1和b0的关系式如下：

使用上述公式对电感L和电阻R进行求解，得到最终的L和R的辨识曲线如图8、图9 所示。

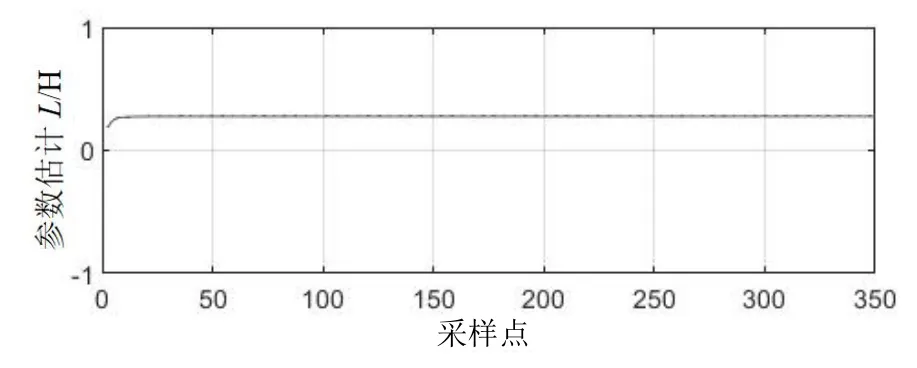
图8 求解的电感L 结果

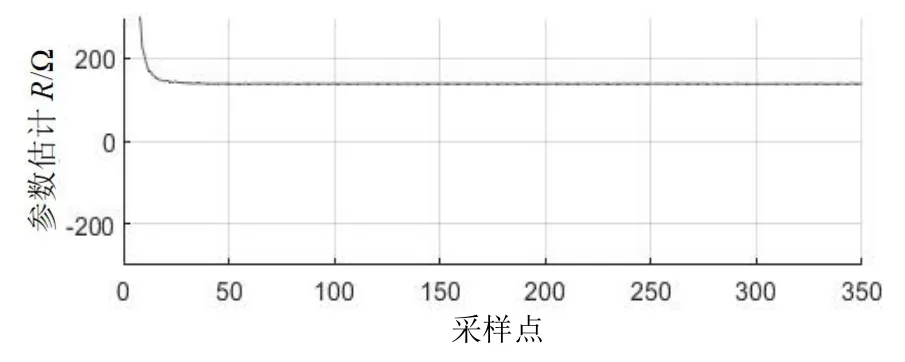
图9 求解的电阻R 结果

在图8、图9 中可见，求解得到的L和R在k大于40 之后就基本上达到稳态，最终稳定在L=0.276 4 H，R=138 Ω，与仿真设置的电感和电阻参数一致。

通过上述的仿真分析，说明使用FFRLS 算法能够快速对线圈的触动过程的线圈电感和电阻进行辨识。一般而言，辨识参数的收敛速度取决于遗忘因子的选择，遗忘因子越大，收敛的速度越慢，辨识的结果方差越小。遗忘因子越小，其收敛的速度越快，辨识的结果方差越大，数据抖动较大。

3 实验验证

3.1 实验平台搭建

将仿真验证通过的FFRLS 算法移植到厦门斯玛特思智能电气有限公司SED-560 系列在线监测装置，该装置选用STM32F407ZGT6 作为主控制器，其主频达到168 MHz，带硬件浮点计算功能。AD 芯片选用AD7606，16 位高精度采样，内部自带抗混叠滤波器。选用CHCS-GB5-10 A 霍尔电流传感器采集分合闸线圈电流、选用CHVS-AS5-05 mA 霍尔电压传感器采集分合闸操作电压。

以某公司的VS1 断路器为实验对象，其分合闸线圈规格为220 V，内阻130 Ω。实验平台如图10 所示。

图10 实验环境

图10 中SED-560 装置接入2 个霍尔电流传感器采集分合闸线圈电流，一个霍尔电压传感器采集操作电压。当断路器进行电动分合闸操作时，装置通过霍尔电流传感器检测到线圈电流突变，启动电压、电流进行录波。当断路器操作完成之后，检测到线圈电流返回，停止录波。将记录到的波形进行FFRLS 参数辨识，最后将辨识结果和原始波形存储到装置的文件系统，录波采用COMTRADE 格式进行存储。

3.2 实验验证

首先验证同一个操作电压下，连续动作多次的实验结果，用于验证该算法在实际应用中的稳定性，其结果如图11、图12、表1 所示。

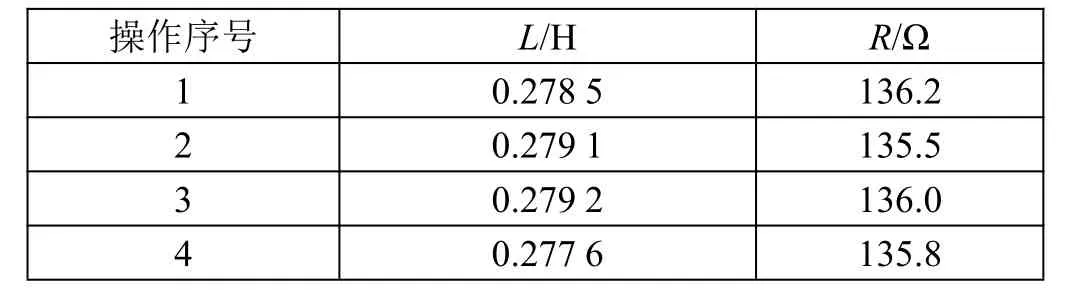
表1 统一操作电压下多次辨识的结果记录表

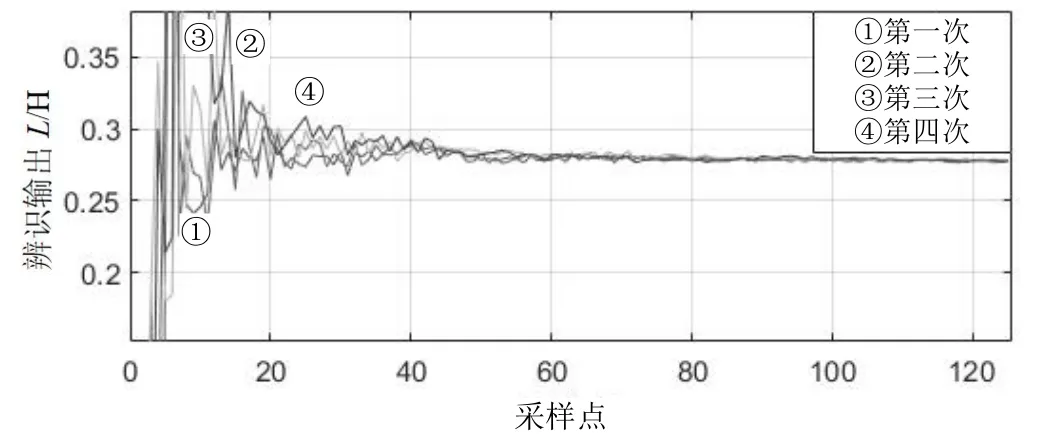
图11 同一操作电压下动作多次辨识的电感结果

图12 同一操作电压下动作多次辨识的电阻结果

实验结果表明，在固定的操作电压下，使用FFRLS算法能够稳定地辨识出分合闸线圈触动过程中的电感和电阻。然后验证在不同操作电压下使用FFRLS 算法进行系统参数辨识的适应性。实验结果如图13、图14、表2 所示。

表2 不同操作电压下辨识的结果记录表

图13 不同操作电压下辨识的电感结果

图14 不同操作电压下辨识的电阻结果

实验结果表明，在不同的操作电压下，使用FFRLS算法能够稳定地标识出分合闸线圈触动过程中的电感和电阻，且具有较高的辨识精度。

4 结论

本文首先分析了高压开关分合闸线圈的运动过程及等效电路并对其微分方程进行简化和离散化。然后对FFRLS 算法进行分析，通过搭建Simulink 仿真模型，验证了FFRLS 算法对分合闸线圈的触动过程的电感和电阻进行辨识的可行性。最后通过将FFRLS 算法移植到实际在线监测的产品，验证了FFRLS 算法的有效性和稳定性。实验结果表明，FFRLS 算法能够有效辨识分合闸线圈触动过程中的电感和电阻，且具有较高的辨识精度。该方法能够为分合闸线圈在线监测提供有效的算法支持，为判别线圈匝间短路故障提供可靠的判别方法。