优先级k-中心问题的FPT近似算法

冯启龙，龙睿，吴小良，仲文明

(1. 中南大学 计算机学院，湖南 长沙，410083；2. 湘江实验室，湖南 长沙，410205；3. 中南大学 外国语学院，湖南 长沙，410083)

当今社会已进入信息化时代。研究人员通过数据挖掘技术从海量数据中获取信息资源，其中，聚类算法是数据挖掘的主要技术之一，其作用是将海量数据集划分为多个类簇，使同一类簇中数据点相似性尽可能大，不在同一类簇中的数据点差异性尽可能大[1]，即相似数据尽量聚集，差异数据尽量分离。聚类算法在生物学[2]、文本分类[3]、商业分析[4]、设施选址[5]和隐私保护[6]等方面都有着广泛应用。常见的聚类问题包括k-平均问题[7]、k-中心问题[8-9]、k-中值问题[10]、k-设施选址问题[11-13]、容错设施选址问题[14-16]、带容量的设施选址问题[17-19]、不带容量的设施选址问题[20-22]和优先级k-中心问题[23-30]等。本文对优先级k-中心问题进行研究，该问题是k-中心问题的一种变形问题。给定度量空间中1 个大小为n的集合X和1 个正整数k∈N+。k-中心问题目标是求解1 个大小为k的子集S⊆X，使得集合X中所有的点到其最近中心点的最大距离最小。假设集合X是由n个城市组成的集合，在实际生活中，人们希望所在城市离服务中心越近越好，以此来降低日常的生活开销。PLESNIK 等[23]通过赋予集合X中的每个点权重，提出了带权重的k-中心问题。GORTZ等[24]将带权重的k-中心问题命名为优先级k-中心问题。优先级k-中心问题是NP难问题[23]，不存在多项式时间求解的算法，因此，研究人员大多考虑使用近似算法求解优先级k-中心问题。虽然近似算法得到的可行解不是最优的，其与最优解之间存在一定误差，但可以保证误差在一定范围内。近似比是衡量近似解和最优解之间差距的指标，其值越小表示算法求出的近似解与最优解越接近，算法效果越好。因此，近似算法的设计目标是给出尽可能小的近似比。目前，对于优先级k-中心问题，GORTZ等[24]给出了近似比为2的近似算法，并且2-近似也是该问题的近似下界[9]。固定参数可解(fixed-parameter tractability, FPT)的近似算法采用参数计算方法寻求问题的近似解，是实际中处理NP-难问题的一种新的有效手段。因此，本文考虑优先级k-中心问题FPT时间内的近似算法，给出1个FPT时间内的(1+ϵ)-近似算法，其中ϵ(ϵ＞0)是用于控制算法近似比的参数。本文提出的算法是在时间复杂度和近似比之间寻找折中方案。当ϵ趋近于0时，算法给出的近似解将无限接近于最优解。当ϵ越大时，算法时间复杂度越小。在近似比方面，相比于2-近似算法，本文给出的算法近似比更低。

1 问题定义

本节主要给出相关问题的定义。

定义1(度量空间)：度量空间是1 个有序对(M，d)，其 中M是1 个 点 集，d为1 个 映 射M×M→R+。对于任意a，b，c∈M，映射d满足以下3个 性 质：1) 如 果d(a，b) =0 当 且 仅 当a=b；2)d(a，b) =d(b，a)；3)d(a，b) +d(b，c) ≥d(a，c)。

给定度量空间(M，d)中的1 个集合X，对任意半径R＞0 和点v∈X，令Ball(v，R) ={x∈X∣d(v，s)≤R}，表示以点v为中心、R为半径的集合。对任意点v∈X和集合S⊆X，令d(v，s)表示点v到集合S的距离，其中，d(v，s)=mins∈Sd(v，s)。

定义2(k-中心问题)：给定度量空间(M，d)中的1 个集合X和正整数k∈N+，目标是求解1 个大小为k的集合S⊆X，使得集合X中所有的点到其最近中心点的最大距离最小，即最小化目标函数maxv∈Xd(v，S)。

记(X，d，k)为k-中心问题的1 个实例。给定集合X的1 个子集S，令C(S) =maxv∈Xd(v，S)表示S关于X的代价。

定义3(优先级k-中心问题)：给定度量空间(M，d)中的1 个集合X和正整数k∈N+，其中集合X中的每个点v被赋予1个优先级参数r(v) ∈R+，求解1个大小为k的集合S⊆X，考虑集合X中任意数据点到集合S的距离与r(v)之间比值，找到最大比值，目标是最小化该比值，即使目标函数maxv∈Xd(v，S)/r(v)最小化。

记(X，d，k，r)为优先级k-中心问题的1 个实例。当优先级参数r(v)都相同时，优先级k-中心问题变为k-中心问题。

定义4(加倍度量维度)：给定度量空间(M，d)中的1 个集合X，若对任意点v∈X和半径R＞0，以点v为中心、R为半径的集合Ball(v，R)可以被数量小于等于D个半径为r/2 的集合覆盖，则称D为集合X的加倍度量维度。

2 研究现状

k- 中心问题是NP难问题[8]， 目前，HOCHBAUM 等[8]提出了k-中心问题近似比为2 的近似算法，并且所得到的近似比是k-中心问题当前最好的结果。PLESNIK[23]提出了带权重的k-中心问题，基于k-中心问题中的贪心算法，给出了1个多项式时间内的2-近似算法。因为k-中心问题的近似下界是2，所以，带权重的k-中心问题的近似下界也是2。GORTZ等[24]将带权重的k-中心问题命名为优先级k-中心问题。

此后，研究人员开始对带其他约束条件的优先级k-中心问题或相关的优先级问题如带噪声的优先级k-中心问题[25,29]、优先级k-均值问题[26-28]、优先级k-中值问题[26-28]和优先级k-供应商问题[29-30]等进行了研究，并提出了许多近似算法以解决这些问题。针对带噪声的优先级k-中心问题，HARRIS等[25,29]基于线性规划和最小费用流技术提出了1个多项式时间内的9-近似算法。针对优先级k-均值问题和优先级k-中值问题，NEGAHBANI等[26]基于线性规划方法，在放松优先级约束条件下，给出了近似比为8的算法。VAKILIAN等[27]考虑了优先级k-中值问题，通过将其转换为拟阵中值问题[28]，给出了1个多项式时间内的(7.081+ϵ)-近似算法。针对优先级k-供应商问题，BAJPAI等[29]给出了1个多项式时间内的3-近似算法。LEE等[30]考虑了欧氏空间的优先级k-供应商问题，通过将其转换为最小边覆盖问题[31]，给出了多项式时间内近似比为的近似算法。

算法的时间复杂度与输入实例大小和参数相关，目前还没有解决该问题的固定参数可解时间内的近似算法。目前，大多数算法在解决优先级k-中心问题或相关问题时，都是基于贪心策略来选取中心点。受贪心策略的启发，本文提出了新的中心点选取方法，该方法通过选择一定规模的候选中心点集，并且保证该候选中心点集中存在非常接近最优解的可行解，从而将原先的近似比2改进为(1+ϵ)，其中ϵ是用于控制算法近似比的参数。相比于先前的算法，本文提出的算法近似比更小，求解的近似解与最优解之间的差距更小。当ϵ趋于0 时，该近似比将无限趋近于1，表明该算法给出的近似解无限接近问题实例最优解，在实际应用中具有更好的效果。优先级k-中心问题及相关问题的研究现状见表1。

表1 优先级k-中心问题及相关问题近似结果Table 1 Approximate results for priority k-center and related problems

3 优先级k-中心问题算法

给定优先级k-中心问题的1 个实例I=(X，d，k，r)，基于k-中心问题的贪心策略，提出新的中心点选取算法Priority-k-Center。下面证明本文提出的算法近似比为(1+ϵ)，时间复杂度为(kϵ-1)O(k)·nO(1)，其中，n=|X|。

给定优先级k-中心问题的实例I=(X，d，k，r)，算法Priority-k-Center 主要包含2 步：首先，通过调用算法Selection 得到大小为k·(4/ϵ)D的候选中心点集合T，其中D为集合X的加倍度量维度。然后，对集合T中每个大小为k的子集S，调用算法Assignment 将集合X中的点分配给子集S，最后输出代价最小的子集S。算法Priority-k-Center 的具体过程如图1所示。

图1 求解优先级k-中心问题算法Fig. 1 An algorithm for the priority k-center problem

下面给出本文的主要结果。

定理1：给定优先级k-中心问题的1个实例I=(X，d，k，r)和实数ϵ＞0，算法Priority-k-Center 给出了实例I的(1+ϵ)-近似解，其时间复杂度为(kϵ-1)O(k)·nO(1)，其中，n=|X|。

3.1 候选中心点集的选取

算法Selection 的主要思路是利用贪心策略选取更多的候选中心点，使得候选中心点中存在一些点接近最优中心点。算法Selection 首先调用k-中心问题的1 个贪心算法，记为k-Center，得到k个中心点。算法k-Center的具体过程如下：给定k-中心问题的1个实例(X，d，k)，k-Center首先在集合X中随机地选取1 个点作为初始中心点，然后，对于剩余的每个点，计算距最近现有中心的距离，选择与其最近中心的距离最大的点作为下一个中心，迭代上述过程至k个中心点被选择为止。

定理2[8]：给定k-中心问题的1个实例(X，d，k)，算法k-Center 是k-中心问题的1 个2-近似算法，其时间复杂度为O(|X|k)。

上述定理说明当选取的中心点数量为k时，能得到1个2-近似解。因此，若选取更多的中心点，则基于选取中心点得到的聚类代价与最优解代价的差值变小。基于上述分析，算法Selection 的具体过程如下：给定优先级k-中心问题的1 个实例I=(X，d，k，r)和实数ϵ＞0，算法Selection 首先调用k-Center(X，d，k)得到1 个大小为k的集合U；令T=U，选择距离集合T最远的数据点并加入集合T中，迭代上述过程至C(T) ＞(ϵ/2)·C(U)，其中，ϵ为近似比控制参数。算法Selection 的具体过程如图2所示。

图2 候选中心点集的选取算法Fig. 2 A selection algorithm for candidate centers

引理1：给定优先级k-中心问题的1个实例I=(X，d，k，r)和实数ϵ＞0，算法Selection返回1个大小为k·(4/ϵ)D的集合T，其中，D为集合X的加倍度量维度。算法Selection的时间复杂度为O(nk·(4/ϵ)D)，其中，n=|X|。

证明：令集合T为算法Selection返回的解。这里首先证明|T|=k·(4/ϵ)D，其中D为集合X的加倍度量维度。令集合U为算法Selection 第二步返回的结果。若集合X中的每个点被分配到集合U中最近的中心点，则集合X被划分为k个集合，其中每个集合的半径不超过C(U)。基于加倍度量空间的性质，对于其中任意的1 个集合，都可以最多被(4/ϵ)D个集合覆盖，其中，每个集合的半径不超过(ϵ/4)·C(U)，因此，共存在最多k·(4/ϵ)D个这样的集合可以覆盖集合X。当|T|=k·(4/ϵ)D时，算法Selection 停止执行，此时，C(T)≤(ϵ/2)·C(U)成立。假设当|T|=k·(4/ϵ)D时，C(T) ＞(ϵ/2)·C(U)，即存在一些点y∈X，使得d(y，T)＞(ϵ/2)·C(U)成立。由于贪心策略每次选取距离集合T最远的点作为中心点，因此，集合T中任意2 点之间的距离至少为d(y，T)，否则，点y将作为中心点被添加到集合T中。又因为d(y，T)＞(ϵ/2)·C(U)，所以，T∪{y}中任意2 点之间的距离大于(ϵ/2)·C(U)。由上述证明可知，共存在最多k·(4/ϵ)D个半径不超过(ϵ/4)·C(U)的集合覆盖集合X。因为|T∪{y}|=k·(4/ϵ)D+1，所以，在同一个集合中，T∪{y}中一定存在2 点（记为t1和t2），基于三角不等式，有

这与T∪{y}中任意2 点之间的距离大于(ϵ/2)·C(U)矛盾。因此，当算法Selection 停止执行时，|T|=k·(4/ϵ)D。

由定理2可知，算法Selection第二步时间复杂度为O(nk)。算法Selection 最多执行k·(4/ϵ)D次循环，其中，每次花费O(n)时间遍历集合X去选择距离集合T最远的点，因此，算法Selection的时间复杂度为O(nk·(4/ϵ)D)。

给定优先级k-中心问题的1 个实例I=(X，d，k，r) 和实数ϵ＞0，令集合T为调用算法Selection 返回的解。下面证明集合T中存在1 个大小为k的子集S，其中S产生的代价接近实例I最优解产生的代价。

引理2：令集合T为算法Selection 返回的解，则一定存在1 个大小为k的子集S⊆T，使得，其中，为实例I的最优解代价。

证明：令为优先级k-中心问题实例最优解，R*为k-中心问题实例最优解。因为优先级k-中心问题实例(X，d，k，r)的解也是k-中心问题实例(X，d，k)的解，所以，。令表示Ip的最优解，对任意i∈{1，2，…，k}，令表示集合T中距离点最近的点。对任意v∈X，不失一般性，假设点v属于点所在的最优簇。根据三角不等式，有

因此，一定存在1 个大小为k的子集，使得。

3.2 分配算法

给定优先级k-中心问题的1 个实例I=(X，d，k，r) 和实数ϵ＞0，令集合T为调用算法Selection 返回的解。对于集合T中任意1 个大小为k的子集，算法Assignment 将集合X中的点分配给该子集，并输出得到的聚类代价。实际上，算法Priority-k-Center 最后输出代价最小的子集S。算法Assignment 中的参数R*p是优先级k-中心问题实例的最优解。对于优先级k-中心问题的1 个实例I=(X，d，k，r)，I的最优解值是集合X中某2 点间的距离，所以，通过枚举集合X中2点间的所有距离可以得到实例I的最优解值。算法Assignment的具体过程如图3所示。

图3 分配算法Fig. 3 An assignment algorithm

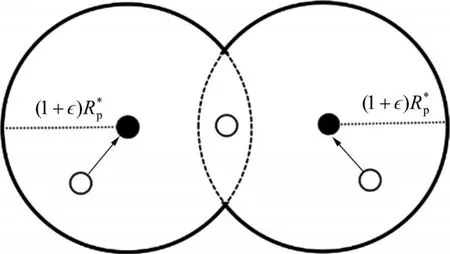
图4 2个数据点集合相交情况示例Fig. 4 An example for two intersecting doint sets

因为优先级k-中心问题是优化点到中心点距离与其优先级之间的比值，所以，对∀v∈H，无论将点v分配给si或者sj，都不会影响集合X中点到集合S的最大距离与其优先级的比值最小的目标。根据就近原则，若将集合X中点分配到集合S中距离其最近的中心点，则这种分配方式产生的代价最多为。

综上所述，若集合S⊆T是实例I的1个ϵ-近似解，则算法Assignment 按照最近分配原则产生的代价不超过。

因为将数据点分配给集合S花费的时间为O(nk)，所以，算法Assignment 的时间复杂度为O(nk)。

3.3 时间复杂度分析

由引理1可知，选取候选中心点集T的时间复杂度为O(nk·(4/ϵ)D)。考虑集合T中所有大小为k的子集，当加倍维度D为常数时，枚举的次数为|T|k=kk·(4/ϵ)kD=(kϵ-1)O(k)。

对于集合T中每个大小为k的子集S，由引理3可知，算法Assignment 的时间复杂度为O(nk)。因此，算法Priority-k-Center 总的时间复杂度为(kϵ-1)O(k)·nO(1)。

综上所述，定理1成立。

4 结论

1) 对优先级k-中心问题基于贪心策略，提出了新的中心点选取方法，利用加倍度量维度的性质去限制中心点集合的大小，并给出了相应证明，实现了1个FPT时间内的(1+ϵ)-近似算法，降低了目前求解该问题的近似比。

2) 带噪声的优先级k-中心问题仍然没有给出FPT时间内的近似算法，能否应用本文提出的算法解决该问题仍有待进一步研究。