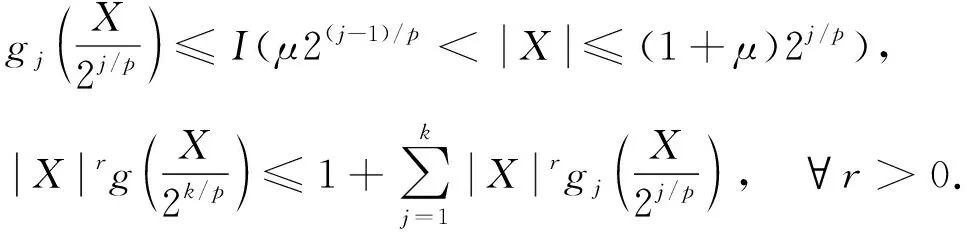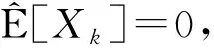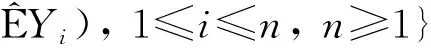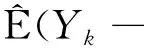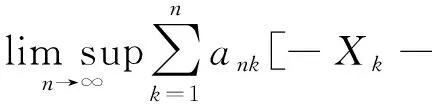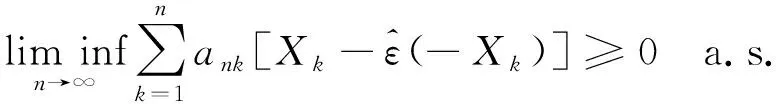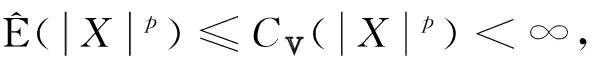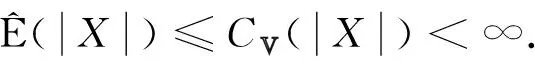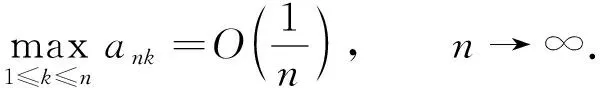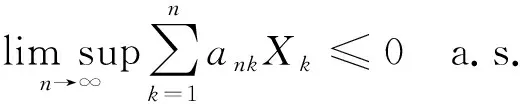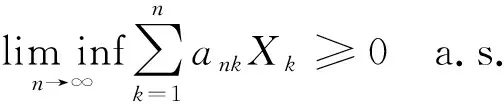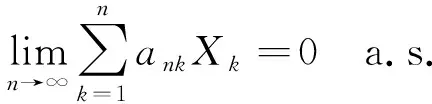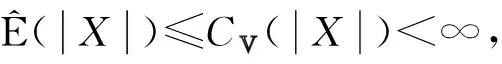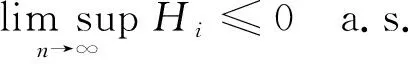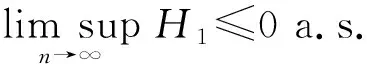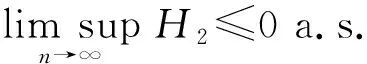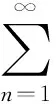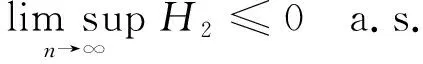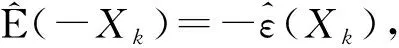次线性期望下m-END序列加权和的几乎处处收敛性

谭希丽, 董 贺, 孙佩宇, 张 勇

(1. 北华大学 数学与统计学院, 吉林 吉林 132013; 2. 吉林大学 数学研究所, 长春 130012)

1 引言与预备知识

随着信息技术的飞速发展, 需要处理的高维随机数据也逐渐增多, 因此在统计、 金融和风险度量等领域出现了不确定性的实际问题, 而经典概率理论在处理这类非线性问题时有很大的局限性. 为此, Peng[1-3]提出了次线性期望完整的理论体系, 该体系可以很好地解决实际问题中的非线性问题. 目前, 次线性期望空间下的理论已得到广泛关注, 例如: Zhang[4-6]得到了次线性期望下广义独立和END(extended negatively dependent)随机变量序列的强极限定理、 矩不等式和Rosenthal不等式; Guo等[7-8]得到了次线性期望下m相依随机变量序列的中偏差和生成线性过程的中心极限定理; Dong等[9]研究了次线性期望下m-END随机变量阵列加权和的完全收敛性.

强大数定律是衡量数据序列稳定性的重要指标. 在Peng[1-3]的理论基础上, 研究者们已把概率空间下的强大数定律推广到了次线性期望空间下, 例如: Zhang等[10]得到了次线性期望下的Marcinkiewicz强大数定律; Hu[11]证明了次线性期望下一般矩条件的强大数定律; Chen等[12]得到了次线性期望下ND(negatively dependent)随机变量序列的强大数定律; Wang等[13]得到了次线性期望下END序列的几乎处处收敛性; 谭希丽等[14]研究了次线性期望下WOD(widely orthant dependent)随机变量序列加权和的几乎处处收敛性; Zhan等[15]得到了次线性期望下END随机变量序列加权和的几乎处处收敛性; 文献[16-17]分别证明了次线性期望空间下END列加权和与END列Jamison型加权和的几乎处处收敛性. 本文讨论次线性期望下m-END随机变量序列的强大数定律, 并将经典概率空间中END序列的几乎处处收敛性推广到次线性期望下的m-END序列中.

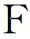
这里常数c>0,m∈依赖于φ.称为随机变量空间, 记为X∈.

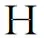
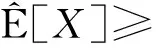
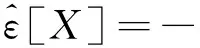
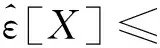
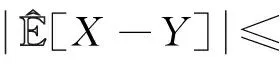
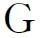
1)V(Φ)=0,V(Ω)=1;

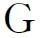
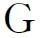
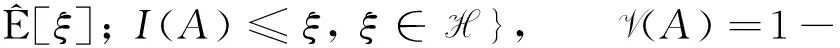
其中Ac为A的补集.

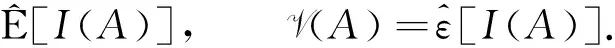
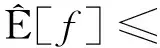
定义3[5]Choquet积分为

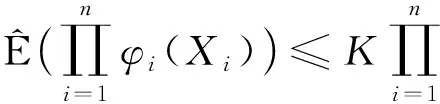
则随机变量序列{Xn,n≥1}称为上(下)END序列, 其中非负函数φi∈Cl,Lip()是非降(非增)的.如果该序列既是上END序列又是下END序列, 则称该序列是END序列.

受END定义的启发, Dong等[9]给出了次线性期望空间下m-END序列的定义.

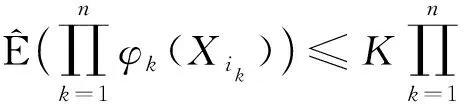
|ik-ij|≥m, 1≤k≠j≤n,

这里非负函数φi∈Cl,Lip()是非降(非增)的.如果该序列既是上m-END序列又是下m-END序列, 则称该序列是m-END序列.

显然, 如果{Xn,n≥1}是m-END随机变量序列,f1(x),f2(x),…∈Cl,Lip()都是非降(或非增)函数, 则{fn(Xn),n≥1}也是m-END随机变量序列.

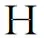
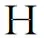
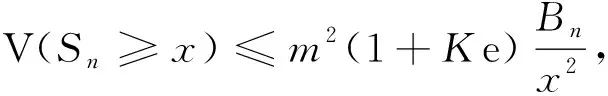
(1)

则存在一个正常数Cp≥1, 使得对∀x>0, 0<δ≤1,n≥m, 有

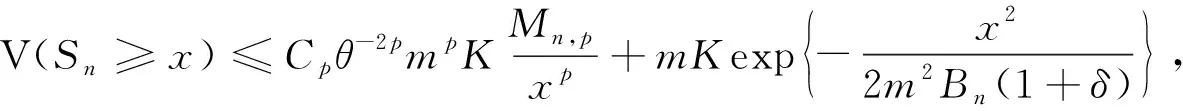
(2)

其中K是m-END随机变量序列定义的控制常数.

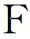
2 主要结果

定理1设{Xn,n≥1}是次线性期望下的上m-END随机变量序列, 容度V具有可数次可加性.存在一个随机变量X, 使得对00), 满足

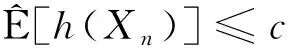
(3)

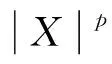
(4)

当p≥1时, 假设

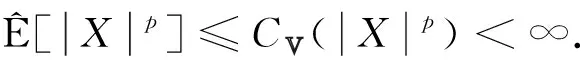
(5)

令{ank,n≥1, 1≤k≤n}是正实数列, 使得

(6)

则

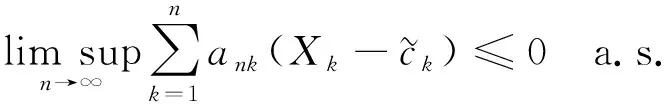
(7)

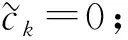
此外, 如果{Xn,n≥1}是下m-END随机变量序列, 则

(8)

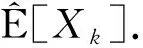
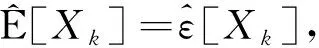
(9)

则对于1≤p≤2, 有

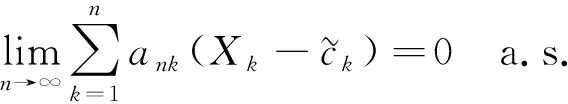
(10)

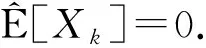
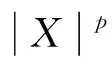
注意到

因此对∀c>0, 有

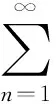
(11)

再注意到

因此由式(11)可得

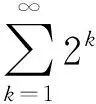
(12)

对于上m-END随机变量序列{Xn,n≥1}, 为确保截断后的随机变量也是上m-END随机变量序列, 需要截断函数属于Cl,Lip且是非降的, 对任意的1≤k≤n,n≥1, 有fc(x)=-cI(x<-c)+xI(|x|≤c)+cI(x>c), 记

Y=f(ε/32)n1/p(X),Z=X-Y.

由于fc(x)∈Cl,Lip且是非降的, 因此{Yk, 1≤k≤n,n≥1}也是上m-END随机变量序列.注意到

因此要证明式(7), 只需证

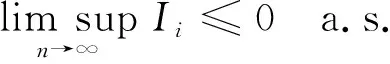
对于0<μ<1, 假设函数g(x)∈Cl,Lip(), 且g(x)在x≥0上单调下降, 使得∀x∈, 有0≤g(x)≤1; 当|x|≤μ时,g(x)=1; 当|x|>1时,g(x)=0.则有

I(|x|≤μ)≤g(|x|)≤I(|x|≤1),I(|x|>1)≤1-g(|x|)≤I(|x|>μ).

(13)

因此V(Zk≠0, i.o.)=0.由引理2、 V具有可数次可加性和式(6)可得

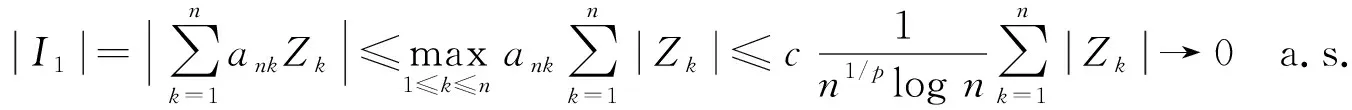
(14)

其次, 证明|I3|→0, a.s.n→∞.对任意的r>0, 结合Cr不等式和式(13), 可得

因此

(i) 0

由式(11)和V(|X|>μn1/p)(n≥1)是递减的, 可得

因此

I″→0,n→∞.

(16)

对于0<μ<1, 令gj(x)∈Cl,Lip()(j≥1), 使得∀x∈, 有0≤gj(x)≤1; 当2(j-1)/p<|X|≤2j/p时,当|x|≤μ2(j-1)/p或|x|>(1+μ)2j/p时,则有

(17)

对每个n, 均存在一个常数k, 使得2k-1≤n<2k, 结合式(17)及g(x)在x≥0上单调下降, 可得

由式(12)可得

I′→0,n→∞.

(18)

再结合式(16)和式(18)可得

I3→0,n→∞.

(19)

再结合式(5)和式(6), 可得

综合(i)和(ii), 并结合式(19)和式(20), 可得

I3→0,n→∞.

(21)

下面证明I21<∞和I22<∞.先证I21<∞, 由式(6)和式(15), 可得

由式(12)得

只需证I212<∞.由式(12)和q≥2, 可得

即I21<∞.

下面证明I22<∞.因为

所以

对∀ε>0, 根据引理2和式(22), 可得

(23)

再结合式(14)、 式(19)和式(23), 可得式(7)成立.

如果{Xn,n≥1}是下m-END随机变量序列, 则{-Xn,n≥1}是上m-END随机变量序列, 且{-Xn,n≥1}也满足定理的条件, 所以可用{-Xn,n≥1}代替{Xn,n≥1}, 并代入式(7)得

从而有

即式(8)成立.证毕.

即推论1的条件满足定理1的条件, 因此直接可得结论.

定理2设{X,Xn,n≥1}是次线性期望下同分布的上m-END随机变量序列, 容度V具有可数次可加性, 满足

(24)

令{ank,n≥1, 1≤k≤n}是正实数列, 使得

(25)

则

(26)

此外, 如果{Xn,n≥1}是同分布的下m-END随机变量序列, 则

(27)

特别地, 如果{Xn,n≥1}是同分布的m-END随机变量序列, 则

(28)

(29)

对于上m-END随机变量序列{Xn,n≥1}, 为确保截断后的随机变量也是上m-END随机变量序列, 需要截断函数属于Cl,Lip且是非降的, 对任意的1≤k≤n,n≥1, 设fc(x)=-cI(x<-c)+xI(|x|≤c)+cI(x>c), 记

Yk=-nI(Xk<-n)+XkI(|Xk|≤n)+nI(Xk>n),

Zk=Xk-Yk=(Xk+n)I(Xk<-n)+(Xk-n)I(Xk>n),

由定义6可知, {Yk, 1≤k≤n,n≥1}和{Zk, 1≤k≤n,n≥1}也是上m-END随机变量序列.

注意到

因此为证式(26), 只需证

(30)

因此V(Zk≠0, i.o.)=0, 由引理2和V具有可数次可加性, 并结合式(25)可得

因此

对∀ε>0, 根据引理2可得

(32)

再结合式(31)和式(32), 可得式(26)成立.

从而有

即式(27)成立.

特别地, 如果{Xn,n≥1}是m-END随机变量序列, 则式(28)可直接由式(26)和式(27)得到.证毕.

注1在经典概率空间下, 定理1将文献[16]中的定理1推广到了次线性期望空间, 得到了更一般的结果.在次线性期望空间下, 定理1和推论1分别将文献[13]中的定理1和文献[15]中的推论3.1从END随机变量序列推广到了m-END随机变量序列.

注2定理2将文献[18]中的定理2从经典概率空间推广到了次线性期望空间. 在次线性期望空间下, 定理2将文献[15]中的END随机变量序列的相关结果推广到了m-END随机变量序列, 得到了更具一般性的结果.且当0≤p≤1时, 定理1的条件强于定理2.

注3当m=1时,m-END随机变量序列即为END随机变量序列. 由于END随机变量序列包括ND等随机变量序列, 因此定理1、 推论1和定理2对END和ND等一类随机变量序列仍有效. 本文结果可应用于股票期权定价等金融、 保险的不确定性问题中.