基于非结构化网格的大规模磁测数据正则化反演研究

刘阳，张志勇

（东华理工大学 地球物理与测控技术学院，江西 南昌 330013）

磁法勘探已广泛应用于铀矿勘探、深部地质构造圈定、地热调查等领域［1-4］，大规模铀矿地质勘探亟需准确、高效的磁法解译。位场正演是磁法勘探解释任务的基础，其计算成本依旧是阻碍三维反演发展的一个严重问题［5］。位场正演模拟主要有空间域和频率域两类方法，其中空间域方法在处理起伏地表与非规则离散模型等方面具有较大优势。空间域方法又可分为解析法和数值法。通过闭合积分公式建模的空间域方法已有众多研究成果［6-7］，简单矩形棱柱积分公式难以拟合复杂地质体，均匀多面体剖分算法逐渐成为位场正演建模的主流［8］。然而，三维复杂地质模型计算公式复杂，适应性较差、计算量较大［9］，以解析法正演开展大规模离散反演时需要大量积分运算和内存消耗，计算成本巨大，因此，位场解析法建模的应用受到了限制。

位场数值法建模主要有有限差分法［10］、有限体积法［11-12］、积分方程法［13］、有限单元法等［14］，与解析法相比，数值法计算精度略低，但计算时间和内存消耗方面具有一定优势。其中有限差分法通常采用结构化网格，但在物性参数复杂分布或场域分布几何特征不规则时适应性差，存在一定局限性。有限单元法既可采用结构化网格，也可采用非结构化网格。与结构化网格相比，非结构化网格在要求较高精度或可接受较低精度的区域，网格的局部细化或粗化可以在不影响这些区域以外的网格的情况下执行［12］。因此，使用非结构化网格的数值格式会有更高的精度、更低的计算时间和内存占用。有限单元法以其适用性强、可以模拟任意复杂地形及地质体而受到广泛运用［15-17］，如地震［18］、直流电阻率［15］、自然电位［19］、大地电磁［20］正反演中均得到应用。前人基于有限单元法开展了大量位场正反演的研究，Zhang等［21］将遗传算法与有限单元法相结合实现了一种替代方法反演重力异常数据，重建地下三维密度结构；Cai 等［14］通过一种快速的有限单元法来解决复杂地质条件下引力位的边值问题；Maag 等［22］由重力位的偏微分方程出发推导出基于有限单元法的正演和反演问题；Jahandari 和Farquharson［12］采用有限单元法和有限体积法与解析法对比实现了重力位正反演；但当前文献少有以非结构化有限单元法开展磁场正反演的研究。

大规模磁测数据反演中，灵敏度矩阵的储存与计算一定程度上制约着计算规模的大小。通过将灵敏度矩阵及其转置与向量乘积转换为正演过程，进行有限内存最优化求解的反演策略已应用到地球物理反演问题中，其中算法包括共轭梯度法［23］、有限内存拟牛顿法［24-25］、高斯-牛顿法［26］等，与其他最优化算法相比，高斯-牛顿法在保证快速收敛的同时，有效减少了计算量，因此，高斯-牛顿法适用于大规模磁测数据反演。

针对以解析法正演为依托的磁异常反演及规则网格数值解对复杂地质体拟合程度不足、计算成本大等缺点，本文采用非结构化网格有限单元法进行磁异常正演，通过灵敏度矩阵隐式存储的高斯-牛顿方法求解反演目标函数实现磁测数据正则化反演。研究工作首先采用局部网格加密技术和最小二乘空间梯度计算方法提高有限单元正演计算精度，通过与解析法对比，对非结构化网格有限单元法正演精度的影响因素进行了试算讨论；在此基础之上，开展了理论模型与铀矿区域实测数据的反演，验证了本文提出的三维磁测数据反演算法的可行性。

1 三维有限单元正演

1.1 正演理论

在假设无传导电流的空间域，磁位基本方程可表示为：

式中：μ0为真空磁导，H/m；U为磁位；κ为磁化率；∇为哈密尔顿算子；Mr为剩余磁化强度矢量，A/m。当在两种介质存在的空间域中，采用有限单元法求解方程式（1），考虑到两种介质分界面磁位连续且无散场的特点，得到公式：

式中：n为分界面上的单位正法线方向；μ1和μ2为边界两种介质中的磁导率；U1和U2为边界两种介质中磁位；Mr1和Mr2为边界两侧介质中剩余磁化强度矢量，Mr1，n和Mr2，n是Mr1和Mr2在 外法向的投影，则有第一类边界条件：

式中：T为总磁场强度矢量，T；r为坐标原点到无穷远边界距离矢量。第二类边界条件可表示为：

磁场边值问题与求解下式变分问题等价：

式中：Tn是磁场T在边界外法线方向上的投影，Ω 为研究区域。对计算区域进行非结构化四面体离散，在每个剖分单元采用线性函数插值，对各单元泛函求和，得到下列线性系统：

式中：K为刚度矩阵（对称稀疏矩阵）；U为节点磁位；P为边界条件形成源项。求解联立方程组可得到各节点磁位U，通过数值微商可得到各磁场分量，但由于非结构化网格中网格大小不一致，基于线性插值计算磁位，对磁位进行求导磁场为常数，使得在计算磁场时的精度和稳定性存在问题。本文拟采用与观测点共点的所有四面体进行空间梯度的最小二乘计算。假设定义观测点坐标为(x0，y0，z0)，相应磁位为U，与观测点共点的所有四面体n 个顶点坐标定义为(xi，yi，zi)，相应磁位为Ui，其中i=1，2…n，则有：

节点组成方程组为：

可将式（9）表示为：

令E=(U-AL)T(U-AL)，对L 进行求导可得：

令上式为0，得L=(AT A)-1ATU，求解方程可得到坐标点处梯度为：

进而可得到观测点处磁场强度。

1.2 正演精度影响因素分析

正演精度直接影响反演的可靠性，对于非结构化有限单元正演，其精度受多种因素影响。本文从观测网格密度、边界节点数两方面进行讨论，并与均匀多面体的闭合积分公式［27］计算出的总磁异常进行精度对比。设计模型如图1所示，假设在地下空间磁化率为0.006 SI 的背景中，设置一个磁化率为0.1 SI 的异常体，异常体顶板埋深为500 m，结构为1 000 m×1 000 m×1 000 m，地磁场强度在X、Y、Z 三个方向的分量分别为（30 000 nT，0 nT，40 000 nT）。选取观测区任意部分区域测点验证有限单元法的计算精度，计算区域大小为250 m×250 m。

图1 磁化率模型Fig.1 Magnetic susceptibility model

1.2.1 观测网格影响

在有限单元计算中，以观测点作为剖分网格中心点进行剖分，因此，有限单元计算精度依赖于剖分网格到中心点的距离。对不同观测网格产生总磁异常进行计算，边界节点数为38，计算结果如图2 所示。不同观测网格的剖分网格属性及各类误差信息如表1 所示。随着观测网格变密，平均绝对误差从3.67 nT降至1.60 nT，最大绝对误差从14.08 nT 下降至5.56 nT，平均相对误差从0.047 下降至0.018，计算总磁异常精度明显提高。

表1 地表不同观测密度所产生的网格参数及各类误差信息表Table 1 Grid parameters and error information of different observing density

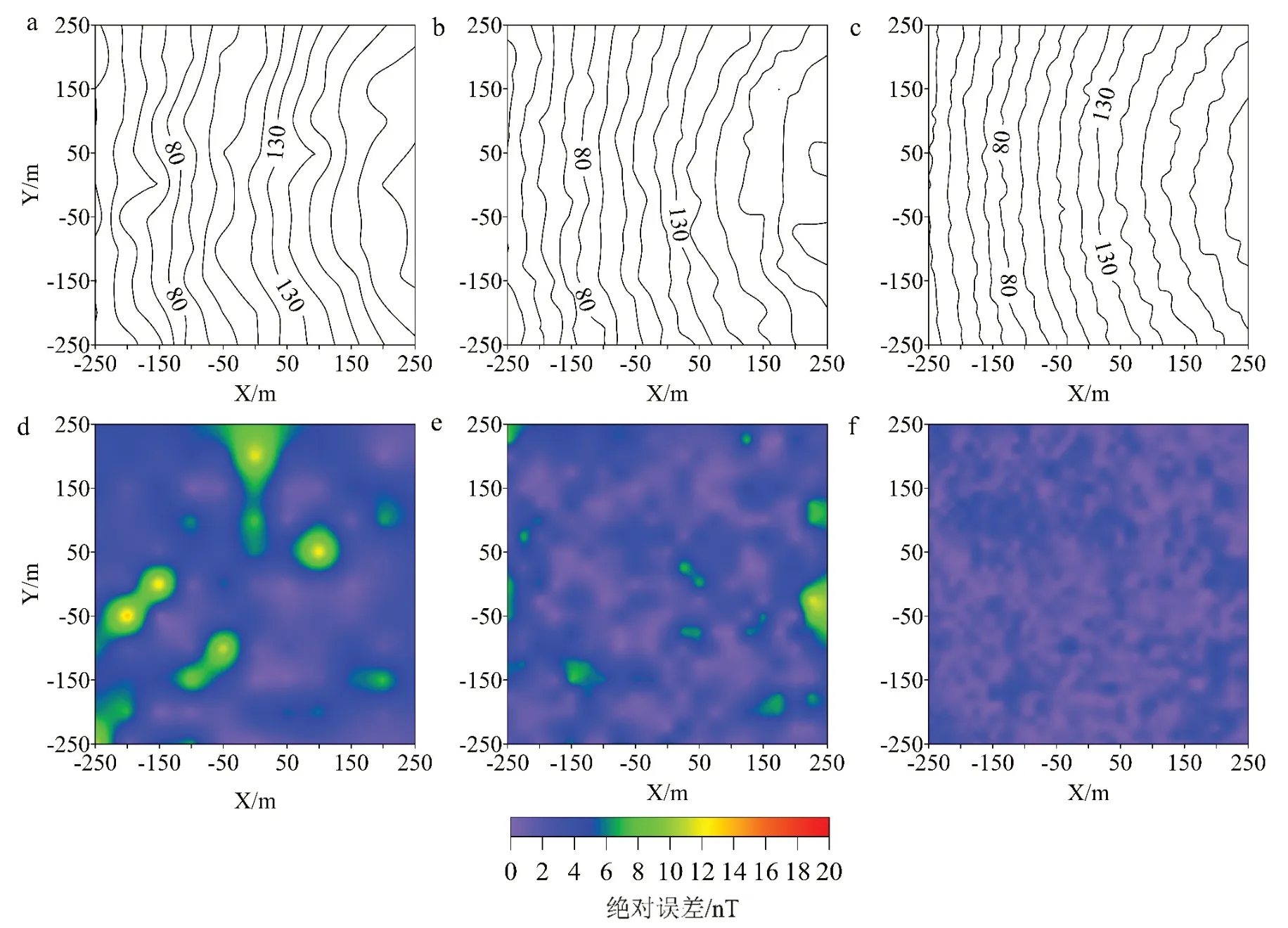
图2 不同观测网格下的总磁异常等值线及绝对误差图Fig.2 Contour of total magnetic anomaly and absolute error under different observation grids

1.2.2 边界节点数影响

为分析边界节点数对有限单元正演模拟计算的影响，选取边界节点［15，25，35，45］进行试算，观测网格为50 m×50 m，以1.2 倍指数扩边得到图3 和表2。计算结果显示，随着边界节点数的增加，平均绝对误差从80.15 nT 下降至3.77 nT，最大绝对误差从95.33 nT 下降至12.31 nT，平均相对误差从0.460 下降至0.046，最大相对误差减小，计算精度明显提高，而过少边界节点计算总磁异常存在较大的误差。

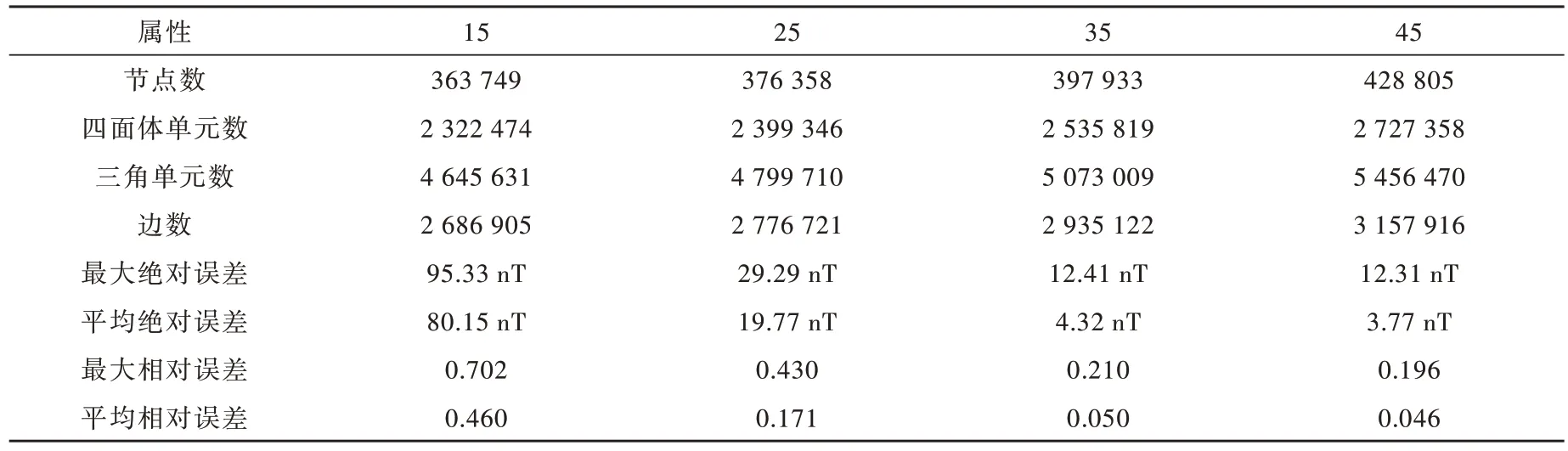
表2 不同边界节点数计算产生网格参数及各类误差信息表Table 2 Grid parameters and error information calculated with different boundary nodes

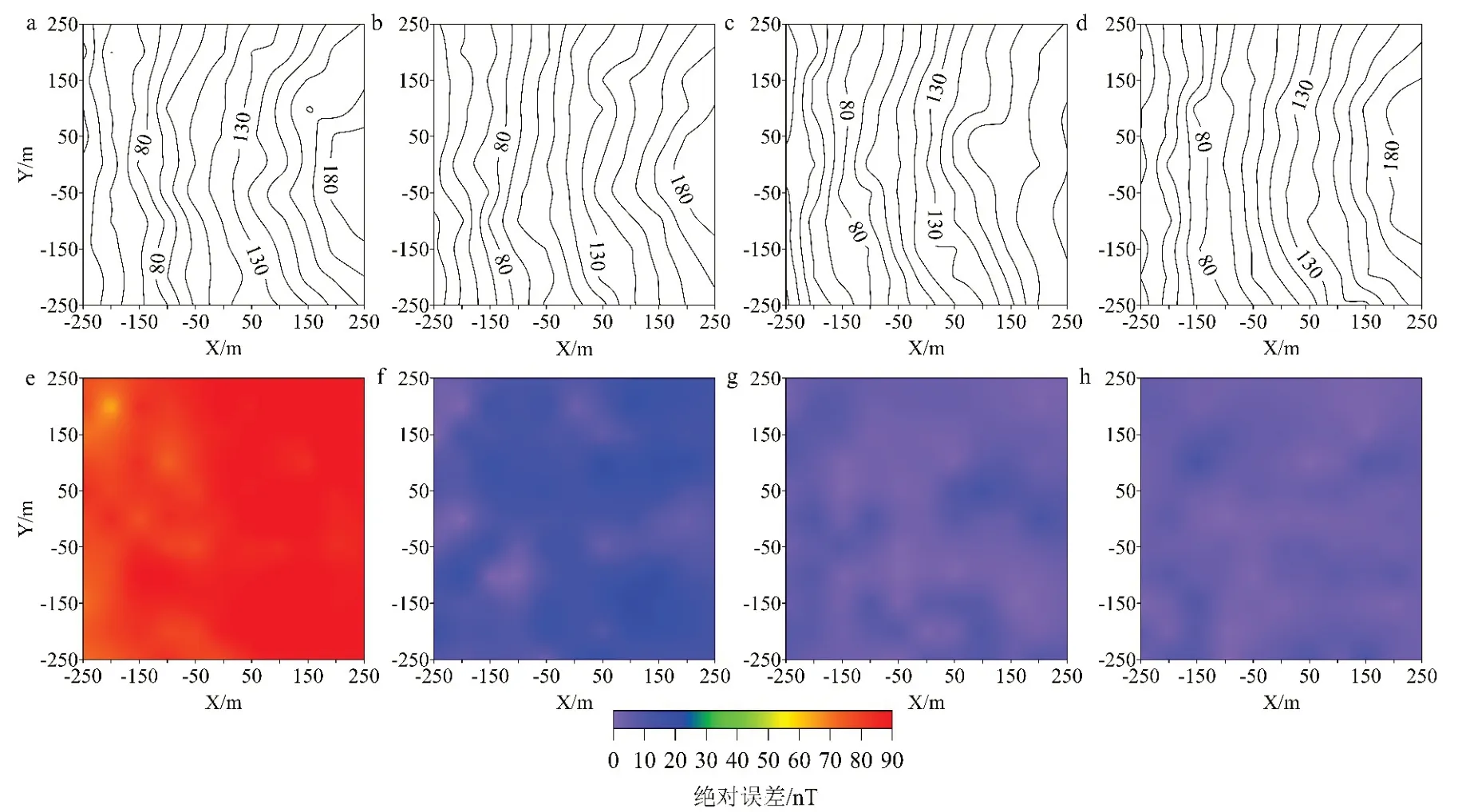
图3 不同边界节点数计算总磁异常等值线及绝对误差图Fig.3 Contour of total magnetic anomaly and absolute error calculated with different boundary nodes

1.2.3 局部网格密度影响

观测网格密度和边界节点数对于有限单元计算精度均有影响，而观测网格变密导致计算效率的下降，此外，观测网格密度达到一定程度，继续加密对于计算精度有较小的影响［15］。因此，本文采用网格加密的方式提高磁异常计算精度，网格加密的方法主要有局部体积加密方法（Local Volume-Refinement，简称LVR）、全局体积加密方法（Global Volume-Refinement，简称GVR）和局部测点加密方法（Local Node-Refinement，简称LNR）。其中GVR 法加密基于结构化网格会导致过多的冗余加密节点，精度提高不明显；LVR 法是在加密需求区域无应有的加密，反而在其他区域加入过多节点，导致计算量增大；LNR法相对于LVR 和GVR 法可以减少内存消耗和计算时间，因此，本文采用LNR 网格加密方式。

局部测点网格细化策略是基于观测点位置下方插入节点，观测网格为50 m×50 m，扩边节点数为45，得到计算结果如图4 和表3 所示。局部网格细化可提高正演计算精度，插入节点深度较浅时能获得更高精度的异常分辨率，当插入节点后剖分网格数量增加明显，而插入节点接近观测点时剖分网格数量明显多于插入节点较深的情况，当在观测点下60 m、20 m、1 m 插入节点时平均绝对误差从2.47 nT减小至1.11 nT，平均相对误差从0.028 下降至0.011，相比同一观测密度计算，局部网格加密后磁异常精度和稳定性明显提高。

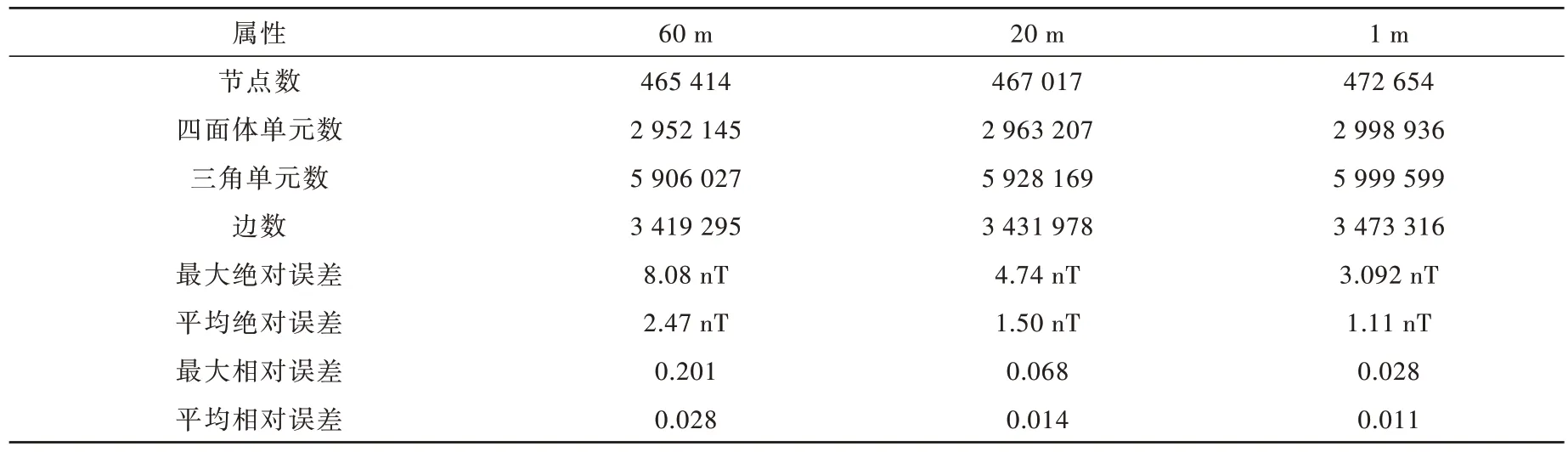
表3 不同深度插入节点产生网格参数及各类误差信息表Table 3 Mesh parameters and various error information calculated by inserting nodes at different depths

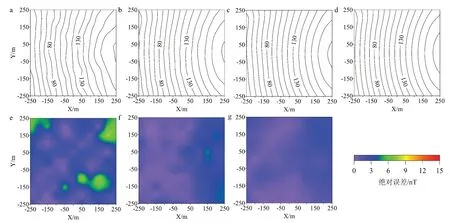
图4 不同深度插入节点计算磁异常等值线及绝对误差图Fig.4 Contour of magnetic anomaly and absolute error calculated by inserting nodes at different depths

以上试算结果表明，通过提高观测网格密度、增多边界节点数及采用局部网格细化技术等可实现非结构化网格有限单元法计算磁异常精确解。

1.3 有限单元计算效率分析

为说明非结构化网格有限单元法计算的低耗存和高效率的特点，本文测试平台为Intel（R）Core（TM）i7-9700F CPU@3.00 GHz，RAM 32.0 GB。在同样的观测网格及相同剖分网格参数下，进行有限单元法与解析法计算内存和时长的统计（表4 和图5）。如表4 和图5 所示，与解析算法相比，同样的计算条件和剖分网格参数下，有限单元法计算时长与内存需求明显优于解析算法。

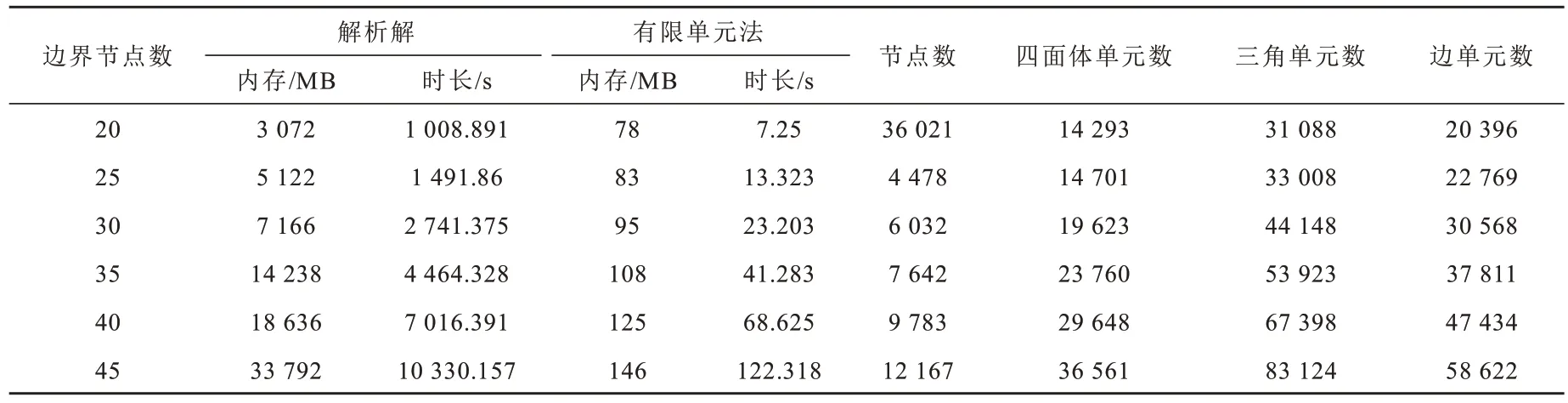
表4 有限单元法与解析法计算效率对比Table 4 Comparison of computational efficiency between finite element method and analytical method

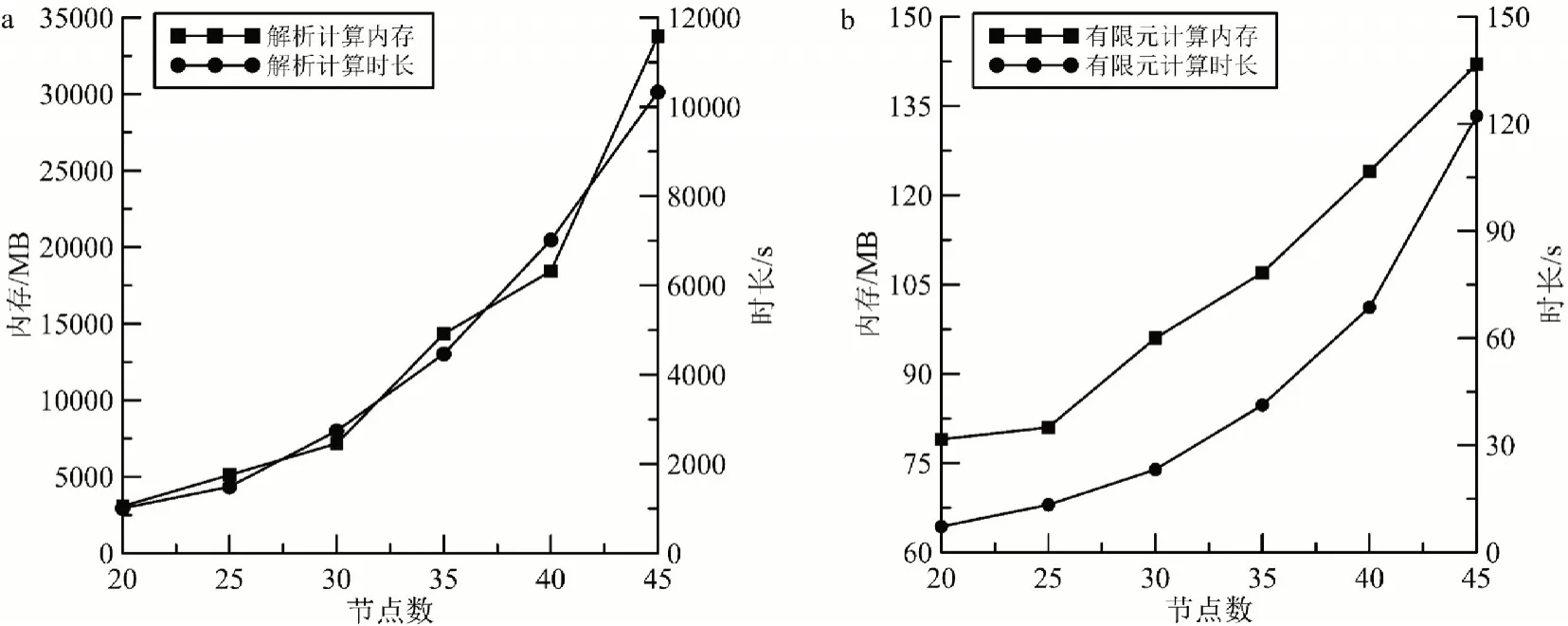
图5 计算内存与时长曲线对比图Fig.5 Contrast of calculation memory versus duration curve between the method of finite element and analysis

2 大规模磁测数据反演算法

2.1 正则化目标函数

正则化反演目标函数一般形式可表示为［28］：

式中：ϕd(m)为数据误差函数；ϕm(m)为模型稳定函数，本次研究工作采用最小结构稳定函数［29］；α为正则化因子，是平衡数据误差函数和模型稳定函数之间的权重系数，采用L-Curve 方法选取［30］；dobs为观测数据向量；m为离散模型向量；mapr为先验模型参数向量；A为正演算子；Wd为数据协方差矩阵；Wm为模型权重矩阵。

2.2 目标函数优化

本次研究工作采用高斯-牛顿方法求解目标函数：

式（13）数据误差项和模型稳定项展开可得：

将上述方程对Δm(n)求导，可得高斯-牛顿方程：

采用J表示灵敏度矩阵，J中任意元素表示为：

式中：Hi表示第i 个观测数据；m表示反演模型参数；mj为第j 个反演模型参数。将其与有限单元线性方程式（7）结合，则：

将上式代入式（19），可得：

将灵敏度矩阵及其转置与任意矩阵的乘积转换成线性方程的求解，并且该方程与有限单元具有相同的矩阵：

由式（25）和（26）所示，求取灵敏度矩阵（或转置）和任意矩阵的乘积可包含在灵敏度求解过程中，因此，实现了灵敏度矩阵的隐式储存，减少了内存消耗，提高了计算效率。

3 模型试算分析

3.1 单一模型

首先采用单一模型验证本文提出算法的可行性，单一模型和复杂模型正演数据中均加入5%随机噪声。模型设置如图1，采用总磁异常数据进行反演，观测网格为50 m×50 m，测点数为4 900 个，初始正则化因子为1.0×10-5，迭代75 次。如图6 所示，采用本文算法对单一模型反演取得了良好的效果，其中白色矩形框为模型位置，反演结果磁化率分布与真实模型位置有较好对应。从RMS 误差曲线可知（图7），随着迭代的进行，RMS 总体趋势稳定下降趋近于1.0，说明反演稳定收敛；反演中通过将灵敏度矩阵及其转置与任意向量的乘积转换成正演计算，内存需求减少，计算效率明显提高。

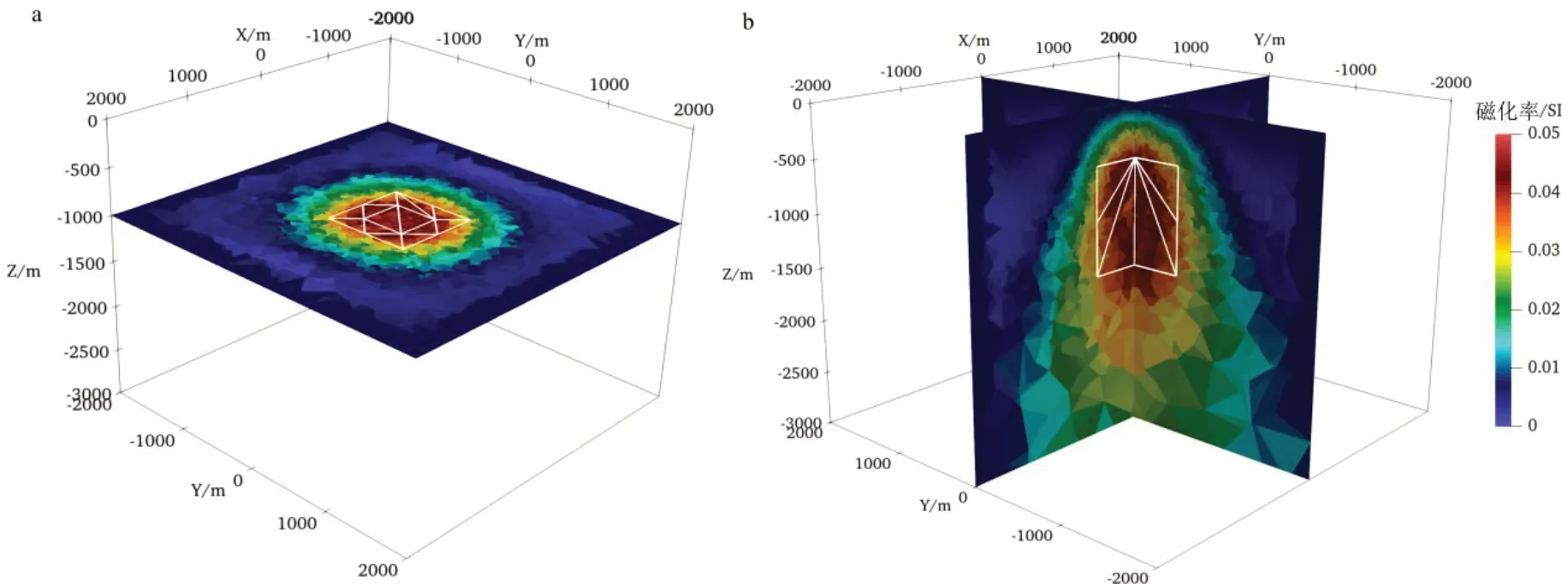
图6 单一模型反演结果Fig.6 Inversion results of single model

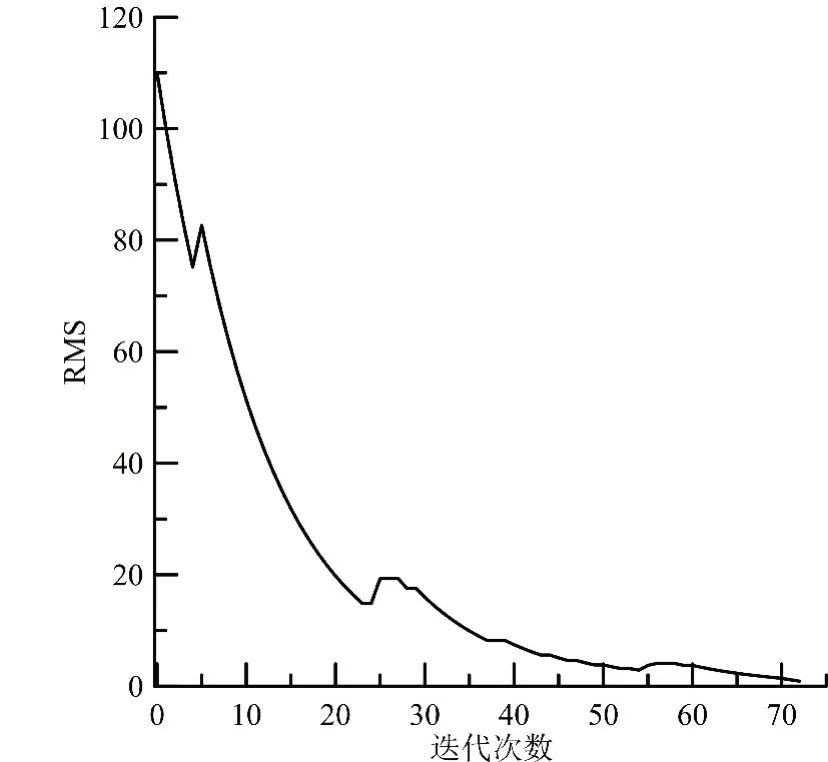
图7 单一模型反演RMS 误差曲线Fig.7 RMS error curve of inversion result by single model

3.2 复杂模型

为进一步测试本文提出的反演方法对复杂模型的反演效果，设置复杂磁化率模型如图8 所示。假设在地下空间磁化率为0.006 SI 的背景中，设置4 个磁化率均为0.1 SI 的矩形异常体，异常体结构及属性见表5，观测网格为50 m×50 m，测点数共计4 900 个，地磁场强度与单一模型等同。对于复杂模型进行磁化率反演取得同样效果（图9），反演磁化率分布位置与设定的4 个异常体模型位置均有对应，且反演磁化率横向分辨率有较好体现（图9a）。从复杂模型反演RMS 误差曲线可以发现（图10），RMS 随迭代次数逐渐下降并最终趋近于1.0，说明反演稳定收敛；相比解析法，以有限单元法开展复杂模型离散反演计算效率明显提高，试算结果表明，本文提出反演算法对于复杂模型同样具有可行性。

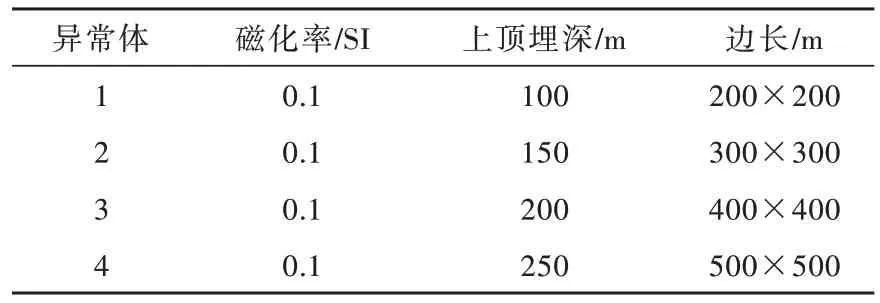
表5 异常体属性Table 5 Attributes of anomaly body

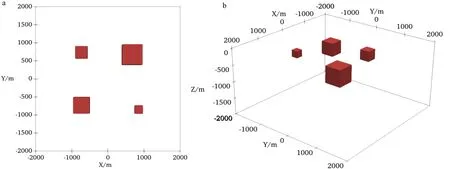
图8 设置磁化率模型Fig.8 Setting of the magnetic susceptibility model

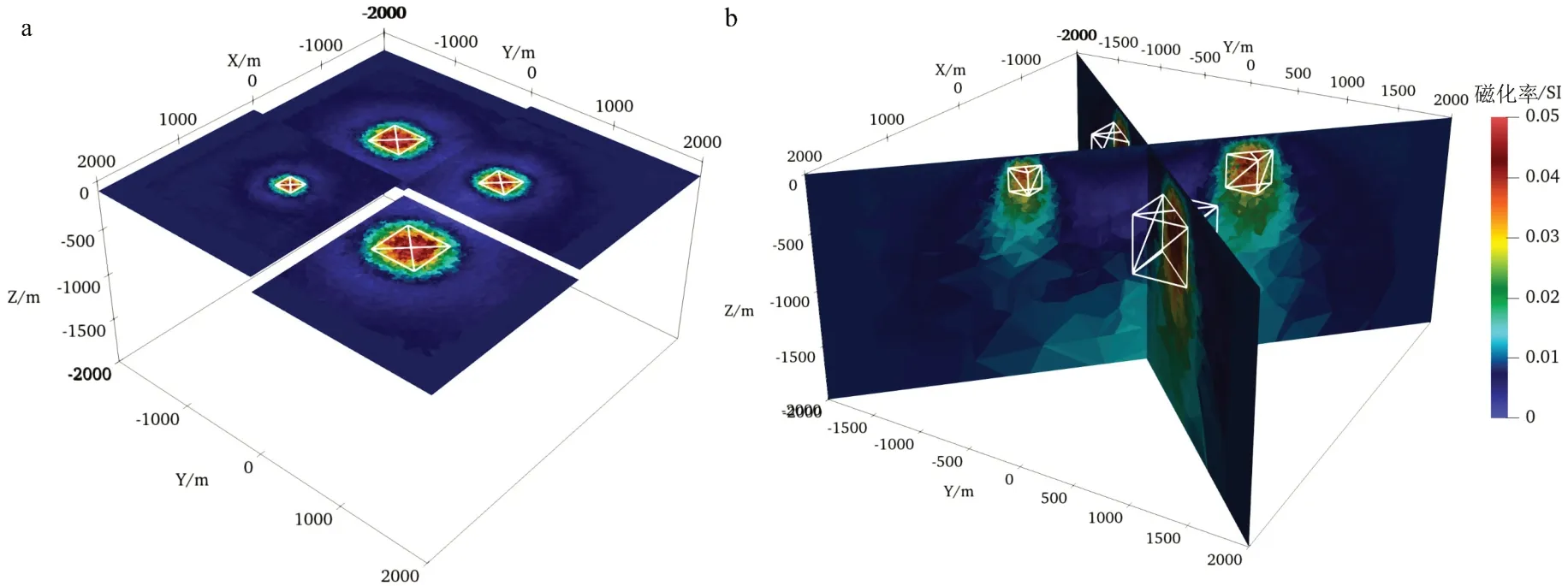
图9 复杂模型反演结果Fig.9 Inversion results of complex model

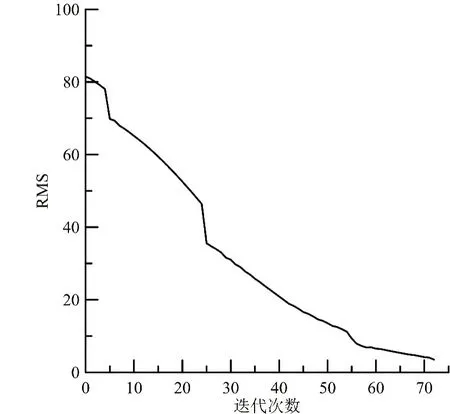
图10 复杂模型反演RMS 误差曲线Fig.10 RMS error curve of inversion result by complex model

3.3 实测数据反演

磁法在铀矿地质勘查中应用广泛，为验证本文提出算法处理铀矿区域采集实际数据的有效性，选取某铀矿研究区带地形磁测数据进行反演。研究区岩性以花岗岩为主，勘探目标为辉绿岩，观测网格为25 m×25 m，测点数共计3 025 个，研究区反演最高处为15 m，磁场强度为当地地磁场，磁异常为辉绿岩引起。初始正则化因子为1.0×10-8，共计迭代28 次。图11 a 为实测数据反演网格结果，反演节点数为62 841 个，四面体单元数为390 828 个，三角单元数为783 079 个，边数为455 091 个；图11b为反演结果横切图，切片深度分别为［10 m，-40 m，-70 m，-110 m］。

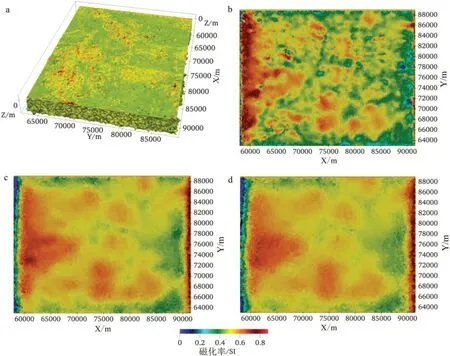
图11 实测数据反演结果Fig.11 Inversion results of measured data

如图11 所示，应用本文提出算法对实测数据进行处理得到较好的磁化率分布特征，模型边界分辨率高，异常特征明显，基于非结构网格其适用性强，具有模拟复杂结构的能力，对实测数据地形有较好的拟合。从实测数据反演RMS 误差曲线可以看出（图12），随着迭代次数RMS 整体呈下降趋势，说明实测数据反演同样稳定收敛。基于以上试算说明应用本文提出算法进行大规模带地形磁测数据反演具有有效性，为大区域铀矿地质勘查提供一定技术支持。

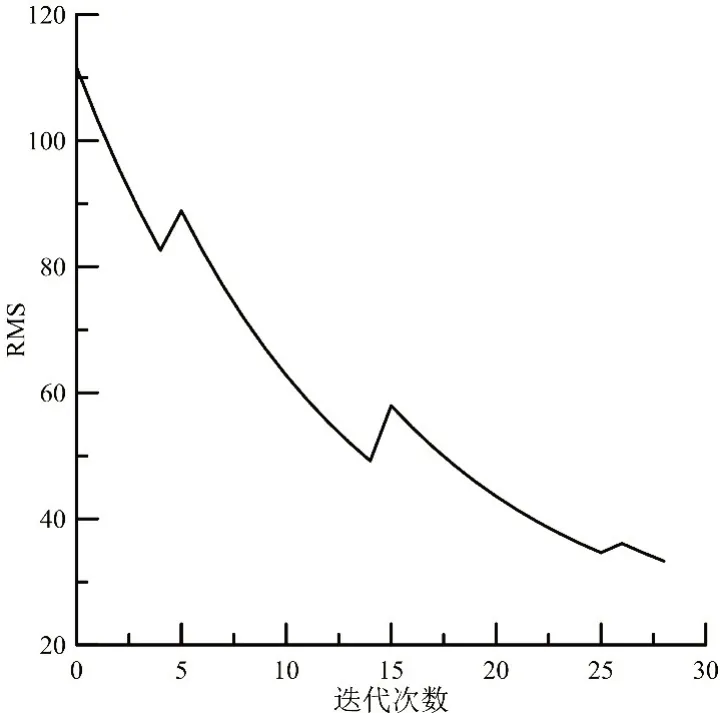
图12 实测数据反演RMS 误差曲线Fig.12 RMS error curve of inversion result from measured data

4 结论

本文开展了基于非结构化网格的大规模磁测数据三维正反演研究，分析了观测网格密度、边界节点数及局部网格细化等因素对正演精度的影响，探讨了利用灵敏度矩阵隐式存储的方法实现大规模磁测数据反演的算法，得到以下结论：

1）磁异常的非结构化网格的有限单元正演在内存消耗和计算效率两方面均优于解析算法。

2）非结构化网格有限单元正演的网格离散参数对计算精度有直接影响。提高观测网格密度、增多边界节点数并采用局部网格细化技术，可提高磁测数据正演的精度和稳定性。

3）非结构网格有限单元正演与灵敏度矩阵隐式存储的高斯-牛顿法反演相结合，有效减小了反演的内存消耗，降低了计算成本，适用于大规模三维磁测数据反演。