全局3-彩虹控制数与3-彩虹控制数之差为2和3的树的刻画

郝 国 亮, 曾 淑 婷, 庄 蔚, 谢 智 红

(1.东华理工大学 理学院,江西 南昌 330013;2.菏泽学院 数学与统计学院,山东 菏泽 274015;3.厦门理工学院 数学与统计学院,福建 厦门 361024;4.菏泽学院 商学院,山东 菏泽 274015 )

0 引 言

图的控制理论是图论中一个重要的研究领域,基于不同的研究背景,图的经典控制数衍生出了许多不同类型的控制参数[1-3],其中图的彩虹控制数的概念最早出现于2008年[4].随后,研究者们陆续给出了彩虹控制数的许多研究成果[5-8].Alqesmah等[9]和Amjadi等[10]分别引入了彩虹控制数的一个衍生变量,即图的全局彩虹控制数.Amjadi等[10]刻画了全局2-彩虹控制数与2-彩虹控制数之差为1和2的树.受此结果的启发,本文主要刻画全局3-彩虹控制数与3-彩虹控制数之差为2和3的所有树.

1 基本概念

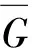
称无圈的连通图为树.在树中,度为1的顶点称为叶子点,只与1个叶子点相邻的顶点称为弱支撑点,至少与2个叶子点相邻的顶点称为强支撑点,弱支撑点和强支撑点统称为支撑点.双星图Sp,q是指恰好有2个支撑点的树且它们分别与p和q个叶子点相邻.称n≥3阶完全二部图K1,n-1为星形图,且称度为n-1的顶点为其中心.病态蜘蛛树是指对星形图K1,n-1(n≥3)至多剖分n-2条边所得到的图,称星形图的中心为病态蜘蛛树的头,称与头距离为1和2的叶子点分别为病态脚和健康脚.用Π表示有2个健康脚且至少有3个病态脚的病态蜘蛛树构成的集合.

2 主要结论

为得到本文的主要结果,首先给出下列引理.

引理1设u是树T中至少与3个叶子点相邻的强支撑点,则一定存在一个γr3(T)-函数f使得f(u)={1,2,3}且对任意与u相邻的叶子点x,f(x)=∅.

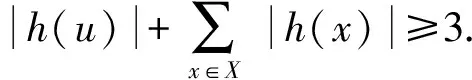
γr3(T)≤ω(f)=

ω(h)+3-3=

ω(h)=

γr3(T)

因此ω(f)=γr3(T).意味着f也是一个γr3(T)-函数.故f就是所求的γr3(T)-函数.

引理2设P=u1u2u3u4u5是树T中的一条路使得d(u1)=d(u5)=1且d(u2)=d(u4)=2,则一定存在一个γr3(T)-函数f使得f(u1)=f(u5)={1},f(u2)=f(u4)=∅且{2,3}⊆f(u3).

证明设h是一个γr3(T)-函数.因为d(u1)=d(u5)=1,所以|h(u1)|+|h(u2)|≥1且|h(u4)|+|h(u5)|≥1.如果|h(u1)|+|h(u2)|=1或|h(u4)|+|h(u5)|=1,则不妨设|h(u1)|+|h(u2)|=1.于是由γr3(T)-函数的定义知,|h(u1)|=1且h(u2)=∅.因此不妨设h(u1)={1}.又因为N(u2)={u1,u3},所以h(u1)∪h(u3)={1,2,3},于是{2,3}⊆h(u3).注意到d(u4)=2且d(u5)=1,因此由γr3(T)-函数的定义知:如果h(u3)={2,3},则h(u4)=∅且h(u5)={1};如果h(u3)={1,2,3},则h(u4)=∅且|h(u5)|=1.于是不妨设h(u5)={1}.故在这种情况下,f=h就是所求的γr3(T)-函数.

如果|h(u1)|+|h(u2)|≥2且|h(u4)|+|h(u5)|≥2,则定义树T的一个3-彩虹控制函数f:V(T)→2{1,2,3}使得f(u1)=f(u5)={1},f(u2)=f(u4)=∅,f(u3)=h(u3)∪{2,3}且当x∉{u1,u2,…,u5}时,f(x)=h(x).于是

γr3(T)≤ω(f)=

ω(h)+(|f(u1)|+|f(u2)|+

|f(u4)|+|f(u5)|)-(|h(u1)|+

|h(u2)|+|h(u4)|+|h(u5)|)+

(|f(u3)|-|h(u3)|)≤

ω(h)+2-4+(|h(u3)∪{2,3}|-

|h(u3)|)≤

ω(h)=

γr3(T)

因此ω(f)=γr3(T).意味着f也是一个γr3(T)-函数.故f就是所求的γr3(T)-函数.

引理3设u1是树T中与叶子点u2和强支撑点u3都相邻的2度弱支撑点,则一定存在一个γr3(T)-函数f使得f(u1)=∅,f(u2)={1},f(u3)={1,2,3}且对任意与u3相邻的叶子点x,f(x)=∅.

γr3(T)≤ω(f)=

ω(h)+4-4=

ω(h)=

γr3(T)

因此ω(f)=γr3(T).意味着f也是一个γr3(T)-函数.故f就是所求的γr3(T)-函数.

引理4如果T=S1,t(t≥3)或T∈Π,则γgr3(T)-γr3(T)=2.

证明首先假设T=S1,t(t≥3).设v1和v2是双星图S1,t的支撑点且设N(v2){v1}={v3}.不难验证,函数f使得f(v1)={1,2,3},f(v3)={1}且当x∉{v1,v3}时,f(x)=∅是一个γr3(T)-函数,并且函数h使得h(v1)=h(v2)={1,2,3}且当x∉{v1,v2}时,h(x)=∅是一个γgr3(T)-函数.因此γgr3(T)-γr3(T)=2.

其次假设T∈Π.设v0是病态蜘蛛树T∈Π的头.令v1和v2是树T的健康脚且对于任意i∈{1,2},令ui是与v0和vi都相邻的弱支撑点.不难验证,函数f使得f(v0)={1,2,3},f(v1)=f(v2)={1}且当x∉{v0,v1,v2}时,f(x)=∅是一个γr3(T)-函数,并且函数h使得h(v0)=h(u1)={1,2,3},h(v2)={1}且当x∉{v0,u1,v2}时,h(x)=∅是一个γgr3(T)-函数.因此γgr3(T)-γr3(T)=2.

命题1设P=v1v2…vk是树T的一条最长路且k≥4.若d(v2)≥3或d(vk-1)≥3,则γgr3(T)-γr3(T)≤2且等式成立当且仅当T=S1,t(t≥3).

证明首先给出以下断言.

断言1如果d(v2)=3或d(vk-1)=3,则γgr3(T)-γr3(T)≤1.

断言1的证明不失一般性,假设d(v2)=3且设N(v2){v1,v3}={u}.令f是一个γr3(T)-函数.注意到v2是度为3的强支撑点,显然有|f(v1)|+|f(v2)|+|f(u)|≥2.

若|f(v1)|+|f(v2)|+|f(u)|=2,则由γr3(T)-函数的定义知,f(v2)=∅,|f(v1)|=|f(u)|=1且f(v1)∪f(v3)∪f(u)={1,2,3}.于是不妨设f(v1)={1},f(u)={2}且3∈f(v3).故不难看出函数h:V(T)→2{1,2,3}使得h(v2)={3}且当x∈V(T){v2}时,h(x)=f(x)是树T的全局3-彩虹控制函数.因此

γgr3(T)≤ω(h)=

ω(f)+|h(v2)|-|f(v2)|=

ω(f)+1=γr3(T)+1

若|f(v1)|+|f(v2)|+|f(u)|≥3,则定义树T的一个全局3-彩虹控制函数h:V(T)→2{1,2,3}使得h(v1)={1},h(u)={2},h(v2)={3},h(v3)=f(v3)∪{3}且当x∈V(T){v1,v2,v3,u}时,h(x)=f(x).于是

γgr3(T)≤ω(h)=

ω(f)+(|h(u)|+|h(v1)|+

|h(v2)|)-(|f(u)|+|f(v1)|+

|f(v2)|)+(|h(v3)|-|f(v3)|)≤

ω(f)+3-3+(|f(v3)∪{3}|-

|f(v3)|)≤

ω(f)+1=

γr3(T)+1

断言1得证.

断言2如果k=4且d(v2)和d(vk-1)中至少有一个不小于4,则γgr3(T)-γr3(T)≤2且等式成立当且仅当T=S1,t(t≥3).

断言2的证明不失一般性,假设d(v2)≥4.因为k=4,所以树T是双星图.如果d(v3)=2,则T=S1,t,其中t=d(v2)-1≥3,于是由引理4知,γgr3(T)-γr3(T)=2.如果d(v3)=3,则由断言1知,γgr3(T)-γr3(T)≤1.如果d(v3)≥4,则函数f:V(T)→2{1,2,3}使得f(v2)=f(v3)={1,2,3}且当x∉{v2,v3}时,f(x)=∅既是一个γr3(T)-函数又是一个γgr3(T)-函数,因此γgr3(T)=γr3(T).断言2得证.

断言3如果k≥5且d(v2)和d(vk-1)中至少有一个不小于4,则γgr3(T)-γr3(T)≤1.

断言3的证明不失一般性,假设d(v2)≥4.注意到v2是至少与3个叶子点相邻的强支撑点,则由引理1,不妨设f是一个γr3(T)-函数使得f(v2)={1,2,3}且对任意x∈N(v2){v3},f(x)=∅.

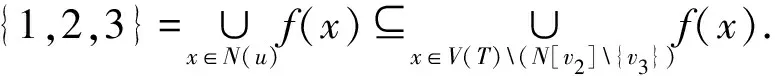
γgr3(T)≤ω(h)=

ω(f)+|h(v3)|-|f(v3)|=

ω(f)+|f(v3)∪{1}|-|f(v3)|≤

ω(f)+1=

γr3(T)+1

如果对任意u∉N[v2],都有f(u)≠∅成立,则函数h:V(T)→2{1,2,3}使得h(v3)=f(v3)∪{1},h(v4)={2},h(v5)={3}且当x∈V(T){v3,v4,v5}时,h(x)=f(x)是树T的全局3-彩虹控制函数,因此

γgr3(T)≤ω(h)=

ω(f)+(|h(v4)|+|h(v5)|)-

(|f(v4)|+|f(v5)|)+

(|h(v3)|-|f(v3)|)≤

ω(f)+2-2+(|f(v3)∪{1}|-

|f(v3)|)≤

ω(f)+1=

γr3(T)+1

断言3得证.

由断言1、2和3知,命题1成立.

命题2设P=v1v2…vk是树T的一条最长路且k≥4.若d(v2)=d(vk-1)=2,则γgr3(T)-γr3(T)≤2且等式成立当且仅当T∈Π.

证明如果k=4,则因为d(v2)=d(v3)=2,所以T=v1v2v3v4是含有4个顶点的路,因此γgr3(T)=4=γr3(T).下面设k≥5.首先给出以下断言.

断言1如果N(v3){v2,v4}=∅,则γgr3(T)-γr3(T)≤1.

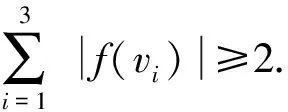
γgr3(T)≤ω(h)=

ω(f)+3-2=

ω(f)+1=

γr3(T)+1

γgr3(T)≤ω(h)=

(|h(v4)|-|f(v4)|)≤

ω(f)+3-3+(|f(v4)∪{3}|-

|f(v4)|)≤

ω(f)+1=

γr3(T)+1

断言1得证.

断言2如果N(v3){v2,v4}中存在一个度至少为2的顶点,则γgr3(T)-γr3(T)≤1.

断言2的证明注意到k≥5.因为P=v1v2…vk是树T的一条最长路且N(v3){v2,v4}中存在一个度至少为2的顶点,所以N(v3){v2,v4}中一定含有树T的强支撑点或弱支撑点.如果N(v3){v2,v4}中存在一个强支撑点,则因为k≥5,所以类似于命题1中断言1和3的证明可得,γgr3(T)-γr3(T)≤1.下面假设N(v3){v2,v4}中存在一个弱支撑点,不妨设为u1.令N(u1){v3}={u2}.由于d(v1)=d(u2)=1且d(v2)=d(u1)=2,则由引理2,不妨设f是一个γr3(T)-函数使得f(v1)=f(u2)={1},f(v2)=f(u1)=∅且{2,3}⊆f(v3).

如果k=5,则因为d(v4)=2,d(v5)=1且{2,3}⊆f(v3),所以由γr3(T)-函数的定义知,f(v4)=∅且|f(v5)|=1,不妨设f(v5)={1};如果k≥6且f(vk-1)和f(vk)都不为∅,则因为d(vk)=1,所以由γr3(T)-函数的定义知,|f(vk)|=1,不妨设f(vk)={1}.于是这两种情况下,不难看出函数h:V(T)→2{1,2,3}使得h(v1)={2},h(v2)={3}且当x∉{v1,v2}时,h(x)=f(x)是树T的全局3-彩虹控制函数.因此

γgr3(T)≤ω(h)=

ω(f)+(|h(v1)|+|h(v2)|)-

(|f(v1)|+|f(v2)|)=

ω(f)+2-1=

γr3(T)+1

下面考虑最后一种情况,即k≥6且f(vk-1)和f(vk)中至少有一个为∅.注意到由γr3(T)-函数的定义知,若f(vk-1)=∅,则f(vk-2)∪f(vk)={1,2,3};若f(vk)=∅,则f(vk-1)={1,2,3}.于是不难验证函数h:V(T)→2{1,2,3}使得h(v4)=f(v4)∪{1}且当x∈V(T){v4}时,h(x)=f(x)是树T的全局3-彩虹控制函数.因此

γgr3(T)≤ω(h)=

ω(f)+|h(v4)|-|f(v4)|=

ω(f)+|f(v4)∪{1}|-|f(v4)|≤

ω(f)+1=

γr3(T)+1

断言2得证.

断言3如果|N(v3){v2,v4}|=1且N(v3){v2,v4}中的顶点为叶子点,则γgr3(T)-γr3(T)≤1.

断言3的证明设N(v3){v2,v4}={u}且设f是一个γr3(T)-函数.由于d(v1)=d(u)=1,则显然有

|f(v1)|+|f(v2)|≥1且|f(v3)|+|f(u)|≥1

(1)

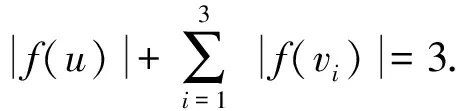
γgr3(T)≤ω(h)=

ω(f)+4-3=

γr3(T)+1

γgr3(T)≤ω(h)=

(|h(v4)|-|f(v4)|)≤

ω(f)+4-4+(|f(v4)∪{3}|-

|f(v4)|)≤

ω(f)+1=

γr3(T)+1

断言3得证.

断言4如果|N(v3){v2,v4}|≥2且N(v3){v2,v4}中的顶点都为叶子点,则γgr3(T)-γr3(T)≤2且等式成立当且仅当T∈Π.

断言4的证明注意到k≥5.首先假设k=5.若|N(v3){v2,v4}|=2,则不妨设N(v3){v2,v4}={u1,u2}.又因为d(v2)=d(v4)=2,所以V(T)={v1,v2,v3,v4,v5,u1,u2}.于是函数f使得f(v1)=f(v5)={1},f(v3)={1,2,3}且当x∉{v1,v3,v5}时,f(x)=∅是一个γr3(T)-函数,并且函数h使得h(v1)=h(v5)={1},h(v2)=h(v4)=∅,h(v3)={2,3},h(u1)={2}且h(u2)={3}是一个γgr3(T)-函数.因此γgr3(T)-γr3(T)=6-5=1.若|N(v3){v2,v4}|≥3,则T∈Π,于是由引理4知,γgr3(T)-γr3(T)=2.

其次假设k≥6.如果N(vk-2){vk-3,vk-1}=∅,则类似于断言1的证明可得γgr3(T)-γr3(T)≤1.如果N(vk-2){vk-3,vk-1}中存在度至少为2的顶点,则类似于断言2的证明可得γgr3(T)-γr3(T)≤1.如果|N(vk-2){vk-3,vk-1}|=1且N(vk-2){vk-3,vk-1}中的顶点为叶子点,则类似于断言3的证明可得γgr3(T)-γr3(T)≤1.下设|N(vk-2){vk-3,vk-1}|≥2且N(vk-2){vk-3,vk-1}中的顶点都为叶子点.

由于N(v2)={v1,v3}且v1和v3分别是叶子点和强支撑点,则由引理3,不妨设f是一个γr3(T)-函数使得f(v1)={1},f(v2)=∅,f(v3)={1,2,3}且对任意x∈N(v3){v2,v4},f(x)=∅.由于d(vk-1)=2,d(vk)=1且vk-2是强支撑点,则再次由引理3,不妨设f(vk)={1},f(vk-1)=∅,f(vk-2)={1,2,3}且对任意x∈N(vk-2){vk-3,vk-1},f(x)=∅.于是不难看出函数h:V(T)→2{1,2,3}使得h(v1)={2},h(v2)={3}且当x∉{v1,v2}时,h(x)=f(x)是树T的全局3-彩虹控制函数,因此

γgr3(T)≤ω(h)=

ω(f)+(|h(v1)|+|h(v2)|)-

(|f(v1)|+|f(v2)|)=

ω(f)+2-1=

γr3(T)+1

断言4得证.

由断言1～4可知,命题2成立.

定理1对任意树T,下列结论成立:

(1)γgr3(T)-γr3(T)=2当且仅当T∈{K1,4,S1,t(t≥3)}∪Π.

(2)γgr3(T)-γr3(T)=3当且仅当T=K1,n-1(n≥6).

证明设树T含有n个顶点.如果n≤3,则易见γgr3(T)=n=γr3(T).下面设n≥4.如果树T的直径为2,即T=K1,n-1,则当n=4时,γgr3(T)-γr3(T)=4-3=1;当n=5时,γgr3(T)-γr3(T)=5-3=2;当n≥6时,γgr3(T)-γr3(T)=6-3=3.如果树T的直径至少为3,则由命题1和2知,γgr3(T)-γr3(T)≤2且等式成立当且仅当T=S1,t(t≥3)或T∈Π.定理1得证.

3 结 语

本文研究了图的经典控制数的一个衍生控制参数,即全局彩虹控制数问题.通过对树的结构分析,刻画了γgr3(T)-γr3(T)=2和γgr3(T)-γr3(T)=3成立的所有树T,推广了已知结果.期望在今后的研究工作中能够进一步刻画γgr3(T)-γr3(T)=1成立的所有树T.