一维输运方程的编程求解及可视化

黄海深，万秋红，李 平，周庭艳，吴 波

（遵义师范学院 物理与电子科学学院，贵州 遵义)

引言

数学物理方法是物理学本科班的专业必修课程，按照人才培养方案设计的理念，重点加强对学生自学能力的培养，学生应当掌握课程中的复变函数论和数学物理方程的基础知识、基本研究方法和思想，并能够在今后的学习和实践中加以应用。

数学物理方法是以研究物理问题为目标的数学理论和数学方法，对物理现象建立数学模型，寻求物理现象的数学描述和诠释。数学物理方法主要包括复变函数论、特殊函数论和数学物理方程等内容，涉及到许多偏微分方程和特殊方程。数学物理方法以普通物理和高等数学为基础，内容具有“繁、杂、难”的特点，加上学生基础薄弱，学生学习起来比较困难，成为学生眼中的“天书”，造成学习主动性不高，学习效果较差[1]。

计算科学的发展和计算机处理能力的大幅提升，为数学物理中的许多问题提供了另一个解决思路，并发展出了一个新的学科，即计算物理学。计算物理学是以计算机技术为工具和手段，运用数学方法解决复杂物理问题的一门应用科学，它是计算机科学、数学和物理学相结合的学科。目前计算物理已经成为对复杂体系的物理规律、物理性质进行研究的重要手段，是物理学的重要分支之一，与理论物理和实验物理有着密切的关系，对物理学的发展起着越来越大的作用。

计算物理首先对复杂物理问题建立物理模型，然后用数学理论导出方程，最后利用数值计算方法来求解和仿真，可以很直观地对问题进行分析，因此计算物理在数学物理方法课程的许多章节中发挥作用。本文以一维输运方程为例，研究有限差分方法在偏微分方程的数值求解和可视化方面的应用，为建立数学物理方法课程的数值求解及可视化资源库打下基础。

1 输运方程的建立

当物体的温度不均匀时，热量就会从温度高的地方向温度低的地方转移，这种热传导现象遵从热传导定律，即傅里叶定律：

式中：u 为温度，它是位置r 和时间t 的函数；∇u为温度的梯度，表示u 的不均匀程度；q 为单位时间内流过单位横截面积的热量，即热流密度，比例系数k 为热传导系数。

根据热传导定律及能量守恒定律，可推导出物体的温度满足以下偏微分方程[2]：

当物质的浓度不均匀时，物质的扩散现象也遵循与傅里叶定律相似的扩散定律，即斐克定律，因此热传导方程和物质的扩散方程具有相同的形式：

此类方程即输运方程。为简单起见，本文只考虑比较简单的一维的情况，即：

2 输运方程的求解

对于齐次输运方程，如果边界条件也是齐次的，一般可用分离变量方法进行求解。例如对于定解问题：

式(5)化为

关于x 部分的解已经求出，将本征值代入式(11)可得：

此为关于t 部分的解。考虑初始条件式(8)后，可求出定解问题的解为[3]：

此题的初始条件是三角函数，而且正好为式(11)的本征函数，所以最后求解特解时相对容易些，如果不是本征函数，则需要采用傅里叶变换求解展开系数，求解过程则更为复杂。对于一般的输运方程，求解过程是非常复杂的，甚至求不出解析解。因此，接下来我们采用有限差分方法求输运方程的数值解并对数值进行可视化。

3 数值求解及可视化

有限差分方法是求解偏微分方程的一种常用方法，它使用差商代替偏微分方程中的偏导数，这样偏微分方程就变成了代数方程，连续方程实现了离散化，再联合边界条件和初值条件即可求解出方程的数值解。

下面是采用有限差分方法对一维输运方程进行数值求解并进行可视化。解为u(x,t)=ex+t输运方程为：

选用此方程的目的是其解析解已知，方便评估我们的求解方法和过程的可靠性。

则式(20-23)可离散为[4]

至此通过C++或其他语言编程可很方便地求解出数值解，将数值导入到作图软件中即可画出函数图像，对输运方程的解进行可视化。例如取M=50、N=5000 时，图像如图1 所示。由图1 可以直观地看出，函数值随时间是增加的，其原因是边界处函数值是随时间增加的，相当于两端有两个热源不断地对体系进行加热，所以温度一直在上升。

图1 M=50、N=5000 时式(20-23)的图像

有限差分方法是使用有限大小的间隔对求解区域时行划分，并用差商代替偏导数，因此迭代的次数越多，误差越大，即时间越长，误差越大，如图2 所示。在本例中，t=1 时最大的误差在x=0.5 附近，约为3.48×10-5，边界处的值已知，误差为0。除了迭代次数，误差还与网格大小相关，网格划分得越细，误差越小。但也不是越细越好。网格越细，计算的数据越多，处理起来越困难。而且许多作图软件能处理的精度有限，过高的精度并不能体现出来。

图2 M=50、N=5000、t=1 时，采用有限差分方法求解式(20-23)的误差图像

对于式(5-8)的定解问题，取D=1，M=90，N=5000，图像如图3 所示。由图3 看出，函数值随时间衰减得很快，t=1 时，最大值已经衰减到10-11的数量级。由边界条件可知边界的值固定为0，对于热传导问题相当于两端有温度为0 的热浴，经过一段很短的时间，体系的温度将接近热浴的温度，即趋于0。

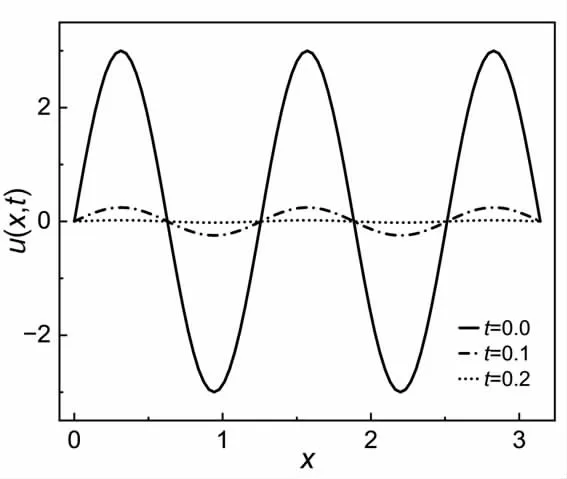
图3 M=90、N=5000、D=1 时，式(5-8)的图像

再看一个齐次方程的例子：

初始条件为0，边界条件为关于t 的正弦函数，两端的符号相反。此方程的边界条件是非齐次的，求解非常麻烦，采用有限差分方法求出数值解，由origin 软件画出的函数图像如图4 所示。由图4 可以看出，两端都以正弦函数变化，向中间输运。因两端符号相反，造成x＜0.5 时函数始终大于0，x＞0.5 时函数始终小于0，而x=0.5 时函数始终为0。从图中可以看出，输运方程与波动方程的图像有着本质区别，后者的图像遵循叠加原理，而前者不遵循叠加原理，而会相互抵消。

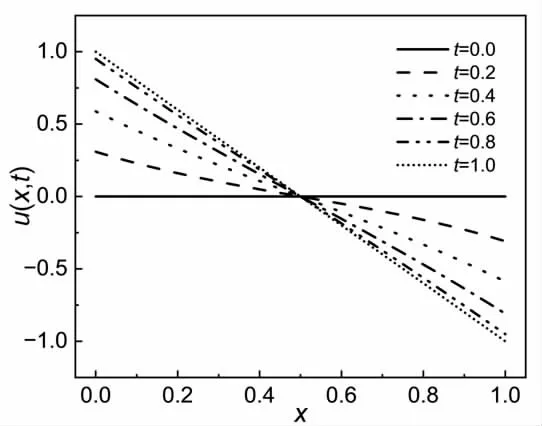
图4 M=50、N=5000 时，式(31-34)的图像

4 结论

本文首先简单介绍了一维输运方程的建立和基于分离变量法的解析解求解方法，然后采用有限差分方法对一维输运方程进行了离散化处理，最后经过编程求出了两个定解问题的数值解，并进行了可视化。该方法一旦编程成功，改变边界条件和初始条件也可很方便地求解出方程的数值解并进行画图。该方法可移植性较高，直观性较强，可降低学生学习输运方程的难度，提高其学习兴趣。