基于伺服电机驱动的进给传动系统扭转振动的Lie 群分析方法1)

徐 宏 傅景礼

(山东外事职业大学信息与控制工程学院,山东威海 264500)

引言

伺服驱动的数控机床中,进给系统的定位精度高低决定了零部件的加工精度、表面质量[1-3],且进给动作进行时,其运动平稳性还直接影响机床的刀具寿命,故现代加工与制造业对进给传动系统有更高的速度与定位精度要求[4-5],以使数控设备具有更高性能.激光切割机具有典型的进给传动系统在校准后能够保证加工精度,但是,一段时间过后,其精度无法满足加工需要.若重新校准需要大量的工作步骤,使激光切割机的加工效率大大降低,还会带来成本问题[6-8].因此,本文对激光切割机伺服电机驱动的滚珠丝杠进给传动系统进行动力学建模,研究其动态特性,成为有效地降低及控制伺服电机驱动的进给过程中扭转振动的关键技术.

分析力学选择坐标,基于理想约束的概念,从能量的角度提出动力学系统的基本原理,建立系统的动力学方程,适合解决质点系和多刚体系统的机械装置的复杂问题[9],在约束力学系统和机械动力系统的建模方面得到广泛应用[10-11].通过构造系统的Lagrange 函数,写出其Lagrange 方程,从能量的角度建立系统的运动方程Lagrange 方程[12-13].1918 年Noether 提出了著名的Noether 定理,描述了动力学系统的某种对称性和守恒量之间一一对应的关系.近年来,Noether 对称性已被推广应用到多种约束力学系统(例如非保守系统、非完整系统、Birkhoff 系统和机电耦合系统等)中[9,14-21],理论趋于完善.事实上,不论是机械系统、机电耦合系统还是一般电路系统,都可用Noether 对称性理论得到系统的解[22-24].

本文将Noether 对称性理论应用于激光切割机伺服电机驱动的滚珠丝杆传动系统扭转振动问题.给出该系统的动能、势能和Lagrange 函数;建立该系统的第二类Lagrange 方程和约束方程;引入关于时间和广义坐标的变换Lie 群,给出该系统的Noether定理和守恒量;利用得到的守恒量给出激光切割机传动系统的动态响应,并对动态响应进行数值模拟.

1 激光切割机进给传动系统扭转振动的模型及其动力学方程

本文以具有3 个方向自由度的激光切割机为研究对象,如图1 所示的激光切割机是由直线模组搭建的示意图.该切割机以X,Y,Z轴三分方向进行进给传动运动,各轴传动均采用滚珠丝杠进行动作[25],并且X,Y,Z轴均由伺服电机进行驱动,表1 列出了以江苏亚威机床股份有限公司生产的HLH2040 激光切割机为研究对象的技术参数.

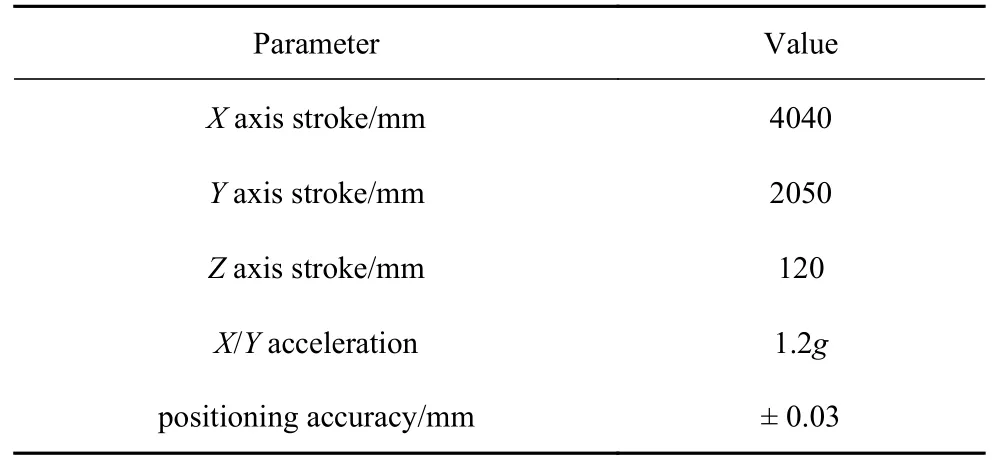
表1 HLH2040 激光切割机技术参数Table 1 Technical parameters of HLH2040 laser cutting machine

图1 激光切割机示意图Fig.1 Schematic of a laser cutting machine

下面给出激光切割机的进给传动系统主要部件的组成示意图,如图2 所示.在传动进给过程当中,轴向载荷引起该系统的轴向变形和振动,在此振动过程中,可等效为激光切割机滚珠丝杠和伺服电机系统发生的振动位移[26].

图2 进给系统示意图Fig.2 Schematic of feed drive system

本文将带负载沿X轴方向一侧的传动系统作为研究对象.因激光切割机在传动进给过程中沿该方向的移动运行次数是最多的,且负载相对较大,运行速度相对较快,故此方向传动系统动态特性对激光切割机在运行过程中的定位精度影响最大[27].

现对滚珠丝杠进给系统的轴向进行集中质量建模,滚珠丝杠传动系统的2 个自由度将被保留.滚珠丝杠进给系统简化后的等效轴向振动模型如图3 所示.

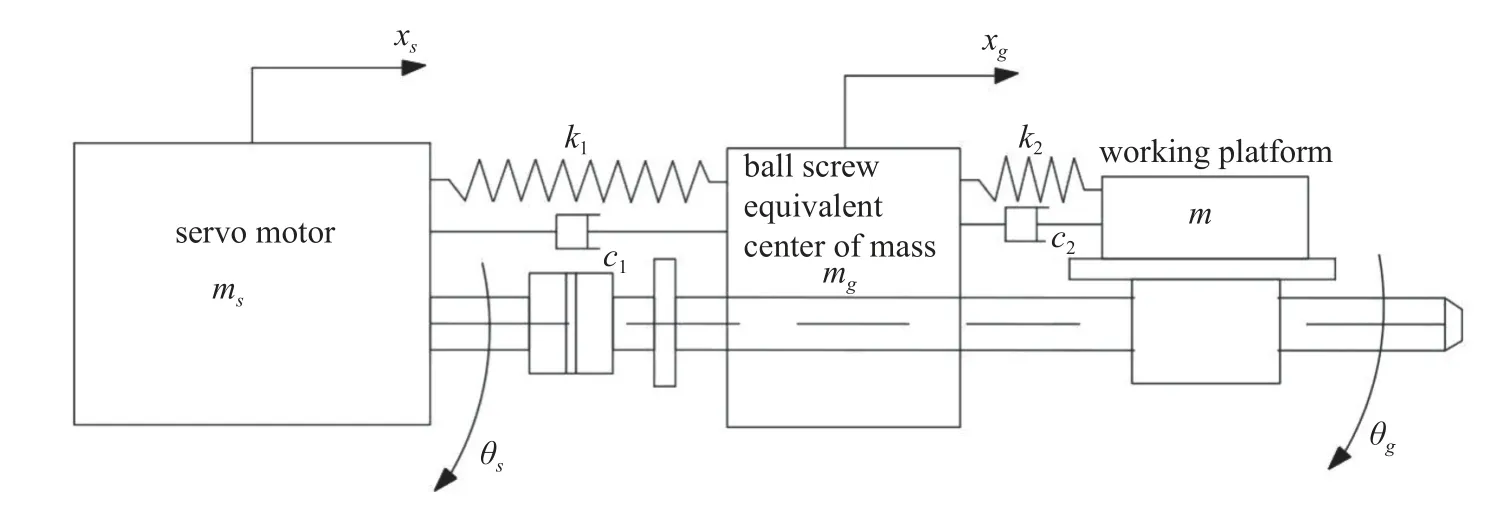
图3 进给系统等效轴向振动模型Fig.3 Equivalent axial vibration model of feed system

一般机电系统Lagrange 方程[28]为

式中,zs,qs为系统相互独立的机械与电气广义坐标,D为耗散函数,Qs和Ek为对应广义坐标的广义力和电源电压,Λs为非完整约束力.其中

λβ为约束乘子,系统的非完整约束为

在简化动力学模型中,假设激光切割机作X轴方向一侧的传动进给产生振动.系统中等效的伺服电机质量ms、滚珠丝杠质量为mg,伺服电机驱动位移xs、滚珠丝杠的位移xg,滚珠丝杠转动惯量为Jg,伺服电机转动惯量为Js,θs和 θg分别是伺服电机和滚珠丝杠的转动角度,k1和k2为伺服电机和滚珠丝杠的等效刚度.c1和c2是伺服电机和滚珠丝杠的等效阻尼,系统中的耗散函数为

故xs与xg为广义坐标,则激光切割机进给系统扭转振动的动能为

不计激光切割机在传动进给过程负载重量的影响,势能为存储于变形的弹簧中的势能,则

假设伺服电机与滚珠丝杠转动的角度与位移之间的系数为E1与E2,有如下的约束关系

那么,此系统存在非完整约束.

故系统的Lagrange 函数可表示为

因激光切割机床的激光器不直接与工件接触,在加工过程中,没有外力的作用,系统广义坐标对应的广义力为Qs=0.考虑系统耗散公式D,将式L方程和广义力方程代入一般Lagrange 方程,可以得到系统运动微分方程为

2 激光切割机进给传动系统扭转振动的Noether 对称性与守恒量

引进群关于时间、坐标的无限小变换[29]

其中,ε 为无限小参数,ξ0,ξ1,ξ2为无限小变换的生成元.

引入激光切割机进给传动系统扭转振动Hamilton作用量[30],若γ 表示某曲线,则

在变换式(11)下,曲线γ 将变为γ*,那么此时系统的Hamilton 作用量表示为

作用量S的变分 ΔS为S(γ*)-S(γ) 的相对 ε 的主线性部分,有

将无线小变换代入变分公式,并注意到

式(16)和式(18)为该系统Hamilton 作用量变分的基本公式.

定义1如果激光切割机进给传动系统扭转振动的Hamilton 作用量是无限小变换下的不变量,即无限小变换满足

则无限小变换是完整激光切割机进给传动系统的Noether 对称性变换.

定义2如果系统Hamilton 作用量是无限小群变换的广义准不变量,即对每一个无限小变换,始终存在

其中,G为规范函数,Q1和Q2为广义力,本系统中的两个广义力为0,Λ1和 Λ2表示广义非完整约束力,则称变换式(11)为系统广义准对称变换.

由上述定义公式(19)和系统 Hamilton 作用量变分的基本公式可以得到完整系统的如下判据1:对于无限小群变换式(11),若满足条件

则变换式(11)为完整激光切割机进给传动系统扭转振动的Noether 对称性变换.

由于 ε 独立性可以得到完整激光切割机进给传动系统扭转振动的Noether 恒等式

Noether 定理 1:假设无限小变换式 (11) 是完整激光切割机进给传动系统扭转振动的 Noether 对称变换,则该系统存在如下形式的守恒量

Noether 定理 1 也可以表示为 Noether 定理2.

Noether 定理 2:对于完整激光切割机进给传动系统扭转振动,若无限小变换式 (11)满足Noether恒等式 (22),则完整激光切割机进给传动扭转振动系统存在守恒量(23).

用定义公式 (20) 和系统 Hamilton 作用量变分的基本公式可以得到保守非完整激光切割机进给传动系统扭转振动相应保守完整激光切割机进给传系统动扭转振动广义Noether 准对称性的如下判据2:对于无限小群变换式(11),若满足条件

则变换式(11)是保守非完整激光切割机进给传动系统扭转振动相应保守完整激光切割机进给传动系统扭转振动的广义 Noether 准对称变换.

由于 ε 独立性,可以得到保守非完整激光切割机进给传动系统扭转振动相应保守完整激光切割机进给传动系统扭转振动的Noether 恒等式

Noether 定理 3:若存在规范函数G,使得无限小变换式(11)是保守非完整激光切割机进给传动系统扭转振动相应保守完整激光切割机进给传动系统扭转振动广义Noether 准对称变换,则该系统存在如下形式的守恒量

Noether 定理 3 也可以表示为: 对于保守非完整激光切割机进给传动系统扭转振动相应保守完整激光切割机进给传动扭转振动系统,如果存在规范函数G使得无限小变换式 (11) 满足Noether 恒等式(25),则该系统存在守恒量 (26).

定义3如果无限小变换式(11)是保守非完整广义 Noether 准对称性变换,且变换还满足条件

则称变换式 (11) 是保守非完整激光切割机进给传动系统扭转振动的强广义 Noether 准对称变换.

Noether 定理 4:如果存在规范函数使得无限小变换式 (11) 是保守非完整激光切割机进给传动系统扭转振动的强广义 Noether 准对称变换,则该系统存在守恒量 (26).

当条件(27)放宽为以下条件

便可以得出激光切割机进给传动系统扭转振动的弱广义 Noether 准对称变换.

Noether 定理 5:如果存在规范函数使得无限小变换式 (11) 是保守非完整激光切割机进给传动系统扭转振动的弱广义 Noether 准对称变换,则该系统存在守恒量 (26).

由 Noether 守恒量 (26) 再给定初始条件便可得出保守非完整激光切割机进给传动系统扭转振动相应保守完整激光切割机进给传动系统扭转振动在进给过程中的运动规律.

对于该振动系统,如果存在规范函数G=G(t,xs,,xg,),那么系统的Noether 等式

Noether 等式可以写成Killing 方程的形式

将系统的Lagrange 方程代入广义Killing 方程,得到以下3 个方程

设生成函数有下面的形式

将G和生成函数代入Killing 方程式(30)得

将等式两边相同项系数整理出来,得

经计算,可得

生成元可表示为

当s0,s1,s2取特殊值时,可以得到以下几种对称性

由激光切割机进给传动系统扭转振动的Noether定理形如下

代入系统的Lagrange 函数可以得到以下守恒量

我们观察到守恒量I3=0,显然这是平庸的;I1=-I2,说明它们不是相互独立的;且I1,I2,I4和I5是系统的能量积分.如果有足够的守恒量,守恒量就可以用于求运动方程的精确解,同时可以用于对方程求数值解.

3 激光切割机传动系统扭转振动的动态响应

激光切割机传动系统扭转振动的守恒量以及对称性解的计算可以借助MATLAB 软件,通过它可以编写程序绘制相应的动态曲线[31].HLH2040 激光切割机加工范围是4000 mm×2000 mm,工作台最大载重1500 kg,其加、减速初始阶段会有机床振动现象产生[32],在0～0.2 s 时间段内应用前文研究的守恒量.

激光切割机启动的初始值设定为0

系统中各技术参数列于表2.

表2 技术参数Table 2 Technical parameters

伺服电机选择额定容量为1.5 kW 的电机模型,转动扭矩约为9.5 N·M

根据得到的守恒量、系统的动力学方程可以求得系统的响应方程

代入初始值可得到如图4 和图5 所示的动态响应.

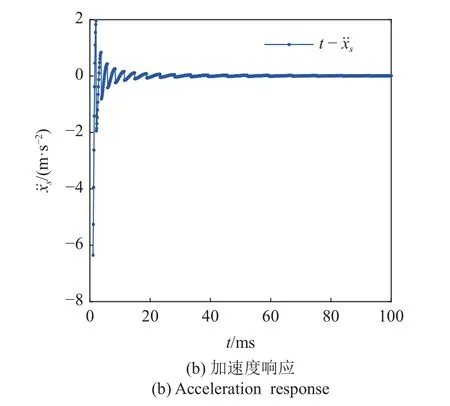
图4 伺服电机的速度和加速度响应Fig.4 The velocity response and acceleration response of the servo motor

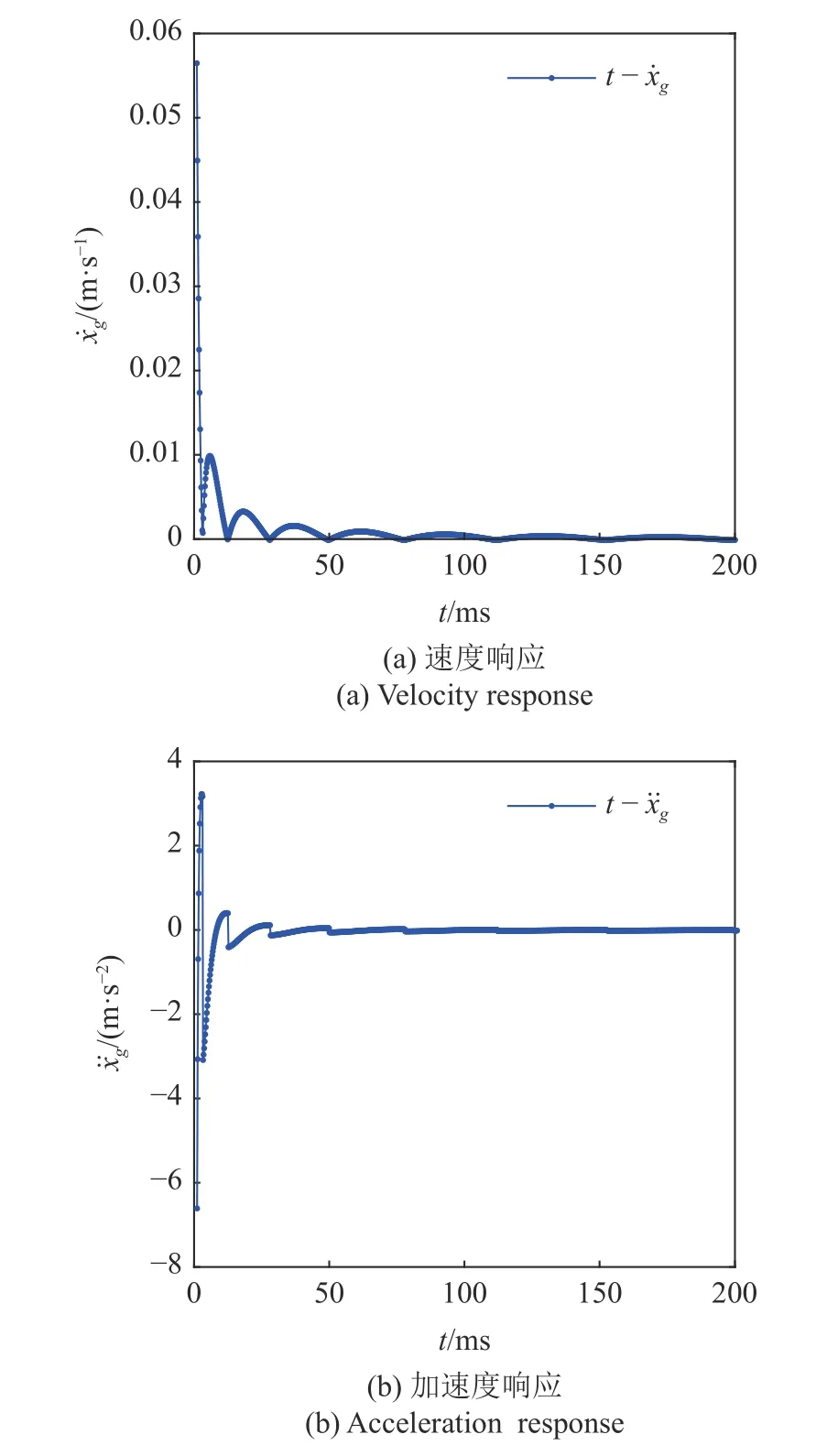
图5 滚珠丝杆的速度和加速度响应Fig.5 The velocity response and acceleration response of the ball screw

图4(a)和图4(b)为伺服电机的速度响应和加速度响应,从这两张图可以看出,在启动瞬间随着时间的推移,系统趋于稳定运行,本文所用的对称性方法的加入使得系统能够在极短的时间,约10 ms 的时间,即迅速稳定.

图5(a)和图5(b)为滚珠丝杆的速度响应和加速度响应,从这两张图可以看出,在启动瞬间随着时间的推移,系统趋于稳定运行,同样使用分析力学Noether 对称性方法约10 ms 的时间,系统快速趋于稳定.

4 结论

本文将Lie 群理论应用于伺服电机驱动的进给传动系统扭转振动问题,研究了两自由度非完整保守激光切割机进给传动系统的扭转振动现象.首先,根据现有的一般机电系统模型,结合扭转振动的力学模型,给出了机械动力学模型.其次,引入关于时间和坐标的无穷小变换,描述激光切割机进给驱动系统扭转振动的Hamilton 作用,并给出扭转振动的相关定义,从而给出其相应的Noether 定理.

然后,根据给出的定理,求出激光切割机进给传动系统扭转振动的守恒量.最后,将守恒量与扭转振动的机械动力学方程相结合,得到系统的对称解,并利用 MATLAB 软件进行数值模拟.此外,本文给出的Lie 群分析方法还可应用于其他复杂的机械振动系统.