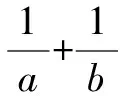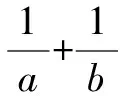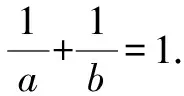有关基本不等式的常见题型
安徽省涡阳第一中学 李友转
1 直接应用类[1]
此类问题直接利用基本不等式求最值即可.注意“一正、二定、三相等”这三个条件缺一不可.
例1已知0 分析:满足“一正、二定、三相等”这三个条件,可以直接利用基本不等式求解. 解析:由0 由基本不等式,可得 例2(2015年天津高考·文)已知a>0,b>0,ab=8,则当a的值为______时,log2a·log2(2b)取得最大值. 分析:本题结合对数知识考查基本不等式的应用,满足“一正、二定、三相等”这三个条件,直接利用基本不等式反解出参数的值. 又a>0,b>0,ab=8,所以a=4,b=2. 此类问题一般不能直接使用基本不等式,要从整体上把握式子的结构特征,对不满足使用基本不等式条件的式子通过“变形”来转换,但不论怎么变形,都需要根据条件转化成凑和为定值时求积最大,或凑积为定值求和最小. 因为t>0,所以利用基本不等式可得 故所求最小值为-2. 分析:题目要求和的最小值,就要配凑积为定值,所以要减去2,再加上2,保持原式不变,进而利用基本不等式求解. 由x>2,得x-2>0. 因此所求最小值为4. 分析:本题中函数解析式为一个分式,不利于求出最小值,所以可通过分离常数,凑出积为定值的式子,再利用基本不等式求解. 分析:要求积的最大值,就要配凑出和为定值的式子,再利用基本不等式求解. 因此,利用基本不等式可得 在求解含有两个变量的代数式的最值问题时,常通过变量替换或换“1”法[3]来构造基本不等式求解. 分析:利用换“1”法,出现积为定值的式子,进而利用基本不等式来求和的最小值. 解析:由a>0,b>0,a+b=1,可得 因此,利用基本不等式可得 例8若正数x,y满足x+3y=5xy,则3x+4y的最小值是______. 解析:由x>0,y>0,x+3y=5xy,可得 所以,对所求式子进行整体代换,得 利用基本不等式,可得 故所求最小值为5. A.2 B.3 C.4 D.5 分析:本题借助直线背景考查基本不等式的应用,简单利用换“1”法即可求解. 又a>0,b>0,所以 当且仅当a=b=2时,等号成立. 故所求最小值为4. 解决基本不等式的相关题型,首先要掌握利用基本不等式求最值时的前提,即:(1)非零的各数(或式)均为正;(2)和或积为定值;(3)等号能否成立.这三个条件缺一不可. 其次就是辨别所求式子的类型,根据已知条件用相应的方法解题即可.


2 恒等变形类[2]
2.1 拆项法
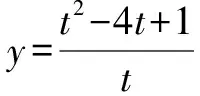
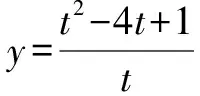
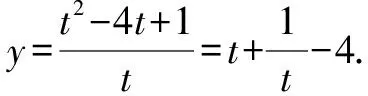

2.2 凑项法
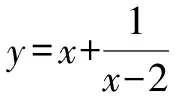
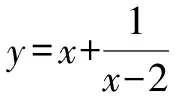

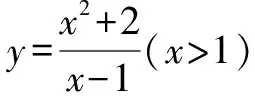
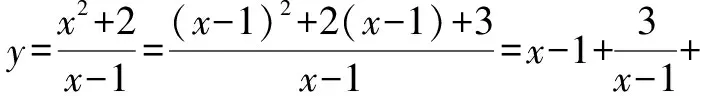
2.3 凑系数法

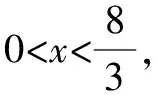
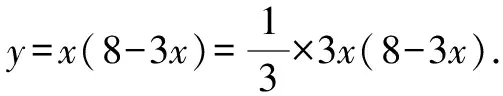
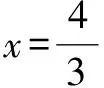
3 条件最值类