剖析解三角形问题,发展关键能力——基于2022年高考解三角形类解答题的考查

江苏省苏州市张家港市张家港高级中学 蔡怡欢

解三角形是高中数学的重要内容之一,合理联系初中的平面几何,链接高中的三角函数与平面向量知识,是高中数学中比较特殊的一个知识点,也是历年高考考查的重点之一.解三角形通常出现在高考试卷解答题中,位置偏前,难度中等.其中,三角形边或角等元素的求值,边或角关系式的证明,与其他相关知识的抽象与交汇以及创新应用或实际应用等方面,都是很好的考查方向.

1 通过求值,考查数学运算

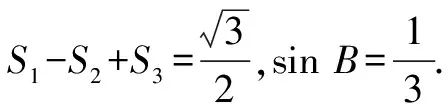
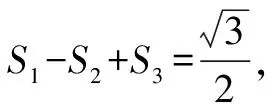
点评：通过三角形的创设,结合边或角的相关代数式以及关系,求解具体角的大小、具体边的长度、三角形的面积或对应代数式的值等,一直是高考中最常见的解三角形解答题的设置方式与考查方式,关键是综合三角函数的相关公式、解三角形的相关公式及平面几何知识来化归转化,进而通过数学运算求解.

2 通过证明,考查逻辑推理

例2(2022年高考数学全国乙卷理科·17)记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A-B)=sinBsin(C-A).

(1)证明:2a2=b2+c2;

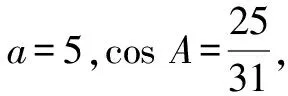
(1)证明：在△ABC中,由sinCsin(A-B)=sinBsin(C-A),得sinC(sinAcosB-cosAsinB)=sinB(sinCcosA-cosCsinA),整理有sinA·(sinBcosC+cosBsinC)=2cosAsinBsinC.

所以sinAsin(B+C)=sin2A=2cosAsinBsinC,结合正弦定理,可得a2=2bccosA.

由余弦定理,可得a2=b2+c2-2bccosA,所以2a2=b2+c2.

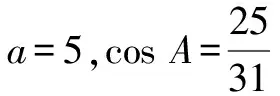
所以△ABC的周长为a+b+c=5+9=14.

点评：解三角形问题中边或角关系的转化,涉及三角函数公式以及解三角形中的正(余)弦定理等,利用条件与结论之间的联系,合理通过逻辑推理与数学运算求解.

3 通过转化,考查数学抽象

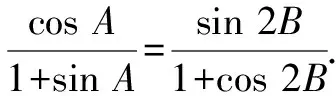
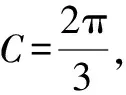
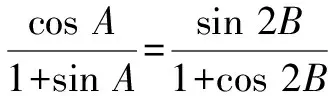
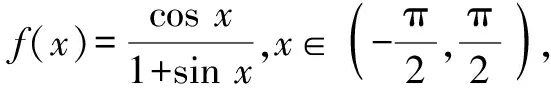
点评：以解三角形为问题背景,交汇解三角形与三角函数、函数、不等式等相关知识,数学抽象,合理转化,借助三角函数关系式的同构与应用,合理构建角之间的关系,是破解此类问题的关键所在.等价转化并加以数学抽象,回归数学本质,是此类考题的亮点.

4 通过探究,考查数学建模

例4(2022年高考数学上海卷·19)如图1所示,AD=BC=6,AB=20,O为AB中点,曲线CMD上任一点到点O的距离相等,∠DAB=∠ABC=120°,MO⊥AB,点P,Q关于OM对称.

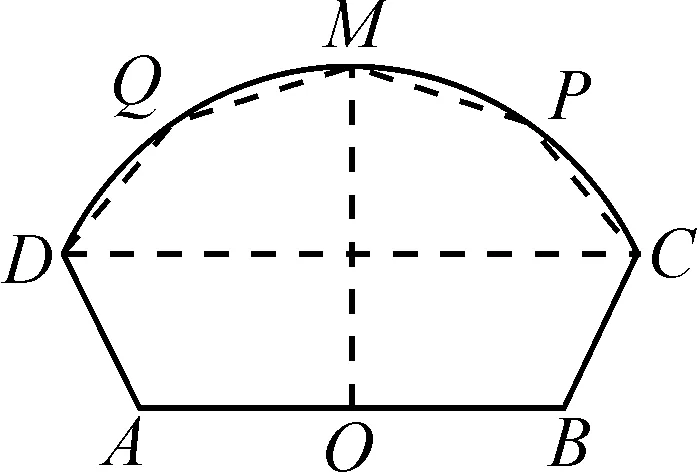
图1

(1)若点P与点C重合,求∠POB的大小;

(2)求五边形CDQMP面积S的最大值.

解析：(1)若点P与点C重合,由题意可得OB=10,BC=6,∠ABC=120°.

范坚强停下车，远远地看着傻姑。她在一个肮脏的世界里寻找，寻找食物，寻找乐趣，寻找寻找本身。此时，傻姑在一棵树下，盯着三毛快餐店热气腾腾的包子出神。她呆呆地看着一个个顾客走过来，停在店前，三毛抱开蒸屉，熟练地夹起雪白的包子装进塑料袋，一手接钱一手将包子递给顾客。傻姑咬着手指看着，唾液在嘴角断断续续地牵出一条细丝。

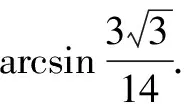
(2)如图2,设CD与MO相交于点N,由题意知五边形CDQMP关于MN对称.

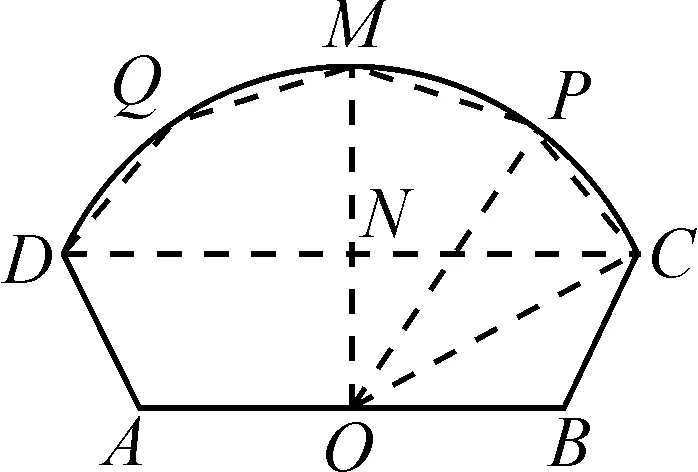
图2

所以,可得S五边形CDQMP=2S四边形CPMN=2(S四边形OCPM-S△ONC).

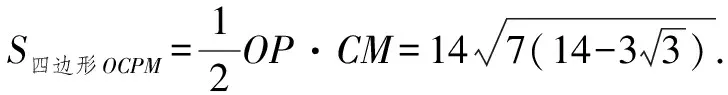
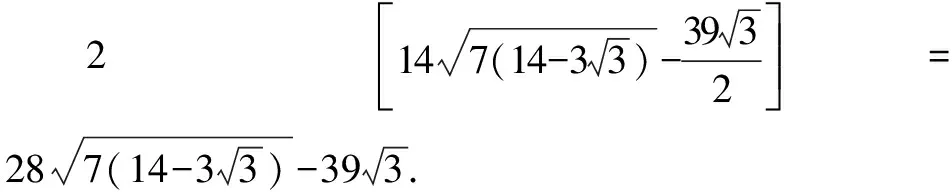
同理,当P为劣弧DM中点时,S也取得相同的最大值.

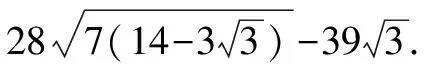
点评：此题借助扇形的性质、正弦定理与余弦定理及三角形的面积公式在解三角形问题中的应用,合理创设情境,结合点的位置的确定以及对应的面积的最值来合理综合应用,考查了逻辑推理、数学运算等能力.借助解三角形的创新情境来解决一些相应的实际应用问题,也是解三角形综合应用的途径.

解三角形解答题的场景离不开平面几何,借助几何场景合理构建数学模型,利用三角公式进行逻辑推理,结合三角形知识巧妙代数运算、综合探究、创新应用等,考查考生数学基础知识、基本技能、基本思想、基本活动经验等方面的落实情况,引领高中数学教学与学习.