基于稀疏贝叶斯学习的大规模多用户检测算法

陈平平，王宣达，谢肇鹏，方毅，陈家辉

（1.福州大学先进制造学院，福建 泉州 362251；2.福建省媒体信息智能处理与无线传输重点实验室，福建 福州 350108；3.广东工业大学信息工程学院，广东 广州 510006）

0 引言

5G 海量机器类通信（mMTC,massive machine type communication）场景如今受到广泛关注，并被应用于工业自动化、自动驾驶、智慧城市等物联网领域。在mMTC 通信场景下，传统的基于调度的正交多址接入方案已经无法满足需求。由于基站要为每台设备分配正交的时间或频率资源，当设备的总数远多于资源的总数时，复杂的调度过程会导致显著信令开销和过多时延[1]，这在发送零星短数据包的场景中效率很低。为了克服上述缺点，研究者提出一种免授权非正交多址接入（GF-NOMA,grant-free non-orthogonal multiple access）方案，允许设备在相同的时间或频率资源上传输数据符号而不需要依赖基站授权[2-3]。用户在传输过程中不需要基站的上行授权，而是随机自主地传输数据，因此基站并没有来自用户的任何先验信息，需要进行多用户检测，在接收到信号后能够识别所有发送信息的活跃用户集合，从而检测出它们发送的数据。

在mMTC 传输场景中，活跃用户数一般远少于总用户数，即活跃用户是稀疏的，这就使原先的多用户检测问题能够转换为稀疏信号的重构问题。传统的压缩感知算法，如正交匹配追踪[4]、分段正交匹配追踪[5]等经典贪婪算法已经被广泛应用。Wang 等[6]利用mMTC 系统中活跃用户固有结构稀疏性提出一种结构化迭代支持检测算法，能够在连续的时隙中联合检测活跃用户和其传输的数据。利用前一时隙估计的传输符号和活跃用户集作为先验知识，一种交替方向乘子法算法可以提高多用户检测性能[7]。文献[8-9]研究了基于期望传播的联合活跃用户检测、信道估计和数据检测的方法。通过改进识别序列，将正弦扩频序列应用于mMTC 的扩频序列，一种非迭代、低复杂度的算法被用于多用户检测[10]。

然而，上述方法得出的往往不是最优的稀疏解，贝叶斯算法证明在多数情况可以实现最优的稀疏解。Tipping 等[11]提出了一种稀疏贝叶斯学习（SBL,sparse Bayesian learning）算法，用于机器学习中的回归和分类。Wipf 等[12-13]将SBL 算法引入压缩感知（CS,compressive sensing）领域，针对单测量向量（SMV,single measurement vector）模型稀疏信号进行恢复，并扩展到多测量向量（MMV,multiple measurement vector）模型推导出MSBL（multiple SBL）算法。Zhang 等[14]研究了块稀疏贝叶斯学习框架，将MMV 模型转化为具有块状结构的SMV 模型，探索时间相关性进而提出了T-SBL和T-MSBL 算法。Fang 等[15]则提出了支撑集辅助的稀疏贝叶斯学习算法，应用一部分已知的先验支撑集信息，在参数上增加了第三层先验，表征稀疏控制的超参数。Fang 等[16]研究了结构化配对的稀疏贝叶斯学习算法，将每个单独的超参数与每个系数独立关联，而每个系数不仅涉及其自身的超参数，还涉及近邻的超参数。

由于传统SBL 算法在实现每次迭代时使用矩阵求逆，对于高维度数据复杂性太高，因此文献[17]研究了基于高斯广义近似消息传递稀疏贝叶斯学习算法，通过使用该算法实现SBL 算法中的期望最大化步骤，显著降低了计算复杂度。近几年，基于SBL 的各种改进算法已经在mMTC 多用户检测中被广泛应用[18-22]。

现有SBL 算法都是基于高斯逆伽马（GIG,Gaussian inverse Gamma）先验模型，没有考虑稀疏信号所对应的支撑集中存在的稀疏性，即稀疏信号中的元素是稀疏的，那么其所对应的支撑集向量也是稀疏的。因此，为了更好地利用这个特性，本文提出了一种伯努利高斯逆伽马（BGIG,Bernoulli Gaussian inverse Gamma）先验模型。该先验模型首先引入了一个服从伯努利分布的二元向量作为支撑集向量，通过SBL 算法进行学习，促进重构解的稀疏性。接着，利用信号在多时隙场景传输中所具备的联合稀疏性，通过共享一个服从伽马分布的超参数来增强该重构性质，从而将该模型推广到了MMV 场景中。最后，在GF-NOMA 系统中多个时隙内多用户检测实验结果表明，本文提出的 BGIG-SBL 算法和BGIG-SBL-MMV 算法检测性能优于现有的GIG-SBL 算法。

1 系统模型

本文考虑了一个GF-NOMA 的mMTC 多用户上行链路系统，共有一个基站和K个用户（K>100），系统模型如图1 所示。

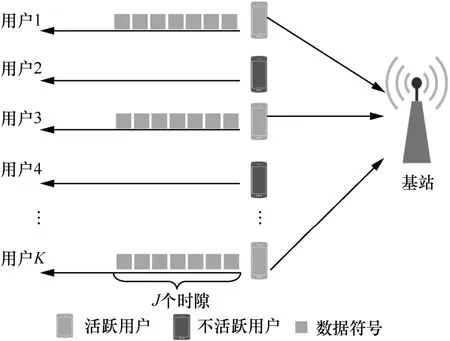
图1 系统模型

每个用户配有一根发送天线且基站配有一根接收天线。系统使用N个子载波来传输信号，其中N＜K。基站在第n个子载波上接收到的信号可以表示为

其中，xk代表第k个用户所发送的符号；φnk代表长度为K的扩频序列φk上的第n个分量；gnk代表用户所在的第n个子载波上的信道增益，是一个具有零均值和单位方差的独立同分布复高斯变量。也就是说，本文考虑的是瑞利衰落信道，该模型广泛应用于无线通信中[23]。vn代表第n个子载波均值为0、方差为η2的加性白高斯噪声。

基站合并N个子载波上的接收信号，接收信号向量可以进一步表示为

H是一个大小为N×K的等效信道矩阵，第n行第k列所对应元素hnk=gnk φnk，h·k代表等效信道矩阵H的第k列，hn·代表H的第n行。如果考虑信号是连续J个时隙发送，则有

其中，yj代表第j个时隙接收到的信号向量；Hj代表第j个时隙的等效信道矩阵，其具体形式是不同时隙内的信道增益gnk(j)乘相同的扩频矩阵φnk；xj代表第j个时隙发送的信号向量；vj代表第j个时隙高斯噪声向量。本文假设用户在发送多个时隙的信号时，活跃用户索引是不变的。这使信号获得了联合稀疏的先验特征，使用此特征将有助于提升稀疏信号的重构性能[24]。

2 GIG-SBL 算法

2.1 分层贝叶斯模型

先回顾一下传统的分层贝叶斯模型，其通过添加GIG 先验模型来重构稀疏解。

在传统的分层贝叶斯模型中，似然函数一般假设服从高斯分布，即是大小为N×N的单位矩阵。

先验函数分为两层，在第一层中，发送信号x通常被假设服从具有零均值的高斯先验分布，即p(x)～ N (0,τ-1)。x的每个分量xk均采用高斯分布建模，即

其中，τ=[τ1,…,τk],=diag(τ)。

第二层中，假设超参数τ服从伽马分布，即p(τ)～Gamma(a,b)。τ是非负超参数，a是形状参数，b是尺度参数。本文把参数a和b设为非常小的值，即 10-4。之所以假设超参数τ服从伽马分布，是因为伽马分布是高斯分布的共轭先验。因此其后验分布和先验分布形式相近，意味着当获得新的数据时能够直接通过参数更新获得新的后验分布，此后验分布将会在下次新数据到来的时候成为新的先验分布。再更新后验分布就不需要通过大量的计算，即

假设噪声参数ε也服从伽马分布，即p(ε)～Gamma(c,d)。设超参数c,d=10-4，有

基于GIG 先验的概率图模型如图2 所示。

图2 基于GIG 先验的概率图模型

2.2 GIG-SBL-SMV 算法

接收端目标是根据单接收信号向量y恢复出稀疏信号x。从图2 可以看出，y分别由2 个变量x,ε控制。超参数τ负责控制稀疏信号x的精度，τ,ε分别取决于超参数a,b和c,d。

在GIG-SBL-SMV 算法中，接收端的后验概率分布p(x,,)在实际中往往无法直接算出。可用变分贝叶斯推断使用另一个模型分布q(x,τ,ε)近似表示。根据平均场理论，该分布可以被完全因式分解为相互独立变量的后验概率分布，即

这里，在更新一个变量的同时，其他变量的最新分布保持固定[18]

对于向量变量z，其估计期望值定义为

此时，稀疏信号x的更新规则为[15]

其中，D:=diag()。可以得到q(x)服从均值为、方差为Φ的高斯分布，即q(x)～ N(,Φ)，更新式如下

另外，精度τ的更新规则为

其中，σ2代表所求协方差矩阵Φ中对应的对角线

进一步地，可以得到τ的更新结果为

最后，噪声参数ε的更新规则为[18]

可以验证出q(ε) 服从伽马分布，即

因此，可以得到ε的更新结果为

传统GIG-SBL-SMV 算法总结如算法1 所示。

算法1GIG-SBL-SMV 算法

3 BGIG-SBL 算法

现有SBL 算法都是基于上述GIG 先验模型进行研究的，忽略了稀疏解中所对应的支撑集中存在的稀疏性。本文提出了一种新的基于伯努利高斯逆伽马的稀疏贝叶斯学习算法，解决稀疏信号重构问题。不同于传统GIG 模型，本文在新先验模型中引入了伯努利先验。该先验参数是一个二元向量，即其元素为0 或1，可通过基于分层贝叶斯模型的SBL算法进行学习。另外，本文利用发送信号所具有的联合稀疏性先验这一特点，通过共享一个控制稀疏度的超参数来提升信号的重构性能。

3.1 BGIG-SBL-SMV 算法

在伯努利高斯逆伽马模型中，稀疏解定义为s◦x，其中，s为二进制支撑集向量，表示稀疏解中非零元素的位置；x为重构稀疏解；◦为哈达玛积，这里表示2 个向量中的对应元素相乘。先验参数s结合了一个参数γ来决定重构稀疏信号所对应的支持集中存在的稀疏性。

本文假设向量s中的各个元素sk服从伯努利分布，即p(sk)～Bernoulli(γk)，以及

向量γ中的各个元素γk假设服从贝塔分布，即p(γk)～Beta(α0,β0)。

其中，α0和β0是支撑集向量γ的初始超参数，文献[25]证明了为向量s的初始超参数分配较大的值会使信号对应的支撑集中具有更多的连续性，因此这里将超参数α0和β0分别设为1.4 和2。这里选择伯努利分布和贝塔分布，是因为两者存在着共轭分布属性。此外，剩下的参数仍与上文提到的GIG 模型一致，服从相同先验分布，即p(x)～N(0,τ-1),p(τ)～Gamma(a,b),p(ε)～Gamma(c,d)。

本文将这种基于单观测向量y的伯努利高斯逆伽马的稀疏贝叶斯学习算法称为BGIG-SBL-SMV。本文提出的基于BGIG 先验的概率图模型如图3 所示。

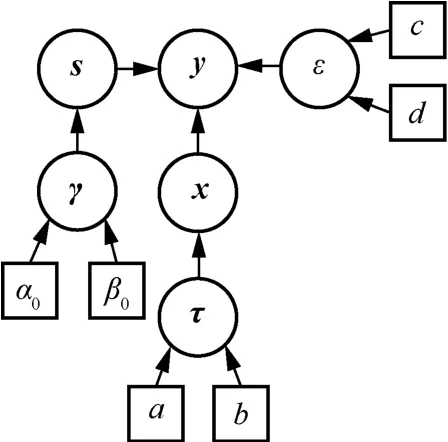
图3 基于BGIG 先验的概率图模型

由于本文在传统GIG 模型中加入了一个支撑集向量s，稀疏解被定义为s◦x。因此，尽管2 个模型中很多参数的先验分布基本是相同的，但是BGIG-SBL-SMV 中参数的更新规则相较于传统的GIG 模型有所区别，各个参数的更新规则如下。具体式推导如附录1 所示。

1) 支撑集向量s的更新规则为

进一步地，可以得到参数s中第k个元素sk的更新规则为

2) 控制支撑集向量s的参数γ更新规则为

从而可以得到参数γ的更新规则为

3）稀疏信号x的更新规则为

其均值和方差分别更新如下

4) 控制稀疏信号x的精度τ更新规则为

则参数τ的更新式为

5) 噪声参数ε的更新规则为

则ε的更新式为

本文提出BGIG-SBL-SMV 算法如算法2 所示。

算法2BGIG-SBL-SMV 算法

3.2 BGIG-SBL-MMV 算法

传统基于MMV的SBL算法将原来单个的观测向量y扩展出J个接收时隙的多个接收信号向量[y1,y2,…,yJ]并行处理，而在此过程中，观测矩阵φ依旧是不变的。通过共享从伽马分布中提取的公共超参数τ，与贝叶斯推理相结合生成了一种新的MSBL 算法[13]。

然而，本文考虑的是实际mMTC 传输场景，即信道状态在多个时隙内是随机变化的。而之前mMTC 传输场景中基于SBL 的多用户检测算法依旧是假设信道增益g和扩频矩阵φ在多个时隙内是不变的，从而也就没有对等效信道矩阵H分时隙来考虑[20]。本文的MMV模型与之前的MMV模型不同之处在于，本文考虑了信道增益g在多时隙发送时是随时间变化的，这更符合实际mMTC 无线通信场景。扩频矩阵φ依旧保持不变，但由于扩频矩阵φ与不同的信道增益gnk(j)相乘，因此等效信道矩阵H划分成了多个时隙[H1,H2,…,HJ]。

本文将提出的BGIG-SBL 算法推广到上述的MMV 模型中，提出了BGIG-SBL-MMV 算法，来进一步提高稀疏信号的重构性能。在该 MMV模型中，BGIG-SBL-MMV 算法仍假设各参数具有与3.1 节相同的先验分布，即

定义对于任意向量zj，有标量zk,j∈zj,∀k=1,2,…,K，zk,j为第j个向量zj中的第k个元素，j=1,2,…,J。基于MMV 的BGIG-SBL 先验概率图模型如图4 所示。

图4 基于MMV 的BGIG-SBL 先验概率图模型

所提BGIG-SBL-MMV 算法各个参数的更新规则如下，具体推导如附录2 所示。

1) 第j个时隙支撑集向量sj的更新规则为

进一步地，可以得到sj中第k个元素sk,j的更新式为

2) 第j个时隙的控制sj的精度参数γj的更新规则为

由此得到参数γj的更新式为

3) 第j个时隙的发送信号xj的更新规则为

其均值和方差更新式分别为

4) 给定J个xj信号控制精度参数τ的更新规则为

从而得到参数τ的更新式为

其中，是协方差矩阵Φj中对应的对角线元素，即=diag(Φj)。可以看到，超参数利用J个不同时隙的信号参数，加强了重构解的联合稀疏性，而且由于与高斯似然共轭，可以方便地进行贝叶斯推理。

5) 第j个时隙噪声参数εj的更新规则为

因此，可以得到参数εj的更新式为

所提BGIG-SBL-MMV 算法如算法3 所示。

算法3所提BGIG-SBL-MMV 算法

4 算法仿真结果及分析

本节在一个GF-NOMA系统中测试所提方案的性能。与文献[7,18]相似，本文设置该多用户mMTC通信中的总用户数K=108，子载波数N=72，活跃用户数M=12，时隙J=7，采用BPSK 调制。这里比较不同算法在多时隙传输场景的检测性能，指标包括误码率（BER,bit error rate）、活跃度差错率（AER,activity error rate）、均方误差（MSE,mean squared error）和归一化均方误差（NMSE,normalized mean squared error）。

定义BER 为重构信号后的错误比特数与总传输比特数的比值，AER 为估计的活跃用户索引出错个数与总活跃用户索引个数的比值。MSE 和NMSE分别定义为[10,12]

采用GIG-SBL-SMV 算法[26]和GIG-SBL-MMV算法作为对比算法，多时隙传输场景下不同SBL 算法在不同信噪比（SNR,signal to noise ratio）下的BER 如图5 所示。从图5 可以看出，在SNR=2～8 dB时，在单测量向量 SMV 方案下，本文提出BGIG-SBL-SMV的性能优于传统GIG-SBL-SMV约1 dB。这是因为所提方案引入一个二元伯努利向量来学习活跃用户索引的信号稀疏性，提高了稀疏信号的重构性能。从图5 还可以看出，在多测量向量MMV 架构下，所提BGIG-SBL-MMV 算法相对于传统GIG-SBL-MMV 算法有2 dB 的性能增益，同时比单测量向量BGIG-SBL-SMV 算法有4 dB 的性能增益。因为前者在处理多个时隙信号时，共享了控制稀疏解的超参数，提高了解的联合稀疏性和重构性能。

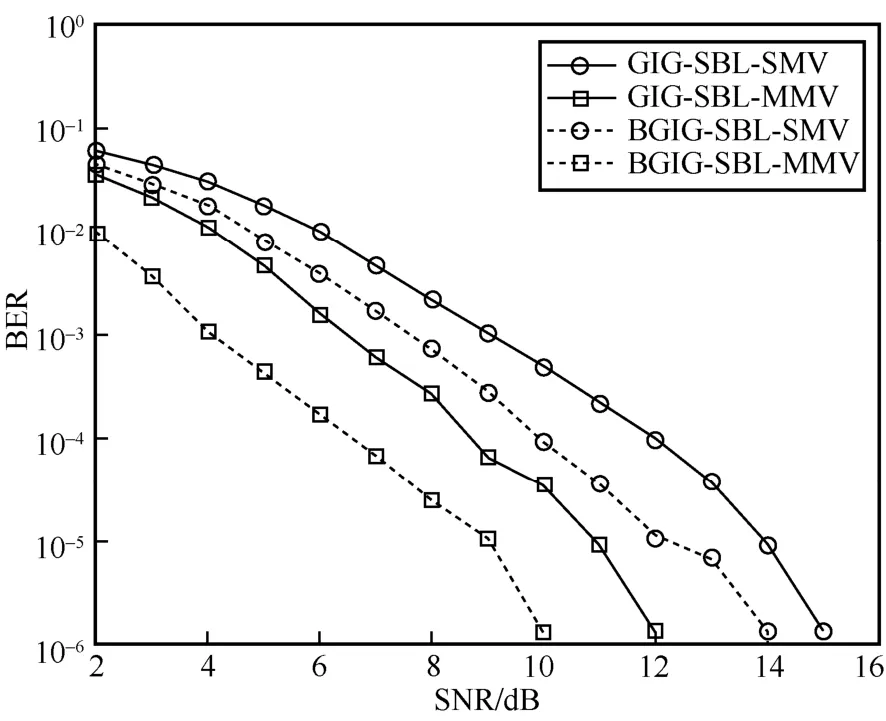
图5 不同SBL 算法的BER

多时隙传输场景下，不同SBL 算法在不同信噪比下的AER 如图6 所示。从图6 可以看出，在相同的AER 时，所提BGIG-SBL-SMV 算法优于传统的 GIG-SBL-SMV 算法约 1 dB，同时与所提BGIG-SBL-MMV 相差约2 dB。

图6 不同SBL 算法的AER

图7 和图8 分别展示了不同信噪比下发送端的原始信号与接收端检测出的信号之间的MSE与NMSE。从图中7 和图8 可以看出，随着SNR的增加，检测出的信号值与原始发送信号值之间的差异会越来越小。所提BGIG-SBL-MMV 相较于其他算法具有显著的性能优势，具体来说，在MSE 或NMSE 相同时，其相较于GIG-SBL-MMV有约2 dB 的性能增益，相比BGIG-SBL-SMV 有约4 dB 的性能增益，相较于GIG-SBL-SMV 有约5 dB 的性能增益。这是因为BGIG-SBL-MMV 不仅通过本文提出的二元伯努利向量来学习活跃用户索引，同时在处理多时隙信号时，共享控制重构稀疏解的超参数，从而保证了估计信号的联合稀疏性。

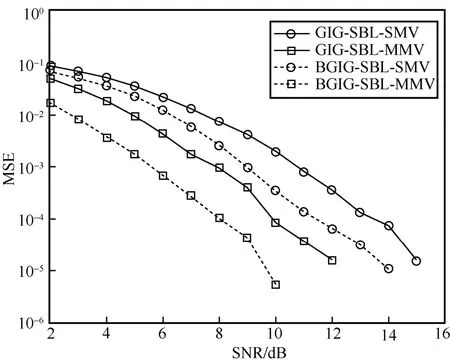
图7 不同SBL 算法的MSE

图8 不同SBL 算法的NMSE

不同SBL 算法在不同活跃用户度Pa下的BER性能如图9 所示。从图9 可以看出，当SNR=6 dB 时，所提BGIG-SBL-SMV 算法在Pa较小时，即Pa<0.2时，具有良好的检测性能。例如，在Pa=0.1 时，BGIG-SBL-SMV 算法相较于传统的GIG-SBL-SMV算法检测性能更好。但是随着活跃用户度的增加，当活跃用户度大于0.2 时，BGIG-SBL-SMV 算法检测性能会逐渐和传统的GIG-SBL-SMV 算法持平。这是因为SBL 算法本身利用了传输信号的稀疏性，因此其只适用于活跃用户少的场景，不适合活跃用户多的场景。而本文提出的BGIG-SBL-MMV 算法在不同活跃用户度下相较于其他算法依旧维持着较高的性能。比如GIG-SBL-MMV算法在Pa=0.1时可达到BER在10-3数量级，而BGIG-SBL-MMV 算法在更多活跃用户下，即Pa=0.15 时，也达到相同的BER 性能。

图9 不同活跃用户度下的仿真结果

5 结束语

本文提出了一种基于伯努利高斯逆伽马先验模型的稀疏贝叶斯学习算法，通过引入一个二元伯努利向量来学习稀疏信号所对应的支撑集中存在的稀疏性。同时将BGIG-SBL 算法扩展到多测量向量MMV 模型中，共享了控制稀疏解的超参数，利用了信号的联合稀疏解特点，进一步提升多用户信号的重构性能。实验结果表明，在mMTC 多用户检测场景中，本文提出的BGIG-SBL-SMV 以及BGIG-SBL-MMV 算法的重构性能显著优于现有的GIG-SBL-SMV 和GIG-SBL-MMV 算法。此外，基于MMV 多测量向量的检测方案BGIG-SBL-MMV相对单测量向量BGIG-SBL-SMV和GIG-SBL-SMV方案，分别有2 dB 和4 dB 的性能增益，同时能检测更多的活跃用户。

附录1 BGIG-SBL 算法各参数更新规则推导过程

1) 支撑集向量s更新规则式(25)推导如下[25,27]

其中，ψ是伽马函数的对数导数，即

由于sk是一个随机的二元伯努利变量，因此

2) 支撑集向量s的参数γ更新规则式(26)推导如下

可以验证q(γ) 服从贝塔分布，即

3) 稀疏重构信号x的更新规则式(28)推导如下

可以验证q(x) 服从高斯分布，即

4) 控制稀疏信号x的精度τ更新规则式(32)推导如下

可以验证q(τ) 服从伽马分布，即

5) 噪声参数ε的更新规则式(34)推导如下

由此可以验证q(ε) 服从伽马分布，即

附录2 BGIG-SBL-MMV 算法各参数更新规则推导过程

1)sj的更新规则式(38)推导如下

其中，hnk,j代表第j个等效信道矩阵Hj中的第n行第k列上的元素，从而有

因为sk,j是一个随机的二元伯努利变量，有

由此可以验证

2)γj的更新规则式(40)推导如下

则可以验证q(γj)～Beta(αj,βj)。

3)xj的更新规则为

由此，如式(41)，可验证

4)τ的更新规则式(45)推导如下

通过推导可得

5)εj的更新规则式(47)推导如下

由此，可以验证