一道椭圆探索性问题的再推广

北京市第十二中学(100071)蒋海燕 刘刚

文[1]给出了下面的问题及推广:

引例已知椭圆经过点A1(-2,0),A2(2,0),点B为椭圆E的上顶点,且直线A1B与直线相互垂直.

(1)求椭圆E的方程;

(2)若不垂直于x轴的直线l过椭圆E的右焦点F2,交椭圆E于C,D两点(C在x轴上方),直线A1C,A2D分别与y轴相交于S,T两点,试判断是否为定值?(答案 (1);(2)是定值,且定值为.)

在此基础上,得到了下面的推广:

借助几何画板软件探究,发现点P可以是x轴上除椭圆左、右顶点外的任一定点,y轴变为定直线x=n,依然有相应的定值性质,于是再推广,得到:

性质1如图1,已知椭圆的左、右顶点分别为A1,A2,过点P(m,0)(m±a) 作斜率不为0 的直线与椭圆E交于C,D两点, 直线l:x=n(n±a)与x轴交于点Q,直线A1C,A2D与l分别交于S,T两点,则.

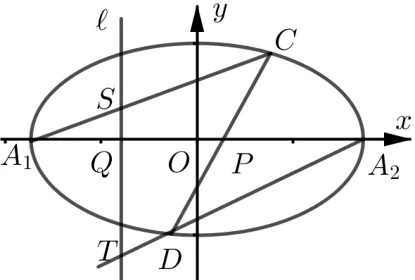
图1

证明设C(x1,y1),D(x2,y2), 直线CD的方程为x=ty+m, 与椭圆E的方程联立, 得(b2t2+a2)y2+2tmb2y+b2m2-a2b2=0,则

由已知得A1(-a,0),A2(a,0), 所以直线A1C的方程为, 令x=n, 得.又直线A2D的方程为, 令x=n, 得,注意到: 由①得,所以

故结论得证.

由椭圆类比双曲线、抛物线,有:

性质2已知双曲线的左、右顶点分别为A1,A2,过点P(m,0)(m±a)作斜率不为0 的直线与双曲线E交于C,D两点, 直线l:x=n(n±a)与x轴交于点Q,直线A1C,A2D与l分别交于S,T两点,则.(证明从略,读者可参考性质1 的证明过程自行完成.)

性质3如图2, 已知抛物线E:y2= 2px(p> 0) 的顶点为O, 过点P(m,0)(m0)的直线与抛物线E交于C,D两点, 直线l:x=n(n0)与x轴交于点Q,直线OC与l交于点S,过D作l的垂线,垂足为T,则.

图2

证明设C(x1,y1),D(x2,y2), 直线CD的方程为x=ty+m, 与抛物线E的方程y2= 2px联立, 得y2-2pty-2pm=0,则

又直线OC的方程为,令x=n,得.又yT=y2,注意到: 由②可得ty1y2=-m(y1+y2),于是

故结论得证.