高考数学试卷中问题情境的比较研究

王智宇，张维忠

高考数学试卷中问题情境的比较研究

王智宇1，2，张维忠1

（1．浙江师范大学 教育学院，浙江 金华 321004；2．浙江台州市路桥中学，浙江 台州 318000）

人工智能时代，教育教学的最终目的是发展学生的核心素养．能否科学地评价问题情境已经成为落实素养导向的教与学的关键．研究尝试从“复杂性水平”和“任务难度水平”2个维度以及“背景化水平”“知识与技能水平”“表征水平”“运算水平”和“认知水平”5个因素构建高考数学试卷中问题情境的评价框架，并选取2020—2022年的新高考I卷、2022年的浙江高考卷和2022年的上海高考卷共5套试卷进行比较与分析，由此得到关于高考数学试卷中问题情境设计的若干启示：植根于真实性，提高背景化水平；基于综合性，强化知识与技能的整合；立足于多样性，拓展混合表征的内容载体；体现开放性，培养数学创造性思维．

高考数学试卷；问题情境；评价框架；比较研究

1 问题提出

20世纪80年代末，情境认知和学习理论兴起，心理学和人类学视角下的知识观和学习观发生了重大转变，即强调知识具有情境性，不是客观确定的，也不是主观创造的，而是学习者在特定的情境脉络中不断地理解和建构中产生的．情境是一切认知活动的基础[1]．人工智能时代，教育教学的最终目的是发展学生的核心素养，而核心素养的培养需要将学生置身于真实的问题情境中，亲历复杂问题的解决过程．情境及情境中问题的复杂程度构成了数学核心素养水平划分的基础[2]，问题情境蕴含了情境的问题化和问题的情境化，是数学内容、情境内容和学生经验内容的融合[3]．因此，如何科学地评价数学问题情境已经成为落实素养导向的教与学的关键问题，并日益受到关注．陈志辉从“数学特征水平”“数学表征水平”“任务特征水平”和“情境类型”4方面对中考数学试题进行了比较[4]．李健等构建了初中数学教科书问题情境质量评价的“金字塔”模型[5]．邓海英等将“数学问题情境解决”划分为“知识理解”“知识迁移”和“知识创新”3种水平[6]．李保臻等从“内容编排与分布”“类型及数量”“真实性水平”“表征特征”4个方面对教科书中的数学建模问题情境进行了比较分析[7]．

然而，目前缺乏专门针对高考数学试卷中问题情境的评价研究．国务院自2014年颁布《关于深化考试招生制度改革的实施意见》以来，有14个省份已经实施新高考，另有15个省份已经启动新高考．2019年教育部发布《中国高考评价体系》，明确提出将情境作为高考评价体系的考察载体，对情境进行分类，对情境活动进行分层，发挥情境在考查学生“必备知识”“关键能力”“学科素养”和“核心价值”4个层面的表现水平[8]．因此，开展高考试卷中问题情境的评价研究显得尤为迫切．研究者构建了高考数学试卷中问题情境的评价框架，以期为高考数学试卷的设计与评价提供一点参考．

2 研究设计

2.1 研究对象

上海市和浙江省是高考综合改革试点地区．自2023年起，浙江省高考数学科目使用教育部考试中心命制的全国新高考I卷．因此，对浙江卷、上海卷和全国新高考I卷的比较与分析具有鲜明的时代意义．研究选取了2020年至2022年的3套新高考I卷（以下分别简称为20年I卷，21年I卷，22年I卷）和2022年浙江卷（以下简称浙江卷）、2022年上海卷（以下简称上海卷）合计5套试卷作为研究对象．

2.2 分析框架

2.2.1 分析因素的确定

比利时教育学家罗日叶在20世纪90年代提出整合教学法，并在许多欧洲和非洲国家推行教学改革，产生了重要影响．整合教学法的核心理念是学校教育应该把发展学生在真实社会情境的能力作为最终目标，其关键途径是设计靶向情境，评估学生的学业获得．这里的靶向情境是认知心理学中的“实施情境”的一个子集，指的是教师为了评估学生对于学业的整合能力而设计的问题情境，与中国高考试卷中的问题情境具有相同的功能指向．罗日叶将问题情境理解为“针对某个既定的任务，要求学生联结起来的一组背景化的信息”．一个复杂的问题情境包含“复杂性水平”和“任务的复杂化”两大特征．其中，情境的“复杂性水平”主要取决于3个因素：一是情境的背景化，指的是学生和背景之间的亲近程度，与学生已有的学习经验、学习兴趣和学习环境等因素有关；二是需要调动的基本知识和技能的性质和数量；三是联结这些知识和技能的方式，在数学学科中包括具有一定功能性的图形的联结、各个已知条件之间的联结、规则和公式之间的联结等．“任务的复杂化”主要取决于学生完成学习任务所使用方法的认知水平、情感水平或动作水平．需要说明的是，“任务的复杂化”的变化取决于“复杂性水平”变化后是否增减了新的限制条件、方法和程序[9]．数学问题情境是以数学内容为载体，具有一定的复杂性水平并指向一定任务难度水平的环境，并确定了复杂性水平维度（包含“背景化水平”“知识与技能水平”和“表征水平”3个因素）和任务难度水平维度（包含“运算水平”和“认知水平”2个因素）作为高考数学试卷中问题情境的评价框架的内容．

2.2.2 分析框架的确定

为便于统计和分析，对评价框架中的2个维度和5个因素进一步地细化，如表1．“背景化水平”指向学生对于数学问题产生的背景的熟悉和亲近程度，体现为学生对数学与现实世界以及数学内部关联性的感知程度．《普通高中数学课程标准（2017年版）》（以下简称课标）将问题情境划分为“现实情境”“数学情境”“科学情境”3种类型，每个类型划分为“熟悉的”“关联的”“综合的”3个层次[10]．2021PISA数学素养测试框架根据问题情境与学生生活的距离，由近到远将情境划分为“个人情境”“职业情境”“社会情境”和“科学情境”4种类型[11]．从高考试题的情境类型和内容来看，课标的划分比较笼统，对3个层次的边界也没有明确说明．PISA测试框架将“数学情境”归结为“科学情境”存在两个缺陷：一是高考数学试题以数学知识为载体，都属于“科学情境”；二是学生对“考查单一主题模块的知识”与“考查多个主题模块的知识”的试题的熟悉程度是不一致的．综合上述观点，问题情境的背景化水平划分为“熟悉的数学情境”“现实生活情境”“社会文化情境”“关联的数学情境与科学情境”4个水平层次．

“知识与技能水平”指向学生理解问题情境必须调动的知识与技能的数量．一般来说，一个问题情境如果需要调用更多知识与技能，那么它更具有复杂性．知识与技能水平可以划分为“1个知识与技能”“2个知识与技能”“3个知识与技能”和“4个及以上知识与技能”4个层次．

“表征水平”指向学生联结不同的数学知识与技能所利用的表征方式．徐斌艳等人将数学表征能力界定为“用某种形式，例如书面符号、图形（表）、情境、操作性模型、文字（包括口头文字）等，表达要学习的或处理的数学概念或关系，以便最终解决问题”[12]．表征水平可以划分为“单一型表征”“组合型表征”“复合型表征”和“混合型表征”4个水平层次．

“运算水平”指向学生完成问题情境中的任务内容所具备的运算能力．朱立明认为数学运算能力是指在理解运算对象的基础上，确定运算的方向，并根据法则、公式、定理，合理计算或估计运算结果的能力[13]．结合课标中关于数学运算素养水平的划分方法[10]，运算水平可以划分为“简单运算”“综合运算”“较复杂运算”和“复杂运算”4个层次．

“认知水平”指向学生完成问题情境中的任务内容所经历的认知过程．修订后的布鲁姆认知分类理论将认知过程从简单到复杂划分为“记忆”“理解”“应用”“分析”“评价”“创造”6个层次，并细分为19个具体的认知过程[14]．认知水平可以划分为“理解”“应用”“分析”和“创造”4个层次．

表1 高考数学试卷中问题情境的评价框架

为了保证统计结果的科学性，成立了一个编码小组，包括1名数学教育博士生和2名多次参与命制省市联考试题的高中数学教师．小组成员首先利用评价框架对高考卷中的部分试题进行独立编码，然后论证评价框架的科学性并进行调整，再对所有试题进行编码，最后对存在异议的编码进行讨论并形成统一认识．

下面举例说明如何应用评价框架对高考试卷中的问题情境进行统计分析．

表2 量化结果

3 研究结果的比较与分析

3.1 复杂性水平维度的比较与分析

首先，由图1可知，5套试卷的“复杂性水平”从高到低依次是20年I卷、22年I卷、浙江卷、21年I卷和上海卷．其中，3套新高考I卷“复杂性水平”存在明显波动，按时间先后顺序呈现先下降后上升的趋势，平均水平为6.31，高于浙江卷和上海卷的水平值．21年I卷和上海卷水平非常接近．

图1 5套试卷的复杂性水平比较

表3 5套高考试卷中109道试题的问题情境量化统计

3.1.1 背景化水平的比较与分析

由图2知，5套试卷的“背景化水平”从高到低依次是20年I卷、22年I卷、21年I卷、上海卷和浙江卷．20年I卷中有8道题属于“非熟悉的数学情境”，超过该套试卷总题数的1/3．3套新高考I卷的平均水平是1.47，明显高于浙江省和上海卷．由图3知，5套试卷中属于“熟悉的数学情境”“现实生活情境”“社会与文化情境”和“关联的数学情境与科学情境”的题数分别占比82.6%、5.5%、6.4%、5.5%，表明情境类型以“熟悉的数学情境”为主．对19道不属于“熟悉的数学情境”的试题所考查的内容作进一步梳理，可以发现考查“概率统计”主题知识的题数有9道，考查“三角函数、立体几何以及解析几何”主题知识之间的关联的题数有4道，这两类试题数量合计占比接近70%，表明5套试卷更加侧重于考查概率统计主题模块知识与现实世界的关联以及数学内部不同主题模块知识的关联．

图2 5套试卷的背景化水平比较

图3 各个层次的情境试题所占比重

3.1.2 知识与技能水平的比较与分析

由图4可知，5套试卷的“知识与技能水平”从高到低分别是22年I卷、浙江卷、20年I卷、21年I卷和上海卷．其中，20年I卷与22年I卷以及浙江卷水平较为接近，21年I卷和上海卷较为接近．5套试卷的题型结构存在较大不同，新高考I卷由8道单选题、4道多选题、4道填空题、6道解答题组成，浙江卷由10道单选题、7道填空题、5道解答题组成，上海卷由12道填空题、4道单选题、5道解答题组成．对不同题型的水平均值进行计算，由图5可知，3套新高考I卷中多选题的水平均明显高于单选题．以22年I卷多选题第10题为例，该题选项中涵盖了“利用导数运算求极值点，判断零点个数，求切线方程以及研究函数的对称性”等知识与技能．22年I卷，浙江卷和上海卷解答题的水平均值在3.5左右，明显高于其它题型．20年I卷的填空题以及浙江卷的单选题的水平明显高于其它试题，表明5套试卷中不同题型中的知识与技能数量的分布存在差异．

研究进一步统计了知识与技能的类型和数量，为了便于统计，按课标的内容说明对知识进行归类，比如将“理解三角函数图象的平移变换、求三角函数的最值、三角函数的单调性等”归为“三角函数的概念和性质”．由如图6可知，5套试卷总共涵盖了37类知识与技能，重点考查了“基本立体图形及其位置关系、函数的性质、导数的几何意义及在研究函数中的应用、三角函数、圆锥曲线的定义与性质、直线与圆锥曲线的位置关系以及平面向量的运算与空间向量的应用”等内容，较少考查“统计与概率”主题模块知识，尚未考查“数学建模活动与数学探究活动”主题模块知识．

图4 5套试卷的知识与技能水平比较

图5 各题型的知识与技能水平比较

图6 5套高考试卷所涵盖的知识与技能的类型与数量

3.1.3 表征水平的比较与分析

由图7可知，5套试卷中，21年I卷的表征水平最低，其余4套试卷没有明显差距．由图8可知，5套试卷中属于“组合型表征”水平的题数最多，其次是属于“复合型表征”的题数，“单一型表征”和“混合型表征”的题数非常少，表明5套数学试卷主要考查学生理解和运用数学符号表达数学问题的能力．其中，“组合型表征”主要体现在表征“函数图象与性质、导数的几何意义、直线与圆的位置关系、直线与圆锥曲线的位置关系、立体图形的体积及空间角、分类变量的统计数据和随机变量的分布列”等内容．“混合型表征”体现在表征“球与正四棱锥、球与直四棱柱以及双曲线与三角形的位置关系”等内容．此外，5套试卷中“复合型表征”和“混合型表征”的题数合计占比超过1/3，其中20年I卷和22年I卷以及浙江卷占比都超过40%，表明这3套高考试卷对学生“利用图形和表格表征数学概念及其关系的能力”有更高的要求．以22年I卷第21题为例，学生需要先表征出双曲线内接一个三角形的图形，然后表征出直线的倾斜角，直线与渐近线的位置关系，直线与双曲线的位置关系以及直线与直线的对称关系，最后逐步求直线的斜率，直线与双曲线的交点坐标，内接三角形的边长和面积．

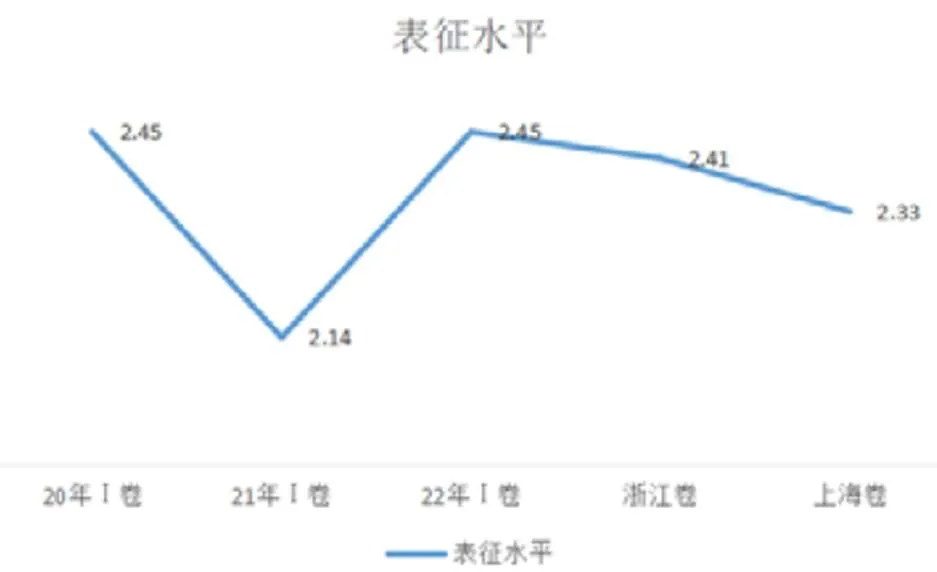
图7 5套试卷的表征水平比较

图8 各个层次的题数比较

3.2 任务难度水平维度的比较与分析

由图9可知，5套试卷的“任务难度水平”从高到低依次是22年I卷、浙江卷、20年I卷、上海卷和21年I卷，后3套试卷的水平比较接近．22年I卷的水平相比20年I卷和21年I卷有明显提升．2020年教育部考试中心首次命制新高考I卷，仅有山东一省选取该套试题，2021年广东、湖南、湖北、河北、福建5省以及2022年江苏省选用该套试题，或许更多地区选用新高考I卷成为“任务难度水平”波动的一个因素．

图9 5套试卷的任务难度水平比较

3.2.1 运算水平的比较与分析

由图10可知，5套试卷中运算水平最高的是22年I卷，其次是浙江卷．20年I卷与上海卷水平非常接近，21年I卷水平最低．由图11可知，5套试卷中属于“简单运算”“综合运算”“较复杂运算”和“复杂运算”的试题比例分别为33.0%、40.4%、23.9%、2.8%，表明5套试卷主要考查学生明确和转化运算问题，合理选择运算方法，设计运算程序从而解决问题的能力，而对“复杂运算水平”的考查限定在较小范围内．3套新高考I卷中，20年I卷和21年I卷运算水平接近且较低，2套试卷试题在“复杂运算”水平层次没有体现．22年I卷中达到“较复杂运算水平”和“复杂运算”水平的题数是另外2套试卷的2倍，表明新高考I卷逐渐重视考查学生转化运算问题的能力．上海卷中属于“简单运算”和“较复杂运算”的题目最多，属于“综合运算”的题数最少，表明运算水平整体梯度较大，尽管与20年I卷相比整体水平均值差不多，但对学生运算能力的考查要求更高．浙江卷更加重视考查学生进行“复杂运算”的能力．以该卷第22题第2问的2个小题为例，第1小题的运算程序是先设切线方程，再将方程的根转化为函数的零点，然后根据零点的个数对函数进行求导，最后利用导数研究函数的性质证明不等式．第2小题的运算程序是先对函数的单调性进行分类讨论，然后对不等式进行放缩，再通过换元法构造一元二次方程，最后证明不等式．这表明“复杂运算”的基本特征是“创造性”，表现为“多个运算问题的转化，多个运算步骤的设计以及多种运算技能和方法的运用”．

图11 运算水平各层次题数比重

3.2.2 认知水平的比较与分析

由图12可知，5套试卷中“认知水平”最高的是22年I卷，其次是浙江卷，其余3套试卷水平比较接近．根据布鲁姆的认知水平分类方法，“理解”与“应用”属于“低认知水平”，“分析”和“创造”属于“高认知水平”．经过统计，由图13可知，属于“低认知水平”和“高认知水平”的题数分别占比59.6%和40.4%．20年I卷属于“低认知水平”题数占比最高达68.2%，达到“应用”水平的题数是“理解”水平的4倍，表明其侧重考查学生应用知识的能力．22年I卷达到“高认知水平”的题数占比最高为50%，表明其更重视考查学生分析知识的关联性的和创造性的运用知识的能力．22年I卷、浙江卷和上海卷均有达到“创造”水平的试题，以上海卷的第21题为例，该题由3个小题构成，涉及“逻辑用语、数列的递推公式、数列的单调性、等差数列的通项公式”4个内容和“数学归纳法、反证法、构造法、分类讨论”4种方法．其中，第3小问的解题程序是先构造递推公式并利用第2问的结论将问题转化为3个含参数的等式关系，然后利用数学归纳法证明数列的单调性，最后对参数进行分类讨论，对数列中的项的个数分奇偶讨论并利用反证法确定数列的通项公式．该题较好地体现了获得“创造”的3个阶段：第一阶段是将新出现的学习任务准确地表征为数学问题；第二阶段是分析数学问题演变的各种可能性从而形成解决方案，第三阶段是能够利用数学知识技能和思想方法执行解决方案．

图12 5套试卷的认知水平比较

图13 高低认知水平的题数比例

4 研究结论与启示

以数学核心素养为导向的评价应当凸显学生面对真实复杂情境的问题解决能力．将“复杂性水平”和“任务难度水平”作为评价高考试卷中问题情境的两个重要维度，并基于上述比较与分析的结果，得到如下一些结论与启示．

4.1 植根于真实性以提升背景化水平

素养的核心是真实性，真实性的根本属性是“情境性”．5套高考数学试卷中属于“熟悉的数学情境”的题数占比过高，导致背景化水平较低．研究表明：这类数学问题不能够激发学生的学习动机，无法让学生完整地经历问题解决以及建立关于理解的记忆，学生容易习得惰性知识，而惰性知识无法被应用于真实的问题解决，阻碍了素养的形成[17]．杜威也认为“要为学生创设一个真实的经验的情境，并且在这个情境内部产生一个真实的问题，作为思维的刺激物”[18]．

因此，高考命题应注重将数学问题植根于真实性的情境，从数学内部的发展脉络、现实生活、社会热点、历史文化以及科技成果的应用等方面寻找数学问题的原型并进行逆向设计．同时，命题要整体把握学生对于情境的熟悉程度．如果情境对学生而言太过陌生，脱离了学生已有的学习经验，那么它可能给学生带来较大的思维障碍．如果情境对学生而言过于熟悉，那么它的教学和评价功能会得到削弱．除此之外，命题还应当充分考虑属于不同层次的情境的比例问题．

4.2 基于综合性以优化知识与技能的整合

知识是数学核心素养产生的本源，对核心素养的评价应着重于对由知识学习转化而来的能力的评价[19]．问题情境的一个重要功能是评估学生整合知识与技能的能力．5套试卷中所考查的知识与技能主要来自于“函数”“几何与代数”两大主题模块，较少来自“概率与统计”主题模块的，几乎没有涉及“数学建模活动与数学探究活动”主题模块，表现出一定的倾向性，容易形成“高考试题考查的内容不够全面”的误解．“概率与统计”“数学建模活动与数学探究活动”两大主题模块蕴含着丰富的数学内容和思想方法．“概率与统计”的研究对象是随机现象，为人们从不确定性的角度认识客观世界提供重要的思维模式和解决问题的方法．“数学建模活动”是人们基于数学思维运用数学模型解决实际问题的一类综合实践活动．它们都是高中数学课程中不可分割的内容，是培养学生数据分析和数学建模素养的重要载体[20]．此外，各套试卷中都有一定比例的试题涉及4个及以上知识与技能．从题型上看，多选题和解答题考查的知识与技能个数平均超过3个，具备较强的综合应用性．

因此，高考命题要更加重视数学知识与技能的全面性，加强考查学生在真实的问题情境中运用概率和统计的思维收集、处理和分析数据的能力以及发现、提出，分析、构建数学模型来解决数学问题的能力[21]．同时，高考命题要保持“知识与技能”的总体水平，优化不同题型的水平梯度，重视知识间的关联，体现知识的综合性，引导学生构建完整的、系统的知识体系，进一步加强迁移和整合知识的能力．

4.3 立足多样性拓展以混合表征的内容载体

历次PISA测试都将“数学表征”作为评价数学素养的重要因素，数学核心素养中关于“数学抽象”“直观想象”和“数学建模”等的描述与“数学表征”密切相关．此外，有研究表明学生使用多元表征比单个表征更有助于理解数学知识及其关联[22]．5套高考试卷中的问题情境的表征形式总体呈现多样性，但属于“组合型表征”和“复合型表征”的题数占比过高，“混合型表征”的题数占比过低，并且“混合型表征”的内容和形式以“通过作图描述平面和空间中几何元素的位置关系”，较为单一．此外，试卷中尚未出现“用多种表格或图与表混合表征”的试题．

因此，高考命题要拓展混合表征的数学对象．比如，2019年出版的人教A版高中数学教科书在刻画“函数的关系、各类函数的性质、函数模型的应用、建立数学模型解决实际问题、随机变量的分布、样本数据的统计分析、裴波那契数列、杨辉三角、割线的斜率变化”等内容时使用了多样化的图表进行表征．这些内容可以成为重要的素材来源[23]．

4.4 体现开放性以培养数学创造性思维

当下，培养数学创造性思维无疑成为了发展数学核心素养的引领性任务[24]．创造性思维是一种非逻辑思维，创造性思维的培养有两个关键点：一是鼓励学生在知识材料不充分的基础上进行大胆地猜想和推测；二是为学生提供自由想象的空间，使学生产生丰富的感性体验，建立情感与认知、经验与知识的联系[24]．创造性思维的功能不仅是解决问题，更在于发现、设想、深入地思考问题[25]．通过上述比较和分析，可以发现“运算水平”因素的“复杂运算”层次以及“认知水平”因素的“创造”层次都指向学生运用数学创造性思维分析和解决问题的能力．22年I卷，浙江卷和上海卷中均有所涉及．但这类题目的问题情境由于缺乏真实性、多元性和开放性，涉及的运算问题隐晦，运算程序复杂，认知水平要求高，问题解决的路径长、窄且单一，最终导致“专家解决方案”与“学生解决方案”存在较大差距．

因此，高考命题应当基于学生实际的运算水平和认知水平，创设条件不够充分的、结构不良的、问题解决多元化的、具有创造性空间的开放式真实问题情境，让学生产生积极的情感体验和探究欲望，产生有意义的联想和猜测，将数学问题转化为运算问题，设计运算程序，应用不同的运算方法制定问题解决的方案．

[1] BROWN J S, COLLINS A, DUGUID P. Situated cognition and the culture of learning [J]. Educational Researcher, 1989, 18 (1): 32-42.

[2] 常磊，鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（2）：24-28．

[3] 吴晓红．数学素养——从理论到实践[M]．上海：华东师范大学出版社，2019：108-109．

[4] 陈志辉，刘琼琼，李颖慧，等．PISA影射下数学学业水平考试的问题情境比较研究——以上海三年中考和新加坡O-Level试题为例[J]．比较教育研究，2015，37（10）：98-105，112．

[5] 李健，李海东，宋莉莉．数学教科书问题情境质量评价的“金字塔”模型——基于初中数学教师的教科书使用调查[J]．数学通报，2020，59（12）：20-25，44．

[6] 邓海英，严卿，魏亚楠．数学情境问题解决错误分析与评价[J]．数学教育学报，2021，30（1）：61-67．

[7] 李保臻，陈国益．高中数学教科书中数学建模问题情境的比较研究[J]．数学教育学报，2022，31（3）：6-14．

[8] 教育部考试中心．中国高考评价体系[M]．北京：人民教育出版社，2019：7，18-32．

[9] 罗日叶．为了整合学业获得——情景的设计和开发[M]．汪淩，译．上海：华东师范大学出版社，2010：7，98，106-118．

[10] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：81．

[11] 于国文，陈鹏举，冯启磊，等．PISA数学测评内容和情境演变及其启示[J]．数学教育学报，2019，28（4）：17-23．

[12] 徐斌艳．数学学科核心能力研究[J]．全球教育展望，2013，42（6）：67-74，95．

[13] 朱立明．高中生数学关键能力：价值、特质与操作性定义[J]．天津师范大学学报（基础教育版），2021，22（2）：49-54．

[14] 盛群力，褚献华．布卢姆认知目标分类修订的二维框架[J]．课程·教材·教法，2004，24（9）：90-96．

[15] 鲍建生．中英两国初中数学期望课程综合难度的比较[J]．全球教育展望，2002，31（9）：48-52．

[16] 张维忠，王智宇，胡益芳．中小学数学教材难度研究20年：成果、反思与展望[J]．浙江师范大学学报（自然科学版），2022，45（4）：474-480．

[17] 刘徽．真实性问题情境的设计研究[J]．全球教育展望，2021，50（11）：26-44．

[18] 杜威．我们如何思维[M]．马明辉，译．北京：新华出版社，2010：94-95．

[19] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23，59．

[20] 汪飞飞，张维忠．中国中学数学建模研究的历程与论题及其启示[J]．数学教育学报，2022，31（2）：63-68．

[21] 唐恒钧，周雯馨．澳大利亚“高考”数学文化试题特征及其评析——以2017—2021年VCE进阶数学试题为例[J]．数学教育学报，2022，31（6）：70-74．

[22] 沈阳，张晋宇，鲍建生．表征在数学教育中的研究现状[J]．数学教育学报，2022，31（2）：82-89．

[23] 梁玮，徐斌艳，于文字．近二十年国内数学高考研究进展与启示——基于CiteSpace的可视化分析[J]．数学教育学报，2023，32（2）：18-23，36．

[24] 丁福军，张维忠．创造性思维在数学教材中的呈现研究[J]．浙江师范大学学报（自然科学版），2021，44（2）：234-240．

[25] 张敬威，于伟．非逻辑思维与学生创造性思维的培养[J]．教育研究，2018，39（10）：40-48．

A Comparative Study of the Problem Situation in the Mathematics Test Paper of the College Entrance Examination

WANG Zhi-yu1, 2, ZHANG Wei-zhong2

(1. College of Education, Zhejiang Normal University, Zhejiang Jinhua 321004, China;2. Taizhou Luqiao Middle School, Zhejiang Taizhou 318000, China)

In the era of artificial intelligence, the ultimate goal of education and teaching is to develop students’ core competencies, Whether the problem situation can be scientifically evaluated has become the key to the implementation of competency-oriented teaching and learning. This study attempts to construct a problem situation evaluation framework for the NMET math test paper from the two dimensions of “complexity level” and “task difficulty level”, as well as the five factors of “background level”, “knowledge and skill level”, “representation level”, “operation level” and “cognitive level”. Five sets of test papers are selected for comparison and analysis, including the new NMET I from 2020 to 2022, the Zhejiang NMET in 2022 and the Shanghai NMET in 2022. From this, we can get some enlightenment for the design of problem situations in the of college entrance examination papers: rooted in authenticity, improve the background level; Strengthen the integration of knowledge and skills based on comprehensiveness; based on diversity, expand the content carrier of mixed representation; and embodying openness and cultivating mathematical innovative thinking.

college entrance examination mathematics paper; problem situation; evaluation framework; comparative study

G632.479

A

1004–9894（2023）06–0038–07

王智宇，张维忠．高考数学试卷中问题情境的比较研究[J]．数学教育学报，2023，32（6）：38-44．

2023–06–16

全国教育科学“十三五”规划教育部重点课题——指向深度理解的问题链教学研究（DHA200318）

王智宇（1992—），男，浙江台州人，博士生，主要从事数学课程与教学论研究．张维忠为本文通讯作者．

[责任编校：陈汉君、张楠]