Subordination and Superordination Results for a Certain of Integral Operator Involving Generalized Mittag-Leffler Functions

-,-

(1. School of Engineering and Management, Pingxiang University, Pingxiang 337055, China; 2. School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract: In the paper, by making use of the principle of subordination between analytic functions with the multiplier transforms defined by generalized Mittag-Leffler function,the authors investigate subclasses of univalent analytic functions, such as starlike functions,convex functions, close-to-convex functions and quasiconvex functions.Several inclusion relationships, inequality properties, subordination and superordination results associated with the multiplier transforms are proved and the sandwich-type results are also obtained.Keywords: Analytic functions; Mittag-Leffler function; Differential subordination and differential superordination; Hadamard product (or Convolution)

§1.Introduction

LetAdenote the class of all functions of the form

which are analytic in the open unit disk U={z ∈C:|z|<1}.

Denote bySthe subclass ofAconsisting of all univalent functionsfin U.LetH(U) be the linear space of all analytic functions in U.Forn∈N={1,2,...}anda∈C, we let

LetPdenote the class of functions of the form

which are analytic and convex in U and satisfy the conditionℜ(p(z))>0(z ∈U).

Letf,g ∈A, wherefis given by (1.1) andgis defined by

Then the functionsfandgwith the Hadamard product (or convolution)f ∗gcan be defined by

For two functionsfandg, analytic in U, we say that the functionfis subordinate togin U, and writef(z)≺g(z)(z ∈U), if there exists a Schwarz functionω, which is analytic in U withω(0)=0 and|ω(z)|<1(z ∈U) such thatf(z)=g(ω(z))(z ∈U).As is known to all that

where Γ(·) denotes the Gamma function.

The following three-parametric Mittag-Leffler function (or Prabhakar function) was introduced by Prabhakar [9]

is the well-known Pochhammer symbol.

Mittag-Leffler functions are related to huge application potential and its application may involve application problem, neural network, probability theory, statistical distribution theory.One can see recent works [2,3,13–15].

We consider the following modified Mittag-Leffler function which belong to the classA

Inspired by [10,16,18], in this paper, we aim at proving some inclusion relationships,inequality properties, subordination and superordination properties, and sandwich-type results involving the integral operator of generalized Mittag-Leラer(z).

§2.Preliminaries results

This section is devoted to the definitions and lemmas required to prove our main results.

Denote byQthe set of all functionsfthat are analytic and injective on ¯U-E(f), where

and such thatf′(ε)/=0 forε∈∂U-E(f).

Lemma 2.1.( [1, p.332])Let κ,ϑ∈C.Suppose also thatmis convex and univalent inUwith

If q is analytic inUand q(0)=h(0),then the subordination q(z)+ζ(z)zq′(z)≺h(z)(z ∈U)implies that q(z)≺h(z)(z ∈U).

Lemma 2.3.( [12])Let q be convex univalent inUand ψ,γ ∈Cwith

If p is analytic inUand ξp(z)+λzp′(z)≺ξq(z)+λzq′(z),then p≺q,and q is the best dominant.

Lemma 2.4.( [6, p.132], [5, p.190])Let q ∈Ube univalent and θ,ϕ be analytic in a domainDcontaining q(U)with ϕ(ω)/=0when ω ∈q(U).Set Q(z)=zq′(z)ϕ(q(z)),and h(z)=θ(q(z))+Q(z).Suppose that:

If p∈H[q(0),1]for some n∈Nwith p(U)⊂Dand

then p≺q and q is the best dominant.

Lemma 2.5.( [7])Let q be convex univalent inUand ζ ∈C.Further assume that ℜ(ζ)>0.If p∈H[q(0),1]∩Q and p(z)+ζzp′(z)is univalent inU,then q(z)+ζzq′(z)≺p(z)+ζzp′(z),which implies that q ≺p and q is the best subordinant.

Lemma 2.6.( [8, p.332])Let q be univalent inUand θ,ϕ be analytic in a domainDcontaining q(U).Suppose that:

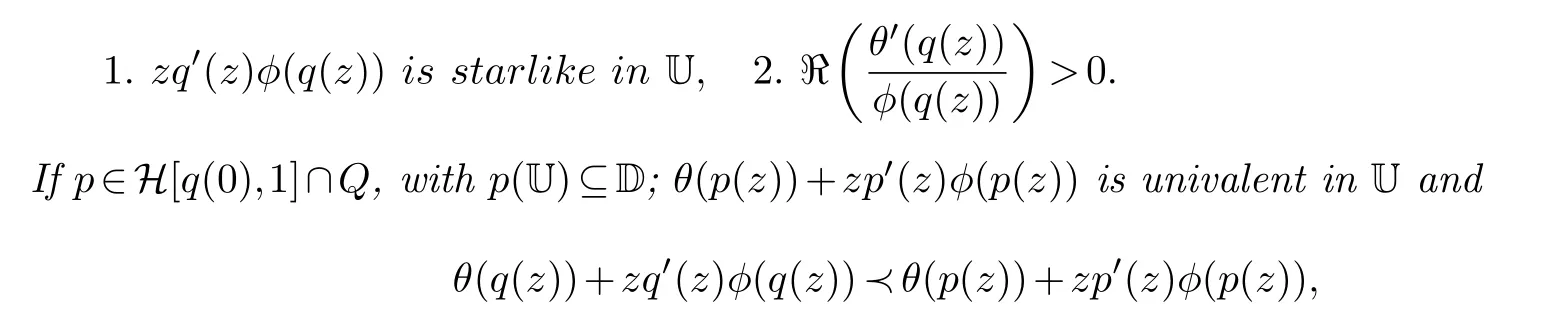
then q ≺p and q is the best dominant.

§3.The main relationships

We begin by stating the following inclusion relationship given by Theorem 3.1.

Theorem 3.1.Let0≤η<1and ϕ∈P with

Noting that (3.1) holds and q(z)≺ϕ(z)(z ∈U) we know that

Thus, an application of Lemma 2.2 to (3.15) yields

Proof.Suppose that

Thus, an application of Lemma (2.4) to (3.21) yields our desired result.

By means of (1.7), analogously, we can get following results.

Corollary 3.1.Let ρ<1and q be convex univalent inUwith

Thus, by means of (3.28) and Lemma 2.5, we readily get the assertion (3.27) of Theorem 3.7.

In view of (1.7) and Lemma 2.5, and by applying the method of proof of Theorem 3.7, we can get the following results.

andΦbe defined by(3.21)is univalent inU.If

and q is the best subordinant.

Finally,combining the above mentioned subordination and superordination results,we easily get the following sandwich-type results.

Corollary 3.6.Let q1,q2be convex univalent inUand ρ<1.Suppose that q2satisfies(3.16)

and q7,q8are,respectively,the best subordinant and the best dominant.