变分迭代法求解模糊分数阶Volterra积分微分方程*

陈 琴,陈豫眉

(西华师范大学,四川 南充 637009)

0 引言

分数阶微积分的应用十分广泛,电网络、分形理论、医学、生物学中的许多现象都可以用分数阶微积分的数学模型来描述[1-3]。但对现实系统建立数学模型时常有诸多不确定因素,使得数学模型中的一些参数无法确定。为了克服这个困难,通过在现实系统中引入模糊理论,用于描述现实中非精确的模糊现象。关于模糊分数阶积(微)分方程解的相关性质及其数值方法已有大量有效的研究成果。

Ahmad等[4]在Caputo意义下利用Schauder不动点定理研究模糊分数阶Volterra-Fredholm积分微分方程解的存在性和唯一性,并利用修正的Adomian分解法求解了该方程的数值解。Allahviranloo等[5]基于广义Hukuhara差分下的模糊Caputo导数研究模糊分数阶Volterra-Fredholm积分微分方程,使用Banach不动点定理证明了该方程解的存在性和唯一性。Hamoud[6]利用变分迭代法和Adomian分解法研究模糊Volterra-Fredholm积分方程的数值解,后利用修正的变分迭代法和修正的Adomian分解法求解了分数阶Volterra-Fredholm积分微分方程的数值解,并利用Schauder不动点定理证明了该方程解的存在性[7]。更多有关模糊积分微分方程解的相关性质及其数值解的研究可参见Ezzati、Hoa等人的文章[8-16]。

本文研究如下模糊分数阶Volterra积分微分方程

cDαu(x,r)=f(x,r)+g(x)u(x,r)+

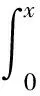
(1)

(2)

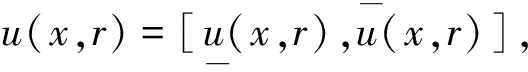
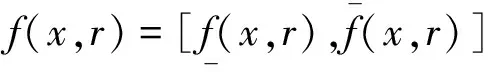
为源项函数,cDαu(x,r)是α阶Caputo导数,0<α≤1。

基于Ahmad[4]和Hamoud[6-7]等的研究,本文将利用Schauder不动点定理和Banach不动点定理分别证明模糊分数阶Volterra积分微分方程解的存在性和唯一性。变分迭代法[17-19]具有计算简单、精度较高等优点,且该方法较少用于模糊分数阶积分微分方程的数值求解。本文将利用变分迭代法求解方程(1)与方程(2)的数值解。

1 预备知识

定义1[21-22]设F(R)是R上的所有模糊集的集合,若u∈F(R)满足下列条件:

(1)u是正规的模糊集,即存在x0∈R,使得u(x0)=1;

(2)u是凸的,即对任意x1,x2∈R,ξ∈(0,1),有u(ξx1+(1-ξ)x2)≥min{u(x1),u(x2)};

(3)u是上半连续函数;

(4)u的支集的闭包[u]0∶cl{x∈R|u(x)>0}是紧的。

则称u是一个一维的模糊数。所有一维模糊数的全体称为一维模糊数空间,记为E。

定义2[23-25]定义两个模糊数w1,w2间的距离D为:

对任意的ε∈R,u,v,w,z∈E,距离D有如下性质:

(1)(E,D)是完备的度量空间;

(2)D(u,z)≤D(u,v)+D(v,z);

(3)D(u+w,v+w)=D(u,v);

(4)D(u+w,v+z)≤D(u,v)+D(w,z);

(5)D(εu,εv)=|ε|D(u,v);

定义3[25]模糊值函数f(t)的模糊Riemann-Liouville积分定义如下

其中,Γ是Gamma函数。

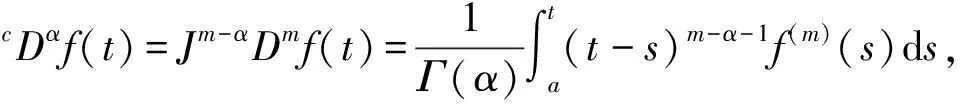
其中,m-1<α≤m,m∈N。

2 变分迭代法

1997年He[17-20]提出的变分迭代法是对一般Lagrange乘子法的改进,该方法可有效、简便、准确的求解一类线性和非线性问题。考虑如下分数阶方程:

cDαu+Mu+Nu=f(x)

(3)

其中,cDαu是α阶Caputo分数阶导数,M为线性微分算子,N为非线性项,f(x)为源项函数。

He方法的基本特征是构造方程(3)的修正泛函,即

(4)

通过变分迭代法求解方程(3)的步骤为:对式(4)分部积分得到Lagrange乘子λ(s),然后利用λ(s)和初始值u0得u(x)的逐次逼近解un(x),n≥0,即有如下变分迭代式:

(5)

下面给出另一种方法求解方程(3)。在方程(3)两端应用算子Jα得

u=R(x)-Jα[Mu]-Jα[Nu]

(6)

其中,函数R(x)是对源项函数f(x)积分和给定的初始条件所产生的项。

根据式(6)可得方程(3)近似解un(x),n≥0的变分迭代式

un+1(x)=R(x)-Jα[Mun(x)]-Jα[Nun(x)],n≥0

(7)

迭代式(5)与式(7)等价。本文将利用变分迭代式(7)求解模糊分数阶Volterra积分微分方程。

3 理论分析

设CF[a,b]表示[a,b]上所有连续模糊值函数空间。为了便于后续证明,给出以下假设:

H1g(x),f(x,r):[0,1]→E是连续有界函数。

H2 存在常数L,使得对任意的v1(x,r),v2(x,r)∈CF[0,1]满足下式:

D(B(v1(x,r)),B(v2(x,r)))≤LD(v1(x,r),v2(x,r))。

H3 对Y={(x,t)∈R×R:0≤t≤x≤1}上所有正连续函数的全体,存在数M,使得

3.1 存在性证明

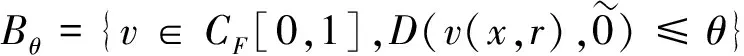
定义算子T:CF[0,1]→CF[0,1]

(1)首先通过以下三个步骤证明T是全连续算子。

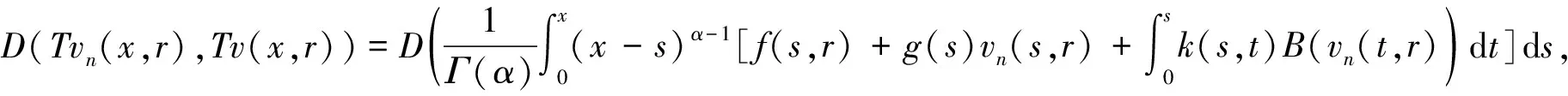
(8)

当n→∞时,由式(8)得

D(Tvn(x,r),Tv(x,r))→0

(9)

由式(9)可知T是连续算子。

(ii)T将有界集映射到CF[0,1]中的有界集。对任意的v(x,r)∈Bθ,有:

(10)

式(10)表明,对任意的v(x,r)∈Bθ,有Tv(x,r)∈Bγ。

(iii)T是等度连续算子。对任意的v(x,r)∈Bθ,x1≤x2,x1,x2∈[0,1]有:

D(Tv(x2,r),Tv(x1,r))

∶=P1+P2+P3

(11)

其中,

同理可得

当x1→x2时,将P1,P2,P3代入式(11)得

D(Tv(x2,r),Tv(x1,r))→0

因此得T是等度连续算子。结合上述(i)～(iii)结论和Arzela-Ascoli定理可知,T是全连续算子。

(2)需证明存在一个闭凸有界子集

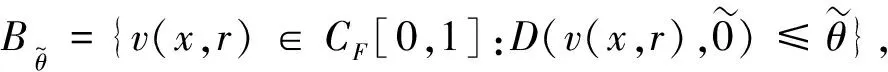
由式(10)得

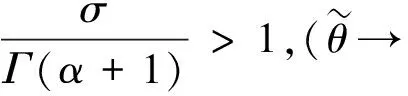
(12)

根据步骤(1)和步骤(2)的证明结果,由Schauder不动点定理知,至少存在v(x,r)∈CF[0,1],使Tv(x,r)=v(x,r)。存在性证明完成。

3.2 唯一性证明

证明 算子T与定理3.1定义的T相同,对任意的v(x,r),w(x,r)∈CF[0,1],x∈[0,1],有

D(Tv(x,r),Tw(x,r))≤

4 数值算例

例 考虑如下的模糊分数阶Volterra积分微分方程:

(13)

其中,

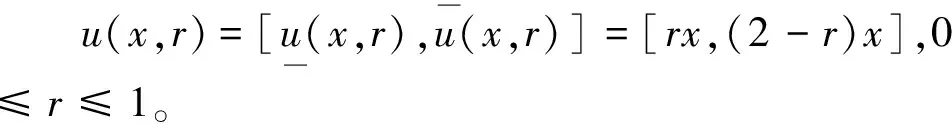
方程(13)等价于求解下列方程组

(14)

和

(15)

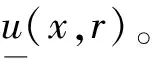
(16)

由式(16),得

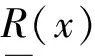
由式(7)得方程(16)的变分迭代式

…

5 结论

利用不动点定理证明了模糊分数阶Volterra积分微分方程解的存在性和唯一性。 变分迭代法求解该类模糊分数阶方程数值解,通过数值算例知变分迭代法对求解该类模糊分数阶方程可通过较少迭代次数得到方程的解,也说明变分迭代法求解该方程的有效性。 在接下来的工作中,将研究模糊非线性分数阶Volterra-Fredholm积分微分方程的稳定性,并利用修正的变分迭代法求解该类方程的数值解。