粒子加速器准直中测站坐标系高精度恢复方法

陈 哲,范百兴,邹方星,段童虎,黄 赫

(信息工程大学 地理空间信息学院,河南 郑州 450001)

粒子加速器作为“大国重器”,为物理、医学、材料科学等众多学科提供大量尖端研究手段[1]。为保证粒子按照设计轨道运行,对准直测量精度提出了很高要求[2]。准直测量工作的主要任务是将所有元件高精度安装至设计位置,实际测量过程中,需要在实验室进行元件预准直,即将多个元件安装在同一支架上,作为一个预准直单元,之后运输至粒子加速器隧道进行现场安装[3]。为提高测量效率、保证测量精度,中国散裂中子源[4]基于最小二乘原理,恢复激光跟踪仪测站坐标系,并设计制作专用吊车完成预准直单元安装;北京高能同步辐射光源[5]利用振动线完成磁铁磁中心引出,保证误差在10 μm内的情况下,基于多路激光“三高一低”的布设方案进行预准直[6],这与北京正负电子对撞机[7]均基于坐标转换原理,先恢复激光跟踪仪测站坐标系,再进行预准直单元安装。国内粒子加速器隧道控制网主要采用激光跟踪仪多测站架设建立三维控制网[2],由于高程方向误差累积明显,王小龙等[8]将大地水准面作为基准获取高程数据,建立附有高程约束的三维平差,实现高程方向误差累积的有效控制。

目前有关粒子加速器准直测量工作的研究,主要集中在元件预准直及高精度控制网的布设。针对测站坐标系的恢复问题,往往基于公共点坐标转换算法,依据最小二乘原理实现[3],并未顾及控制点在全局及激光跟踪仪测站坐标系下的点位误差。现有较为成熟且广泛应用的坐标转换方法主要有奇异值分解(singular value decomposition,SVD)法[9]、四元数法[10]、正交Procrustes法[11]、罗德里格矩阵法[12]、加权整体最小二乘(weighted total least squares,WTLS)法[13]等,均根据公共点坐标距离平方和最小构造目标函数,基于最小二乘算法获取最优解。其中,SVD法与正交Procrustes法理论简单易实现,但当公共点过于密集时,旋转矩阵的正确性无法保证;四元数法基于线性微分方程,获取旋转矩阵,运算简单,且在求解过程中,不存在奇异点;罗德里格矩阵法稳定性强,但计算过程复杂,不易实现。文献[14]研究表明,上述方法在进行坐标转换过程中,精度差值均在2 μm内,相差较小,但均未考虑点位误差对转化精度的影响。WTLS法顾及观测值及系数矩阵的随机误差,同时考虑到系数矩阵中各随机元素的精度不同,在一定程度上提高了转换精度,但无法顾及旋转矩阵正交约束条件。针对此问题,本研究构建了顾及点位统计性质的测站坐标系恢复模型,在考虑旋转矩阵正交约束条件的基础上,利用李代数思想对已构建的数学模型进行线性化和迭代计算,并通过仿真与实测实验,验证了本研究方法的正确性及有效性,相较于传统测站坐标系恢复方法精度更高。

1 测站坐标恢复

1.1 测站坐标恢复及元件安装原理

粒子加速器设计过程中,需确定设备基准点在待安装全局坐标系中的理论坐标值。目前,全局坐标系作为准直测量的全局基准,主要利用GNSS、陀螺全站仪、水准仪等进行观测,通过布设一级地面网提供绝对位置参考,因控制网的精度逐层增高,只保留必要起算数据控制二级隧道网[15];利用激光跟踪仪、水准仪等构建附加约束的三维控制网,提供高精度相对定位[16]。隧道网控制点分布在隧道内截面方向的墙面、地面和顶面,如图1所示。

(1)

εi=Xi-k(Rxi+T)。

(2)

其中:R、T分别为控制点在两坐标系下的3×3旋转矩阵、3×1平移矩阵;εi为3×1的测站坐标系恢复残差矩阵,考虑到激光跟踪仪的高精度测距能力,取k=1。

预准直时,采用水准仪、经纬仪、激光跟踪仪、电子水平仪、振动线技术等,确定元件机械重心与物理重心的关系,并关联至元件基准点上[17]。此时,利用激光跟踪仪测量待安装元件基准点yi,按照式(3),基于已恢复的测站坐标系,将元件基准点坐标转换至全局坐标系下,计算设计位置的偏差并进行准直调整。

Yi=Ryi+T。

(3)

其中:Yi、yi分别为待安装元件的基准点在全局与激光跟踪仪测站坐标系下三维坐标。

1.2 构建数学模型

粒子加速器二级隧道控制网通过多测站联合平差解算(Xi,Yi,Zi),(xi,yi,zi)依据激光跟踪仪球坐标测量原理获取,如图2所示。

图2 多测站联合测量及球坐标测量原理

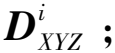
(4)

其中:Si、Vi、Hi分别为距离、天顶距、水平角观测值。对式(4)取全微分,得到系数矩阵K。按照方差-协方差传播定律计算方差-协方差矩阵

(5)

顾及控制点在全局坐标系和测站坐标系下点位误差对式(1)中R、T计算结果准确度的影响,根据方差-协方差传播定律确定权阵

(6)

扩展式(2)为:

(7)

此时,式(7)中涉及的极小值问题可以转化为:

(8)

构建数学模型,则求解问题可以转化为解算方程:

wi(Xi-Rxi-T)=0。

(9)

1.3 线性化方法

非线性方程组的求解分为最优化迭代和智能优化方法,其中最优化迭代计算依赖初值的选取,且易陷入局部最优;智能优算法面临求解精度不高,且针对特定问题无法保障解算性能等问题。相对于非线性方程,线性方程的求解技术更加成熟[18],目前主要依据最小二乘算法实现。针对坐标转换问题,扩展至加权整体最小二乘算法,但该算法推导繁琐、不便于理解,坐标转换精度影响因素不直观,且无法顾及旋转矩阵正交约束条件。因此提出李代数理论,李群(SO(3))是具有群结构的光滑流形,李代数是其单位元处的正切空间,旋转矩阵属于SO(3)[19]。根据李代数理论,将目标函数线性化,之后进行迭代计算,获取未知参数高精度解算结果。

旋转矩阵R通过李代数指数映射和幂级数展开获得:

(10)

此时式(9)可表示为:

(11)

(12)

此时,式(11)可表示为:

(13)

1.4 迭代算法

图3 计算流程图

(14)

2 误差分析

(15)

(16)

将式(16)代入式(15)得:

(17)

根据式(10)和简化式(17)可得:

(18)

式(11)可变换为下列方程组:

(19)

wiCW=wie,

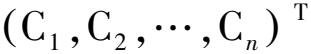
(20)

由此可得,解算结果误差由控制网点平差解算算法、观测误差、测站坐标系下观测误差及控制点布局决定。测站坐标系恢复过程中,控制点在全局和测站坐标系下三维坐标精度、空间布局、数目等因素均影响解算结果。

3 仿真分析

分别利用WTLS方法和本研究方法进行数据处理。对比两种方法解算所得的旋转矩阵、平移矩阵元素及与其真值的差值,结果如图4所示。相较于WTLS算法,本研究提出的线性迭代解法所得的旋转、平移矩阵精度明显提高,其中旋转矩阵元素最多提高2 μm,平均提高1 μm;平移矩阵最大提高4.9 μm,平均提高1 μm。通过改变公共点个数计算两种方法对应的均方根误差(root mean square error,RMSE),如表1所示。

表1 不同公共点按照WTLS和本研究方法的RMSE

图4 不同方法解算的旋转、平移矩阵元素及与其真值的差值

由表1中可知,相较于WTLS算法,本研究方法在进行测站坐标系恢复时,RMSE明显降低,最少降低4 μm,最多降低42 μm,在3～8个公共点的情况下平均降低18 μm。仿真结果验证了本研究方法的正确性。

4 实测验证

在温度相对稳定的某光源直线段内利用AT960激光跟踪仪进行多测站观测,保证相邻测站至少存在3个公共点。如图5所示,实验前仪器经过计量检定符合标称精度。

图5 测站及控制点分布

以第一测站坐标系为全局坐标系,按照多测站联合平差方式获取控制点全局坐标[22]。在直线段某磁铁附近,自由设站架设激光跟踪仪,对已知全局坐标的控制点进行观测,得到25个全局控制点在测站坐标系下的三维坐标。张皓琳等[23]研究表明,在进行坐标转换过程中,随公共点个数增加,转换误差减小,但当公共点超过6个时,转换精度改善不明显。为兼顾测量精度和实际测量过程中测站坐标系恢复效率,选择8个公共点进行测站坐标系恢复,8个公共点在全局及测站坐标系的三维坐标如表2所示。

表2 8个公共点在全局及测站坐标系的三维坐标

分别利用WTLS方法和本研究方法对两组坐标进行处理,恢复自由设站激光跟踪仪测站坐标系,得到两种方法的RMSE,如图6所示。相较于WTLS算法,本研究方法在进行测站坐标系恢复时,RMSE明显降低,其中最少降低27 μm,最多降低36 μm,在3～8个公共点的情况下平均降低30 μm,减小了54.5%,验证了本研究方法与传统方法相比恢复精度明显提高。当公共点大于6时,解算精度趋于稳定,与文献[23]结论一致。将测站坐标系除公共点外17个控制点的三维坐标,分别利用WTLS与本研究方法恢复的测站坐标系参数转换至全局坐标下,计算坐标分量与全局坐标系下三维坐标分量之差,结果如图7所示。

图6 不同公共点按照WTLS和本研究方法解算所得RMSE

图7 两种方法转换后三维坐标分量与全局坐标分量之差

由图7可知,利用WTLS方法恢复测站坐标系,将非公共点三维坐标转换至全局坐标,转换后各点坐标分量与全局坐标同一点坐标分量的差值最大为22 μm,最小为2 μm,平均为8 μm。根据本研究方法恢复测站坐标系,非公共点转换后各点坐标分量与全局坐标同一点坐标分量差值最大为12 μm,最小为0.5 μm,平均为5 μm。实测结果表明,依据本研究方法进行测站坐标系恢复,顾及点位位于测站及全局坐标系下点位误差的同时,还考虑旋转矩阵的正交约束条件,比WTLS方法恢复的测站坐标系精度更高。

仿真分析和实测实验验证了本研究提出的线性迭代算法恢复测站坐标系的正确性,同时依据激光跟踪仪测站坐标系恢复的RMSE,以及基于已恢复的测站坐标系参数,将测站坐标系三维坐标转换至全局坐标系,得到与全局坐标系三维坐标分量的差值。结果表明,针对测站坐标系恢复问题,考虑点位在测站及全局坐标系的点位误差基础之上还顾及旋转矩阵正交约束条件,引入李代数理论迭代计算恢复测站坐标系,理论更加严密、恢复精度更高,对实际测量工程具有实用价值。

5 结束语

本研究在激光跟踪仪测站坐标系恢复过程中,顾及点位在测站及全局坐标系下的点位误差和旋转矩阵的正交约束条件,依据李代数思想推导线性迭代算法,实现了粒子加速器准直过程中激光跟踪仪测站坐标系高精度恢复的目的。同时,定性分析了影响测站坐标系精度恢复的因素。在此基础上,分别利用本研究方法与传统方法处理仿真与实测数据,验证了本研究所提出的线性迭代算法的正确性,并在一定程度上提高了测站坐标系恢复精度,为实现元件高精度安装提供了保障。研究还发现,测站和点位的布局、数目以及实测过程中大气温度、湿度、压强、反射靶球球心偏差和入射角误差等均影响数据的解算结果,后续可对此问题进一步研究。