融合阈值法的贝叶斯压缩感知振动信号重构
张笑华,刘婷婷,陈富强,何 鹏,阮翔愉
(1.福州大学 土木工程学院,福建 福州 350108; 2.福建建工集团有限责任公司,福建 福州 350001;3.中国建筑第二工程局有限公司,北京 101149; 4.江苏东华测试技术股份有限公司,江苏 泰州 214500)
结构健康监测是利用采集到的数据,通过一系列时域[1]、频域[2]或者小波域[3-4]的信号处理方法,来感知、评估和预警结构的状态。根据传统的奈奎斯特采样定理,结构监测数据采样频率必须超过信号最高频率的两倍才能确保信号不失真,从而带来结构实时监测的海量数据,增加监测数据的传输和存储压力。压缩感知(Compressed Sensing,CS)理论的出现为SHM信号的采集和分析提供了一种全新的方案[5-6]。该理论对可压缩信号以远低于奈奎斯特采样率的方式进行采样,并利用重构算法恢复原始信号。鉴于CS理论的优越性,学者们将其应用在图像恢复[7]、图像优化[8]、光学成像[9],磁共振成像[10],无线传感网络数修复[11]等领域。
CS理论的应用前提是信号具有稀疏性。而土木工程结构的动力响应信号在频域、小波域或者其它变换域上具有近似稀疏的特性,因此不少学者将CS理论应用于结构健康监测中。Bao等[12]利用CS理论压缩黄河公路大桥结构健康监测系统采集的加速度数据,并与基于小波变换和霍夫曼编码方法采集的加速度数据进行比较,分析CS的数据压缩能力。结果表明,相较于其它方法,CS能将振动数据有效压缩,减少了数据采集量,节约了数据传输与存储的成本。Peckens和Lynch[13]设计了一个仿生CS方法,利用受耳蜗激发的传感器采集结构健康监测数据,实时对数据进行高压缩,提高数据的传输效率。季赛[14]提出基于压缩感知的无线传感结构健康监测方法,该方法利用高斯随机矩阵将航空铝板的振动响应信号从高维投影到低维空间中,以此实现信号压缩采样,最后再采用改进的正交匹配追踪算法对稀疏信号进行重构。张笑华等[15]通过增加观测矩阵和稀疏基的不相关性对观测矩阵进行优化,以这种方式提高桥梁结构健康监测的压缩感知动力响应信号重构精度。这些研究成果表明压缩感知理论可以运用在结构健康监测数据压缩和重构上。重构算法的选择会影响原始信号重构的精度。已有的重构算法可以分为两类:凸优化算法和贪婪算法。凸优化算法需要对目标函数进行求解,而这个过程可能会非常耗时。贪婪算法虽然速度快,但是它的精度不如凸优化算法高。因此,为了解决这些问题,学者们开始探索新的压缩感知重构算法,提出了基于贝叶斯框架的重构算法[16-17]。
Ji等[16]首次将贝叶斯理论应用到压缩感知中,使压缩感知重构问题与稀疏贝叶斯学习方法相结合,提出一种贝叶斯压缩感知(Bayesian Compressive Sensing,BCS)算法,并阐述了BCS的理论分析及数学推导。Huang等[17]利用BCS算法来重构近似稀疏信号,并使用北京国家游泳中心(水立方)和台湾高雄市的一座斜拉桥的结构健康监测系统的真实信号来验证算法的性能。Ji等[18]在BCS的基础上设计了一种多任务贝叶斯压缩感知方法,充分利用了信号之间的统计相关性,基于多任务的稀疏贝叶斯学习理论将一个信号通过不同观测矩阵进行多次观测,从多个不同的低维观测中联合重构出原始信号,以此降低重构信号的不确定性。马云飞等[19]提出了一种旋转机械振动信号贝叶斯压缩重构方法,通过利用拉普拉斯先验及稀疏块相关性来增强信号的稀疏性,从而提高压缩感知的效率和精度。
由于噪声的影响,结构健康监测的振动响应信号稀疏性较差,影响了原始响应信号重构的精度。鉴于此,在BCS的基础上,引入小波阈值减噪的思想,提出一种融合阈值法的贝叶斯压缩感知振动信号重构方法。针对土木工程结构测量信号具有稀疏性差和噪声干扰大的特点,采用阈值法增强信号的稀疏度,以改善后续响应重构的精度,通过BCS压缩信号并重构原始信号,解决桥梁结构健康实时监测海量数据造成存储和传输成本高的问题。
1 贝叶斯压缩感知
根据压缩感知理论,N×1的一维信号x可以线性表示为:
x=Ψθ
(1)
式中:Ψ是N×N的稀疏正交基;θ称为K稀疏向量,K为稀疏度。
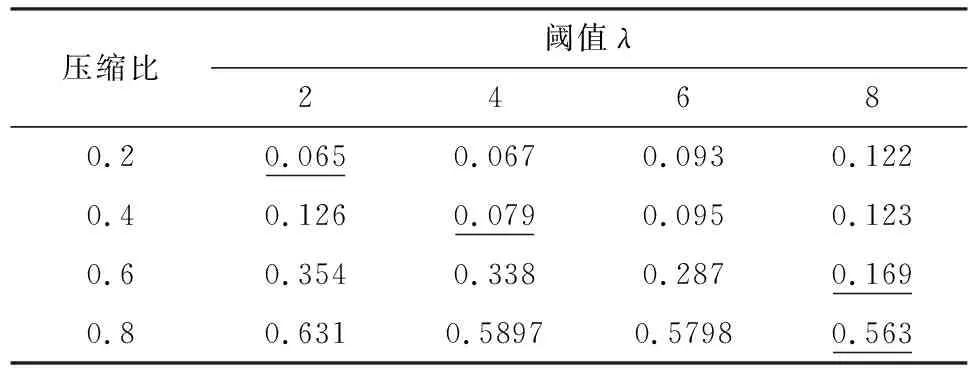
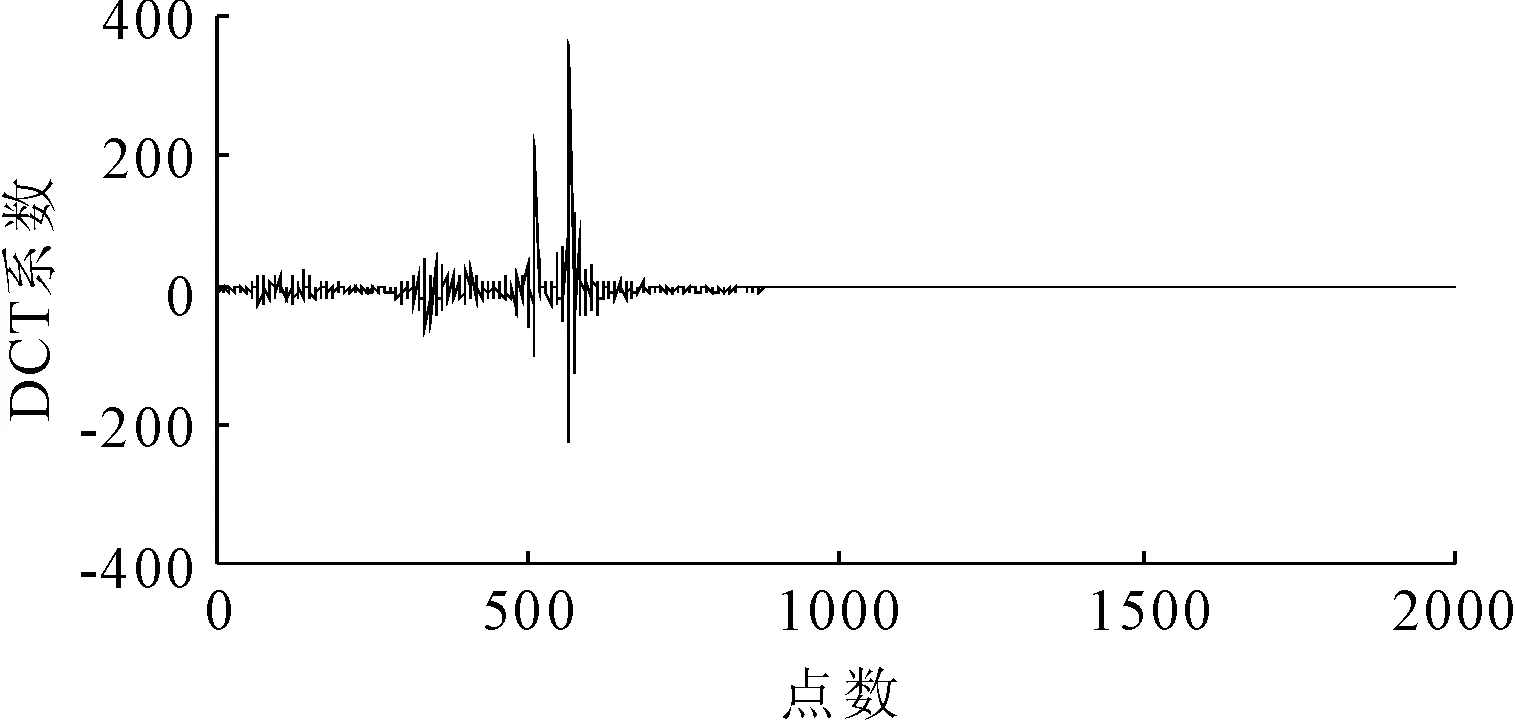
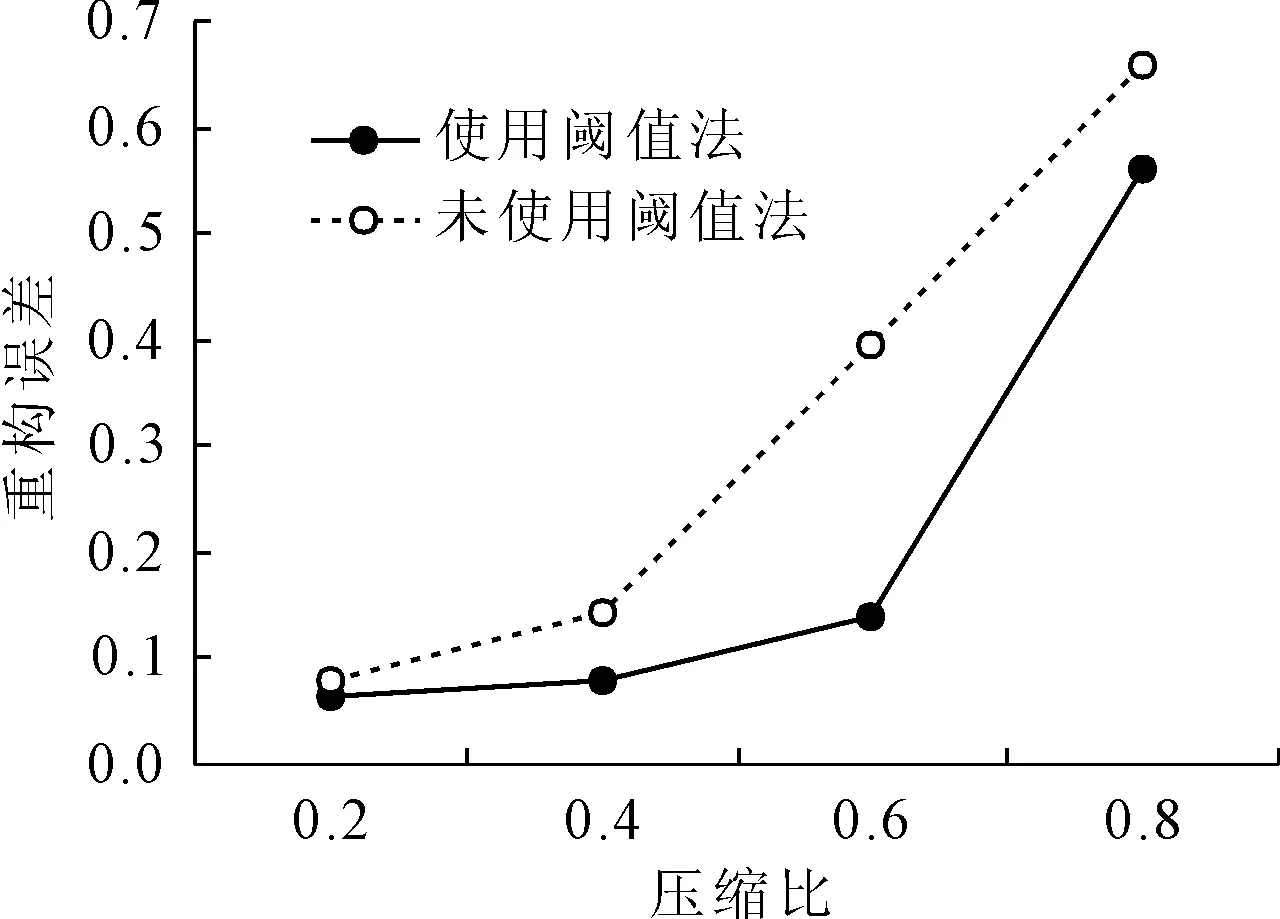
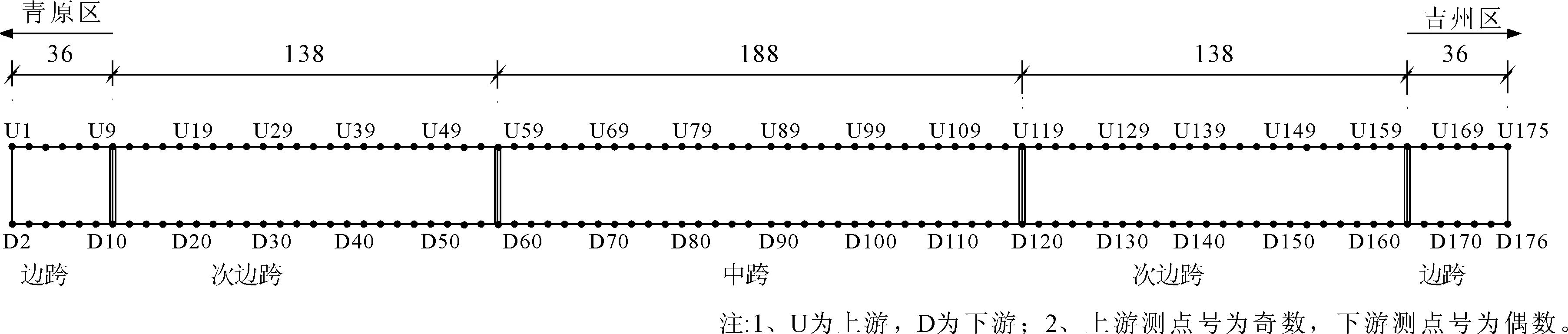
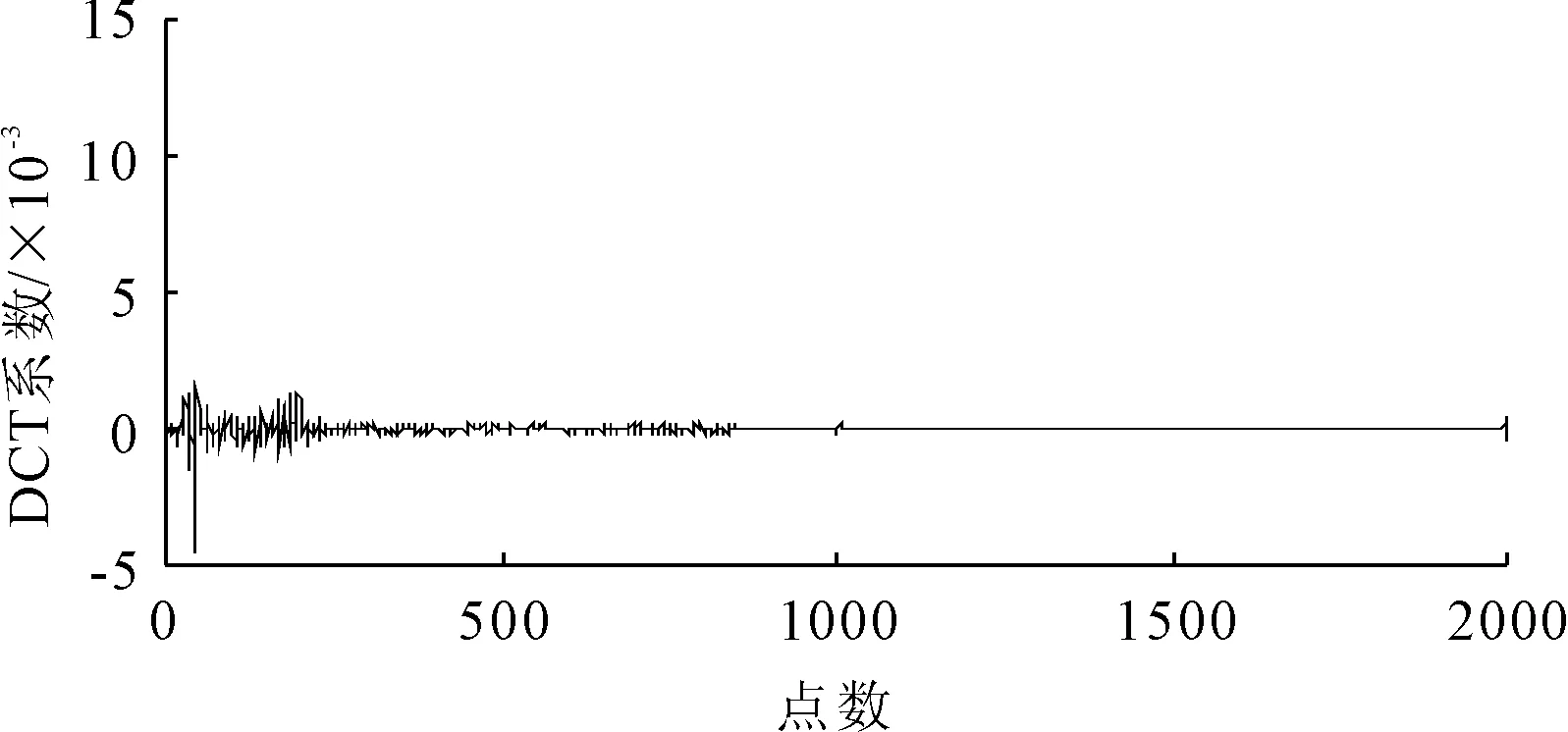
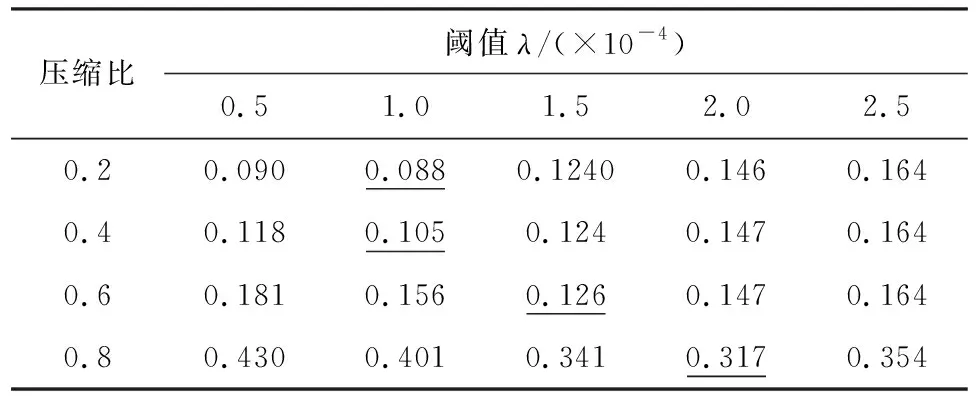
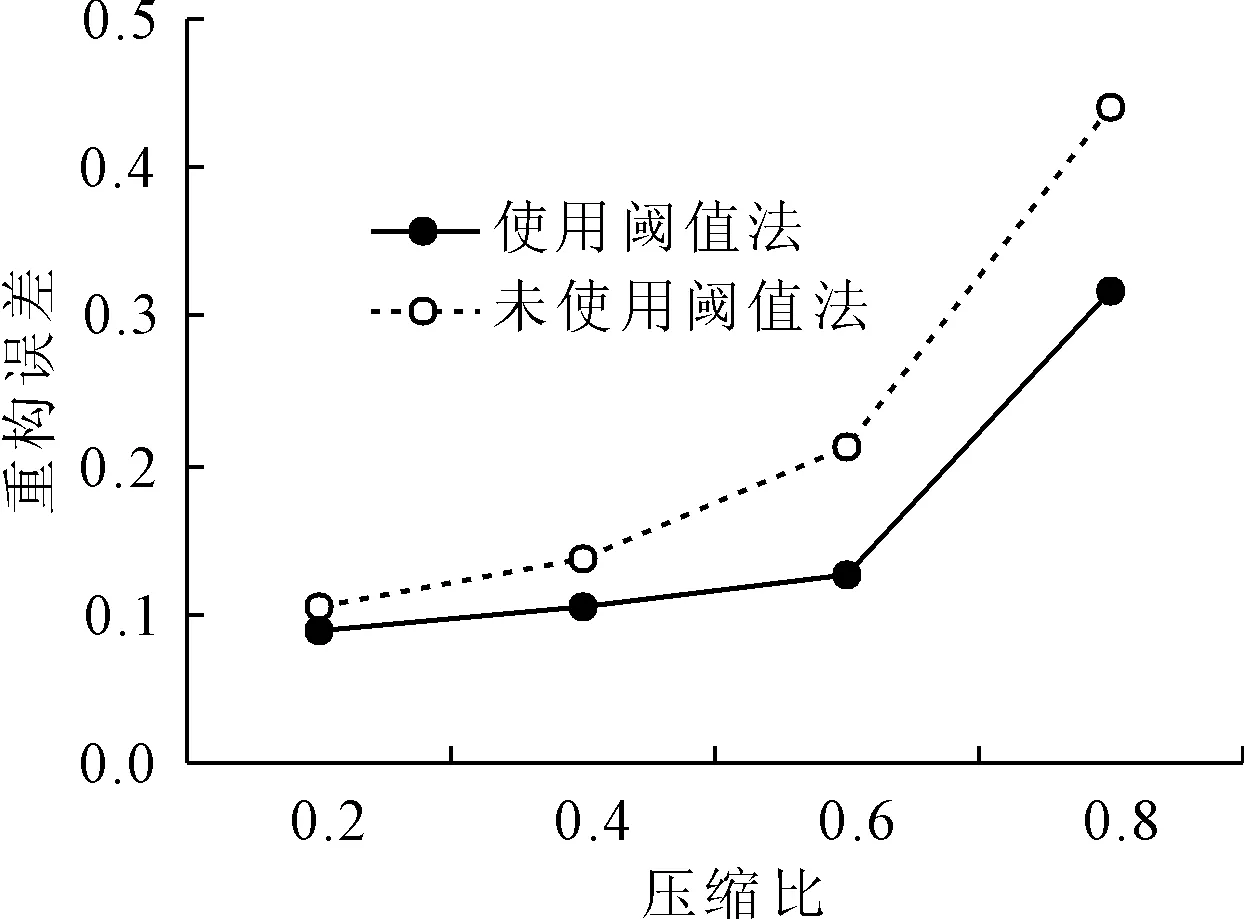
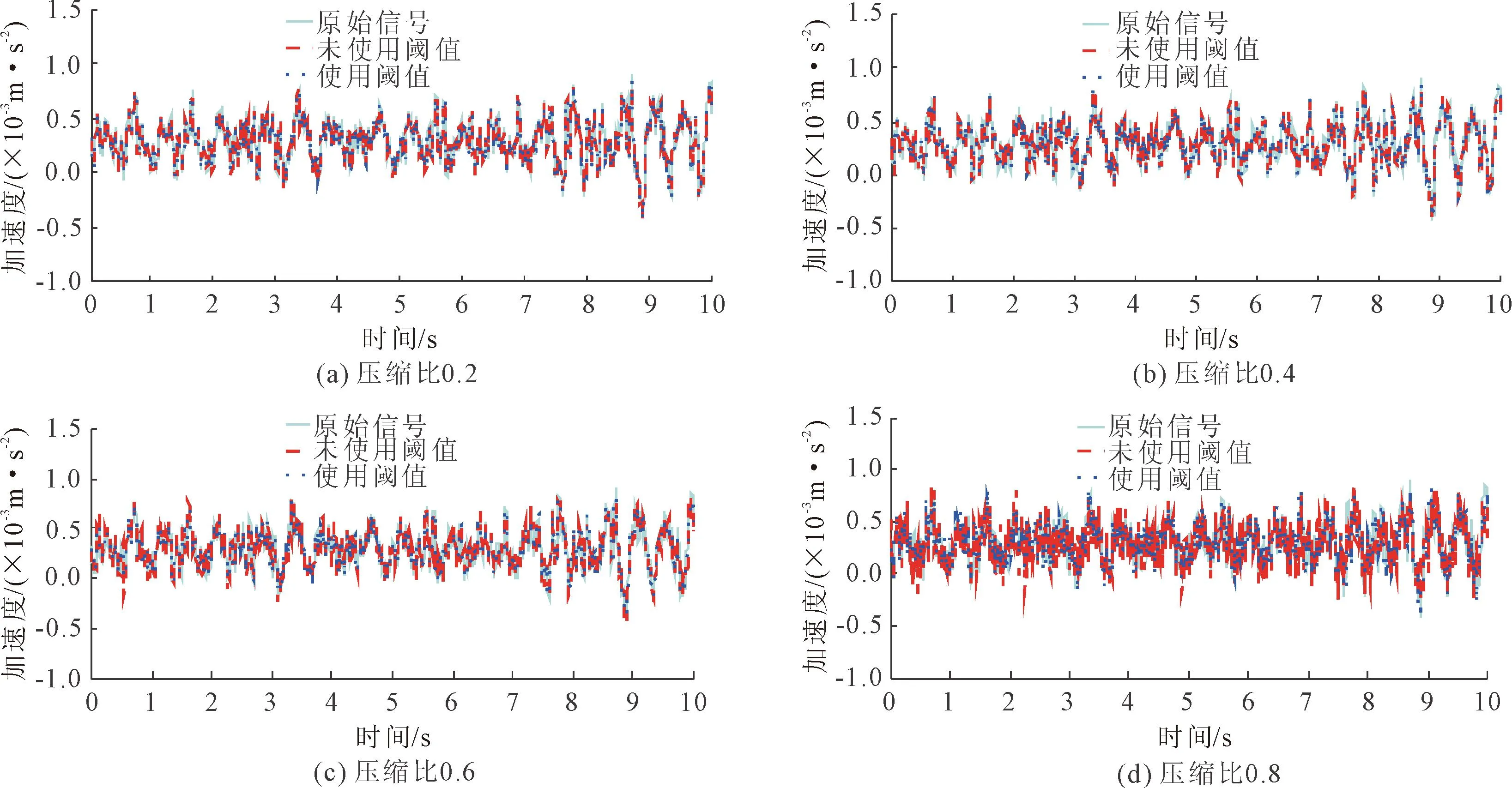
信号通过M×N维的观测矩阵Φ(M y=ΦΨTx=Φθ (2) 将稀疏向量θ分解为向量θs与向量θe两项,式(2)改写为: y=Φ(θs+θe)=Φθs+ne (3) 式中:θs的N-K个元素对应的是K稀疏向量θ中N-K个值最大的元素,其余K个元素为0;θe的K个元素对应的是K稀疏向量θ中K个值最小的元素,其余N-K个元素为0,ne=Φθe。 由于观测矩阵Φ是随机的,根据中心极限定理,ne中的元素可视为均值为零、方差为σ2的高斯噪声。则y的高斯似然模型为: (4) 由此,将传统的压缩感知理论中求解稀疏权重系数问题转变成稀疏情况下θ稀疏约束的线性回归问题[20]。 (5) 为了让噪声的超参数和信号的超参数相匹配,将噪声的超参数设为噪声方差的倒数,即: α0=1/σ2 (6) 定义超参数α和α0均服从Gamma分布以简化计算。对超参数α进行边缘分布计算,得到稀疏向量θ的概率分布函数: (7) 式中:a、b是Gamma参数。 根据上面所确定的先验概率分布和观测信号y可通过贝叶斯准则求得后验概率分布为: p(θi|yi,α)= (8) 其中 (9) (10) 式中:对角矩阵A=diag(α1,α2,…,αN)。 BCS信号重构的主要任务就是估计先验超参数α,然后根据式(9)求出稀疏向量μ,也即重构的稀疏向量,然后可恢复所对应的原始信号。 (11) (12) 式中:C-i表示去掉第i个相关基φi后的协方差矩阵C,后项就是去除的部分。 通过上述计算可以对最大化后验概率密度函数的似然对数L(α,α0)进行分解: L(α,α0)=L(α-i,α0)+ (13) (14) (15) 式中:si被称为“稀疏因子”,用来判断基向量φi是否与模型中剩余所有基向量重叠;qi被称为“质量因子”,用于矫正去除基向量φi后对模型误差。 对式(13)进行求导,使其对αi的导数为零可得: (16) (17) (18) 其中B=α0I。根据上式得到的参数Sm、Qm可以用来更新“稀疏因子”si及“质量因子”qi,其数学表达式为: (19) 由上式可知,当αi=∞时,sm=Sm,qm=Qm。 压缩感知理论的应用需要先将实际中原信号通过稀疏变换转化为稀疏向量,然后再利用压缩感知的原理进行采样和重构。信号的稀疏度会影响信号的重构效果。在采样条件不变的情况下,信号的稀疏度越高,原始信号被高精度地恢复的可能性就越高。理想的稀疏信号是指在大部分时刻里信号取值为零,而在少数时刻里信号的幅值相对较大。 而实际上,由信号x经稀疏变换得到的稀疏向量θ并不具有理想的稀疏性。经稀疏变换得到的稀疏向量θ虽在少部分时刻里有较大的幅值,不过在很多时刻里也具有较小的幅值,导致信号的重构精度和重构概率下降。因此为了提高重构概率和重构精度,通过引入小波阈值去噪方法来提升稀疏向量θ的稀疏程度[22]。其基本思想是:根据稀疏向量θ的信号特征,引用硬阈值法[23],对稀疏向量θ进行阈值处理,即根据不同信号在不同压缩比下设置不同的阈值,比较稀疏向量θ与阈值的大小,将低于阈值的系数置零,高于阈值的系数保持不变。其数学表达式如下: (20) 通过阈值处理,不仅可以很好地保留信号的局部特征,而且在相同采样条件下提高信号重构概率和重构精度。 融合阈值法的贝叶斯压缩感知振动信号重构算法步骤总结如下: 步骤1:选取适当的稀疏基Φ,按照式(1)把信号x在稀疏基Ψ上做稀疏表示,获取稀疏向量θ,其中Ψ是N×N的稀疏正交矩阵。 步骤5: 计算均值μ及协方差Σ,同时利用式(17)与(18)初始化sm与qm。 步骤8: 更新噪声方差,根据式(9)和式(10)更新均值μ和协方差Σ,同时根据式(17)和式(18)更新sm和qm。 步骤9: 判断算法是否满足收敛条件,如满足则结束计算,否则重复执行步骤4~步骤9。 为了验证融合阈值法的贝叶斯压缩感知振动信号重构算法的有效性和适用性,以实验室简支外伸梁和吉安大桥为例,模拟振动信号的压缩和重构。 简支外伸梁全长4 m,横截面尺寸为50 mm×15.65 mm。梁的弹性模量E=205 GPa,密度为7 780 kg/m3,泊松比为0.3。将梁先安装在滚柱轴承和铰链轴承上,然后轴承底板用四个螺栓固定于混凝土块顶部厚钢板上,如图1所示。试验中在梁的端部安装了B&K4374型加速度计,利用LDS V451励磁器、B&K信号发生器和LDS PA500功率放大器相结合以产生随机激励,激励点位置设置在离铰支座0.5 m的位置,如图2所示。加速度响应通过数据采集系统KYOWA EDX-100A 以500 Hz的采样频率采集。其它有关试验的详细情况可见参考文献[24]。 图1 简支外伸梁 图2 激励位置和传感器位置 为了评价信号的重构效果,定义重构相对误差为: (21) 重构相对误差ξ越小,则重构精度越高。 此外,在压缩感知的数据压缩中用到了压缩比的概念,定义压缩比为: (22) 式中:M是观测信号即压缩信号的长度,N代表原始信号的长度,均用数据个数来表示。 稀疏基与观测矩阵分别采用离散余弦基和高斯随机矩阵,并考虑0.2、0.4、0.6和0.8等四种压缩比。 在确定阈值大小时,先对采集的加速度信号做稀疏变换,变换后的DCT系数如图3所示。依照DCT系数经过试算,为了最大程度保留信号的有用信息,所选取的阈值应小于10,这里选取阈值为2、4、6、8,然后利用本文提出的算法对测量的加速度振动响应信号进行压缩感知重构,重构误差如表1所示。阈值选取不同,对应压缩信号的稀疏度也不同,阈值越大,幅值较小的信号被舍弃越多,信号的稀疏度也越大。压缩比较小时,测量信号保留较多,重构的响应精度较高,则可取较小阈值来稀疏化信号。压缩比较大时,测量信号保留较少,为了更好地恢复原始信号,可以取较大的阈值,以保留更多的稀疏信号,以提高重构精度。表1中带下划线的误差是不同压缩比下取不同阈值重构后的最小误差,对应的阈值可定为该压缩比下的最合适阈值。因此0.2、0.4、0.6和0.8的压缩比下分别选取阈值2、4、8和8用于后续的压缩感知响应重构。 表1 振动信号重构误差(实验室简支外伸梁) 图3 加速度信号的DCT系数 为了对比分析,将融合阈值法的贝叶斯压缩感知信号重构结果与未使用阈值化处理的重构结果进行对比,对比结果如图4所示。 图4 使用阈值前后的信号重构误差(实验室梁) 从图4可见,用提出的方法重构的结果相比于未使用阈值法得到的重构结果,误差更小。其时程信号对比如图5所示,当压缩比较低时,如不大于0.4时,未使用阈值的与使用阈值的重构时程信号都与原始信号吻合良好;但压缩比逐渐增大时,未使用阈值的重构时程信号误差越来越大,而用本文提出的融合阈值法的贝叶斯压缩感知振动信号重构法得到的重构响应仍与原始信号吻合良好。 吉安大桥位于江西省吉安市,位于赣江水道之上,如图6所示。该桥为钢管混凝土中承式拱桥,全长536 m,主桥桥面总宽28 m,跨径为36 m+138 m+188 m+138 m+36 m。为了测试桥面竖向的自振特性,在桥吊杆和立柱连接处的上下两侧的桥面上分别选取88个测点,共176个测点,其测点的平面布置图如图7所示。其中测点布置的传感器选用941-B型伺服加速度传感器,传感器检测到的环境振动加速度信号经过INEV-16和IEVN-9多功能放大器的放大和滤波后,由32通道东方科卡数据采集仪进行采集,并将采集到的数据保存到电脑的硬盘中。现场采用的采样频率为200 Hz,采样20 min,每个通道采样的加速度时程数据为200×20×60=240 000个。其它有关试验的详细情况可查看文献[25]。 图6 吉安大桥 图7 传感器测点布置(单位:m) 选取中跨下游D90测点某段10 s的加速度时程信号作为原始信号作为研究对象,对其进行压缩采样并重构。其中稀疏基依旧采用离散余弦基,观测矩阵也选用高斯随机矩阵,同样考虑0.2、0.4、0.6和0.8等四种压缩比。对选取的数据进行稀疏变换,经变换后的DCT系数如图8所示。 图8 D90测点加速度信号的DCT系数 依照DCT系数并经过试算,为了保留信号的有用信息,选取的阈值不宜大于4.0×10-4。因此选取阈值为0.5×10-4、1.0×10-4、1.5×10-4、2.0×10-4、2.5×10-4对振动信号进行阈值化处理,然后再使用提出的重构算法重构原始信号。重构结果如表2所示。表中带下划线的数值是不同压缩比下取不同阈值重构后的最小误差,对应的阈值可定为该压缩比下的最合适阈值。因此0.2、0.4、0.6和0.8的压缩比下分别选取阈值1.0×10-4、1.0×10-4、1.5×10-4和2.0×10-4用于后续响应重构。 表2 振动信号重构误差(测点D90) 图9是融合阈值法的贝叶斯压缩感知信号重构误差与未使用阈值化处理的压缩感知响应重构误差的对比图。从图9可以看到,在各压缩比下,利用融合阈值法的贝叶斯压缩感知重构算法得到的结果精度均高于未使用阈值法的结果,尤其是在高压缩比的情况下。加速度振动响应信号的时程信号对比图如图10所示。从图10可以看出,经过阈值化处理后的重构信号与原始时程信号吻合更加良好。 图9 使用阈值前后的信号重构误差(吉安大桥) 图10 响应信号时程对比(吉安大桥) 针对结构健康监测因海量数据导致数据存储和传输压力大以及监测信号受外界环境噪声影响导致信号稀疏性较差的问题,提出了一种融合阈值法的贝叶斯压缩感知振动信号重构算法。主要结论如下: (1) 提出了融合阈值法的贝叶斯压缩感知振动信号重构算法。根据经稀疏变换所得到的稀疏向量的信号特征,引用硬阈值法,将低于阈值的系数置零,高于阈值的系数保持不变,以此实现对稀疏向量的阈值化处理,从而改善后续的原始信号重构精度。 (2) 提出的算法优于未使用阈值的算法。实验室简支外伸梁和吉安大桥的试验数据分析结果表明,在各压缩比下,利用融合阈值法的BCS算法重构振动信号的结果优于未使用阈值法的BCS算法得到的结果,尤其是高压缩比下。 (3) 使用融合阈值法的BCS算法重构得到的时程信号与原始时程信号吻合更加良好,表明融合阈值法的贝叶斯压缩感知振动信号重构算法是实现用少量采样数据恢复较为准确原始信号的有效方法。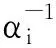
2 快速超参数估计方法
3 基于阈值法稀疏化振动信号
4 融合阈值法的贝叶斯压缩感知振动信号重构算法步骤
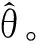


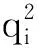
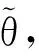
5 试验验证
5.1 实验室试验概况


5.2 简支外伸梁信号重构及数据分析
5.3 吉安大桥简介及试验概况

5.4 吉安大桥信号重构及数据分析
6 结 论

