化归与转化思想在立体几何题中的应用

陆晓峰

(海南省三亚市第一中学)

从某种意义上来看,解答数学问题的过程就是化归与转化的过程,即化未知为已知,化陌生为熟悉.立体几何题也不例外,化归与转化思想在立体几何题求解中有着广泛的应用.下面就其应用条件、适应类型举例分析.

1 空间化平面

空间化平面是处理立体几何题的重要方式之一,空间几何体是由平面几何图形构成的,在处理某些空间问题时,可将其侧面展开为平面图形,从而结合平面图形的有关性质解决问题.

例1 如图1所示,在顶点为S,底面圆心为O的圆锥中,AB是底面圆的直径,C是圆O上不同于A,B的点,且SO＝OB＝1,BC＝2,点P在线段SB上,则PO＋PC的最小值为_________.

图1

因为SO＝OB＝1,且SO⊥AB,所以△SOB为等腰直角三角形,SB＝2,所以SC＝2,即SB＝SC＝BC,△SBC为等边三角形.将△SCB绕SB旋转至与平面SOB共面的位置,如图2 所示.当O,P,C三点共线时,PC＋PO取得最小值.在等边△SBC中,在等腰Rt△SOB中,所以PO＋PC的最小值为

图2

空间问题平面化是解答立体几何中最短距离问题的常用方法,利用平面化将式中涉及的线段置于同一平面内,再结合平面几何知识求解.

2 整体化局部

当我们整体地看待某一个几何体时,其性质并不能很好地体现,造成解题困难,此时可考虑将其分割为几部分,再对每个部分逐一击破.

例2 已知F是正方体ABCD-A1B1C1D1的棱AA1上的动点,平面BFD1与棱CC1交于点E.对于任意的点F,四棱锥B1-BED1F的体积是否为定值?

如图3所示,连接BD1,将四棱锥B1-BED1F分割为三棱锥D1-BFB1和三棱锥D1-BEB1.

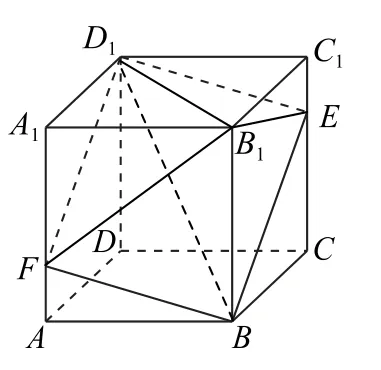
图3

对于三棱锥D1-BFB1,底面△BFB1的面积为定值,高为点D1到平面ABB1A1的距离,即

正方体的棱长,为定值,故其体积为定值.同理,三棱锥D1-BEB1的体积为定值,所以VB1-BED1F＝VD1-BB1F＋VD1-BB1E为定值.

本题中四棱锥B1-BED1F的底面和高均不确定,若直接求解,较为烦琐,将其分割为两个三棱锥,而三棱锥的体积求解较为灵活,可自由选择顶点和底面,从而使问题简捷求解.

3 形化数

代数化是处理立体几何问题的重要方式,代数化在立体几何中最直接的体现就是空间向量的应用,利用空间向量的坐标运算,可轻松实现对空间平行或垂直关系的判断,以及空间角和空间距离问题的求解.

例3 如图4所示,在长方体ABCD-A1B1C1D1中,已知底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.

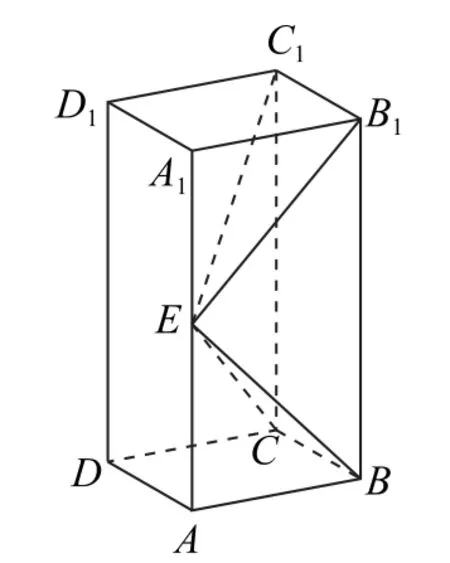
图4

(1)证明:BE⊥平面EB1C1;

(2)若AE＝A1E,求二面角B-EC-C1的正弦值.

(1)在长方体ABCDA1B1C1D1中,B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,所 以B1C1⊥BE.又BE⊥EC1,且B1C1∩EC1＝C1,所以BE⊥平面EB1C1.

(2)由(1)可知BE⊥EB1,结合已知可得Rt△ABE≌Rt△A1B1E,所以∠AEB＝45°,故AE＝AB,AA1＝2AB.以D为坐标原点,建立如图5 所示的空间直角坐标系D-xyz,设CD＝1,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),所以

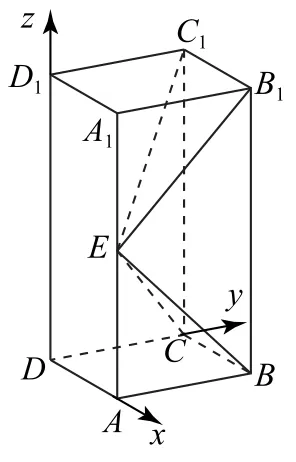
图5

应用向量法解题的基本步骤是先寻找或证明三条线两两互相垂直,进而建立空间坐标系,写出相关点的坐标,求出相应直线的方向向量与平面的法向量,再利用向量的坐标运算解决问题.

4 正化反

在处理立体几何中的判定存在性问题时,我们可假设待判定的结论成立,再逆向探究其成立的结论与已知是否相悖,若相悖,则假设不成立.

例4 如图6所示,在棱长为1的正方体ABCDA1B1C1D1中,若E是棱AA1上的一个动点,则是否存在点E,使得B1D⊥平面BED1?

图6

假设存在点E,使得直线B1D⊥平面BED1,由线面垂直的性质可知B1D垂直于平面BED1内的任意一条直线,因为BD1⊂平面BED1,所以B1D⊥BD1.由正方体的性质可知四边形BDD1B1为矩形,且其对角线B1D,BD1不垂直,这与假设矛盾,故不存在点E,使得B1D⊥平面BED1.

本题中E为动点,平面BED1为动平面,动中寻定,平面BED1中的BD1为定线,先假设待证结论成立,即B1D⊥平面BED1,则B1D⊥BD1,这与已知矛盾.

5 抽象化直观

在平面中某些几何体的直观图并不能很好地反映出几何体的性质和特征,如果能准确把握这些几何体与特殊几何体的关系,将其还原到特殊的几何体(如长方体或正方体)中,则其性质能更直观地体现,从而顺利找到解题的入手点.

例5 已知正三棱锥P-ABC的外接球为球O,△ABC的边长为2,PA,AB的中点分别为E,F,且,则球O的体积为________.

如图7所示,因为E,F分别是PA,AB的中点,所 以EF//PB.因 为,即CE⊥EF,所以CE⊥PB.令AC的中点为D,连接PD,DB.因为PA＝PC,所以AC⊥PD,又AB＝BC,所以AC⊥BD,且PD∩BD＝D,所以AC⊥平面PBD,而PB⊂平面PBD,所以AC⊥PB.又CE⊥PB,所以PB⊥平面PAC,PB⊥PA,PB⊥PC,进而可知PA,PB,PC两两垂直.如图8所示,结合正方体的性质,将正三棱锥P-ABC置于正方体中,则球O也是正方体的外接球,且正方体的对角线为球O的直径.由AB＝2,可得正方体的体对角线为6,所以球O的半径为,球O的体积为

图7

图8

在得出P-ABC为三条侧棱两两垂直的正三棱锥后,不难发现其恰为正方体的一角,故将其还原到正方体中.

(完)