定积分微元法的教学探析与思考
李灵晓 黄元元 王锋叶
摘 要:本着教育数学的思路,结合分析和比较三种微元法观点探析定积分微元法的主要思想,总结出定积分微元法的使用特点及判定方法,并运用微元分析法解决曲边扇形面积和变力对质点的冲量两个问题,该方法类似可推广到其他几何、物理及经济问题.
关键词:高等数学;定积分;微元法;高阶无穷小;教育数学
中图分类号:G642 文献标识码:C
Exploration and Reflection on the
Teaching of Differential Element Method of Definite Integral
Li Lingxiao Huang YuanYuan Wang FengYe
School of Mathematics and Statistics,Henan University of Science and Technology HenanLuoyang 471000
Abstract:According to the idea of educational mathematics,this paper analyzes the main ideas of definite integral differential element method,combined with the analysis and comparison of three viewpoints of differential element method.The application characteristics and judgment methods of definite integral and differential element method are summarized.The differential element analysis method is used to solve the two problems of the sector area of the curved edge and the impulse of the variable force to the mass point.This method is similar and can be extended to other geometric,physical and economic problems.
Keywords:advanced mathematics;difinite integral;differential element method;infinitesimal of higher order;educational Mathematics
1 概述
大學数学教育的任务,就是运用教育数学的思路,将已有的数学成果进行再创造,适当地改进数学表述形式,使之更加科学、更加适合于教学[1]。高等数学教材就有很多这样的概念,既经典又凝练,如何优化其概念表述方式让它更适合学生接受?这也是我们数学教育工作者值得思考的一个问题。文献[2]对于数学知识的结构和表现方法提出以下三条标准:(1)逻辑结构尽可能简单;(2)概念引入要平易直观;(3)要建立有力而通用的解题工具.这也是教育教学追求的主要目标.
在解决几何、物理、经济等领域中的一类实际问题时,往往用定积分来解决,而微元法(或“元素法”)正是解决该类问题过程中最常用及最方便的方法。什么是微元法?不同的教材有不同的表述方法,而不同的教师又有不同的理解,但大多表达较为隐晦而凝练,学生接受起来有一定的难度.本文首先结合分析三种微元法观点来讨论微元法的主要思想(可参阅文献[39],尤其是文献[5]),其次给出微元法的使用特点、判定方法,最后给出两个相关几何和物理应用.
2 有关微元法的不同表述
2.1 概念定义法
微元法实质上就是定积分定义中的三步法——分割、近似求和、取极限的简化,其理论基础是定积分的定义及被积函数的可积性.这种说法虽然理论上无懈可击,但在叙述及方法的运用上过于烦琐、零碎,而且对一些物理量(如质量、转动惯量、引力)的大小用定义给出的方法有点儿勉强,因为这些量都是客观存在的,它们量值的大小是不以人的主观定义而改变的.因而这种说法的合理性还须保证相应的定义的合理性.
2.2 物理直观法
这种方法采用牛顿、莱布尼茨当时创立微积分时对定积分是所谓对无穷小量(微元)的加法的思想.具体地讲,就是要计算一个实际量I,先将这个量分成部分量的和I=∑ΔI,再通过寻找函数f(x),求得部分量的一个线性(关于Δx的)近似表达式ΔI≈f(x)Δx,这里一般要求f(x)连续,f(x)Δx就是实际量I的一个(积分)微元(元素).从而I=∑ΔI≈∑f(x)Δx,这里∑表示对离散量求和,将其换为对连续量求和即定积分就得到了实际量I的计算公式I=∫baf(x)dx.这种方法直观、简洁、有效,被现在大多数的物理学家或物理教师所采用,但其并不具有数学的严格性,因为它并没有说清楚为什么把∑换为∫,就把一个原本是近似的等式变成了精确等式,这种缺陷也是微积分初创时期备受指责的原因之一.虽然在物理上可以通过数据去验证等式,从而弥补此缺陷,但这不能兼容于数学家(数学家和物理学家往往在严谨性方面理解不同,数学家认为,一百个实际验证也不会比一个理论证明更可信;而物理学家则觉得一百个理论证明也比不上一个实际验证更可靠).
2.3 微分推导法
这种方法吸收以上两种方法优点,既有物理的直观,又有数学的严谨.具体说来就是:要计算一个实际量I,这个量必须具有两个特性:(1)I是一个与某变量x的变化区间[a,b]有关的量,即量I是一个分布在区间[a,b]上的整体量;(2)I对于[a,b]具有可加性,即I=∑ΔI.在(1)、(2)基础上,为了求实际量I,需建立一个关于I的函数I(x)(常称之为分布函数),使得I(a)=0,I(b)=I,且I=∑ΔI,其中應该注意:ΔI既是I在[a,b]的子区间[x,x+dx]上所对应的部分量,又是函数I(x)在子区间[x,x+dx]上的改变量,即ΔI=I(x+dx)-I(x).如果能找到f(x),使得ΔI的近似表示式是ΔI≈f(x)Δx,并且ΔI=f(x)Δx+o(Δx),这里o(Δx)表示Δx的高阶无穷小(Δx→0),从而函数I(x)可微,且I′(x)=f(x)或dI=f(x)dx(微元或微分表达式),而f(x)(常称之为I(x)的密度函数或边际函数)一般要求为连续函数,从而就可推得I=∫baf(x)dx.
3 微元法三种表述的关系及框图说明
在上述微元法的三种表述中,我们着重分析了它们的区别,当然我们也可从联系和共性的方面来对之进行分析.下面用三行框图来分别表示上述的概念定义法、物理直观法及微分推导法,从中也反映了三者间的一些联系.
因为概念定义法分割区间、取i都要求有任意性,求和、求极限又是固定模式,故可简述其过程,从而就化为物理直观法:
在微段[x,x+Δx]上,I累积的微量ΔI,代之以微分dI=f(x)dx,(dx=Δx),就可简化成微分推导法,当然,关系式ΔI=f(x)Δx+o(Δx)一般不作验证.
上面三种方法尤其第三种“微元推导法”,其核心可压缩为以下框图:
用以上所表示的形式,来解决求实际量I的方法,称为微元法.在对实际量I建立定积分的微元法中,dI称之为I的积分微元或积分元素.若量I表示面积,dI就称为面积微元;若量I表示体积,dI就称为体积微元;若量I表示质量,dI就称为质量微元;等等.应该注意,作为实际量的I,它是一个常数值,如曲边梯形的面积、旋转体的体积、细棒的质量等,但微元dI中的I实质上是实际量I的分布函数,换句话说,这里的符号I也是身兼两职.
微元法在解决实际问题时具有简单、直观、方便的特点,且应用广泛,应熟练掌握之.
4 微元法的使用特点
微元法的使用特点即能用定积分计算的量I所须满足的条件,有下列三条:
①I与某变量x的变化区间[a,b](区间有时也可以是无穷的)有关;
②I对于区间[a,b]具有可加性;
③I的部分量ΔI可近似地表示成f(x)·Δx,或者说求得微分表达式dI=f(x)dx.
从上面三个条件可以看出,微元法的关键是求微分表达式或者说微元表达式dI=f(x)dx(这也是我们将这种方法称为微元法的主要原因),而微元表达式成立的前提是验证一个高阶无穷小:ΔI=f(x)Δx+o(Δx),即证明
limΔx→0ΔI-f(x)ΔxΔx=0(*)
而事实上,要验证(*)式成立在实际问题中不是一件容易事情,有时验证(*),其难度甚而超过了找f(x)以及求定积分本身.也正因为此,为了在微元法中不至于“喧宾夺主”,这一条件的验证往往被略去或者被淡化,这也许是微元法不叫“微分法”的一个缘由吧,当然这同时也是微元法受到质疑的原因.
5 微元法中高阶无穷小成立的判定方法
如何做到既要保证(*)式成立(严谨的需要),又不需要直接验证它(方便的需要)?文献[10]通过一个求曲边梯形面积的问题,总结出一个命题,我们将其改造并推广为更易于接受的一种数学表述形式,得到以下两个判定定理.
定理1(判定法则1)设I是分布在区间[a,b]上的一个量,I(x)为区间[a,b]上的分布函数,且I(a)=0,I(b)=I,ΔI为I在[x,x+Δx][a,b]上的部分量,也是I(x)在小区间上的函数增量,即ΔI=I(x+Δx)-I(x),若存在一个连续函数f(x),使得Δx·mxf(x)≤ΔI≤Δx·Mxf(x),其中Δx>0,mxf(x),Mxf(x)分别是f(x)在[x,x+Δx]上的最小值和最大值,则limΔx→0ΔI-f(x)ΔxΔx=0,即dI=f(x)dx,且I=∫baf(x)dx.
证明:∵f(x)在[x,x+Δx][a,b]上连续,
∴mxf(x),Mxf(x)在[x,x+Δx]上是存在的。
由已知条件Δxmxf(x)≤ΔI≤ΔxMxf(x)
从而mxf(x)-f(x)≤ΔI-f(x)ΔxΔx≤Mxf(x)-f(x)
再由f(x)在[x,x+Δx][a,b]上连续,
∴当Δx→0时,mxf(x)-f(x)→0,Mxf(x)-f(x)→0
∵由夹逼定理知limΔx→0ΔI-f(x)ΔxΔx=0,即ΔI-f(x)Δx=o(Δx),从而dI=f(x)dx,且I=∫baf(x)dx.证毕.
上面我们讨论的是所求量为标量的情况,进一步,我们可将其推广到矢量的情况.
设向量A→=A1,A2,A3为所求的实际量,定义A→(x)为相应一元向量分布函数,ΔA→为A→(x)关于自变量x的子区间[x,x+Δx]上的改变量,ΔA→=ΔA1,ΔA2,ΔA3,其中ΔA1,ΔA2,ΔA3为ΔA→分别在x轴、y轴及z轴上的标量.
定理2(判定法则2)对ΔAi,若fi(x)为连续函数且满足:
Δx·mxfi
Δx·Mxfi,(i=1,2,3)
则A→=∫Rf→(x)dx,其中f→=f1(x),f2(x),f3(x),mxfi,Mxfi分别为fi在小区间上的最小、最大值.
证明:∵fi(x)为连续函数
∴fi(x)在相应坐标轴上的子区间上都存在最大值Mif和最小值mif
又∵Δxmxfi
ΔxMxfi,
∴由判定法则1可同理得到Ai=∫Rfi(x)dx,(i=1,2,3)
∴A→=A1,A2,A3=∫Rf1(x)dx,∫Rf2(x)dx,∫Rf3(x)dx=∫Rf→(x)dx
到此,我们可以看出,只要所求量满足判定法则1或2的条件,由定理就可判定可以用微元法将所求实际量化为定积分来计算.
6 用微元法计算实际量I的步骤
设所求实际量I满足微元法的使用特点,则可按下列步骤将I化作定积分:
(1)根据所求问题,选取一个变量x为积分变量,并确定它的变化区间[a,b],建立实际量的分布函数I(x),使得I(a)=0,I(b)=I;
(2)設想将区间[a,b]分成若干小区间,取其中的任一小区间[x,x+Δx],找出[a,b]上的非负连续函数f(x),使得在[x,x+Δx]上,部分量ΔI有近似关系ΔI≈f(x)dx;
(3)在子区间[x,x+Δx]上,验证条件Δx·mxf(x)≤ΔI≤Δx·Mxf(x),从而可得微元表达式dI=f(x)dx;
(4)以[a,b]为积分区间,计算定积分I=∫baf(x)dx.
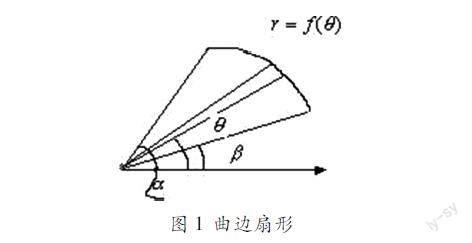
7 微元分析法在几何中的应用——曲边扇形面积
例1:设由曲线r=f(θ)及射线θ=α,θ=β围成一图形(简称曲边扇形,右图1),这里f(θ)在[α,β]上连续,且f(θ)≥0,求曲边扇形的面积I.
图1 曲边扇形
解设I(θ)是由射线θ=α和角度为0的射线及f(τ)(τ∈[α,θ])围成的图形的面积.
任取θ∈[α,β],并取Δθ∈[0,β-α],使θ+Δθ∈[α,β],则在[θ,θ+Δθ]上的曲边扇形是以角度为θ,θ+Δθ的射线及曲线r=f(τ)(τ∈[α,θ])所围成的平面图形,其面积为ΔI,又因f(θ)在[α,β]上连续,所以分别存在最大值及最小值maxτ∈[θ,θ+Δθ]f(τ),minτ∈[θ,θ+Δθ]f(τ).
∵ΔI≥Δθ2ππminτ∈[θ,θ+Δθ] f2(τ)=12minτ∈[θ,θ+Δθ] f2(τ)Δθ
ΔI≤Δθ2ππmaxτ∈[θ,θ+Δθ] f2(τ)=12maxτ∈[θ,θ+Δθ] f2(τ)Δθ
即 12minτ∈[θ,θ+Δθ] f2(τ)Δθ≤ΔI≤12maxτ∈[θ,θ+Δθ] f2(τ)Δθ
∴由判定法则1得:I=∫βα12 f2(θ)dθ.
8 微元分析法在物理中的应用——变力对质点的冲量[11]
例2:一个质量为m的质点在坐标oxy平面上运动,其在某一时刻t的位置矢量为r→=(acosωt,bsinωt).求质点A到质点B的冲量I及外力做功W.
解在任一时刻t时,质点速度:v→=dr→dt=(-ωasinωt,ωbcosωt),而其加速度为a→=dv→dt=-(ω2acosωt,ω2bsinωt).
由牛顿第二定律,该质点在任一刻t受到的力为:
F→=ma→=(F1,F2)=-(mω2acosωt,mω2bsinωt).
在运动过程中小球在[t,t+Δt]上的冲量改变量为:ΔI=(ΔI1,ΔI2),则不难得到:
-mω2acosωtdt
-mω2bsinωtdt
故由判定法则2得:
I→=∫π2ω0F→dt=∫π2ω0(-mω2acosωt,-mω2bsinωt)dt=-mω(a,b).
下再求外力做功,利用W=F→·S→=F→·v→t,并设在[t,t+dt]内功函数改变量为ΔW,则:
m(-ω2acosω(t+Δt),-ω2bsinω(t+Δt))·(-ωasinω(t+Δt),ωbcosω(t+Δt)dt
m(-ω2acosωt,-ω2bsinωt)·(-ωasinωt,ωbcosωt)dt
从而再由判定法则1得:
W=∫π2ω0F→·v→dt
=∫π2ω0(-mω2acosωt,-mω2bsinωt)·
(-ωasinωt,ωbcosωt)dt
=∫π2ω0(mω3a2sinωt-mω3a2sinωtcosωtdt
=mω22(a2-b2)
9 结论
定积分微元法是处理几何、物理及經济应用问题的一个理论基础,以教育数学思路为导向,就曲边扇形的面积和变力对质点的冲量运用判定法则1和2分别进行了分析和计算,类似可考虑弧长、旋转体体积、细棒质量、变力做功、转动惯量及经济问题。定积分微元分析法可以推广为多元函数情形,对于重积分、线面积分的几何、物理、经济应用问题的分析与解决也是一个极好的借鉴。
致谢:非常感谢郑州大学李梦如教授提供的相关参考文献[1][2]和[5]对本文的启发以及审稿专家提出的宝贵意见。
参考文献:
[1]韩云瑞,刘庆华.从教育数学看高等数学教材[J].高等数学研究,2005,8(2):3336.
[2]张景中.从数学难学谈起[J].世界科技研究与发展,1996(2):2029.
[3]马知恩,王绵森.工科数学分析[M].高等教育出版社,2001.
[4]闫站立.微积分(第二版)[M].高等教育出版社,2007.
[5]韩云瑞.微积分概念解析[M].高等教育出版社,2007.
[6]同济大学数学系.高等数学[M].高等教育出版社,2007.
[7]吴赣昌.高等数学(理工类)[M].中国人民大学出版社,2007.
[8]大学数学编写委员会.高等数学[M].科学出版社,2017.
[9]张天德,王玮.高等数学[M].人民邮电出版社,2020.
[10]贺秋林.微元法原理探究[J].工科数学,2001,17(3):9596.
[11]黄生训,杨红.微元法在普通物理力学中的应用[J].中国科技信息,2006(08):301302.
基金项目:国家自然科学基金(12101193);河南省高等教育教学改革研究与实践立项项目(2021SJGLX381);2023年高等学校大学数学教学研究与发展中心项目“基于信息技术和学科交叉的高等数学课程教学创新与实践”(项目编号:CMC20230205);智慧教学背景下高等数学课程创新型数学体系的构建与优化设计研究(2023)
作者简介:李灵晓(1976— ),女,硕士,教授,从事高等数学教学和非线性数学物理的研究。

