Value Iteration-Based Cooperative Adaptive Optimal Control for Multi-Player Differential Games With Incomplete Information

Yun Zhang , Lulu Zhang , and Yunze Cai

Abstract—This paper presents a novel cooperative value iteration (VI)-based adaptive dynamic programming method for multi-player differential game models with a convergence proof.The players are divided into two groups in the learning process and adapt their policies sequentially.Our method removes the dependence of admissible initial policies, which is one of the main drawbacks of the PI-based frameworks.Furthermore, this algorithm enables the players to adapt their control policies without full knowledge of others’ system parameters or control laws.The efficacy of our method is illustrated by three examples.

I.INTRODUCTION

TODAY, in areas such as intelligent transportation and military, many complex tasks or functions need to be implemented through the cooperation of multiple agents or controllers.In general, these agents are individualized and have their own different incentives.This individualization forms a multi-player differential game (MPDG) model.In such game models, players are described by ordinary differential equations (ODE) and equipped with different objective functions.Each player needs to interact and cooperate with others to reach a global goal.Dynamic programming (DP) is a basis tool to solve an MPDG problem, but solving the so-called coupled Hamilton-Jacobi-Bellman (CHJB) equations and the“curse of dimensionality” are the main obstacles to the solution.

To overcome above difficulties, a powerful mechanism called adaptive DP (ADP) [1] was proposed.ADP approximates optimal value functions and corresponding optimal control laws with nonlinear approximators and has been applied successfully in problems of nonlinear optimal control [2], trajectory tracking [3] and resource allocation [4].A wide range of ADP frameworks have been developed so far to deal with different MPDG formulations [5]-[9].Most of state-of-the-art developments are based on policy iteration (PI) for policy learning [6], [10], [11].A common feature of these PI-based methods is that it requires a stabilizing control policy to start the learning process [12].However, this is an overly restrictive assumption, especially when the system is complicated and strongly nonlinear.To relax the above assumption, value iteration (VI) is an important alternative approach which does not need to assume the initial policy is stabilizing.Recently,some variant VI methods have been developed in discretetime linear and nonlinear systems and the convergence proofs of these methods have been considered [13], [14].However, a continuous-time counterpart of the VI method is missing for continuous-time MPDG problem with continuous state and action spaces.It is worth mentioning that in [12], authors propose a VI-based algorithm to obtain the optimal control law for continuous-time nonlinear systems.This result can be a basis for a VI-based ADP framework for MPDG.

MPDG equipped with incomplete information structure has always been one of the most popular study topics.With incomplete information structure, players do not have complete information of others, such as states and policies.This setting is of practical value because factors like environmental noise or communication limitation may make the complete information assumption fail.No matter what causes the imperfection, it is advantageous for agents to search for optimal policies with less requirement of information.There exist many frameworks proposed to deal with partially or completely unknown information about teammates or opponents in MPDG, where the missing information can be model dynamics or control polices.For unknown dynamics, [15] and[16] introduce a model identifier to reconstruct the unknown system first.Another common way is to remove dynamics parameters from CHJB with the help of PI framework, see [8],[17], [18].However, to compensate for the lack of model information, most studies above require knowledge of the weights of the other players.A few researches attempt to circumvent this limitation.Some studies try to estimate the neighbors’ inputs by limited information available to each player [19], [20].In [21], authors use Q-learning to solve discrete-time cooperative games without knowledge of the dynamics and objective functions of the other players.

The objective of this article is to provide a VI-based ADP framework for continuous-time MPDG with incomplete information structure.The information structure we are interested in is the one where players do not have knowledge of the others’ dynamics, objective functions or control laws.Firstly, we extend the finite horizon HJB equation in [12] to the best response HJB equation for MPDG.It shows that with the policies of all other players fixed, MPDG problem can be considered as an optimal control problem for a single-controller system.Secondly, we divide players into two categories for learning process.In each learning iteration, only one player adapts its control law and all others do not.With the above design, we give our cooperative VI-based ADP (cVIADP)algorithm.This new algorithm does not need initial admissible policy any more, and it can update control polices by solving an ODE instead of coupled HJB equations.Furthermore,in the learning process of each player, the state of the system and parameters of its own objective function and control law are the only information needed.

The structure of this article is organized as follows: Section II formulates the MPDG problem and introduces necessary preliminaries about DP and HJB equations.In Section III, our VI-based ADP framework for MPDG is proposed and its convergence is proven.An NN-based implementation of our cVIADP framework is given in Section IV and we prove the estimated weights converge to the optimal solutions.The performance of our algorithm is demonstrated in Section V by two numerical simulations.Finally, the conclusions are drawn in Section VI.

II.PROBLEM FORMULATION AND PRELIMINARIES

A. Problem Formulation

Consider the dynamic system consisting ofNplayers described by

dent onu-i, when integrating,u-iaffects the trajectory ofx,and affects the valueJiindirectly.

The classical Nash equilibrium solution to a multi-player game is defined as anN-tuple policywhich satisfy

An undesirable situation may occur with such definition when each player has no influence on each other’s costs.In this case, every player chooses its own single-controller optimal solution since for any different policies of all other playersu-i,i,

To rule out such undesirable case, we use the following stronger definition of Nash equilibrium.

Definition 1(Interactive Nash Equilibrium[22]): AnNtuple policy,...,} is said to constitute an interactive Nash equilibrium solution for anN-player game if, for alli∈[1:N], condition (3) holds and in addition there exists a policyfor player k (k≠i) such that

The basic MPDG problem is formulated as follows.

Problem 1: ∀i∈[1:N],∀x0∈Ω, Find the optimal strategyfor playeriunder the dynamics (1) such that theNtupleconstitutes an interactive Nash equilibrium.

Problem 1 is assumed that complete information is available to all players.To elaborate the setting of incomplete information, we define an information set of playeriover a time interval [t0,t1] as

wherex([t0,t1]) represents the state trajectory of all players over a time interval [t0,t1].The MPDG problem with incomplete information is given as below.

Problem 2: Solve Problem 1 under the assumption that playerihas only access to Fi([t0,t1]) over a time interval[t0,t1].

Remark 1: The incomplete information structure is characterized by the limit information from neighbors.Note that all elements exceptxin Fi([t0,t1]) are equipped with subscripti,which means objective functions and control policies of neighbors are unavailable for playeri.The statexis the only global information accessible to all players, and the players can only depend on Fi([t0,t1]) to obtain their own optimal polices.

B. Dynamic Programming for Single-Controller System

IfN=1, Problem 1 is equivalent to an optimal control problem of a single-controller system.One can solve this problem by dynamic programming (DP) theory.Consider the following finite-horizon HJB equation:

whereV(x,s):Rn×R →R.

The following lemma ensures the convergence ofV(x,s),and its proof can be found in [12].

III.VALUE ITERATION-BASED ADP FOR MULTI-PLAYER GAMES

In this section, we design a VI framework to obtain optimal policy for each player aimed at Problem 1, and give the convergence proof of this framework.Thus, throughout this section, we assume all players have complete information of the game model temporarily.

Define the best response HJB function for playerias (7)with arbitrary policies µ-i,

withVi(·,0)=V0(·).

Assumption 1:V0(·)∈P is proper and (10) admits a unique solution.

First we introduce the following lemma, which can be considered as an extension of Lemma 1 for multi-player systems.

We borrow the concepts ofadaptingplayers andnon-adaptingplayers in [21].As defined therein, the adapting player is the one who is currently exciting the system and adapting its control law while non-adapting players keep their policies unchanged.

3)Role Switching: Select another playeri+1 as the adapting player, and the playeriis set to be non-adapting.

Remark 2: In Step 3, all players are pre-ordered as a loop.After the adaptation of playerNends, player 1 is selected as a new circulation.

Remark 3: The cooperation among players shows up in two ways.On the one hand, players need to communicate with each other to obtain necessary information for iterations.On the other hand, as stated in Remark 2, players need to negotiate to determine an order.

The following theorem shows the convergence of the cooperative VI.

Proof: Lets→∞ in (11), and with (12), one has

From (12) again, it has

Therefore,

According to (16) and (17), it follows that:

and by integration we have

IV.NN-BASED IMPLEMENTATION OF COOPERATIVE VI-BASED ADP WITH INCOMPLETE INFORMATION

The VI framework introduced in Section III depends on complete information ofTo circumvent this assumption and solve Problem 2, an NN-based implementation of cooperative VI is given in this section.

Remark 5:The choice of the basis function family varies from case to case.Polynomial terms, sigmoid and tanh function are commonly used.Polynomial basis can approximate functions in P more easily and with appropriate choice, the approximation scope can be global.Sigmoid or tanh functions are more common in neural network and have good performance in local approximation.

The corresponding estimation of µiis given by

Remark 7: The role of Line 7 in Algorithm 1 is to excite the adapting player and satisfy the Assumption 2.At the same time, since the convergence of the best response HJB equation in Lemma 2 is based on fixed policy µ-i, the probing noise is only added to the adapting player and the other players follow their own policies without noise.

Proof: The proof consists of two steps.Step one, show that the the solutionconverges asymptotically to.Since the policies of all other players are fixed, (25) is the best response HJB equation (10) for playeri.Let

In this section, we present several examples to verify the performance of the proposed VI algorithm in Section IV.

A. Example 1: A 2-Player Nonlinear Game

First, we consider a 2-player nonlinear game where the input gain matricesgi(x),i=1,2 are constant.The system model is described by

Fig.1 shows the evolutions of]converge after 33 iterations for each controller.The estimated value surfaces ofare depicted in Fig.2, which verify that∈P.Fig.3 shows the system trajectory with the same initial state under initial and learned control laws.The policy obtained by our cVIADP makes the system converge to the equilibrium point more quickly and eliminate the static error of initial policy.

Remark 9:Notice that in Fig.2, the value ofVˆ[k]increases

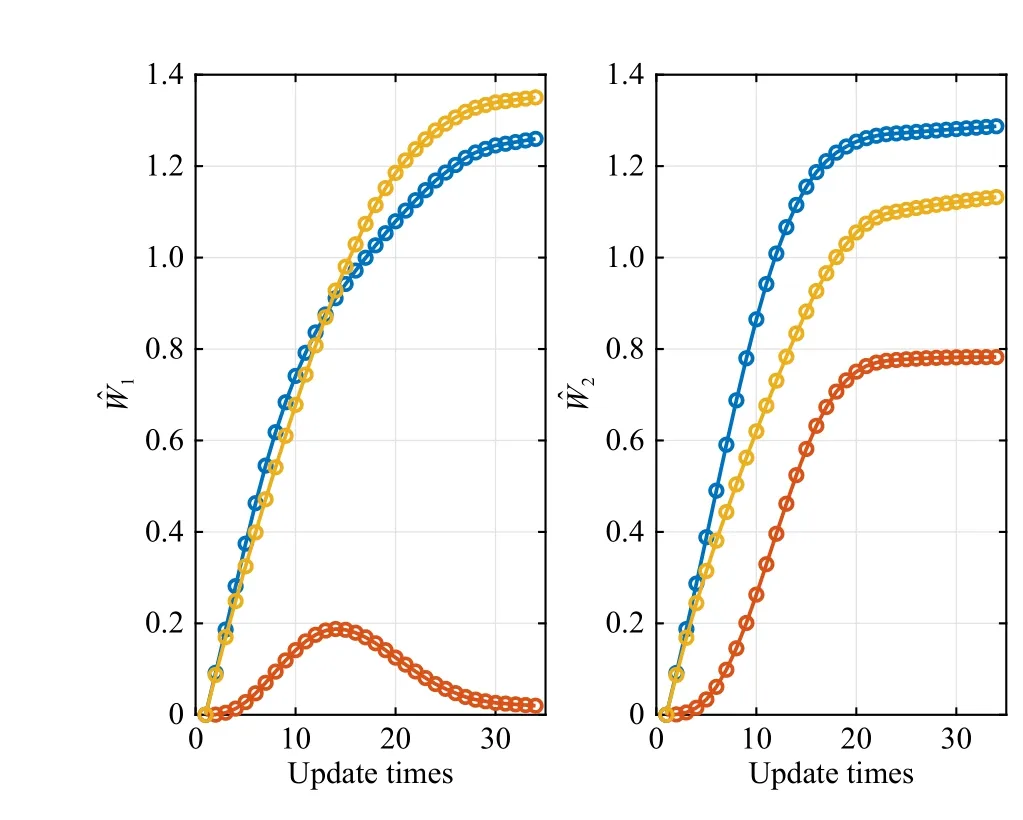
Fig.1.Updates of weights of two controllers in Example 1.

Fig.2.Value surfaces of estimated functions Vˆ[k] for different k in Example 1.

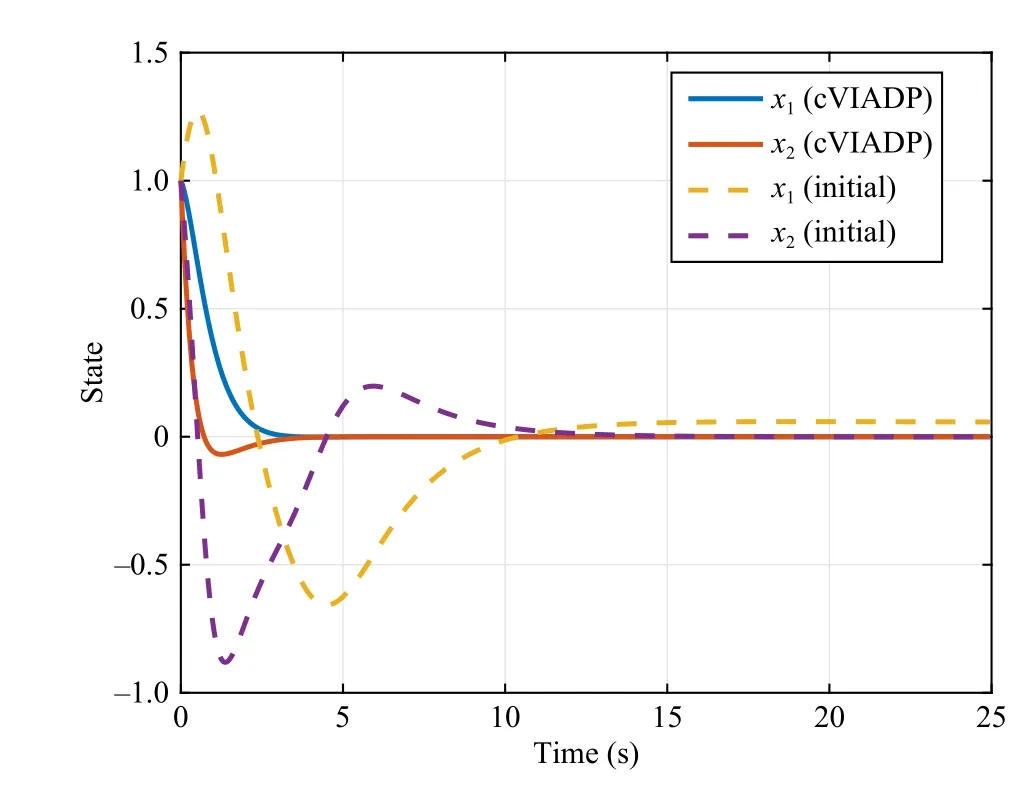
Fig.3.Evolutions of system states with learned policy (solid) and initial policy (dashed) in Example 1.

B. Example 2: A 3-Player Nonlinear Game

dependentgi(x).The dynamics is described as follows [15]:

Next, we consider a 3-player nonlinear game with state-

Fig.4 shows the evolutions ofThe algorithm converges after 15 iterations for each player.The iterations ofare depicted in Fig.5.To test the performance of the learned policy, both the policies after and before the learning process are applied to the system with the same initial conditions.Fig.6 shows the evolution of the system state.Notice that the system with the initial policy is unstable.However after learning, the policy can stabilize the system.This experiment shows that our cVIADP algorithm can work without the dependence of initial admissible policy, which is the main limit of PI-based algorithms.

Fig.4.Updates of weights of three controllers in Example 2.

C. Example 3: A Three-Agent Linear Game

Finally, we consider a non-zero-sum game consisting of three agents with linear independent systemsx˙i=Aixi+Biui,i=1, 2, 3, given by

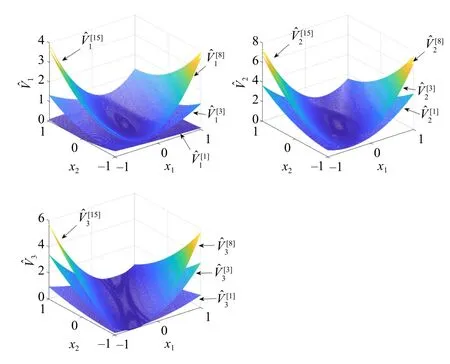
Fig.5.Value surfaces of estimated functions Vˆ[k] for different k in Example 2.

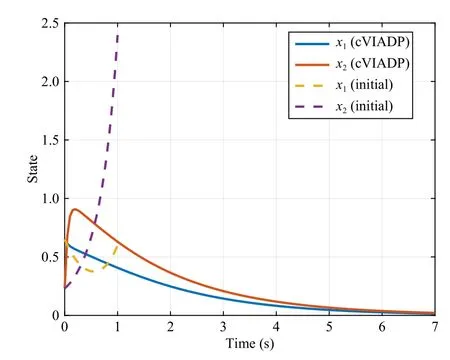
Fig.6.Evolution of system states with learned policy (solid) and initial policy (dashed) in Example 2.

Letx=[x1,x2,x3]T, and (32) can be integrated into the same form as (1) withf=diag{A1,A2,A3}1d iag{A1,A2,A3} is a block matrix whose diagonal elements are A 1,A2,A3 and zero otherwise.,g1=[BT1, 01×2,01×2]T,g2=[01×2,BT2, 01×2]Tandg3=[01×2, 01×2,]T.

The parameters of objective functions areQ1=I2,Q2=2I2,Q3=0.5I3,R1=2R2=R3=1.The basis function family is chosen as {ϕi(x)}=∪1≤p≤q≤3{xq} and the corresponding partial derivative { ∂xϕi(x)} is calculated.

The value surfaces of the estimated value functionsVˆiwith respect toxiare plotted in Fig.7.In each sub-figure, the statex-iis fixed asx-i(0).As we can see from Fig.8, the ADP algorithm converges after 7 iterations for each player.Fig.9 shows the state evolutions of three agents, indicating the learned policies stabilize all agents.

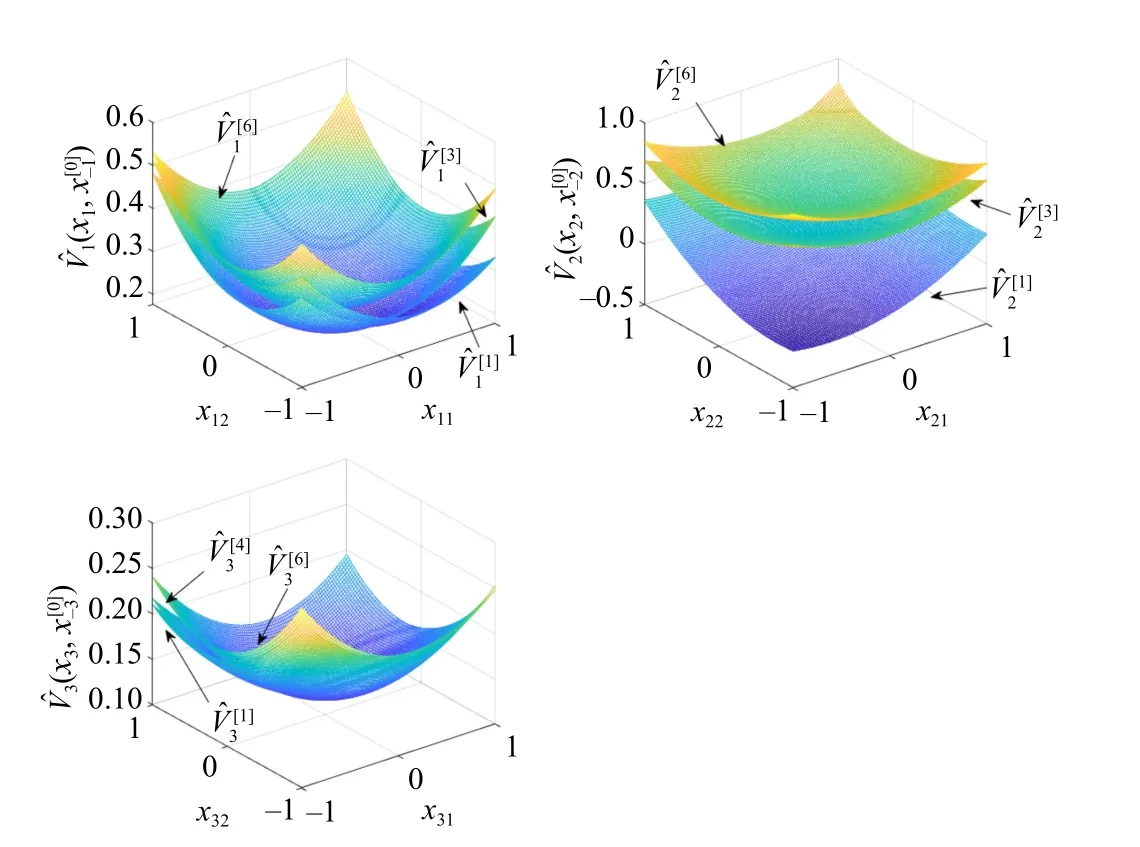
Fig.7.Value surfaces of estimated function Vˆi in Example 3.In each subfigure, the state x-i is fixed at x-i(0) and the surfaces illustrate the graph ofVˆi w.r.t xi.

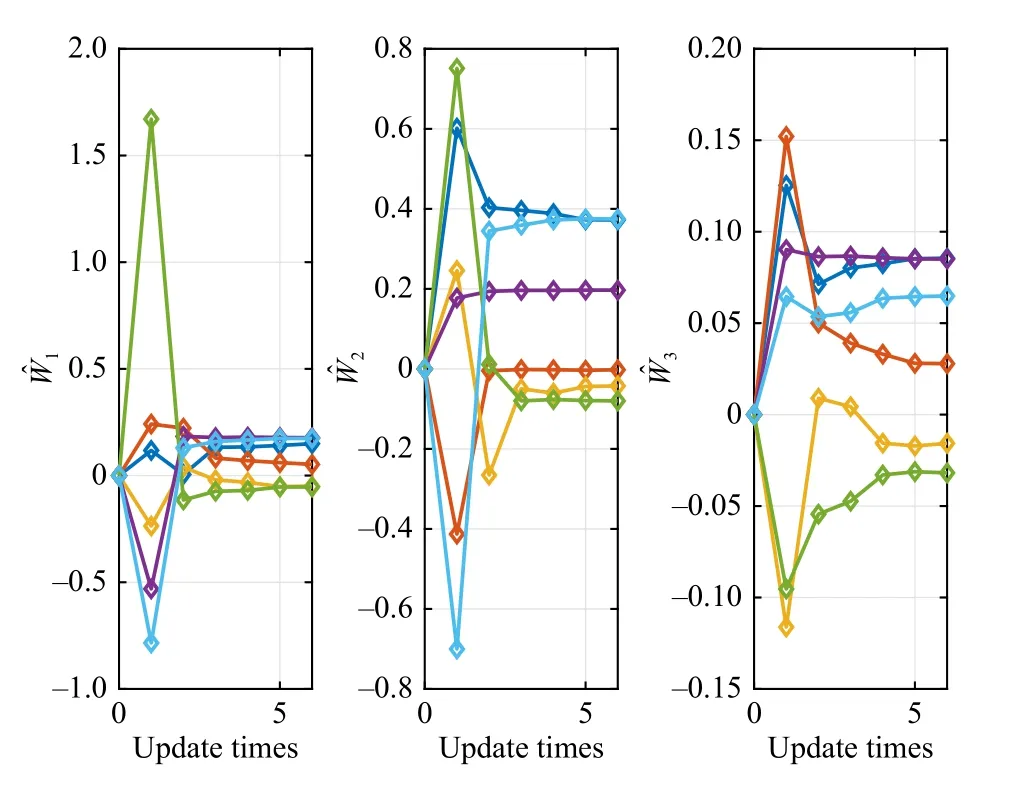
Fig.8.Updates of weights of three agents in Example 3.

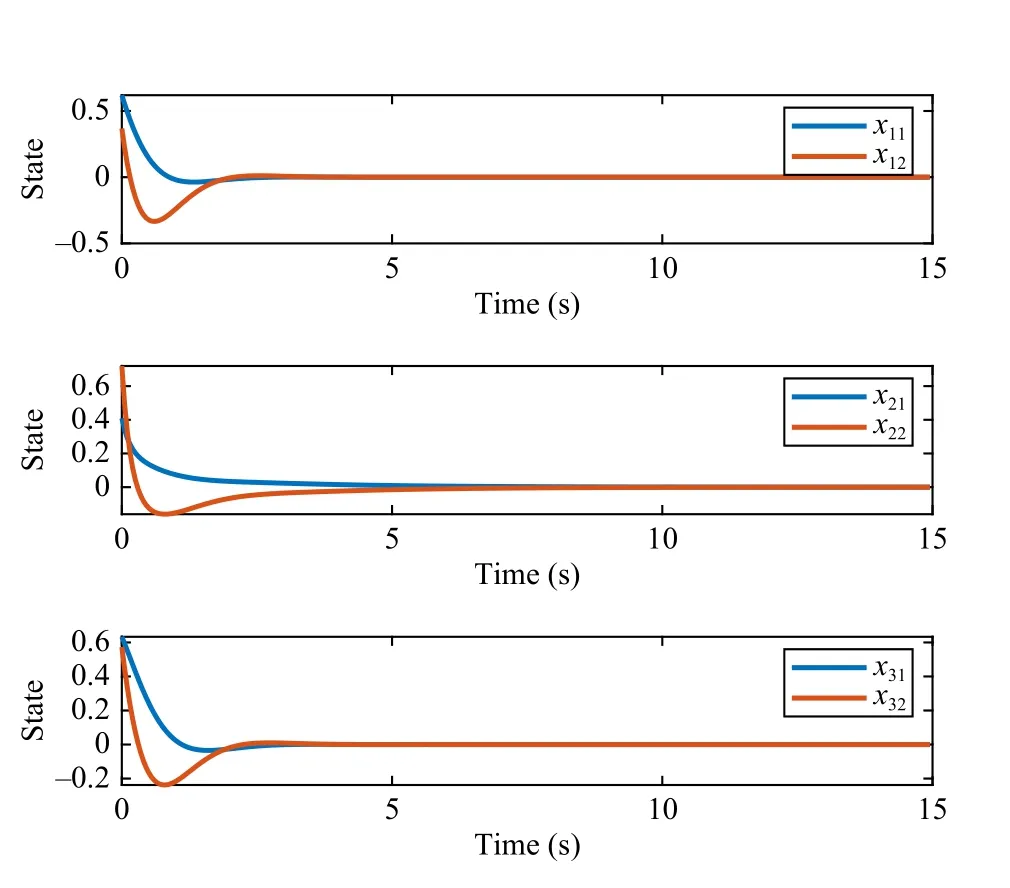
Fig.9.State evolutions of three agents in Example 3.

VI.CONCLUSION

In this paper, we propose a cooperative VI-based ADP algorithm for continuous-time MPDG problem.In cVIADP, players learn their optimal control policies in order without knowing parameters of other players.The value functions and control policies of players are estimated by NN approximators,and their policy weights are updated via an ordinary differential equation.Furthermore, the requirement of stabilizing initial control policies of PI-based algorithm is removed.In future work, we will focus on practical implementation aspects such as role switching mechanism and efficient excitation.