Decentralized Optimal Control and Stabilization of Interconnected Systems With Asymmetric Information

Na Wang , Xiao Liang , Hongdan Li , and Xiao Lu

Abstract—The paper addresses the decentralized optimal control and stabilization problems for interconnected systems subject to asymmetric information.Compared with previous work, a closed-loop optimal solution to the control problem and sufficient and necessary conditions for the stabilization problem of the interconnected systems are given for the first time.The main challenge lies in three aspects: Firstly, the asymmetric information results in coupling between control and estimation and failure of the separation principle.Secondly, two extra unknown variables are generated by asymmetric information (different information filtration) when solving forward-backward stochastic difference equations.Thirdly, the existence of additive noise makes the study of mean-square boundedness an obstacle.The adopted technique is proving and assuming the linear form of controllers and establishing the equivalence between the two systems with and without additive noise.A dual-motor parallel drive system is presented to demonstrate the validity of the proposed algorithm.

I.INTRODUCTION

INTERCONNECTED systems have been found widely in a considerable quantity of fields and practical application scenarios, such as smart grids, formation flight, sensor network and cyber-physical systems [1]-[4], which consist of numerical subsystems.To realize a common goal, subsystems exchange and share partial information through the network to make an individual decision where communication delay occurs inevitably due to the limited bandwidth and cache capacity of nodes.Owing to the information available to each subsystem being incomplete and different, decentralized control with asymmetric information has proven to be an effective control scheme to achieve a desirable performance of the system.

The decentralized control with asymmetric information is a kind of control scheme where the decision-maker of each subsystem or station accesses different information to make a decision, which could be traced back to team decision problem [5] and was further studied by Radner [6].The decentralized optimal control problem with asymmetric information is challenging since the optimal control law may be nonlinear[7], [8].Paramount attention has been paid to decentralized control problem over the past decades [9]-[16].Just to name a few, [12] provided a dynamic program for the decentralized control problem with local and remote controllers employing the approach of common information.In [13], decentralized optimal control for a networked control system with asymmetric observations was studied with the assumption of linear controllers.The stabilizing solution was derived under decentralized controllers for the multiplicative-noise stochastic systems in [14].Nevertheless, the results derived in the aforementioned literature mainly pertain to the decentralized control subject to special asymmetric information structure, e.g.,F1⊆F2, where F1,F2denote the information sets available to two controllers of the system respectively, while the more general asymmetric information structure, i.e., F1≠F2and F1⊈F2has not been investigated.Information structure may determine the complexity and tractability of the decentralized optimal control problem in essence, hence playing a decisive role, as mentioned in [7],[8].The decentralized control with a more general information structure where the relationship between the two information sets available to two controllers does not belong to inclusion has attracted lots of research and topics [17]-[22].In particular, with a periodic sharing information pattern, [19]addressed the optimal control problem and proved that the periodic sharing pattern has a non-classical separation property.In [20], one step delayed control sharing was studied applying the dynamic programming method.In [21], the distributed LQG problem with the varying communication delay case was dealt with based on the information hierarchy graph.In [22], optimal control law was derived for a class of lower block triangular systems.Great progress has been made, however, most works mentioned above are involved in the finitehorizon optimal control problem and few efforts have been devoted to the infinite-horizon stabilization problem even though it is a fundamental problem.

Given the discussion above, the decentralized control problem subject to asymmetric information has not been fully explored, which makes further study necessary.We are inspired by the previous work [23] where the optimal control policy was derived using a decomposition method of system state and control input based on noise history with the control weighting matrix positive definite.It is noted that the optimal controllers proposed in [23] are dependent on the noise history, which is essentially an open-loop control and hard to realize from the perspective of implementation due to the unmeasurable additive noises.Furthermore, the infinite-horizon stabilization problem was not taken into consideration either.

To get a closed-loop optimal solution as well as a complete stabilization solution, an interconnected system subject to asymmetric information is considered in this paper, where the state information of a subsystem is transmitted to another subsystem with one step communication delay to make the control policy, whereas the control input does not share.This kind of model derives from production cases, the economic dispatch of the power system for example.The whole power demand is distributed among the generating units, where each unit (subsystem) has some local information on its own environment and shares information through the network with time delay to minimize the total operating cost.Compared with [23], for the finite-horizon case, the solution to the forward-backward stochastic difference equations (FBSDEs) is presented by applying the stochastic maximum principle.Based on the solution, we obtain closed-loop optimal controllers and performance in terms of the solution to the Riccati equation under the assumption that the control weighting matrix is positive semidefinite.In addition, for the infinitehorizon case, we show the system is mean-square bounded if and only if the algebraic Riccati equation admits a unique positive definite solution.

In this paper, the problems of decentralized optimal control and stabilization for interconnected systems involving asymmetric information are investigated.The main challenge lies in threefold: The first is the coupling between control and estimation resulting from asymmetric information structure,which makes the classical separation principle no longer applicable.The second refers to finding the solution to the FBSDEs.Specifically, the information available to two controllers is partial because of one step communication delay,and the different information filtration (asymmetric information) leads to two extra unknown variables when solving FBSDEs.The above two obstacles could be overcome by proving that the asymmetric information structure is featured by the partially nested information structure and thus a linear form of the optimal controllers could be deduced.Thirdly, the study of the stabilization problem for the system involving additive noise is challenging, and merely a sufficient condition could be derived [24].It shall be dealt with by constructing an equivalent relationship between the systems involving and without additive noise.

The contribution of the work is summarized below.A complete solution to the problem of decentralized optimal control and stabilization for the interconnected system subject to asymmetric information is provided for the first time.For the finite-horizon case, the equivalent conditions for the unique solvability of the optimal control problem with asymmetric information are obtained by adopting the stochastic maximum principle.Based on the solution of the FBSDEs, the necessary and sufficient conditions for the decentralized optimal control problem are given, as well as the analytical expression for the closed-loop optimal controllers in terms of the solution to the proposed Riccati equation.For the infinite-horizon case, the necessary condition of the mean-square stabilization is presented for the system without additive noises.On the basis of the results and relationship between the two systems, the necessary and sufficient conditions for the mean-square boundedness of the system with additive noise are attained.

The remainder of the paper is structured as follows: In Section II, the finite-horizon decentralized optimal control problem is studied.The stabilization and optimal control problem for the infinite-horizon are investigated in Section III.Numerical examples are provided in Section IV.Concluding remarks are presented in Section V.Relevant proofs are detailed in the appendices.

The following notations and definitions will be used.Notations: Rndenotes then-dimensional Euclidean space.Imeans the unit matrix with the appropriate dimension.Δ ＞0 (or ≥0)denotes that Δ is a positive definite (or positive semidefinite)matrix.E stands for the mathematical expectation operator.Z(k) denotes the σ-algebra generated by the random variablezk.Tr(·) means the trace of a matrix, andA†denotes the Moore-Penrose inverse of matrixAandA'represents the transpose of the matrixA.0i×jrepresents a matrix of dimensionsi×jwith all zero elements and 0 means a zero matrix with compatible dimensions.F≐blkdiag{A,B,C,D} stands for a block diagonal matrix created by aligning the input matricesA,B,C,Dalong the diagonal ofF.

II.FINITE HORIZON CASE

A. Problem Formulation

The system to be studied is given by

whereQ≥0,R1≥0,R2≥0 andH≥0 are the weighting matrices with compatible dimensions.

Remark 1: It should be emphasized that the control weighting matrixRiin the cost functional (3) is positive semidefinite, which is a weaker condition than that of the work in [23]where the assumptionR＞0 was made.

In the interconnected system (2), the state of a subsystem is transmitted to another subsystem through the network connection with one step time required.Thus the information available to two controllers (subsystems) is as follows:

We introduce the following information sets:

Remark 2: In this paper, we assume there exists one step communication delay to guarantee the information propagation is no slower than the dynamics propagation through the plant.Actually, such an assumption of one step communication delay is commonly found in previous research [20], [22].

Problem 1: Find-measurable controlleru1kand Fk2-measurable controlleru2kto minimize the cost functional (3) subject to system (2).

Remark 3: Note that the proposed information structure is characterized by⊂Fk

j.It conforms to a partially nested information pattern, which indicates that the optimal control policy is linear (see Definition 3 and Theorem 2 in [25]).

Remark 4: The problem studied in this paper is different from the previous works [23], [26].In [26], the system with uncorrelated subsystem noises was dealt with, however, the results could not be extended to the case with correlated subsystem noises.By contrast, we remove the assumption that subsystem process noises are uncorrelated.Compared with[23], we aim to find the optimal closed-loop solution with the relaxer condition rather than an open-loop solution.

B. Equivalent Conditions of the Solvability of Problem 1

In this section, stochastic maximum principle is applied to(2) and (3) to transform the solvability of the Problem 1 into that of the FBSDEs.

Lemma 1: Assume Problem 1 could be solved uniquely, the optimal controllers meet the following equations:

where λksatisfies

Conversely, if FBSDEs (2) and (7)-(10) admit a unique solution, then Problem 1 could be solved uniquely.

Proof: The details of the proof are omitted here, which is similar to [27], [28].■

Obviously, we have that

And system (2) can be further transformed as

Lemma 2: Problem 1 is uniquely solvable if and only if the FBSDEs below are uniquely solvable:

whereR=blkdiag{R1,R2}, λkis as (9) and (10).

Proof: In view of Lemma 1, the key to verify Lemma 2 is establishing the equivalence of (7), (8) and (15)-(17).Taking conditional expectation on both sides of (7) and (8) with regard to, it follows:

Equation (15) could be obtained by augmentatingand.Then subtracting (18) from (7), we have (16).Similarly, subtracting (19) from (8), (17) follows.Therefore, (7) and (8)could be equivalently represented as (15)-(17) and Lemma 2 holds.■

C. Main Results

The major results shall be presented in three steps in this section: deduce the feedback forms of the controllers, give the optimal estimation and demonstrate the solution to Problem 1.The first part is shown now.

The estimation error covariance is as follows:

As shown in Lemma 2, to solve Problem 1 is converted into solving FBSDEs (9), (10), (14)-(17).To get the solution to FBSDEs and derive optimal closed-loop feedback gain explicitly, we introduce the following two backward recursion equations one of which is a Riccati equation:

where

Remark 5: Differently from [23] which derived an openloop optimal solution using a decomposition method for system state and control input based on noise history, Theorem 1 presents a closed-loop optimal solution to finite-horizon decentralized control problem subject to asymmetric information by applying the stochastic maximum principle.It is noted that the stochastic maximum principle, an effective and powerful tool in optimal control theory, is widely employed to address optimization problems, see [13], [27], [28].Moreover,the infinite-horizon stabilization problem will be dealt with in the next section, while it was not considered in [23].

III.STABILIZATION PROBLEM AND INFINITE CASE

A. Problem Formulation

The infinite-horizon stabilization problem will be investigated in this section.To begin with, the system (2) without additive noise is considered.Thus, the system studied can be expressed as

where the initial statex0is a Gaussian random vector with mean and covarianceand Σ0, respectively.The cost functional is given as

Remark 6: It should be emphasized that for the case without additive noise, theand (-) to be stated below are reduced respectively to:

Firstly, we introduce two definitions.

Then two standard assumptions are made below.The first guarantees the existence of unique pair of controllers, and the second is a standard assumption for the mean-square stabilization problem [29]:

Assumption 1:R1＞0,R2＞0 andQ=D′D≥0.

Assumption 2: (A,Q1/2) is exactly observable.

Before the main problem and results are given, the Lemma 3 is shown.

Lemma 3: With Assumptions 1 and 2, if there exist stabilizing controllers to make the system (35) mean-square stabilizable, the algebraic Riccati equation (38) admits a unique positive definite solutionP

where

Proof: Please see Appendix B.■

Remark 7: Noting that since the additive noise is not considered for the system here, the algebraic equations (38)-(40) in Lemma 3 are reduced to (38) and (41).

Next we will investigate the boundedness problem of the system (2).The associated performance is given by

B. Solution to Problem 2

The main results are presented in the following theorem.

Theorem 2: Under Assumptions 1 and 2, the system (2) is mean-square bounded if and only if there exists a unique positive definite solutionPto the algebraic equation (38).In this case, the stabilizing controllers satisfy

Moreover, the stabilizing controllers could minimize the cost functional (42) which is calculated as

Proof: Please see Appendix C.■

IV.NUMERICAL EXAMPLES

Consider a dual-motor parallel drive system as depicted in Fig.1.The dynamics of a single motor system can be described as

whereJ,θ,kvandkcdenote inertia moment, position output,viscous friction coefficient and Coulomb friction coefficient,respectively.s ign() is signum function,bis control gain,Tdis external disturbance, and Δkcand Δkvare parametric perturbations.

Fig.1.Overview of dual-motor drive system.

In this system, the dual-motor should achieve the goal of tracking a specified rotational angle while ensuring that the velocities of both motors tend to 0.Thus, a linearized model gives a sufficient description of the system behavior with these conditions.The discrete-time model for a dual-motor is given as (2) through linearing and one step forward discretization to (46).The matricesA,B¯1andB¯2are detailed as

Fig.2.Velocities of the two motors.

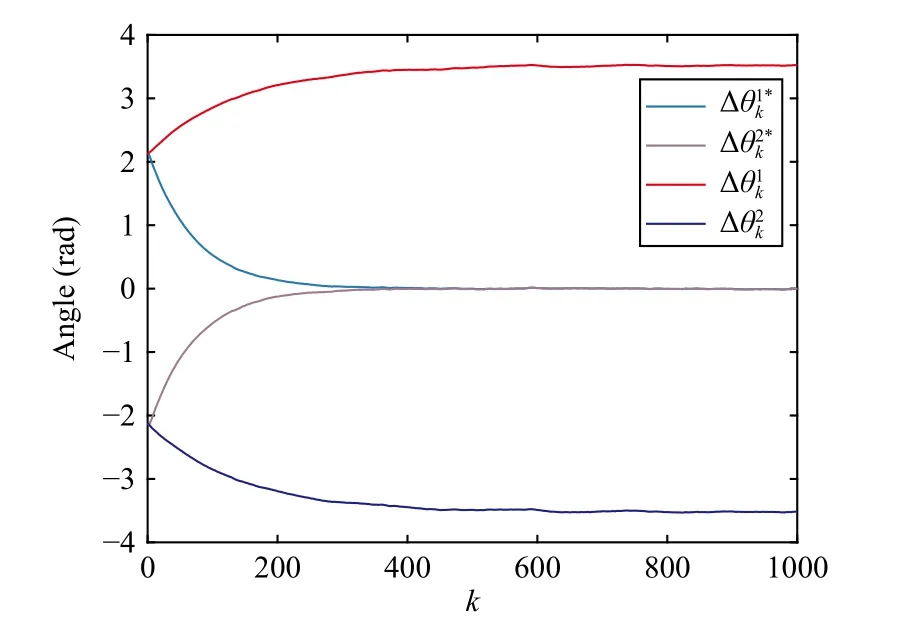
Fig.3.Comparison of tracking deviations with and without control.

V.CONCLUSION

The decentralized optimal control and stabilization problems for interconnected systems subject to asymmetric information have been investigated.Firstly, employing the stochastic maximum principle, an equivalent solvability condition for the problem of optimization has been presented in terms of FBSDEs.Based on the equivalence, a complete solution, the necessary and sufficient conditions and an closed-loop explicit form of controllers, has been obtained for the finite-horizon case.Furthermore, under standard assumptions, it has been shown that the system is mean-square bounded for the infinite-horizon case if and only if the algebraic Riccati equation admits a unique positive definite solution.In the future, our work will be extended to the multiplicative noises model,interconnected systenms withd-step delayed information sharing model and a large-scale system consisting of multi-subsystem withd-step delay.

APPENDIX A PROOF OF THEOREM 1

Using Lemma 2, we will show that (15)-(17) are uniquely solvable if and only if Υk,Υ1kand Υ2kare invertible fork=0,...,Nby induction.

Fork=N, from (10), (14), and (15), we have

which is the same as (33).Here ends the induction.

In brief, the uniquely solvability of (15)-(17) is transformed into the invertibility of Υkand Υik.Then employing Lemma 2, we conclude that Problem 1 has a unique solution if and only if Υkand Υikare invertible fork=N,...,0.Moreover, the optimal controllers are of the form of (31) and (32),and the solution to FBSDEs (9), (10), (14)-(17), are also verified as (33).

Finally, the optimal cost functional will be calculated using(31) and (33).

From (9), it yields

Adding fromk= 0 tok=Non both sides of (58), one has

From (59) with optimal controllers in (31) and (32), it follows:

Thus (34) is obtained.■

APPENDIX B PROOF OF LEMMA 3

Under Assumptions 1 and 2, suppose there exist controllersu1k=Γ1xkandu2k=Γ2xkwith constant matrices Γ1and Γ2to make closed-loop system (35) mean-square stabilizable, the assertion that there exists a unique positive definite solutionP

APPENDIX C PROOF OF THEOREM 2

Sufficient: With Assumptions 1 and 2, if there exists a positive definite solutionPto (38) we will demonstrate (2) is mean-square bounded.In virtue of (2), (43) and (44), one has

It is evident that the second term is constant, hence limk→∞E(xk)is mean-square bounded iff system (63) is mean-square stable.

with initial value θ0=x0.

Now we will demonstrate the mean-square stability of system (63).To this end, the Lyapunov function candidateFkis defined

In virtue of (38)-(40), one has

which indicates thatFkmonotonically decreases with respect tok.AsP＞0,Fk≥0 is bounded below, i.e,Fkis convergent.Selecting an integerlsatisfyingl＞0 , by adding fromk=ltok=l+Non both sides of above equation and lettingl→∞,one obtains

Along with Assumption 1, we have liml→∞E[θ′lθl]=0.Hence, we obtain that limk→∞E[x′kxk] is bounded, that is, (43)and (44) make system (2) mean-square bounded.Finally, we shall prove that (43) and (44) minimize the performance (42).Define