一种改进的局部均值伪近邻算法
李 毅,张德生,张 晓
西安理工大学理学院,西安 710054
分类[1]是数据挖掘中最重要的任务之一,它是通过对已知训练集进行学习,建立分类器预测未知样本标签的一种方法,在模式识别领域属于监督学习。目前,分类算法主要包括支持向量机[2]、决策树[3]、人工神经网络[4]、贝叶斯分类器[5]和KNN算法[6]等,其中KNN算法因具有较高的分类精度和易于实现等优点,在人脸识别[7]、故障检测[8]和医学研究[9]等领域得到了广泛应用。
KNN 算法的基本思想[10]是将待分类样本与训练样本之间的欧氏距离按升序排列,选取距离最小的k个近邻,将待分类样本分配给标签频率最高的类别。尽管KNN算法有许多优点,但仍有一些不足:KNN算法对近邻参数k比较敏感;选取近邻时未考虑样本的分布信息;采用单一的多数投票原则或最短距离原则进行分类决策。
针对KNN 算法存在的不足,研究学者提出了不同的改进方法[11-15]。文献[11]提出了一种新的基于距离加权最近邻规则的双加权投票方法(DWKNN),该算法降低了参数k的敏感性。文献[12]提出了利用距离加权来进行局部学习的伪最近邻规则,同时提出了基于局部平均向量和类统计量的非参数分类器(PNN),该方法减少了异常值对分类性能的影响。文献[13]对于PNN 算法中距离加权系数主观确定的问题,提出了一种基于BP神经网络的自适应伪最近邻分类算法(BPANN),降低了分类过程中主观因素带来的不确定性。文献[14]提出了一种基于局部均值的伪近邻算法(LMPNN),该算法使用k个局部均值向量代替k个最近邻,减少了KNN算法中异常值和维数对分类性能的影响。基于互近邻的思想,文献[15]提出了一种基于双向选择的伪近邻分类算法(BS-PNN),降低了噪声点对分类的影响。
不同于文献[11],LMPNN 算法计算各类的局部均值向量,使用伪近邻规则进行分类决策;文献[12]和[13]利用每类的k个最近邻计算伪近邻进行分类决策,而LMPNN 算法搜索每类的k个最近邻作为类原型,利用最近邻集合的k个局部均值向量找到各类基于局部均值的伪近邻,根据待测样本与新的伪近邻之间的加权距离进行分类,能够更加准确地找到伪近邻,提高了算法的分类准确率。LMPNN 算法虽取得了较好的分类效果,但仍存在以下不足:(1)在选取k个近邻时,只考虑待测样本到训练样本的距离,没有考虑样本的分布信息,并且没有从训练样本的角度确定待测样本是否为其k近邻;(2)对于分类测试样本,不同的多局部均值应该有不同的权重,但LMPNN 算法对每类的第i个局部均值向量主观赋予相同的权重1/i;(3)使用欧氏距离进行分类决策,不能较好地反映局部均值对分类的作用。
针对LMPNN 算法的上述不足,本文进行了改进,提出了一种改进的局部均值伪近邻算法(ⅠPLMPNN)。
(1)引入了双层搜索规则查找待测样本的双层近邻集,提高了近邻集的选择质量;
(2)引入了注意力机制计算局部均值点与待测样本之间的距离加权系数,体现了局部均值向量对待测样本的重要程度;
(3)提出了新的多调和平均距离进行分类决策,降低了噪声点的影响和近邻参数k的敏感性。
1 预备知识
1.1 符号说明
本文常用的符号见表1。

表1 符号说明Table 1 Symbol description
1.2 LMPNN算法
在P维特征空间中,假定有训练样本集T={y1,y2,…,yN},其类标签为,给定一个待测样本x,LMPNN算法的步骤如下:
算法1LMPNN算法
输入:待测样本x,训练集T={y1,y2,…,yN},类标号,类cj对应的训练集Tj={y|l(y)=cj},近邻个数k。
输出:待测样本x的类标号。
步骤1计算待测样本x到Tj中每个样本y的欧氏距离:
将得到的距离按升序排列,取前k个近邻记为y(1),y(2),…,y(k)。
步骤2计算待测样本x在Tj中的第i个局部均值向量:
步骤3在Tj中,对k个近邻点所对应的局部均值点按照到待测样本x的距离升序排列,并为第i个局部均值点赋予对应的权值:
步骤4查找x在Tj中的伪近邻点,x到的距离d()被定义为k个局部均值点到x的欧氏距离的加权总和,即:
步骤5预测待测样本x所属类:
2 本文算法
2.1 双层搜索规则
LMPNN算法采用式(1)确定待测样本的近邻集,仅考虑了待测样本和训练样本之间的距离,对噪声点仍然敏感。针对这一问题,本文引入双层搜索规则查找待测样本的近邻集合,提高近邻集的选择质量,降低噪声点的影响。根据步骤1至步骤4查找待测样本的双层近邻集[16]。
步骤1对于待测样本x,其在训练样本集Tj的第一层近邻集为:
即,用传统的近邻规则在Tj中查找待测样本x的k近邻所形成的集合。
步骤2对于待测样本x,其在训练样本集Tj的第二层近邻集为:
其中,rNN1st(x)是NN1st(x)的半径,即x到NN1st(x)中第k个近邻的距离。
步骤3对于待测样本x,其在训练样本集Tj的扩展近邻集为:
其中,c是NN2nd(x)的质心。
步骤4对于待测样本x,其在训练样本集Tj的双层近邻集为:
其中,(y)代表集合T*=Tj∪{x} 中y的kb个近邻形成的集合,kb一般不小于k。计算(x)中的k*个近邻与x的欧氏距离,按照升序排列记为y͂(1),y͂(2),…。需要指出的是表示集合的基数。k*一般受kb取值影响,其值可能大于k,也可能不超过k。由双层近邻集(x)计算x在Tj中的第i个局部均值向量:
2.2 注意力机制
LMPNN 算法式(4)中的由权值Wi和局部均值点到x的距离两部分的乘积组成。然而,由式(3)计算的权值Wi对任意的k个近邻点均是固定的,使得LMPNN 算法不能得到较优的距离加权值。由此本文引入注意力机制对其进行改进,考虑每个局部均值向量对待测样本分类的影响。
注意力机制模型[17]能够根据信息的重要程度赋予相应的权重。注意力机制的步骤主要分为以下三步:首先,使用评分函数计算两样本点的相似度;其次,利用softmax 函数归一化,使其成为一个和为1 的概率分布,得到注意力系数;最后,根据注意力系数和相应点的加权和得到注意力值。根据注意力机制,设置Tj中第i个局部均值点(见式(10))对应的权值为:
其中
反映局部均值点和待测样本x的相似度。
2.3 多调和平均距离
针对LMPNN算法式(4)中距离对近邻参数k以及噪声点均敏感的问题,本文在已有的调和平均距离[18]基础上,提出一种新的多调和平均距离,定义如下。
Tj中第i个局部均值向量到待测样本x的多调和平均距离为:
其中,表示Tj中第r(r=1,2,…,i)个局部均值向量,表示待测样本x与的欧氏距离。
式(14)中用替代式(13)中的d(x,y),将每类中的k*个近邻用k*个局部均值向量替代。具体分析如下:
其中,y͂(1),y͂(2),…,y͂(k*)为使用双层搜索规则得到x在Tj中的k*个近邻。
d(x,y)易受到单个近邻的影响,若近邻集合中有噪声点,分类结果因噪声点的影响可能导致待测样本的误分类。由式(15)可知,考虑了x与的差分向量,并且使用u͂rj代替近邻点,在进行分类决策时受单个近邻点的影响较小,降低了噪声点的影响。另外,式(14)的i相较于式(13)中的k是变化的,从而能降低近邻参数k的敏感性。
2.4 IPLMPNN算法
本文算法的基本思想为:首先,在Tj中通过双层搜索规则选取待测样本x的双层近邻集。使用筛选后的近邻计算局部均值向量。其次,引入注意力机制计算注意力系数,利用式(11)为多局部均值向量分配不同的权重。最后,使用新的多调和平均距离式(14)进行分类决策。由此,提出了ⅠPLMPNN算法,具体步骤见算法2。
算法2ⅠPLMPNN算法
输入:待测样本x,训练集T={y1,y2,…,yN},类标号,类cj对应的训练集Tj={y|l(y)=cj},第一层近邻个数k。
输出:待测样本x的类标号。
步骤1根据双层搜索规则查找待测样本x在Tj中的k*近邻,表示为。计算中的k*个近邻到x的欧氏距离,按照升序排列为y͂(1),y͂(2),…,y͂(k*)。
步骤2根据(10)式计算待测样本x在Tj中的第i个局部均值向量,令形成的集合为
步骤3在Tj中,根据式(11)和式(12)计算每个局部均值向量对待测样本x的影响权重。
步骤4在Tj中,根据式(14)计算待测样本x到局部均值向量的多调和平均距离。
步骤5查找x在Tj中的伪近邻点,x到的距离被定义为k*个局部均值点到x的调和平均距离的加权和,即:
步骤6预测待测样本x的类标号:
ⅠPLMPNN 算法的流程图如图1 所示。首先,将样本数据预处理,查找待测样本的双层近邻集;然后,由局部均值向量和待测样本计算注意力系数,得到距离权重系数;最后,由新的多调和平均距离计算得到伪近邻点,对待测样本进行分类。
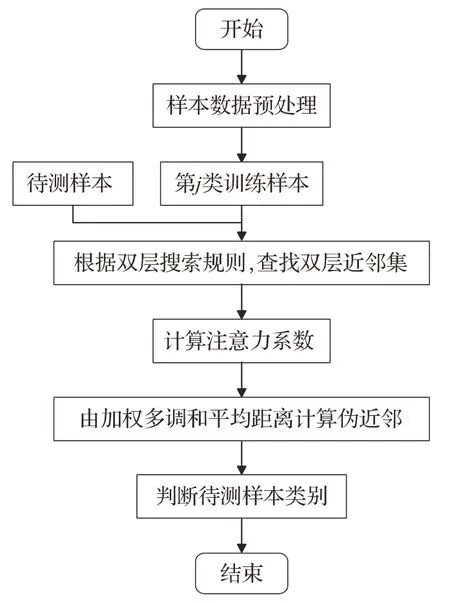
图1 ⅠPLMPNN算法流程图Fig.1 ⅠPLMPNN algorithm flow chart
2.5 算法复杂度分析
假设数据集的规模为N,特征维数为P,近邻个数为k,类别个数为M。ⅠPLMPNN算法的时间复杂度主要来源于以下5 个方面:(1)计算待测样本到每类训练样本的欧氏距离,找到k个近邻,时间复杂度为O(NP+Nk);(2)使用双层搜索规则查找待测样本的双层最近邻,时间复杂度为O((k2+k)M);(3)计算每类的k个局部均值向量,得到k个局部均值向量与待测样本之间的多调和平均距离,时间复杂度为O(MPk+M(1+k)k);(4)将注意力权重分配给每类的局部均值向量,得到每个类的伪近邻点,时间复杂度为O(Mk+MPk);(5)使用决策函数确定待测样本的类别,时间复杂度为O(M) 。因此,ⅠPLMPNN 算法总的时间复杂度为O(NP+Nk+MPk+Mk2)。
3 实验与分析
3.1 数据集
为了验证ⅠPLMPNN 算法的有效性,选择UCⅠ和KEEL 中的14 个数据集(如表2 所示)进行实验。所有实验均在MATLAB R2017b环境下完成。

表2 数据集Table 2 Data sets
3.2 实验结果与分析
实验以分类准确率为评价标准。对样本数量较小的数据集采用10次3折或5折交叉验证法,对样本数量较大的数据集采用10 次10 折交叉验证法,最终将实验得到的准确率平均值作为分类结果。对近邻参数k逐一取值1,2,…,15,采用交叉验证法得到每个k值所对应的平均准确率,将最高的平均准确率所对应的k值选择为最优k值。
3.2.1 实验参数设置
实验1对于ⅠPLMPNN算法步骤1中的参数kb,不同于传统近邻规则中的近邻参数k,kb一般大于k需通过实验确定。这里,取kb=k,kb=1.2k,kb=1.4k,kb=1.6k,kb=1.8k,kb=2.0k,利用ⅠPLMPNN算法对表2的数据集进行实验,实验结果如表3 所示,加粗数字表示各数据集的最优值。

表3 k 与kb 在不同关系下的分类准确率Table 3 Classification accuracy under different relationships of k and kb单位:%
表3 的实验结果表明kb在6 种相应取值下,ⅠPLMPNN 算法分别在4 个,7 个,5 个,4 个,3 个,2 个数据集上得到了最高的分类准确率。并且kb=1.2k在14个数据集上的平均准确率为86.72%,在6种取值中排名第一。实验结果表明kb=1.2k有最好的分类性能,所以在实验2 和实验3 中设置kb=1.2k,以实现更好的分类效果。
3.2.2 IPLMPNN算法在最优k 值下的性能分析
实验2为了评估ⅠPLMPNN算法在最优k值下的分类性能,将KNN[8]、DWKNN[11]、PNN[12]、MLM-KHNN[18]、KGNN[19]、RCKNCN[20]、DC-LAKNN[21]和LMPNN[14]算法与ⅠPLMPNN算法的平均准确率进行对比。得到的平均分类准确率如表4 所示,加粗数字表示9 种算法的最优值。需要说明的是,其他8种算法的平均准确率也是最优k值下对应的结果(k=1,2,…,15)。

表4 最优k 值下ⅠPLMPNN算法与其他8种算法的平均准确率Table 4 Average accuracy of ⅠPLMPNN and other eight algorithms corresponding to optimal k value 单位:%
表4 的结果表明,除Heart、Ⅰris、Letter 和Thyroid 数据集外,ⅠPLMPNN算法在其他10个数据集上得到了最高的平均分类准确率。特别在Glass、Ⅰonosphere、Seeds和Sonar 这4 个数据集上的分类准确率较LMPNN 算法有了明显提升。在Letter 和Thyroid 数据集上取得最高准确率的是RCKNCN算法,其结果为96.37%和95.40%,分别比ⅠPLMPNN 算法高0.05 个百分点和0.22 个百分点。在Heart 和Ⅰris 数据集上取得最高准确率的分别是MLM-KHNN 算法和LMPNN 算法,其准确率分别为80.16%、95.13%,比ⅠPLMPNN 算法高0.13 个百分点和0.12 个百分点。虽然ⅠPLMPNN 算法在这4 个数据集上的准确率略低,但仍高于大多数对比算法。并且ⅠPLMPNN 算法在14 个数据集中获得了最高的平均准确率86.37%,与其他8种算法相比有明显的优势。
3.2.3 IPLMPNN算法在不同k 值下的性能分析
实验3为了验证ⅠPLMPNN 算法在不同k值下的分类性能,将8 种对比算法与ⅠPLMPNN 算法在10 次交叉验证中得到的平均分类准确率进行比较。利用表2的Ⅰonosphere、Seeds、Segment、Glass4 个数据集进行仿真实验。图2为9种算法的平均分类准确率折线图。

图2 不同算法在4个数据集上随着变化的k 值的平均分类准确率Fig.2 Average accuracy of each algorithm with variation of k values for four data sets
从图2可以看出,当k <5 时,ⅠPLMPNN算法较其他对比算法更为陡峭,准确率增长趋势更大。当k在5到10之间时,ⅠPLMPNN算法在Ⅰonosphere、Segment、Glass数据集上呈现出较为平稳的变化趋势,在Seeds 数据集上呈现增长趋势。当k >10 时,KNN、DWKNN、PNN、KGNN算法的准确率随着k值的增大而减小,LMPNN、MLM-KHNN、DC-LAKNN、ⅠPLMPNN 算法的准确率较为平稳,且略有增长,RCKNCN 算法在Ⅰonosphere 和Glass数据集上变化较为平稳,在Segment数据集上准确率随着k值的增大而增大,而在Seeds 数据集上准确率呈现下降趋势。说明了9种算法中ⅠPLMPNN算法在不同近邻参数k下的分类性能是具有优势的,降低了参数k的敏感性。
4 结束语
针对LMPNN算法存在的不足,本文对其进行了改进,提出了一种改进的局部均值伪近邻算法(ⅠPLMPNN)。ⅠPLMPNN算法首先通过引入新的近邻选取规则选取待测样本的高质量近邻点,然后基于注意力机制计算各类的距离加权系数,最后使用改进的多调和平均距离作为新的分类决策规则,降低了近邻参数k对算法的影响。实验结果表明,ⅠPLMPNN 算法在分类准确率上取得了令人满意的结果。由于ⅠPLMPNN算法的时间复杂度较高,因此,下一步的研究工作将提高ⅠPLMPNN算法的计算效率,并将改进的算法应用到实际问题中。

