深度神经网络平均场理论综述
颜梦玫,杨冬平
(1.福州大学 先进制造学院,福建 泉州 362000;2.中国科学院海西研究院 泉州装备制造研究中心,福建 泉州 362200;3.之江实验室 混合增强智能研究中心,杭州 311101)
0 引言
深度神经网络(Deep Neural Network,DNN)最初主要应用于参数初始化的预训练过程[1],后来利用具有深度的卷积神经网络(Convolutional Neural Network,CNN)识别图像[2]。DNN 吸引了众多研究者的关注,由此掀起了深度学习的热潮。然而,尽管DNN 在应用领域取得了显著的成功,但其背后的决策机理仍不够明确。目前,深度学习方法仍然是一门高度实践的艺术,充满许多启发式的技巧,并非一门精确的科学。这一缺陷对于金融、医疗、公共安全和国防等领域通常是致命的[3]。因此,需要构建一个成熟的DNN 理论指导深度学习中的广泛工程应用,进而优化深度学习算法。尽管近年来在深度学习理论方面取得一些成效,但大部分工作专注研究单个隐藏层网络,深度网络的理论在很大程度上仍悬而未决。
DNN 与传统的浅层网络的本质区别在于网络的深度,而DNN 成功的一个关键因素在于它的高表达性:一方面,它可以紧凑地以一种浅层网络无法做到的方式表达输入空间的高度复杂函数。此外,DNN 可以将输入空间中的高度弯曲流形在隐含层空间中解耦为扁平流形,有利于简单地线性读出。这些DNN 的直觉理解完全可以通过现有的平均场理论(Mean Field Theory,MFT)来描述、分析和探讨[4]。MFT 不仅可用于描述与分析特定DNN 的训练过程[5],还可以探讨DNN 的泛化性能及关键因素[6]。这些理论研究成果,让人们看到MFT 在构建一个统一理解DNN 运行机制理论框架中是一个非常重要的基本理论方法。
近年来,美国斯坦福大学Ganguli 团队[4]利用动力学平均场理论(Dynamic Mean Field Theory,DMFT)和黎曼几何[7]研究了DNN 的高表达性:信息在DNN 中有效传播机制和全局曲率随深度指数增长。基于DMFT 的信息有效传播机制最早起源于20 世纪80 年代Sompolinsky 等[8]开创性提出的随机神经网络模型,通过DMFT 分析发现系统随参数变化可以从有序态相变到混沌态,以及发现混沌边缘(Edge of Chaos,EoC)的相变点。Ganguli 团队利用离散时间的随机神经网络模型[9],将该模型中的时间点替换成DNN 中网络的层数号,发现网络在EoC 的参数下呈现出更高的表达能力。
从MFT 的角度研究DNN 的初始化,发现了两个影响网络训练的性质:前向信息传播对于不同样本的表达性(Expressivity)和反向梯度传播的可训练性(Trainability)。在随机DNN 中,由表达性和可训练性确定的超参数范围已经得到了实验验证[10-15],当网络初始化在EoC 附近时,其表达性和测试精度都会较高。此外,研究发现,误差的有效反向传播需要网络参数满足所谓的动力等距(Dynamical Isometry,DI)条件[16-18]。在这种条件下,研究人员成功训练了在没有批量归一化和残差网络结构帮助下的单纯一万层的CNN[11]。
对于随机初始化的DNN,通过MFT 更进一步地发现,在网络无限宽的极限(网络被过度参数化)下[19]:如果只训练网络的最后一层,可以用神经网络高斯过程(Neural Network Gaussian Process,NNGP)核的核无岭(Ridgeless)回归描述网络的训练[20],DNN 与NNGP 的内在联系使人们可以确切地用贝叶斯推断回归训练DNN;如果训练所有的层,可以用神经正切核(Neural Tangent Kernel,NTK)[5]描述,这种描述使人们可以直接研究DNN 中无穷维的函数空间和超级复杂的参数空间。
事实上,深度学习中的关键泛化现象也发生在核方法中:要理解深度学习中的泛化,必须先理解核方法中的泛化。哈佛大学Pehlevan 团队[6]利用MFT 推导出了核回归的平均泛化误差的解析表达式,提出DNN 泛化的关键因素在于核与任务的本征谱匹配度。这个理论揭示了各种泛化现象,包括训练过程中泛化误差表现出的非单调行为。该理论进一步指出,核回归的归纳偏置为学习曲线的非单调行为提供了机理上的理解,并为所谓的“双重下降”现象[21]提供见解。
因此,MFT 为研究DNN 的运行机理提供了一个非常重要的基本理论手段。MFT 能从理论角度初步探索深度学习中的初始化、训练过程和泛化机制,进而可以在工程上指导深度学习算法进行改进和优化[22]。然而,目前国内基于深度学习理论的相关科研人员缺少对DNN 在深度学习中取得显著成功的内在机理的广泛认识,特别是MFT 在理解DNN运行机制中发挥的基础性作用。本文对DNN 现有MFT 的研究进行了整理和回顾,从网络初始化、训练过程和网络泛化性能这三个方面的理论理解入手,并在各种人工神经网络(Artificial Neural Network,ANN)中进行了相关对比分析,关于DNN 内在机理的理解与逻辑框架如图1 所示。此外,本文还分析了该领域仍存在的难点并展望未来研究趋势,为进一步深入研究深度学习理论提供参考。
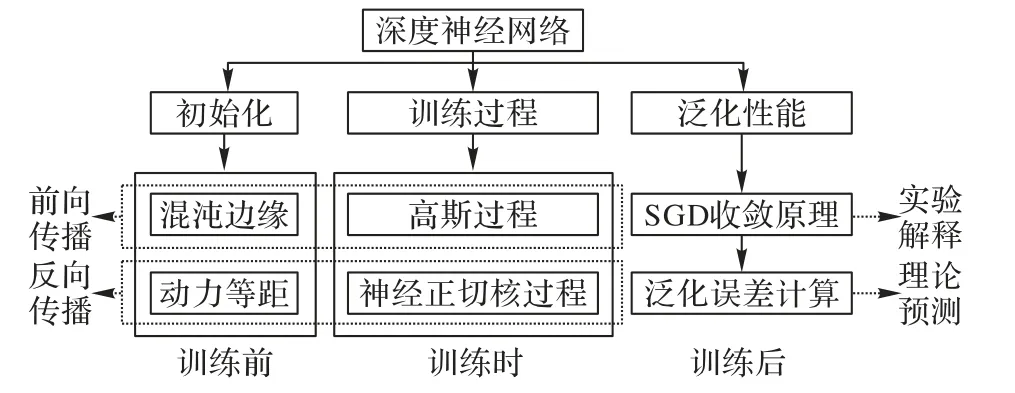
图1 MFT在理解DNN内在机理的研究框架Fig.1 Research framework of MFT in understanding intrinsic mechanisms of DNN
1 深度神经网络初始化
DNN 初始化从以下两个特性分析:前向信息传播对于不同样本的表达性和反向梯度传播的可训练性。这两种特性分别对应DNN 中的EoC 和DI,如图2 所示。
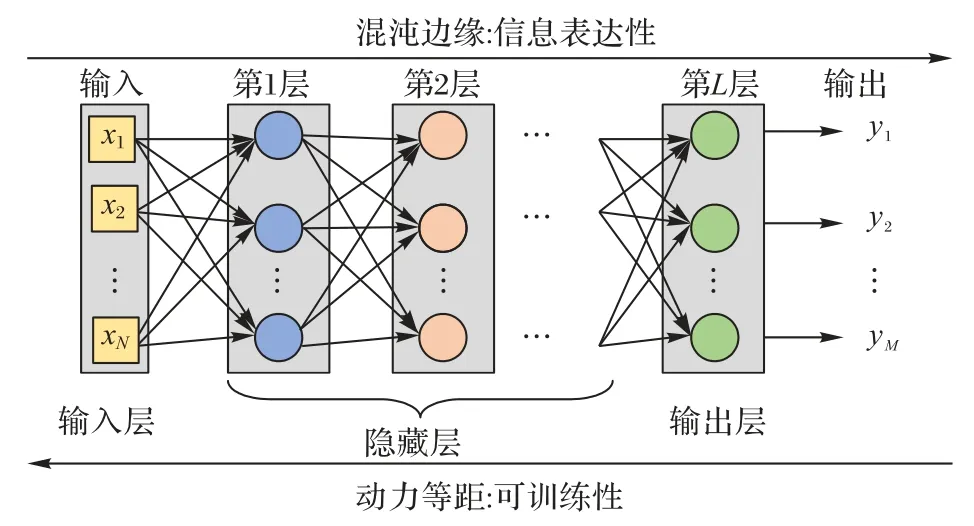
图2 DNN前向信息传播和反向梯度传播的两个特性Fig.2 Two characteristics of forward information propagation and backward gradient propagation in DNN
1.1 混沌边缘
1.1.1 随机网络动力学
通过Sompolinsky 等[8]研究的随机非对称耦合相互作用的N个非线性神经元网络的连续时间动态模型,当N→∞时,运用自洽MFT,可以发现在增益参数g>0 时的临界值处发生有序态到混沌态的相变。EoC 相变点处的系统状态具有无穷长时间关联的性质,该网络的动力学可由N个耦合的一阶微分方程描述[8](符号定义见表1),即

表1 相关变量定义与对比Tab.1 Definition and comparison of relevant variables
该性质在具有离散时间动力学的系统中也成立。Molgedey 等[9]在此基础上将动态模型的时间t离散化,研究在外部噪声影响下的随机非对称全连接网络的离散时间动力学,即
1.1.2 神经网络动力学
用神经网络层数l取代离散的时间变量t,用权重矩阵W代替突触连接Jij,每层l有Nl个神经元,由输入x0引发的前馈动力学(符号定义见表1)即为:
其中ϕ为非线性激活函数。在每层宽度足够大的极限下,即Nl≫1,单输入向量x0的长度q0在网络传播中会发生变化。对于大Nl,可以得到ql的高斯分布迭代式:
同样,两个输入x0,1和x0,2的高斯积分形式可表示为:
其中:z1和z2为独立的标准高斯变量为u1和u2相关高斯变量的协方差矩阵。

图3 有序态-混沌态的相变图Fig.3 Ordered state-chaotic state phase transition diagram
可以直观地把χ(σw,σb)作为判断临界的序参量。控制有序态-混沌态的参数对比见表2。

表2 控制相变的参数Tab.2 Parameters controlling phase transition
总的来说,这是EoC 性质在神经网络中的重要理论分析,结合MFT 深入分析了信号在通过大型随机前馈网络的确定性性质,揭示了由权重和偏置的统计函数控制的有序态到混沌态相变的存在,并且发现在相变点上有限深度演化的暂态混沌是深度随机网络具有指数表达性的基础。
1.1.3 混沌边缘的具体应用
EoC在深度神经网络参数初始化中起重要作用。Mishkin等[23]认为一个好的初始化条件很有必要:初始化参数设置得当,网络可以训练得很深,训练精度在EoC 附近甚至可达到100%。表3 显示了EoC 在不同网络的作用,其中对比了有无EoC情况下达到目标准确率所需要的迭代次数。从表3中可以明显看出,使用EoC初始化时,所需迭代次数更少;在没有EoC下,无论目标准确率如何设置,所需迭代次数都比有EoC时多。虽然全卷积网络(Fully Convolutional Network,FCN)、卷积神经网络(Convolutional Neural Network,CNN)等网络在EoC 附近初始化可以训练得很深,但对于Dropout 网络,它的最大网络层数的设定是有上限的[10]。

表3 EoC在各种人工神经网络中的作用Tab.3 Roles of EoC in various ANNs
给定损失函数为L 时,反向传播方程可表示为:
由式(7)可知,χ(σw,σb)控制有序态-混沌态的相变,可由ξ∇是否发散表示相变,ξ∇与χ、g控制相变的详细取值对比如表2 所示。
若梯度不独立,边界参数需修正[25]。由MFT 可知:
前面的ξ∇通过计算得出(6ξ2),而在梯度不独立的假设下,可通过计算整体的得到新的ξ∇(12ξ1与12ξ2)。
1.2 混沌边缘特性
1.2.1 表达性与复杂性
神经网络的表达能力取决于它的网络架构,更深的网络可表达更复杂的功能。对于分段线性函数网络,比如ReLU(Rectified Linear Unit)激活函数网络,它的网络表达能力可以用不同线性区域数度量,也可以通过将网络调整为接近线性状态使网络具有高表达能力[26]。Serra 等[27]从理论和实验的角度进行相关验证。
1.2.2 信息传播与反向传播
通过MFT 研究随机权重和偏差分布的未训练的神经网络动力学行为,可以定义一种可训练的深度尺度,并且该深度尺度自然而然地限制了随机网络传播信号的最大深度[10]。由此可见,神经网络的随机权重初始化在深度学习分析中起着重要作用。尽管这些网络由随机矩阵构建,可以用随机矩阵理论(Random Matrix Theory,RMT)分析,但对于非线性网络,现有的数学结果并不能直接利用。为此,Pennington 等[28]在逐点(Pointwise)非线性化神经网络中利用自由概率论方法将RMT 应用于深度神经网络。另外,Yang等[26]的理论表明,梯度信号随深度呈指数增长,无法通过调整初始权重方差或调整非线性激活函数消除爆炸性梯度。他们认为批量归一化本身就是梯度爆炸的原因,对于没有跳跃连接(Skip connections)的普通批量归一化无法在DNN 训练。虽然无法完全消除梯度爆炸,但可以尽可能调整网络为线性状态以减少梯度爆炸的影响,提高没有残差连接的深度归一化网络的可训练性。
1.2.3 网络可训练能力
经典的前馈神经网络在前向输入传播和反向梯度传播时,都随深度表现出指数行为。其中前向动力学指数行为导致输入空间几何形状快速崩溃,反向动力学指数行为导致梯度急剧消失或爆炸。在EoC 假设下,网络在稳定态和混沌态之间的边界徘徊,保持输入空间的几何形状和梯度信息流,从而增强网络的可训练能力。Yang 等[29]将此理念用于残差网络,从理论和经验上证明了Xavier 或He 等[30]的方案等常见初始化对于残差网络并非最优,因为决定最优初始化的方差取决于网络深度,与EoC 相关。Hayou 等[31]从不同激活函数网络的层面上,用MFT 分析了EoC 对可训练神经网络的随机初始化的作用。
1.3 动力等距
1.3.1 Jacobian矩阵
DNN 能很好进行训练的原因是:反向传播过程中的梯度既没消失也未发生爆炸,维持在一种稳定的状态。因此,需逐步剖析梯度更新与传播的内在机理,旨在改进与优化现有网络算法。对于损失函数为L 的网络,它的梯度链式更新可以表示为:
其中:xL表示最后一层的输入,xl表示第l层的输入。要想梯度更新能顺利从最后一层传到前面层,需要保证的值在1 附近,Saxe 等[17]将初步定义为一种端到端Jacobian 矩阵,即
该Jacobian 矩阵捕获了输入扰动经过网络传播对输出的影响。
DI 概念首次被Saxe 等[17]提出,即满足输入-输出Jacobian 矩阵的奇异值分布在1 附近:
其中:Dl是对角矩阵,它的矩阵元素满足对于Jacobian 矩阵谱的理论计算,需要用到自由概率论中的S变换将Dl和Wl拆成单独两项计算,具体计算过程如图4 所示,上部分框图表示Wl的S 变换过程,下部分框图表示最终Jacobian 矩阵JJT的S 逆变换过程。为简便计算,考虑求解矩阵JJT的谱分布,其特征值开根号即为Jacobian 矩阵的特征值。其中:①表示Stieltjes transform;②得到矩生成函数MX;③为功能函数的逆变换过程;④为S 变换;⑤为S 变换过程的合并:
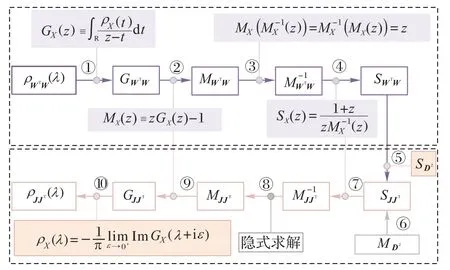
图4 Jacobian矩阵谱计算流程Fig.4 Computing flow of Jacobian matrix spectrum
如果A和B为两个相互独立的随机矩阵,它们随机矩阵乘积的 S 变换就是它们 S 变换的乘积,即SAB(z)=SA(z)SB(z)。⑥为Dl的S变换的中间求解过程,与③和④相同。⑦得到JJT的逆矩生成函数。⑧因为JJT矩阵特别庞大且复杂,已经不能用式子表示,只能通过隐式求解来数值计算矩阵JJT的矩生成函数。⑨类似于过程②。通过⑩则可以求得最终矩阵JJT的谱密度表现形式。最后,根据不同激活函数ϕ的设定,可以将Jacobian 矩阵谱的形态划分为Bernoulli 类和Smooth 类[32]两类。对于某些特殊的权重矩阵,可以利用随机矩阵理论求解特征谱,比如随机高斯非对称实矩阵谱分布服从Girko 定律(整圆率)[33],对称则服从半圆率[34];如果是稀疏矩阵或者是厄米与非厄米矩阵,可以采用空腔方法或复本方法求解。
1.3.2 动力等距的具体应用
由前文可知:DNN 的前向传播体现了高表达性,可通过EoC 性质刻画;而反向传播则更注重网络的可训练性,梯度传播的稳定性可用DI 刻画,即梯度既不会消失也不会爆炸。这两种结论已经在全连接网络(Fully Connected Network,FCN)[10]、CNN[11]、循环神经网络(Recurrent Neural Network,RNN)[12]和残差神经网络(ResNets)[13]等得到实验验证,当满足DI 时,网络的训练速度会特别快[17],在没有批量归一化和残差结构帮助下,还能成功训练一万层CNN[11]。表4 中列举了使用DI 后与原网络的测试精度对比,其中“—”表示没有DI 条件时网络不能训练。
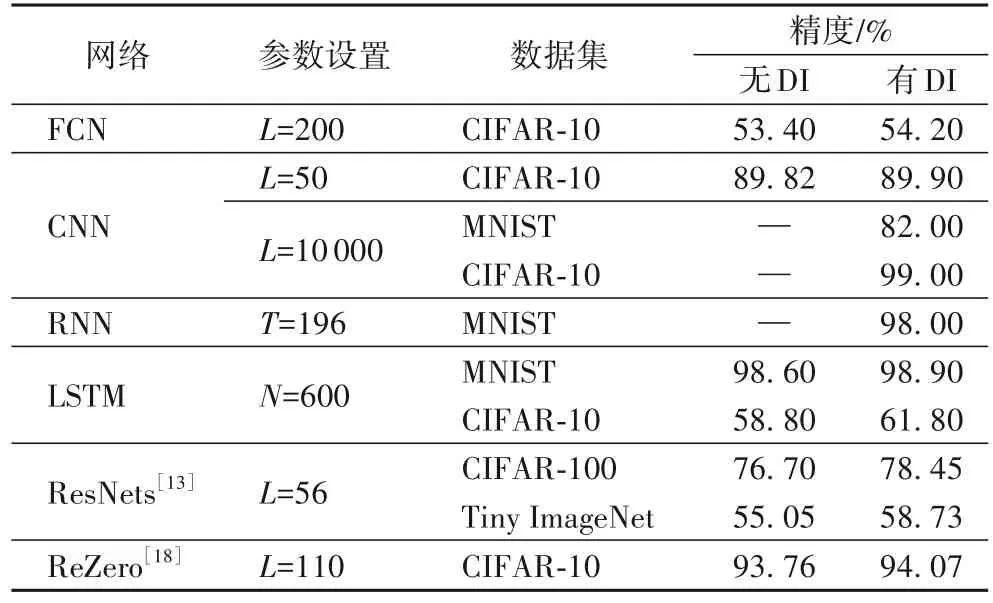
表4 DI对各种人工神经网络测试精度的提升作用Tab.4 Role of DI in improvement of test accuracies for various ANNs
对于Jacobian 矩阵谱,不同网络的不同Dl可用自由概率论求解,具体对比分析如表5 所示。其中满足DI 正交化的方式大致可以分为三种:直接随机权重矩阵正交化、设定权重矩阵S 变换后的特征值为0,以及Jacobian 矩阵谱的特征值为1 或-1。另外Yang 等还从数学层面对神经网络中的平均场性质进行了进一步的理论分析,比如,EoC 处的残差网络[29]、批量归一化中的平均场[26]和无限宽的超参数网络[35]等。
满足DI 的DNN 可通过以下两个方面构建:
1)随机正交化。对于深度线性网络,可以通过正交权重初始化实现DI,这已被证明可以显著提高学习速度,比没有实现DI 的网络学习速度快几个量级[17]。在非线性情况下,通过自由概率论的强大工具分析计算深度网络输入输出Jacobian 行列式的整个奇异值分布。在此基础上,Xiao 等[11]提出了一种用于生成随机初始正交卷积核算法,能训练一万层或更多层的Vanilla CNN。Rodríguez 等[36]在正则化基础上,研究了一种局部强制特征正交性的新型正则化技术(OrthoReg),在特征去相关中施加局部约束消除负相关特征权重之间的干扰,使正则化器能达到更高的去相关边界,更有效地减少过拟合。这种正则化技术可以直接运用于权重上并适用于全卷积神经网络。此外,Xie 等[37]利用不同滤波器组之间的正交性的正则化器变体加强网络的可训练性,还结合了残差结构在ImageNet 数据集实现了相关性能比较。对于较难训练的RNN,Arjovsky 等[38]构建了一种归一化权重矩阵新架构,使它的特征值的绝对值恰好为1 以优化网络训练过程。另一种更简单的解决方案是使用单位(Identity)矩阵或其缩放(Scaled)版本初始化循环权重矩阵[39]。在DNN中,Li 等[40]介绍了一种正交DNN,建立了一个新的泛化误差界。在CNN 中也有相关正交性的应用[41]。Guo 等[42]提出一种新的正交特征变换Ortho-GConv,用于增强图神经网络(Graph Neural Network,GNN)主干,以稳定模型训练并提高模型的泛化性能。
2)等距惩罚项。虽然可以直接设置正交化条件以满足DI 初始化,但在训练过程中很难保证,需要对损失函数设置相关DI 的约束条件,使网络在训练过程中也一直保持DI 性质。初始化、归一化和残差连接被认为是训练非常深的CNN并获得最先进性能的三种不可或缺的技术,文献[43]中通过在初始化和训练期间强制卷积核接近等距,也可以训练没有归一化或残差连接的深度Vanilla CNN。
2 深度神经网络训练过程
用MFT 研究DNN 的过参数化网络,可以将前向初始化近似为高斯过程,反向梯度训练过程近似为NTK。
2.1 过参数化网络
在神经网络的经验学习过程中,训练误差和泛化误差不能同时兼顾,它们之间为此消彼长的关系。但是Belkin 等[21]发现当参数足够多时,训练误差和泛化误差之间可以保持一种平衡。因此,过参数化,即在极限条件下网络宽度趋向无穷,从某种程度上具有一定优势。Huang 等[44]从不同数据集的层面,对比分析了过参数化的优势,发现参数越多的网络具有更高的测试精度和更强的泛化能力。Arora 等[45]揭示了两层网络在过参数化情况下对任意数据进行泛化的原因。Du 等[46]认为两层神经网络成功的原因之一是随机初始化的一阶方法,如梯度下降,即使目标函数是非凸的和非光滑的,也可以在训练过程中达到零损失的状态[47]。虽然具有随机初始化的基于梯度的算法可以收敛至过参数化的神经网络训练损失函数的全局最小值,但是保证全局收敛的神经网络宽度条件非常严格。Zou 等[48]采用一种更温和(Milder)的过参数化条件,对DNN 训练过程中的随机梯度下降(Stochastic Gradient Descent,SGD)的全局收敛性进行了改进分析。
2.2 高斯过程
过参数化的网络易于平均场理论分析。因为在参数趋于无穷的极限条件下可以用现有的一些理论解释,例如,热力学极限定律、统计力学等。另外,参数多使得知道的先决条件也多,可以用贝叶斯推断网络的参数[19],即使计算量太大也可以用变分方法或者蒙特卡洛采样大致估计。
在中心极限定理下,无限宽的随机连接神经网络等价于高斯过程,不管有多少网络层数,不用进行任何训练也可以对DNN 进行贝叶斯推断。高斯过程对于分类函数的每一个类都可以提供具体的先验分布,它联系神经网络和核方法,将表示网络输出与输出之间关系的核矩阵叫作NNGP 核。对于式(4)所示网络,若为单层神经网络,则可以得到网络输出的分布为即高斯核的均值为μ1、方差为K1,每个变量之间都与i无关。此时其中C(x,x')的引入来源于Neal等[19],所以单层网络的NNGP 核可以表示为:
对于深层网络,它的NNGP 核表示为:
协方差矩阵可进一步简写为:
然而,不同的激活函数ϕ会生成不同的NNGP 核,对于ReLU 非线性函数,它的Fϕ为确定的arccosine 核;而对于Tanh,Fϕ只能采用线性插值的方法数值求解。
给定数据集D={(x1,t1),(x2,t2),…,(xn,tn)},(x,t)为输入-目标,用函数h(x)对测试点x*进行贝叶斯预测,并且网络输出值为h≡(h1,h2,…,hn),多元高斯先验分布则可表示为h*,h|x*,x∼N (0,K),其中协方差矩阵:
得到NNGP 核就可得到所有训练数据之间的关系和先验,采用贝叶斯推断预测新的测试数据的网络输出,所以此时只需计算新产生的,不同神经网络的NNGP 核公式对比如表6 所示。

表6 各种人工神经网络的NNGP公式Tab.6 NNGP formulas for various ANNs
2.3 高斯过程等价网络
通过研究具有多个隐藏层的随机全连接宽前馈网络与具有递归内核定义的高斯过程之间的关系,发现随着网络宽度增加,表示网络的随机分布函数逐步收敛到高斯过程[50]。除FCN 外,在无限多卷积滤波器限制下的CNN 也可以看作高斯过程[51],Novak 等[52]还对比了有无池化层的多层CNN 的类似等价性。对于贝叶斯神经网络(Bayesian Neural Network,BNN),即便其中一些隐藏层(称为“瓶颈”)保持在有限宽度,也可以收敛到高斯过程[53]。Pretorius 等[54]则研究了噪声正则化(例如Dropout)对NNGP 的影响,并将它们的行为与噪声正则化DNN 中的信号传播理论联系起来。上述相关网络的高斯过程近似等价是在无限宽的条件下,Lee 等[55]对无限宽网络和有限宽网络的NNGP 对比研究,并通过对权重衰减进行逐层缩放(Layer-wise scaling),改进了有限宽网络中的泛化能力。
尽管高斯过程理论具有吸引力,但它却不能捕获特征学习(Feature learning),而特征学习却是理解可训练网络的关键要素。Naveh 等[56]考虑在大型训练集上使用噪声梯度下降训练DNN,推导出自洽的高斯过程理论以解释强大的有限DNN 和它的特征学习效果。另外,也有从热力学理论的角度分析有限超参数化CNN 的特征学习,并也适用于有限宽DNN[57]。
2.4 神经正切核
对于DNN 动力学的研究还有另外一个分支:从NTK 角度观察。NNGP 核是关于神经网络输出与输出之间的协方差矩阵,而NTK 则是在此基础上将神经网络的训练过程与核方法联系起来研究梯度与梯度之间的关系。NTK 由Jacot等[5]首次提出,他们认为神经网络在参数空间的梯度下降与在NTK 下函数空间的梯度下降等效,所以NTK 可以用于描述神经网络中无限宽DNN 在梯度下降训练过程中演化的核,而这个核在无限宽极限下会趋于一个确定的核,并且在梯度下降的过程中保持不变[58]。针对全批量梯度下降训练的神经网络[46],可以对输出进行一阶泰勒展开,用一个接近无限宽网络的线性模型近似[59],因此该无限宽网络的动力学行为可以用一个常微分方程(Ordinary Differential Equation,ODE)表述,这种无限宽极限的动力学就叫作NTK域(Regime)或惰性训练域(Lazy training regime)。
另外,Arora 等[60]提出了一种高效算法计算卷积架构的NTK,即CNTK(Convolutional Neural Tangent Kernel),文献[61]结合CNN 高斯过程内核的回归对CNTK 算法进行了改进,提高了内核的性能;然而,上述文献作者只研究了浅层网络的无限宽极限(NTK 域)影响。Hayou 等[62]发现EoC 初始化对于NTK 也有一定的好处,并将NTK 与MFT 联系起来,对DNN 中的SGD 训练和NTK 训练进行了对比。
2.4.1 核的定义
考虑FCN 的输入为h0(x;θ)=x,每一层的输出为为 经过激活函数后,网络最后一层输出为fθ(x)表示为:
其中FL:RP→F,代表将参数θ映射到F空间中的函数fθ,P表示网络参数量。
对于任意L层的初始化网络来说当N1,N2,…,NL-1→∞时,NTK 中的ΘL收敛于一个确定极限核,即
其中dNL代表维度为NL,与高斯核有关的递归关系如下:
2.4.2 线性网络动力学
用ft(x) ≡表示神经网络在t时刻的输出,令ωt≡θt-θ0,将输出网络进行一阶泰勒展开可得:
定义的损失函数为L,梯度流(Gradient flow)则可表示为=-η∇θL,根据链式法则有:
因此,神经网络的动力学可由一个ODE 描述,无限宽的网络就是一个关于参数的线性模型,它可以证明在梯度下降过程中NTK 始终保持不变且具有稳定性,损失函数最终也会收敛为全局最小值,而且网络非常宽时,权重在训练过程中和初始权重相比变化也不大。针对不同的神经网络并参考文献[63-64]中的模型定义,NTK 的公式对比总结如表7所示。

表7 各种人工神经网络的NTK公式Tab.7 NTK formulas for various ANNs
2.4.3 网络的训练过程特征
NTK 使用梯度流对DNN 训练的这种动力学在无限宽的极限下称作NTK 域或惰性训练域。NTK 网络参数的初始化为高斯初始化,而对于DI,它的网络初始化可看作正交初始化。在浅层网络中,无论是在DI 条件下,还是处于NTK 域中,正交初始化和高斯初始化的效果都一样。但是当打破该NTK 领域时,即增大学习率或固定网络宽度以增大网络深度时,由于DI 对DNN 训练的提升作用,此时网络将不再处于NTK 域中[65]。
总的来说,NTK 在无限宽神经网络下有两个非常有用且重要的性质:一是在无限宽网络中,若参数θ0在以某种分布进行初始化,那么在该初始值下的NTKΘ(θ0)是一个确定的函数,不管初始值为多少,最终总会收敛到一个确定的核函数,且与初始化无关;二是无限宽网络中的Θ(θt)不会随着网络训练而变化,即训练中参数的改变并不会引起核函数的变化。基于此,可以将无限宽网络的训练过程理解为简单的关于核函数的梯度下降法,其中核函数固定,只取决于网络结构和激活函数等。在Neal[19]的结论基础上,可以将这个用梯度下降收敛的极值概率分布看作一个随机过程。总之,NTK针对梯度下降法提出,是关于梯度核的收敛,是训练过程的一种表现形式;而高斯过程是初始化网络收敛到高斯核,并未涉及训练过程。
2.4.4 神经正切核的具体应用
将神经网络的训练过程与核回归过程建立等价关系后,就可以解决无限宽神经网络在实际中的表现问题,此时只需测试使用NTK 的核回归预测器即可。Arora 等[60]在CIFAR-10 上对图像分类数据集测试了NTK,因为对于图像数据集需要使用CNN 才能获得良好的性能,所以扩展NTK 构造适用于CNN 的CNTK,并测试了它们在CIFAR-10 上的性能。实验发现CNTK 是非常强大的内核,而且全局平均池化可以显著提高CNN 和CNTK 的分类准确性,据此认为许多改善神经网络性能的技术在某种意义上通用。同样,除了全局平均池化外,希望其他技巧也可以提高NTK 内核性能,比如批量归一化或者残差连接层,NTK 不仅应用在FNN、CNN 和RNN[66]上,也应用于GNN[63],这几种网络的NTK 性能对比如表8 所示。对于NTK 的Python 代码运算,可以直接导入相关函数包[67]或者使用JAX[68],另外还可以通过Jacobian 构造和分解NTK 向量积等方法[69]加速有限宽网络的NTK 计算。此外,Yang[70]从随机神经网络收敛到高斯过程,再到通过NTK预测梯度下降的训练动态,在数学上重新推导了经典的随机矩阵结果。人们还设计了Tensor programs 来单独阐述任意RNN 架构网络的高斯过程[71]、任意架构的NTK[64]、NTK 训练动力学的泛化性能[72],以及无限宽网络的特征学习[73]。对于DNN 中的可训练性和泛化性,Xiao 等[74]从NTK 的角度制定了一系列架构的可训练和泛化的必要条件。
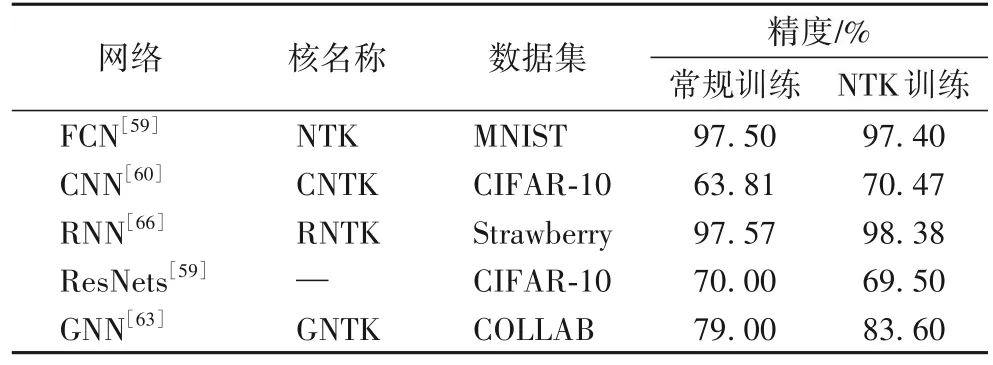
表8 各种人工神经网络的NTK性能Tab.8 Performance of NTK in various ANNs
3 深度神经网络泛化性能
第2 章中介绍了过参数化网络的优势,可以在无限宽极限下,将网络初始化后信息在网络中的传递过程用NNGP 核表示,而网络参数的训练过程用NTK 表示,并在一定程度上能描述有限宽网络。本章将着重介绍过参数化可以带来好的泛化能力的原因、影响泛化性能的因素以及泛化性能的预测。
Arora 等[45]通过研究两层网络的过度参数化,利用依赖于数据复杂性的度量,改进了独立于网络规模的泛化界限。此外,根据Belkin 等[21]发现的过参数化后的训练误差-泛化误差关系,SGD 方法可能隐含地限制了训练网络的复杂性(图5)。一些实验现象也表明,当SGD 的极小值处于很宽的能量景观(Landscape)平面时网络会有很强的泛化能力[75]。对于简单两层神经网络,通过适当缩放利用分布动力学(Distributional Dynamics,DD)的特定非线性偏微方程(Partial Differential Equation,PDE)捕获SGD 动力学,进而解释SGD 收敛到具有近乎理想泛化误差的网络的原因[76]。另外,从统计物理中能量与熵的角度进行剖析[77],理论推导证实了实验上的直观现象,其中批量大小(Batchsize)影响了SGD 的随机性,随机噪声会自发地使SGD 走向宽的极小值。
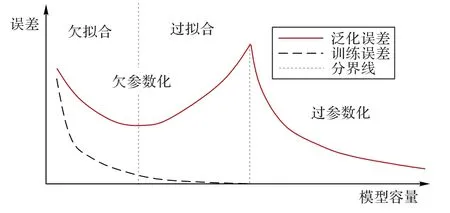
图5 训练误差与泛化误差曲线示意图Fig.5 Schematic diagram of training error and generalization error curves
3.1 泛化性能影响因素
人工神经网络的泛化能力通常是指它识别未经训练的样本的能力。泛化问题主要可以分为两大类:一是“弱泛化”,可理解为“鲁棒性(Robustness)”,即训练数据与测试数据来自同一分布;二是“强泛化”,可看作一种“理解(Understanding)”能力,即训练数据与测试数据分布不同,需要使它在训练集上学习的模型在测试集上也表现良好。影响网络泛化性能的因素主要如下:
1)网络结构。实现网络复杂性与样本复杂性之间的平衡,最主要的方法就是剪枝(Pruning),是决策树学习算法中对付“过拟合”的主要手段,它的基本策略包括预剪枝(Prepruning)和后剪枝(Post-pruning)[78]。由于后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情况下它的泛化性能优于预剪枝。虽然剪枝网络可以主动去掉一些分支降低过拟合风险,但是有些时候也会加剧过拟合。例如,当通过网络修剪增加模型稀疏性时,测试性能因网络过拟合变差,即使减轻过拟合可以提升测试性能,但最后也会因忘记有用信息而变得更差。He 等[79]把网络剪枝有时加剧过拟合的现象称为“稀疏双重下降”。针对该现象,他们还通过彩票假设机制提出了一种新的学习距离解释,即稀疏模型的学习距离曲线(从初始参数到最终参数)可能与稀疏双重下降的曲线很好地相关。
2)训练样本。神经网络作为一种非参数模型,所有信息都来源于训练样本集,训练样本集对泛化性能的影响有时超过网络结构复杂性对泛化性能的影响[80-81]。在DNN 的训练过程中使用模型参数的梯度信噪比(Gradient Signal-to-Noise Ratio,GSNR),即梯度的平方均值和方差与数据分布的比值,可以建立模型参数的GSNR 与泛化差距之间的定量关系:较大的GSNR 会导致更好的泛化性能[82]。另外,通过泛化鸿沟(Generalization gap)预测训练数据和网络参数的泛化差距,得到可以实现更好泛化的新的训练损失函数[83]。对于使用反向传播算法训练的前馈分层神经网络,通过在训练样本中引入加性噪声也可以增强神经网络泛化能力[84]。Vyas 等[85]从自然数据集出发,分析了NTK 泛化的局限性,研究认为真实网络和NTK 之间的本质区别不仅是几个百分点测试精度的差距。
3)学习机制。学习策略对网络机制的泛化性能影响较为复杂,主要源于鞍点和局部极值问题。在相同学习误差和网络结构条件下,泛化误差因到达不同的局部极值点而不同。可以通过约束网络学习模型(约束条件与目标函数)、全局与局部最优算法选择、训练终止准则和初始权重与归一化等改善前馈网络泛化性能。对于随机高斯的权重初始化,很少有工作考虑到特征各向异性的影响,大多数都是假设高斯权重为独立同分布。而Pehlevan 等[86]则据此推导出具有多层高斯特征模型的学习曲线,并且表明第一层特征之间存在相关性可以帮助网络泛化,而后几层的结构通常有害,阐明了权重结构如何影响一类简单的可解模型中的泛化。除此之外,在损失函数加入惩罚项是当前比较常用的正则化优化方式,相关正则化技术还有Dropout[87]、权值噪声和激活噪声等。
3.2 泛化性能理论
3.2.1 SGD的最优值收敛
定义损失函数
其中R(θ)为正则化函数,yi为网络输出,由SGD 引起的网络参数更新可以表示为:
其中:ηt表示学习率,Bt表示随机从训练集中选取数据的批量大小。根据Langevin 方程以及梯度流的定义,可以将SGD写成下述形式,即
此时,η(t)表示一种随机噪声,表示所有数据点同时输入与批量输入对网络输出产生影响的差异,如下所示:
过参数化网络拥有好的泛化性,可能得益于SGD 的作用,Jastrzębski 等[88]认为影响SGD 最小值有3 个因素,即学习率、批量尺寸和梯度协方差,并且认为学习率与批量大小的比值是影响SGD 动态和最终最小值宽度的关键决定因素,比率值越高,最小值范围越宽,泛化效果越好。
SGD 的下降趋势取决于噪声的方向及大小。当网络的训练过程收敛到一定状态时,可分两种情况分析:一种是因为掉进了宽的局部最小值,可以通过额外添加噪声[89]使梯度继续下降,朝着更低极小值走去;另一种是处于鞍点,就需要新的算法逃离鞍点[90]。
3.2.2 内核与泛化误差
给定P个观察样本输入xμ服从分布p(x),假设样本的标签yμ带有噪声其中关于p(x)平方可积,εμ为添加的零均值噪声,方差满足关系对上述P个样本的数据集,核回归问题[6]可以描述为:
其中:λ为岭(Ridge)参数,H 是由其再生核K(x,x')和输入分布p(x)唯一确定的再生核希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)[91],表示RKHS 内积,希尔伯特范数惩罚项控制f的复杂性[92]。
泛化误差,即估计量f*与数据分布和数据集的平均真实目标值之间的均方误差,可表示为:
Eg从平均上衡量所学习的函数与从同一分布采样的未知(和已知)数据的目标一致程度。式(33)的分析可以使用无序系统统计物理学中的复本方法[93]。
利用Mercer 分解方法,将核K(x,x')分解成关于正交的特征函数项{ϕρ}:
特征值{ηρ}和特征向量{ϕρ}构成RKHS 的完整基。通过特征图(Feature map),可将式(34)右边项设置为正交基,用于计算任何核和数据分布的核回归泛化误差。另外,还可以用该泛化误差公式很好地描述低至几个样本数据集的平均学习曲线,由于训练集的随机抽样,学习曲线的走势会随着数据集样本量的增加而衰减。对式(33)的解进行实验分析,一个直接的观察是它的谱偏差:若误差沿特征函数的收敛越快,则在没有噪声限制下的特征值就越高[6]。
基于上述核回归泛化理论,可以计算从浅层FCN 到深度CNN 等DNN 训练中的泛化差距(Gap)。Misiakiewicz 等[94]用RKHS 的内核特征计算高维单层卷积核中的任何给定函数的渐进泛化误差。
3.3 泛化性能内核预测
在无限宽网络极限下,基于高斯过程和NTK 过程的内核演化可以预测网络的泛化性能。Simon 等[91]推导出一种预测核回归泛化的新理论,不仅可以准确预测测试均方误差,还可以预测网络学习函数的所有一阶和二阶统计量,并且可以准确预测有限宽网络。针对不同架构的DNN,还可以利用重尾自正则化(Heavy-Tailed Self-Regularization,HTSR)[95],在不查看测试数据的情况下预测何种DNN 具有最佳测试准确性。Bordelon 等[96]通过自洽动力场理论分析了用梯度流训练的无限宽度神经网络的特征学习。此外,他们还分析了使用梯度下降和生物学相关机制(反馈对齐)训练的无限宽深度网络,并认为DMFT 能比较学习规则中的特征和预测动态,内核的演化也可以用DMFT 自洽地决定[97]。Cohen 等[98]则利用类物理学的方法,准确地预测了足够深的DNN 在多项式回归问题上的学习曲线。
Canatar 等[99]分析内核与网络目标函数的对齐方式(Kernel alignment),用内核表示DNN 学习的有用数据,并在实验上研究了训练期间由层数演化的内核,当内核可由浅层到较深层进行表示时,网络可更好地进行泛化。此外,Pehlevan 团队[6]通过研究核回归的泛化误差描述了相关无限宽过参数化的神经网络的泛化能力,并且使用统计力学相关技术推导出了适用于任何内核和数据分布的泛化误差的解析表达式,结合真实和合成数据集以及多种内核,阐明了内核回归的归纳偏置,并用简单函数解释数据表征了内核与学习任务的兼容性。
4 未来方向
深度神经网络平均场理论被广泛用于指导深度学习中的工程设计,但在DNN 中的初始化、训练过程以及泛化预测这3 个阶段上依然存在一定的挑战:
1)初始化阶段。尽管MFT 在DNN 的应用中取得了一定成效,还可以和统计力学相结合,从能量的角度出发理解DNN 的随机初始化及表征能力[100],但在训练过程中可能会破坏好的初始化,这时该如何拯救尚未可知。已有研究从正则化的角度让网络在训练过程中尽量保持好的网络状态,如上述提到的加入等距惩罚项等方法,但还未达到完全可以保障的效果。要想真正地探究DNN 的初始化机制,EoC 和DI这样的初始化理论可能还远远不够,特别是在EoC 和DI 之外是否存在更好的算法可以弥补不理想的初始化状态,这对发展更加可靠的DNN 具有重要的指导意义。因此,利用MFT 进一步深入研究DNN 初始化的作用机制是非常有意义的方向之一。
2)训练阶段。既然NTK 可以在理论上描述任意深度L的神经网络,那为何实际实验中进行的却是浅层网络?一个可能的原因是较大的网络宽度意味着影响输出的神经元很多,连接这些神经元的权重发生一点细微变化都可能导致网络输出变化很大;另一种可能的原因是对于初始化不满足训练条件的DNN,即不满足EoC 和DI 条件,梯度不能从网络的最后一层反向传播至输入层。另外,对于有限宽网络,NTK也并不能完全适用[85],实际实验中真实的网络宽度也不可能接近无穷,NTK 理论终归和实验有偏差,还需改善现有理论,以更好地衡量有限宽或深度网络的训练能力。
3)泛化阶段。虽然泛化理论在预测方面取得了一定的突破,但也有局限性:第一,该理论需要在完整数据集上进行核的特征分解,导致计算量庞大;第二,对于DNN 的内核描述受到限制,不能捕获更多有用的深度学习现象;第三,该理论使用高斯近似假设,即使实验验证无误,但放宽高斯近似假设后对于新的实验见解仍未知。另外,Pehlevan 的泛化理论基于核回归,而对于非核回归等问题目前还没有类似于核回归泛化理论的理论。特别是当深度神经网络在做特征学习时处于非NTK 区域,目前的泛化理论研究还处于初期阶段,任重而道远。
5 结语
本文从随机网络的动力学模型出发,回顾并综述了DNN的初始化MFT 理论及其对DNN 学习性能的重要性,以及过参数化和无限宽极限下的各种MFT 理论,介绍了训练过程中收敛性和泛化性的相关MFT 理论进展。目前对DNN 的工作原理的理解还很粗浅,要想解析DNN 的内部机理开发和改进工程算法,还需要更多的理论实验探索,从更深层次的角度用MFT 理论理解DNN 的工作原理。

