基于DREAM_ZS 算法的EIT 电阻率反演方法研究
李颖 ,马重蕾 ,赵营鸽 ,王冠雄 ,郝虎鹏
(1.河北工业大学 生命科学与健康工程学院,天津 300130;2.河北工业大学 河北省生物电磁与神经工程重点实验室,天津 300130;3.河北工业大学 天津市生物电工与智能健康重点实验室,天津 300130;4.新乡医学院三全学院 智能医学工程学院,河南 新乡 453003)
电阻抗成像(EIT)的基本原理是在人体表面施加安全的激励电流,测量由此电流产生的目标表面的电压信号,重构出被测目标内部的阻抗图像分布[1].由于它具有操作简单、成本低廉、无损伤等特点,在医学成像方面获得了广泛的关注.在对EIT 的研究中,为了简化计算,通常假设生物组织的阻抗分布是不变的,但实际情况中,阻抗分布是变化的,这就导致图像重建结果是不确定的[2].因此研究电阻率的变化对EIT逆问题的影响具有重要的意义.
目前,EIT逆问题求解的很多算法都是在确定性框架下的,如牛顿迭代类方法、神经网络类算法、进化类全局优化算法等,以及各类算法的改进形式,这些算法可对目标内的阻抗分布进行重构,并试图提高重构图像的分辨率[3-5],但它们对于电阻率分布的不确定性欠考虑.为了使逆问题计算结果更加全面、精确,考虑不确定性因素是必要的.对逆问题进行不确定性量化可以归纳为统计推断问题,贝叶斯方法是概率统计范畴的方法,它不仅可以对参数进行反演,还能对输出结果进行不确定性量化,因此在逆问题求解中的应用很广泛[6-10].
贝叶斯方法是一种结合先验信息和似然函数来获得后验分布的方法.在一些非线性的复杂模型中,计算后验分布时往往难以形成解析式,通常采用有效的抽样算法来获得稳定的后验分布.马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)算法凭借其良好的收敛优势成为目前应用最为广泛的抽样算法[11].MCMC算法是一种通过构建马尔科夫链来获得随机参数样本的间接抽样方法,在复杂的非线性模型中,需要大量反复地进行抽样计算,虽然可以取得较好的效果,但其计算效率很低,尤其是面对高维度参数时[12].为了解决这个问题,可以在MCMC 算法中引入自适应的思想,例如自适应Metropolis 算法和延迟拒绝自适应Metropolis 算法等[13-14],但这些算法都是单链运行.有研究者提出一种差分进化自适应Metropolis 算法,被命名为DREAM 算法,它是一种利用多条隐马尔科夫链并列运行的改进MCMC 算法,利用差分进化使其收敛和计算速度得到了很大的提升,而进一步发展的自适应差分进化Metropolis 抽样(Differential Evolution Adaptive Metropolis,DREAM_ZS)算法在DREAM 算法基础上进行了改进,在参数反演及其不确定性量化方面得到了广泛的应用[15-16].
另外,在贝叶斯方法的实现中,对后验分布的计算需要调用大量与正问题模型相关的似然函数计算,正问题原始模型计算耗时过长会大大影响整体效率,所以采用计算效率高的模型来替代原始模型是很有必要的.常用的替代模型有神经网络类模型[17-18]、高斯过程回归模型[19]、克里金(Kriging)模型[20]等.反向传播(Back Propagation,BP)神经网络由于其非线性映射能力强、计算效率高,被广泛应用于复杂非线性模型的替代模型.
本文针对EIT 逆问题中电阻率分布不确定的情况,采用BP 神经网络模型替代求解EIT 正问题的有限元模型,基于贝叶斯理论,采用DREAM_ZS算法求得电阻率的后验概率密度,从而对EIT 逆问题的不确定性进行量化.
1 理论与方法
1.1 EIT逆问题的求解模型
EIT研究的是一个特殊的电流场问题,可以将待测目标看作成一个导体,电流的流动受场域内电导率分布的影响[21].EIT 数学物理模型可以用一个二阶椭圆型偏微分方程来表示[22].设物体所在区域为Ω,边界为Γ,假设物体内部无源,仅考虑电导率σ分布时,有
EIT 逆问题是根据测得的边界电压分布反演内部阻抗分布.由于电流密度是阻抗分布的函数,所以EIT 逆问题是个非线性问题.在实际测量中,电极数量和电流注入方式是有限的,这就导致了从边界电极获得的信息不足以确定目标内部的阻抗分布,而且,电极位置对阻抗分布的敏感性不同.这些使得EIT逆问题成为一个高度病态的非线性问题.
由于EIT 逆问题的不适定性和病态性十分严重,在求解时需要引入先验信息.结合了先验信息和观测数据的贝叶斯方法可以量化逆问题解的不确定性,有些情况下可以降低不适定问题的不适定程度[10].
1.2 贝叶斯反演的基本原理及方法
贝叶斯理论描述的是由果及因,即利用事情发生后的结果推出导致事情发生的原因.它的数学表达式为
式中,p(m|d)为后验分布,p(d|m)为似然函数,p(m)为先验分布,p(d)为测量数据的概率密度.在参数反演问题中m为待反演参数,d为测量数据,由于p(d)与反演参数无关,所以可看成一个常量.那么上式也可以表示为
可见参数的后验分布完全是由先验分布以及似然函数决定的.先验参数分布是由人的日常生活经验或者科学家及权威科研资料所给出的.似然函数表征的是理论数据与实测数据之间的差异程度.最常用的似然函数是高斯似然函数,即假设误差向量δi服从独立标准正态分布,其似然函数计算表达式为
式中,L(x)为似然函数,xi为反演参数,(fxi)为正问题计算结果,即模拟计算数据,udi为实测数据,nd为参数数目.
MCMC 算法通常用于非线性模型的后验分布计算.MCMC 算法通过构造一条具有转移特性的隐马尔科夫链来探寻未知参数的后验分布空间。假设该链为x={xt;t>0},在抽样计算过程中,该链在t+1时刻的概率值p(xt+1)仅仅只与t时刻的概率值p(xt)有关.此转移特性表示为
当该马尔科夫链的转移概率满足此特性时,说明该链已经达到可靠的收敛程度,此时该链的分布即为参数的稳定后验分布.
但MCMC 算法在面对高维参数模型时,其收敛性和收敛速度都受到了很大的限制.DREAM_ZS 是一种多链MCMC 算法,它在DREAM 算法的基础上增加了简化离散和组合搜索参数空间的扩展功能,可以通过差分进化、子空间探索、从过去状态采样、斯诺克更新和多重尝试Metropolis 采样的组合来有效地探索高维和多模态后验概率密度,具有较强的收敛能力和鲁棒性[23].DREAM_ZS算法基本步骤为:
1)根据n个待反演参数的先验分布抽样出N个初始样本,作为初始种群(k=1),代入正演模型,利用式(3)、式(4)计算样本的后验概率分布.
2)对第k代每一个个体进行变异操作.
式 中,vk为变异 后个体,γ为缩放因子,一 般γ=为模型参数,ε为方差.
3)按照交叉概率CR进行交叉操作,之后判断是否取代新样本.若U≤1 -CR,则令未变异样本点取代变异后的样本点,反之不取代.
式中,U是一个取值在0~1 的随机数,交叉概率CR∈[0,1],根据抽样自适应性发生变化.
4)对新样本计算接受概率.若接受新样本,则取变异后的样本点;若不接受,保持原位置状态,使平行序列继续进化.
式中:q为用于评价的马尔科夫链的条数;B为链内方差;为q条马尔科夫链均值的方差;为uj的均值;W为q条马尔科夫链方差Sj的均值.若值达标,表明马尔科夫链已可靠收敛;若不达标,则继续进行序列进化.
1.3 基于贝叶斯框架的EIT参数反演
对于EIT 参数反演,电阻率ρ和测量的电压U被假设为具有某种联合概率的多元随机变量.贝叶斯方法的目标是在给定电位测量值的情况下求解电阻率分布的后验概率.
使用贝叶斯定理,电阻率后验概率表示为p(ρ|U),表征测量电位数据的似然函数表示为p(U|ρ),p(ρ)表示为电阻率的先验分布,U(ρ)为EIT正问题计算得到的模拟电位值,udi为理论电位值.引入高斯误差项ε~N(μδi,σδi2)来表征模拟电位值和实测电位值之间的关系.
综上所述,基于贝叶斯框架的EIT 参数反演有以下步骤:
1)根据电阻率ρ的先验分布产生N组初始样本;
2)将样本值输入EIT 正问题计算模型,计算出理论电位值U(ρ);
3)引入高斯误差项,根据式(13)计算似然函数p(U|ρ);
4)求解式(14)得出电阻率的后验分布函数p(ρ|U);
5)采用DREAM_ZS抽样算法对后验分布进行抽样,得出各个电阻率的边缘后验密度;
6)对电阻率的反演结果进行不确定性分析.
1.4 EIT正问题计算的BP神经网络替代模型
在EIT 正问题的研究中,往往采用有限元法进行求解.如果在EIT 模型中反复调用有限元来进行计算,将会导致计算效率很低.BP 神经网络结构简单、非线性映射能力强,可以明显提高计算速度,故本文采用BP神经网络来替代有限元模型.
BP 神经网络主要由三部分构成:输入层、隐含层和输出层[25].在神经网络的训练过程中进行了两种计算,一种是前向计算,另一种是逆向反馈计算.
具体地,前向计算过程为
式中,ωij表示节点i与节点j之间的权值,bj为节点j的阈值,xi为节点输入值,f为激活函数,yj为节点输出值.
逆向反馈过程为
式中,dj为假定的输出结果,e(ω,b)表示误差函数,表示修正后的权值,表示修正后的阈值.当达到目标误差期望函数时,BP神经网络训练完成.
2 仿真模型的构建与正问题计算
在EIT 正问题的计算过程中,采用有限元网络对模型进行剖分,仿真模型如图1 和图2 所示.图1为四层同心圆模型,由内到外分别代表大脑、脑脊液、颅骨和头皮,每层的电阻率一致,其参考值如表1所示[26].图2 为高维参数模型,它是将圆域剖分成64个小三角单元,每一个单元的电阻率都不同,总计64个电阻率值.两个仿真模型均采用16 个电极,均匀放置于目标表面,目标外界半径为10 cm.在仿真实验中,设置激励电流为1 mA,50 kHz.
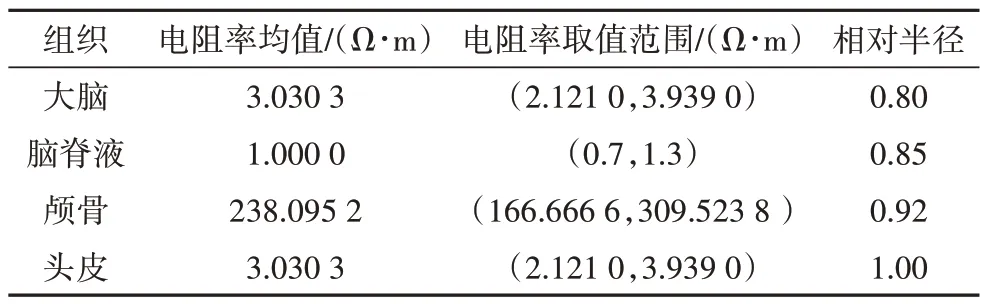
表1 四层同心圆模型参数取值表Tab.1 Parameter values of the four-layer concentric circle model

图1 四层同心圆模型Fig.1 Four-layer concentric circle model.
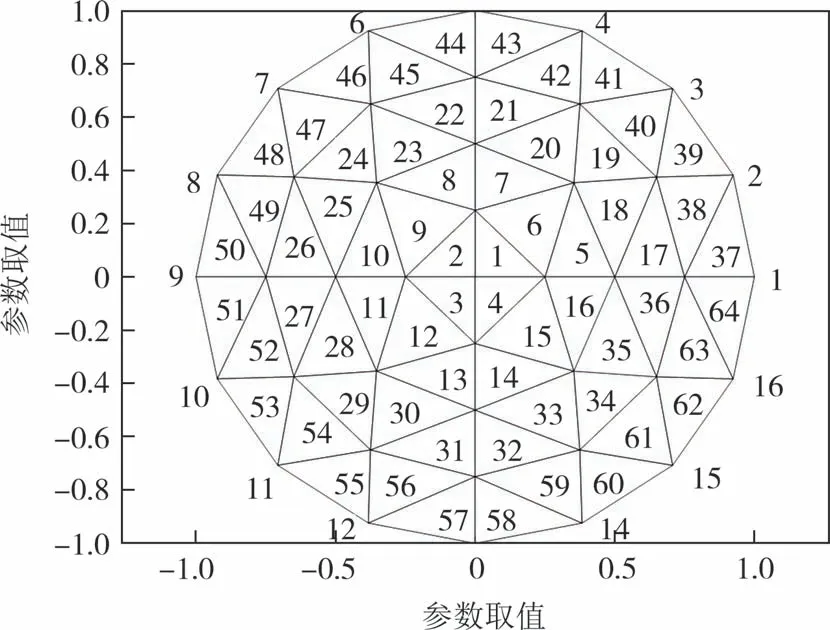
图2 高维参数模型Fig.2 High dimensional parameter model.
为了提高有限元模型的计算效率,我们采用BP神经网络模型作为有限元的替代模型.首先将有限元模型的电阻率值作为网络的输入,计算出的电极电位结果作为网络的输出,随机生成1 000组输入输出数据,选择数据的70%作为网络的训练数据、15%作为修正数据、15%作为测试数据,训练BP 人工神经网络.
利用均方差来度量BP 神经网络的性能,均方误差MSE的计算公式为
式中,N为样本个数,Yi为验证集输出结果,yi为测试集输出结果.图3 显示了BP 神经网络训练过程中的均方差变化.

图3 BP神经网络均方差Fig.3 BP neural network variance diagram.
由图3 可以看出各个测试集最终都趋于收敛,且在迭代完成时四层同心圆模型的均方差低于10-8,高维参数模型的均方差低于10-5,可见BP 神经网络拟合得很好.
进一步对训练好的网络进行验证,按均值±30%随机生成20 组四层电阻率值,分别代入有限元模型以及BP 神经网络模型.计算16 个电极20 组数据的平均相对误差值,如图4 所示,由于9 号电极为参考电极,图中忽略不计.
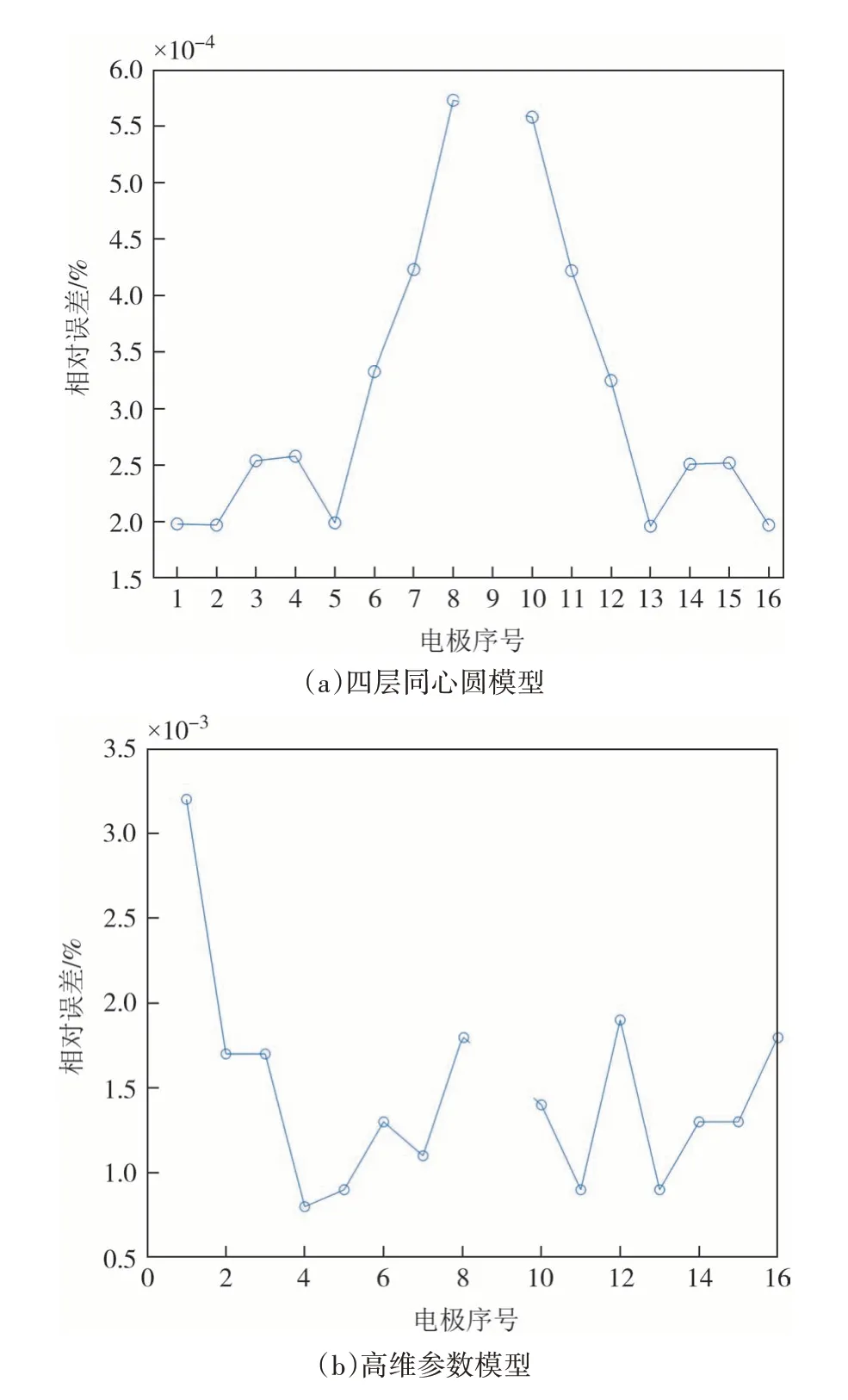
图4 平均相对误差Fig.4 Average relative error.
由图4 可以看出,在四层同心圆模型中BP 神经网络模型与有限元模型的误差在10-5左右,二维圆模型中误差为10-3,说明两种计算模型拟合得很好.在程序运行中,生成1 000 组输入数据,四层同心圆模型用时116.446 s,BP 神经网络用时3.281 s;高维参数模型用时56 875.324 s,BP 神经网络用时389.732 s,说明使用BP 神经网络替代模型极大地提升了计算速度.故BP 神经网络可以作为有限元的替代模型进行后续的参数反演工作.
3 参数反演结果
3.1 基于同心圆模型的低维参数反演
针对同心圆模型进行参数反演,取四层电阻率的先验分布为均匀分布,变化范围取均值的±30%,如表1所示,并假设噪声服从独立的正态分布N(0,22).分别选取相邻激励、相对激励以及间隔六电极激励三种电流激励方式,来探讨不同的激励方式对电阻率反演结果的影响.其中,在相邻激励方式下电流从1号电极注入,2 号电极流出;在相对激励方式下电流从1 号电极注入,9 号电极流出;在间隔六电极方式下电流从1 号电极注入,8 号电极流出.利用DREAM_ZS 抽样算法进行抽样,其中DREAM_ZS 算法的参数设置为:马尔科夫链并行运行的数量为3条,生成候选点的链对数量为1 对,使用3%的交叉值.三种激励方式下电阻率的后验均值以及与真值之间的误差如表2所示.
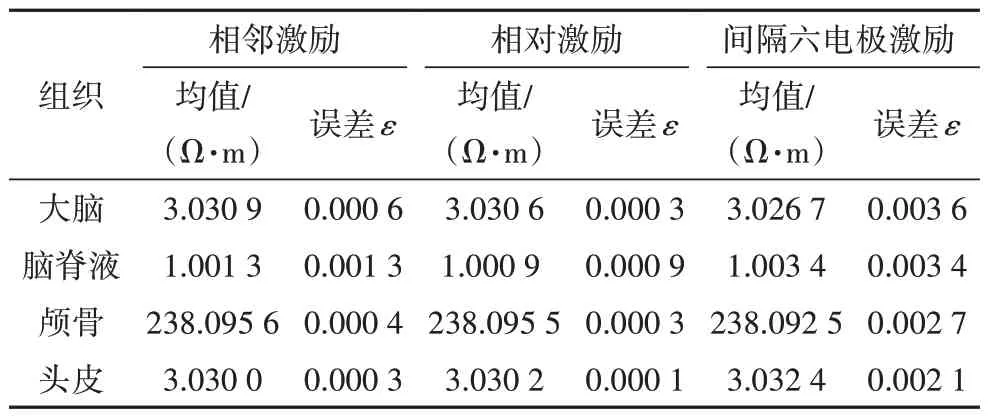
表2 各激励方式下参数后验分布统计信息表Tab.2 Statistical information table of posterior distribution of parameters under various excitation modes
由表2 可知,每层电阻率的后验均值与真值之间的误差很小,说明DREAM_ZS 算法可以识别各个参数.对比不同的激励方式,当电流激励方式为相对激励时误差最小,其次是相邻激励,而间隔六电极激励方式的误差较其它两种方式大很多,这说明在相对激励方式下参数反演效果是最优的,而相隔六电极激励不太理想.在三种激励方式下,头皮的误差均为最小,说明头皮的不确定性最小.在相对激励和相邻激励方式下,颅骨和大脑的误差次之,误差最大的是脑脊液;在间隔六电极激励方式下,颅骨的误差次之,大脑和脑脊液的误差较大.
为了进一步对后验分布的概率值进行衡量,我们引入最大后验概率(Maximum a Posteriori,MAP)值.MAP 是理论上后验分布概率取最大时的参数值,可以判定算法对参数的识别程度.参数的后验分布峰值越接近于MAP,说明对算法的识别效果越好.
三种电流激励方式下的电阻率参数后验分布的边缘概率密度曲线如图5 所示,图中蓝色叉点为MAP值.

图5 各激励方式下参数后验分布边缘概率密度曲线Fig.5 Marginal density curve of posterior distribution of parameters under various excitation modes
通过图5 可以直观地看出:间隔六电极激励方式下,四层电阻率参数后验分布均未出现单个峰值的正态分布形状;相邻激励方式下,头皮和颅骨有近似的单个峰值的正态分布形状;相对激励方式下,头皮、颅骨和脑脊液均有近似的单个峰值的正态分布形状。在反演效果最佳的相对激励方式下,头皮和颅骨的峰值明显,且接近MAP,脑脊液次之,而大脑的整体趋势较为平缓,且峰值离MAP 较远,说明DREAM_ZS 算法对头皮、颅骨的识别能力强,其不确定性小,脑脊液和大脑的不确定性要大.
为了定量描述参数的后验分布信息,计算各激励方式下标准差.其中标准差计算为
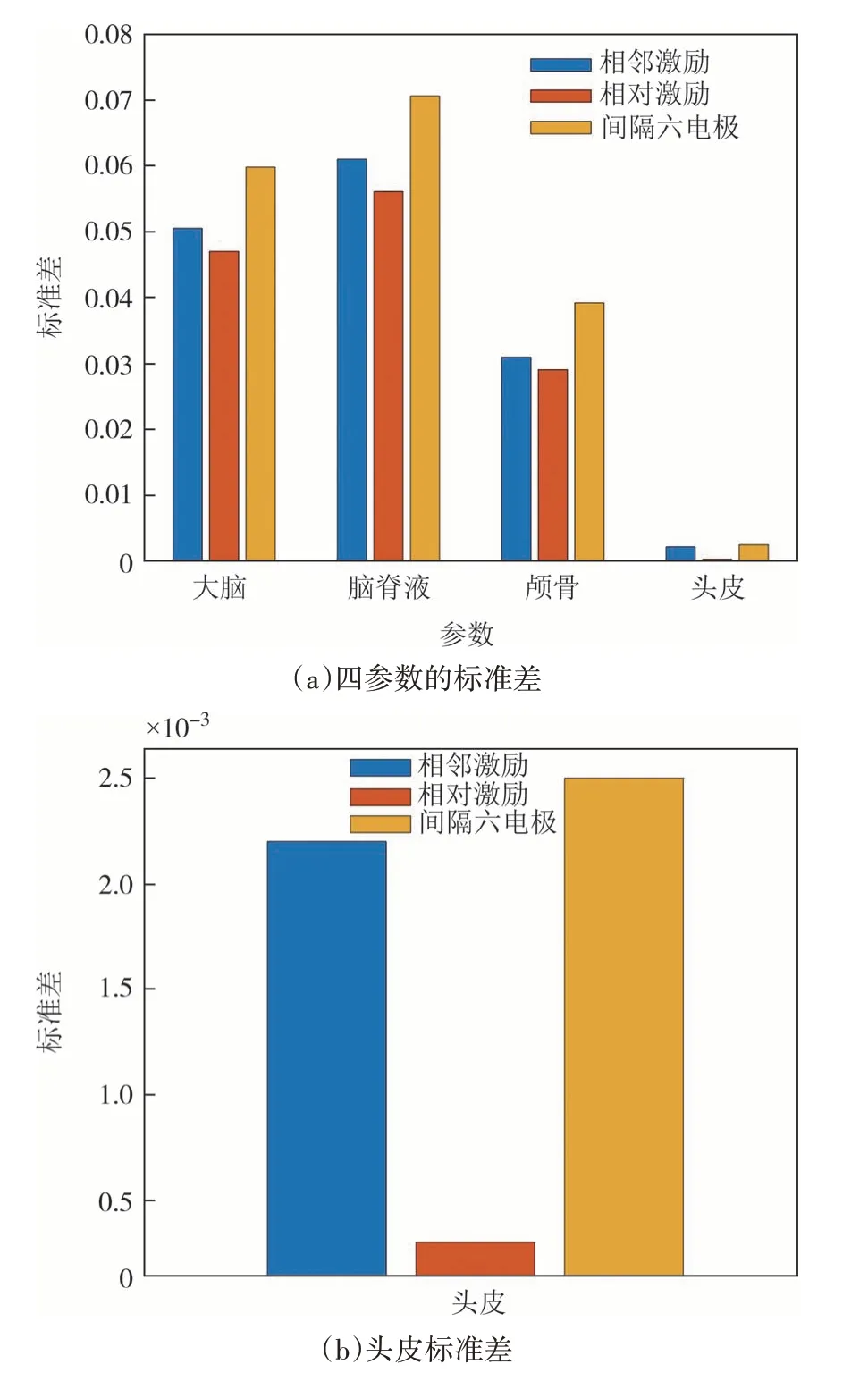
图6 不同激励方式下参数的标准差Fig.6 Standard deviation of parameters under different excitation modes
从图6 可以看出,对于三种激励模式,头皮的标准差均最小,其次是颅骨,而大脑和脑脊液的标准差大一些.说明四个参数中头皮的后验分布最集中,不确定性最小,敏感性最强.其次是颅骨,大脑和脑脊液的不确定性较大.
3.2 基于二维圆模型的高维参数反演
通过前面的结论可以得知在相对激励方式下对逆问题电阻率反演效果最好,所以在高维参数反演中电流采用相对激励方式注入.根据贝叶斯理论可知,先验分布的不同在一定程度上会影响后验结果的分布,所以接下来研究电阻率在不同先验分布下(即均匀分布与正态分布下)参数的反演结果.
3.2.1 先验为均匀分布时参数的反演结果
在对高维参数模型进行的仿真实验中,假设非病灶单元均值为1 Ω·m,而病灶单元电阻率为非病灶单元的2 倍.假设病灶单元和非病灶单元均服从变化范围为均值±20%的均匀分布,即非病灶单元参数服从(0.8,1.2)上的均匀分布,病灶单元参数均服从(1.6,2.4)上的均匀分布.如图7(a)所示,选取9号、10 号、25 号参数区域作为病灶单元进行参数反演.采用DREAM_ZS算法进行抽样,可以得到所有单元的反演结果。各单元先验分布和后验分布的均值结果如图7(b)、图7(c)所示.

图7 先验为均匀分布时的反演结果示意图Fig.7 Schematic diagram of inversion results when prior distribution is uniform distribution
由图7 可知,各单元先验分布和后验分布的均值相差不大,经算法识别后的单元均值接近于真值,说明DREAM_ZS算法可以识别出各个单元参数.
图8 显示了单元9、单元10、单元25 的后验分布边缘密度曲线.对于非病灶单元,由于单元数目过多,我们选取几个典型单元的后验分布边缘密度曲线展示于图9中.

图8 病灶单元后验分布边缘密度曲线Fig.8 Marginal density curve of posterior distribution of parameters when prior is uniform distribution.
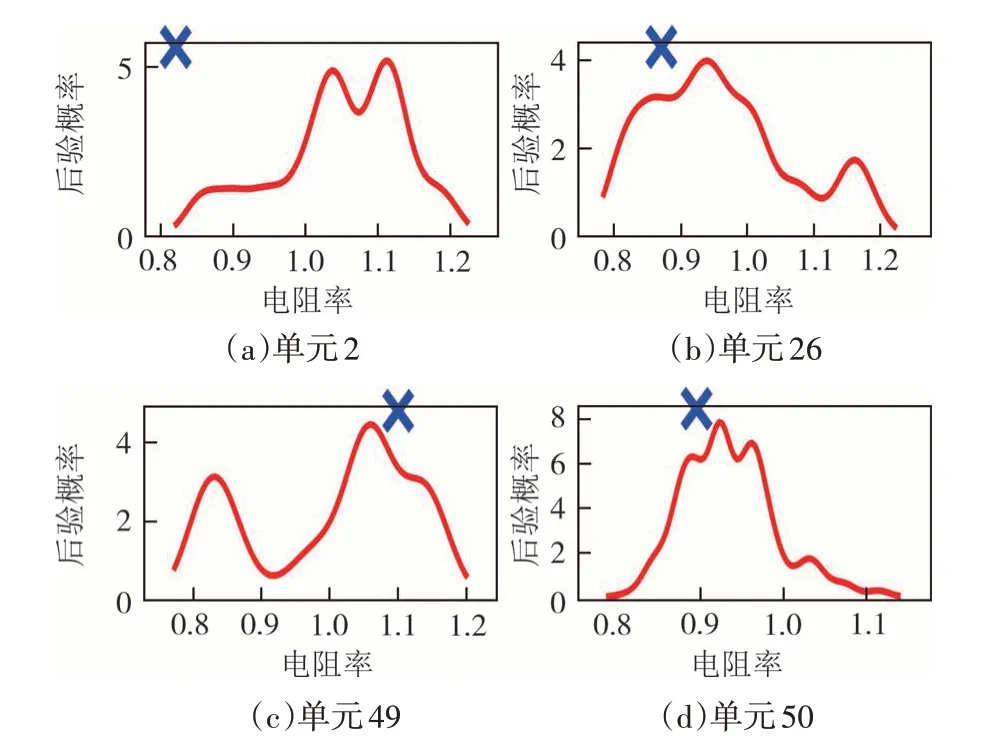
图9 典型单元后验分布边缘密度曲线Fig.9 Marginal density curve of posterior distribution of typical unit
由图8 的曲线趋势可以看出,单元10 的后验分布峰值最接近于MAP,其次是单元9,单元25的峰值与MAP相差最大.说明DREAM_ZS算法对单元10的识别效果更强,对单元9 也可有效识别对单元25 的识别效果较差.单元10 的不确定性要小于单元9 和单元25,敏感性最强.
在图9 中,单元49 和单元50 的峰值最接近于MAP,其次是单元26,单元2 的峰值与MAP 相差最大.说明DREAM_ZS算法对单元49和单元50的识别效果最强,单元26也可以有效地识别出来,单元2的识别效果最差.单元49 和单元50 的不确定性最小,单元2的不确定性最大.
3.2.2 先验为正态分布时参数的反演结果
采用与以上均匀分布相同的高维参数模型.假设病灶单元参数服从均值为2 Ω·m,标准差为0.05的正态分布,其余参数均服从均值为1 Ω·m,标准差为0.05 的正态分布.选取9 号、10 号、25 号参数区域作为病灶单元进行参数反演.各单元先验分布和后验分布的均值结果如图10所示.
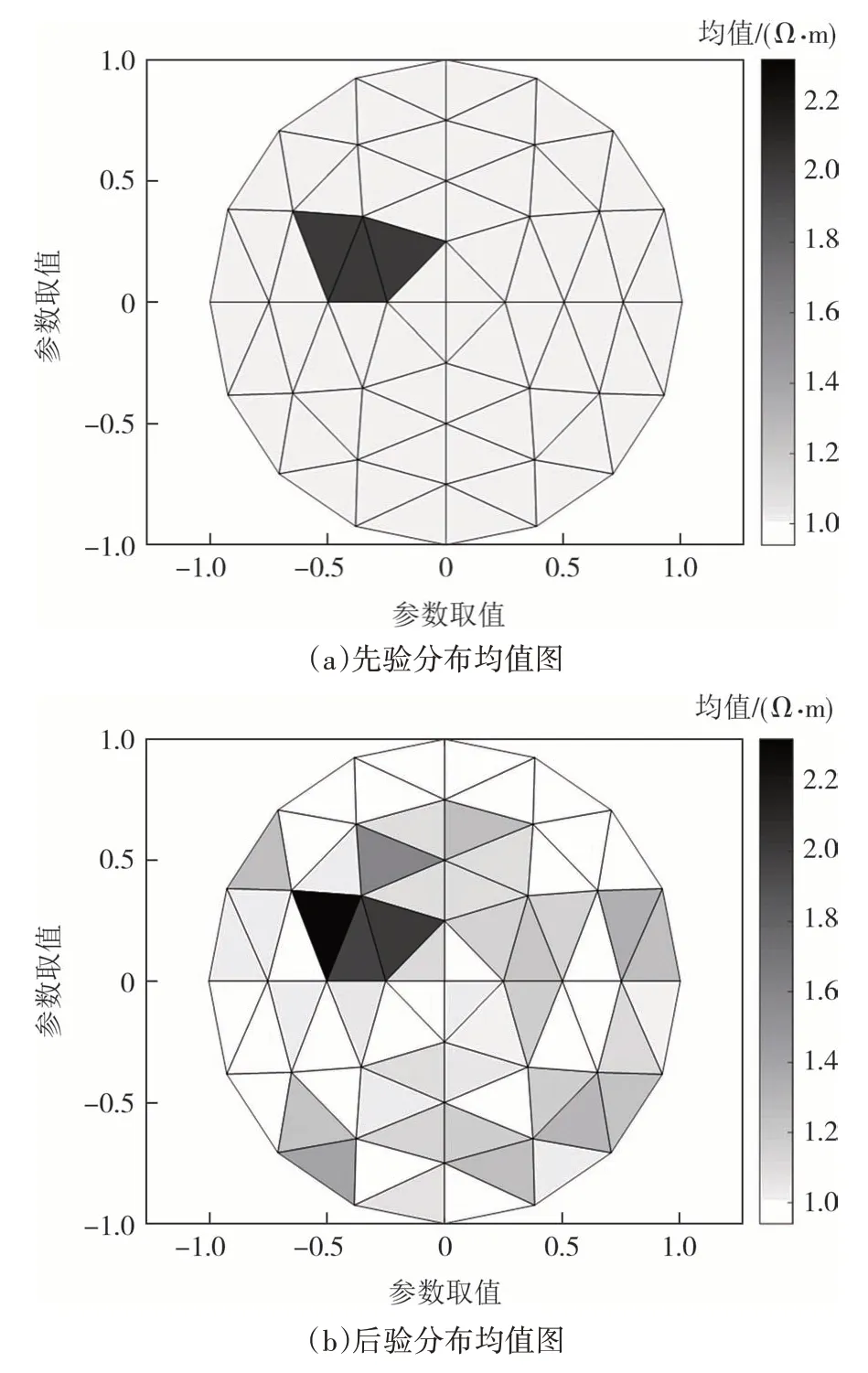
图10 先验分布为正态分布时的反演结果示意图Fig.10 Schematic diagram of inversion results when prior distribution is normal distribution
由图10 可知,各单元先验分布和后验分布的均值相差不大,经算法识别后的单元均值接近于真值,说明DREAM_ZS算法可以识别出各个单元参数.
部分反演结果如图11、图12 所示.由图8、图9、图11、图12 的曲线趋势可以看出:参数的变化波动在先验为正态分布时比为均匀分布时要小,曲线更为规律,更接近于正态分布,而且各参数的峰值离MAP 值更近.说明参数的先验分布为正态时要比为均匀时识别效果更好.
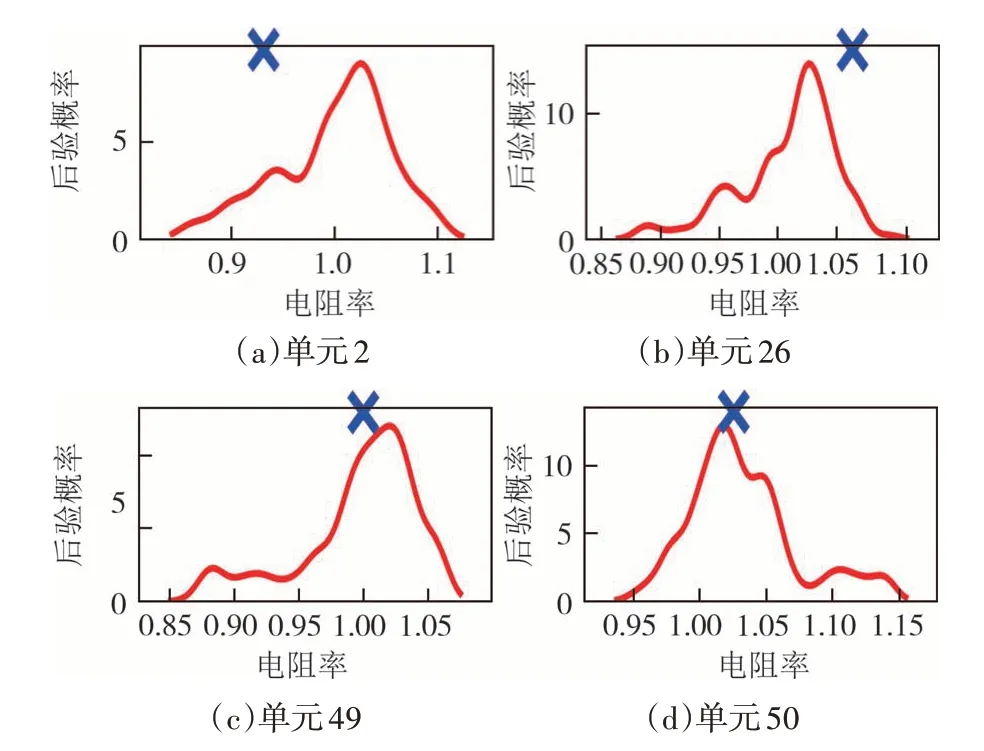
图12 典型单元后验分布边缘密度曲线Fig.12 Marginal density curve of posterior distribution of typical unit
在图11 中,单元25 的后验分布峰值最接近于MAP,其次是单元10 和单元9.说明DREAM_ZS 算法对单元25 的识别效果更强,对单元9 和单元10 的识别效果次之.单元9 和单元10 的不确定性要大于单元25,敏感程度低.在图12 中,单元49 和单元50 的峰值最接近于MAP,其次是单元26,单元2 的峰值与MAP相差最大.说明DREAM_ZS 算法对单元49和单元50的识别效果最强,单元26也可以有效地识别出来,单元2 的识别效果最差.单元49 和单元50 的不确定性最小,单元2 的不确定性最大.
为了更直观地说明参数的后验标准差分布,作出各单元标准差的灰度图,如图13所示.
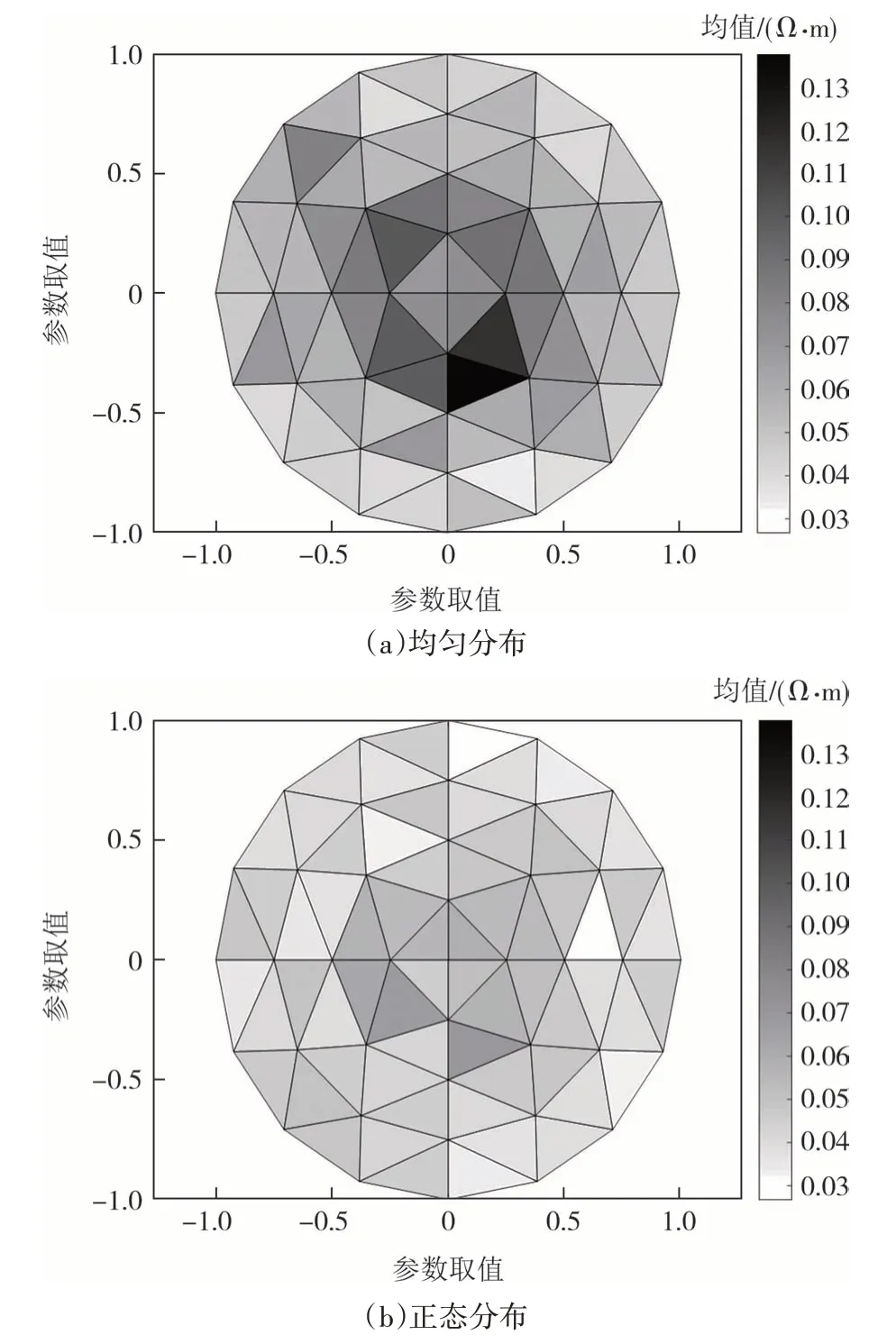
图13 不同先验分布下后验分布标准差灰度图Fig.13 Gray scale of standard deviation of posterior distribution under different prior distributions
由图13 可以直观地看出:不论先验是均匀分布还是正态分布,内层16 个单元的标准差均大于外层标准差.这说明圆模型的内层参数的不确定性要大于外层.分析可知,这是由于外层参数单元距离电极更近,对电极的变化也就更敏感.前16 个单元后验分布的标准差都要大于先验的标准差,其余单元后验分布的标准差都小于先验的标准差,这说明这些单元的后验分布相对于先验分布变得集中,参数经DREAM_ZS算法识别降低了不确定性.
4 结论
1)利用BP 神经网络模型替代有限元模型完成EIT 正问题的计算,取得了计算精度高的结果,且大大提高计算效率,为EIT参数反演打下基础.
2)对于EIT 低维反演问题,基于四层同心圆模型,在贝叶斯框架下,采用DREAM_ZS 抽样算法,对四个参数进行了有效地反演,并分析了各个参数的不确定性,发现头皮的不确定性最小,其次是颅骨,大脑和脑脊液的不确定性较大.对比不同的电流激励模式发现,相对激励的参数反演效果最优.
3)以二维圆模型为仿真算例研究EIT 高维反演问题,基于贝叶斯框架的DREAM_ZS 抽样算法能够准确识别病灶单元.对比不同的先验分布,发现正态分布比均匀分布的反演结果更优.另外,单元与电极的相对位置会影响其反演结果和不确定性.当先验为正态分布时,单元距离电极越近,其参数不确定性越小,算法识别程度越高.
4)基于贝叶斯理论的参数反演方法在EIT 不确定性量化研究中具有可靠性高、适用范围广的优点.在已知参数不确定性程度的基础上,如何合理地给出改进不确定性较大参数的方法,这需要在今后的研究中做进一步探索.

