基于中心差商的一类避免求导的非线性方程迭代算法

郭巧 杨兵 王伟昌

【摘   要】   非线性方程求解的迭代方法中比较经典的牛顿迭代法、改进牛顿法等，虽然能够提高迭代效率，但因为需要对非线性方程求导并要求导数不能为零，使得其在实际应用中具有一定的局限性。文章基于开依沙尔·热合曼等人提出的四阶收敛迭代格式，利用中心差商近似代替一阶导数，通过对加权因子进行赋值，得到一类避免求导的四阶收敛的迭代算法。收敛性分析和数值实例证明该方法适用于大多数非线性方程的求根问题，在工程计算方面具有一定的实用价值。

【关键词】   中心差商；非线性方程；避免求导；四阶收敛

A Class of Iterative Algorithms for Nonlinear Equations Without Derivation Based on Central Difference

Guo Qiao1， Yang Bing1， Wang Weichang2

（1.Anhui Vocational and Technical College， Hefei 230611， China;

2.Anhui Gongbu Zhizao Industrial Technology Co.， Ltd.， Hefei 238000， China）

【Abstract】    The classical iterative methods for solving nonlinear equations， such as Newton′s iterative method and improved Newton′s method， can improve the efficiency of iteration but have limitations in practical applications because they require derivatives of nonlinear equations and the derivatives cannot be zero. Based on the fourth-order convergent iterative format proposed by Kaishal-Rehman et al， the article obtains a class of fourth-order convergent iterative algorithms that can avoid derivatives by using the central difference quotient approximation instead of the first-order derivatives and assigning weighting factors. convergence analysis and numerical examples demonstrates that the methods should be applied to most nonlinear equation in finding root problems， and that they have a certain practical value in engineering calculation.

【Key words】     central difference quotient; nonlinear equations; avoiding derivative; fourth-order convergence

〔中图分类号〕  O241.3                 〔文献标识码〕  A              〔文章编号〕 1674 - 3229（2024）01- 0018 - 05

0     引言

非线性方程求根问题作为计算数学的一个重要分支，其广泛应用于非线性轨迹优化、分数阶时滞控制等各种工程计算领域，能够有效实现路径精准定位并控制指令滞后，在流体力学、半导体、现代光学、高层建筑、石油勘探、天气预报等方面具有重要的应用价值和研究意义，比较经典的求非线性方程单根的方法为牛顿迭代［1］：

[xn+1=xn-f（xn）f'（xn），n=0，1，2…] （1）

在此基础上，Traub引入算术平均牛顿法（AN）［2］，收敛阶数为三阶，迭代算式为：

[yn=xn-f（xn）f′（xn），xn+1=xn-2f（xn）f′（xn）+f′（yn），n=0，1，2，…]        （2）

黄象鼎等提出调和平均牛顿法（HN）和中点牛顿法（MN）［3］，收敛阶数为三阶，迭代算式为：

[yn=xn-f（xn）f′（xn），xn+1=xn-f（xn）（f′（xn）+f′（yn）2f′（xn）f′（yn），n=0，1，2，…] （3）

[yn=xn-f（xn）f′（xn），xn+1=xn-f（xn）f′（xn+yn2），n=0，1，2，…]                 （4）

上述迭代算法及其變形虽然能够提高迭代收敛阶并减少计算量，但是却无法避免求导。对于复杂的函数类型，利用现有的知识储备往往难以求出其导数或者所求函数导数为零，这两种情况限制了迭代算法适用的函数类型。文章基于导数的几何意义，利用中心差商的方法，提出了一类避免求导的迭代算法，该算法适用于所有需要求导或者导数为零的迭代情况，能够有效扩大迭代算法适用的函数范围，收敛性分析和数值实例进一步验证了该算法不仅收敛速度更快而且能够有效避免重根附近发散，在非线性方程求根领域具有更广泛的适用性和研究意义。

1     预备知识

定义1［4］     设非线性方程[f（x）=0]的解为[α]，如果迭代序列[xn（n=1，2，3，…）]满足[limn→∝xn=α]，则迭代序列[xn（n=1，2，3，…）]收敛于[α]。

定义2［5］    设非线性方程[f（x）=0]的精确解为[α]，迭代序列为[xn（n=1，2，3，…）]，记[en=xn-α]为迭代误差，若存在常数C及[p]，使得[en+1=Cepn+O（ep+1n），] 称迭代序列为[p]阶收敛。

定义3［6］    设函数[y=f（x）]在点[x0]的某邻域内有定义，若

[limΔx→0ΔyΔx=limΔx→0f（x+Δx）-f（x）Δx] 存在，则称函数[y=f（x）]在点[x0]可导，此极限为[y=f（x）]在点[x0]的导数，记作：[f′（x0）]。

2     迭代算法

下面所写的迭代算式中，统一记[n=0，1，2，3，…。]根据定义3，得到

[f′（xn）=limf（xn）→0f（xn+f（xn））-f（xn）f（xn）≈f（xn+f（xn））-f（xn）f（xn）]       （5）

[f′（xn）=limf（xn）→0f（xn）-f（xn-f（xn））f（xn）≈f（xn）-f（xn-f（xn））f（xn）]       （6）

公式（5）和公式（6）利用一阶导数的中心差商计算，近似得

[f′（xn）≈f（xn+f（xn））-f（xn-f（xn））2f（xn）]              （7）

文献［7］中的迭代算法为：

[xn+1=xn-ωf（xn）+f（x*n+1）f′（xn）-（1-ω）f（xn）+2f（x*n+1）f（xn）+f（x*n+1）f（xn）f′（xn）x*n+1=xn-f（xn）f′（xn）]      （8）

將公式（7）代入公式（8），得到如下迭代算式：

[xn+1=xn-ω2f2（xn）+2f（xn）f（x*n+1）f（xn+f（xn））-f（xn-f（xn））-（1-ω）f（xn）+2f（x*n+1）f（xn）+f（x*n+1）2f2（xn）f（xn+f（xn））-f（xn-f（xn））x*n+1=xn-2f2（xn）f（xn+f（xn））-f（xn-f（xn））]    （9）

公式（9）即为本文迭代算法。在权系数[ω=97]时，文献［7］定义的迭代算式表示为：

[xn+1=xn-97f（xn）+f（x*n+1）f′（xn）+27f（xn）+2f（x*n+1）f（xn）+f（x*n+1）f（xn）f′（xn）x*n+1=xn-f（xn）f′（xn）]       （10）

公式（9）定义的迭代算式表示为：

[xn+1=xn-972f2（xn）+2f（xn）f（x*n+1）f（xn+f（xn））-f（xn-f（xn））+27f（xn）+2f（x*n+1）f（xn）+f（x*n+1）2f2（xn）f（xn+f（xn））-f（xn-f（xn））x*n+1=xn-2f2（xn）f（xn+f（xn））-f（xn-f（xn））]   （11）

3     收敛性分析

定理1   如果[α∈I]是函数[f：I?R→R]在开区间[I]上的一个单根，函数[f（x）]在[I]上连续可导（一阶到四阶导数都存在），在[α]的邻域内给定初始值[x0]，则公式（9）定义的迭代算法误差方程表示为：

[en+1=（-7ωc22c21+9c22c21）e3n+1c31（33ω-42）c32+（10-13ω）c21c4+（10ω-3）c1c2c3+（4-ω）c31c2c3+（4-4ω）c41c4+（ω-1）c21c2c3+（4-4ω）c31c4+（5-5ω）c32c1e4n+O（e5n）]  （12）

其中[en=xn-α， ci=fi（α）i！，i≥1]。

证明：函数[f（x）]在[α]处进行Taylor展开，得

[f（xn）=c1en+c2e2n+c3e3n+c4e4n+O（e5n）]             （13）

于是

[2f2（xn）=2c21e2n+4c1c2e3n+（2c22+4c1c3）e4n+（4c1c4+4c2c3）e5n+O（e6n）]     （14）

[f（xn+f（xn））-f（xn-f（xn））=i=1∝ci[（en+f（xn））i-（en-f（xn））i]=2c21en+6c1c2e2n+（8c1c3+2c31c3+4c22）e3n+（10c1c4+10c2c3+6c21c2c3+8c31c4）e4n+O（e5n）] （15）

由公式（14）、公式（15）可知

[2f2（xn）f（xn+f（xn））-f（xn-f（xn））=en-c2c1e2n+2c22c21-2c3c1-c1c3e3n+-6c4c1+7c2c3c21+c2c3-4c1c4-4c32c31e4n+O（e5n）] （16）

将公式（16）代入（12）得

[x*n+1=α+c2c1e2n+2c3c1+c1c3-2c22c21e3n+6c4c1-7c2c3c21-c2c3+4c1c4+4c32c31e4n+O（e5n）]           （17）

[f（x*n+1）=c2e2n+2c3+c21c3-2c22c1e3n+6c4-7c2c3c1-c1c2c3+4c21c4+5c32c21e4n+O（e5n）]            （18）

由公式（13）、公式（18）可知

[2f（xn）f（x*n+1）=2c1c2e3n+2（c22+2c1c3+c31c3-2c22）e4n+（-8c2c3+6c32c1+12c1c4+8c31c4）e5n+O（e6n）]           （19）

由公式（14）、公式（19）有

[2f2（xn）+2f（xn）f（x*n+1）=2c21e2n+6c1c2e3n+（8c1c3+2c31c3）e4n+（-4c2c3+6c32c1+16c1c4+8c31c4）e5n+O（e6n）]     （20）

由公式（15）、公式（20）得

[2f2（xn）+2f（xn）f（x*n+1）f（xn+f（xn））-f（xn-f（xn））=en-2c22c21e3n+9c32c31+3c4c1-7c2c3c21-3c2c3e4n+O（e5n）.]             （21）

由公式（13）、公式（14）、公式（18）得

[f（xn）+2f（x*n+1）=c1en+3c2e2n+5c3+2c21c3-4c22c1e3n+O（e4n）]       （22）

[（f（xn）+2f（x*n+1））?2f2（xn）=2c31e3n+10c21c2e4n+14c21c3-6c1c22+4c41c3e5n+4c21c4+36c1c2c3-10c32+8c31c2c3e6n+O（e7n）]   （23）

[f（xn）+f（x*n+1）=c1en+2c2e2n+3c3+c21c3-2c22c1e3n+7c4-7c2c3c1-c1c2c3+4c21c4+5c32c21e4n+O（e5n）.]      （24）

由公式（15）、公式（24）得

[f（xn）+f（x*n+1）f（xn+f（xn））-f（xn-f（xn））=2c31e2n+10c21c2e3n+14c21c3+4c41c3+12c1c22e4n+24c21c4+30c1c2c3+16c31c2c3+8c41c4-4c32-2c21c2c3+8c31c4+10c32c1e5n+O（e6n）                                                                                                （25）]

由公式（23）、公式（25）得

[f（xn）+2f（x*n+1）?2f2（xn）f（xn）+f（x*n+1）f（xn+f（xn））-f（xn-f（xn））=en-9c22c21e3n+1c3142c32-10c21c4+3c1c2c3-4c31c2c3-4c41c4+c21c2c3-4c31c4-5c32c1e4n+O（e5n）                                      （26）]         將公式（21）、公式（26）代入公式（9），于是得

[en+1=-7ωc22c21+9c22c21e3n+1c31（33ω-42）c32+（10-13ω）c21c4+（10ω-3）c1c2c3+（4-ω）c31c2c3+（4-4ω）c41c4+（ω-1）c21c2c3+（4-4ω）c31c4+（5-5ω）c32c1e4n+O（e5n）]

定理1得证。

当[ω=97]时，公式（9）定义的迭代算法误差方程表示为

[en+1=3c327c31-47c47c1+69c2c37c21+197c2c3-8c1c47+2c2c37c1-8c47-10c327c41e4n+O（e5n）]

4     数值实例

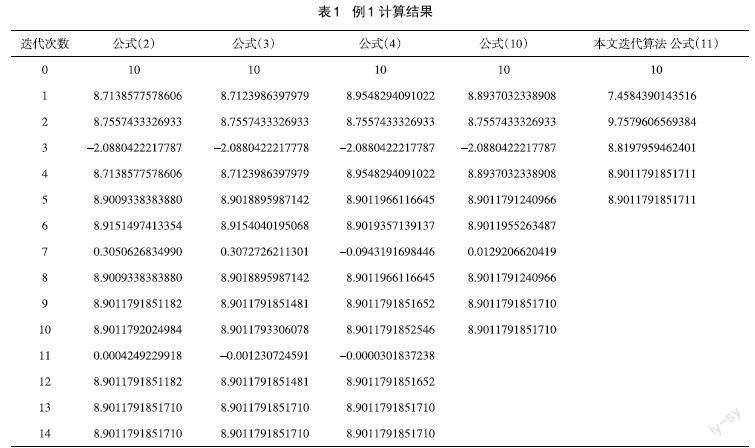
例1   求方程[f（x）=x3-ex-3x+2=0]的根，取初始值[x0=10]。反复利用公式（2）、公式（3）、公式（4）、公式（10）和本文迭代算法（公式（11），令[xn-xn+1≤10-13]时迭代终止，在Python语言环境下，计算结果如表1所示。

通过例1，在函数类型、初始值、计算环境相同的情况下，公式（2）、公式（3）、公式（4）需要进行14次迭代（其中经历3次发散）达到精度要求，公式（10）需要进行10次迭代（其中经历2次发散）达到精度要求，但是本文迭代算法只需要进行5次迭代经历0次发散就可以达到精度要求。由此证明本文迭代算法远优于三阶以及四阶收敛速度的Newton迭代算法的变型形式，并且能够有效控制重根附近发散，对于非线性方程求根中函数类型难以求导和导数不存在的情况都有较好的适用效果，在非线性轨迹优化、分数阶时滞控制等工程计算领域具有重要的研究意义。

［参考文献］

［1］  管慧莹. 求解非线性方程的两种迭代算法［D］.哈尔滨：哈尔滨理工大学，2020.

［2］ Muhammed K S， Krishnendu R， Santhosh G， et al.Local Convergence of Traub′s Method and Its Extensions［J］.Fractal and Fractional，2023，7（1）：98.

［3］  黃象鼎，曾钟钢，马亚南.非线性数值分析的理论与方法［M］.武汉：武汉大学出版社，2004.

［4］ 范倩楠，王晓锋.求解非线性方程的4阶收敛的无导数迭代法［J］.哈尔滨师范大学自然科学学报，2020，36（4）：1-4.

［5］ Vanhille Christian. A note on the convergence of the irrational Halleys iterative algorithm for solving nonlinear equations［J］. International Journal of Computer Mathematics，2020，97（9）：235-246.

［6］  谭俊键，杨敏.调和映射的Schwarz导数与对数导数的新定义及其范数［J］.贵州师范大学学报（自然科学版），2022，40（3）：13-17.

［7］  开依沙尔·热合曼，热合买提江·依明江，买买提明·艾尼.求解非线性方程根四阶收敛的迭代格式［J］.数学的实践与认识，2013，43（7）：236-240.