质量图引导的干涉合成孔径雷达图像相位解缠算法

郝红星， 于荣欢， 张喜涛

(1. 装备学院 复杂电子系统仿真实验室, 北京 101416； 2. 装备学院 研究生管理大队, 北京 101416)

质量图引导的干涉合成孔径雷达图像相位解缠算法

郝红星1， 于荣欢1， 张喜涛2

(1. 装备学院 复杂电子系统仿真实验室, 北京 101416； 2. 装备学院 研究生管理大队, 北京 101416)

干涉合成孔径雷达测量在数字高程数据获取等遥感领域得到广泛应用，相位解缠是干涉测量中的关键步骤。运用基于质量图的马尔科夫随机场建模方法将相位解缠问题转化为能量最小化问题，通过序列树权值信息传递算法对所建立的马尔科夫随机场模型进行求解。论文提出通过最小方向线性插值方法对相位图像中质量较差的区域进行修复，即根据质量较差的像素点所处的位置，利用最短的方向对质量差的像素点进行插值修复，以获得完整的解缠结果。实验结果表明：相对于不采用质量图的方法以及Goldstein枝切法等解缠算法，所提出的算法能够完成复杂真实地形对应的相位图像解缠。

遥感信息；干涉合成孔径雷达；相位解缠；数字高程模型；马尔科夫随机场

干涉合成孔径雷达(InSAR)测量,已经广泛应用于地形高程数据快速测量、沉降分析、海洋监测等。在军事应用中，干涉合成孔径雷达获得的相位图像相对于其他测量方式，能够比较快速完成地形高程数据的测量。美国于21世纪初利用干涉测量方法开始了全球数字高程数据测量，“奋进号”航天飞机上的SRTM(Shuttle Radar Topography Mission)系统在234 h的全球性作业中获得了地球北纬60°～南纬56°的干涉相位图像，面积超过1.19×109km2[1]。近些年，各国相继发射星载干涉合成孔径雷达用于陆地测图、区域性观测和资源调查等，主要包括德国的TerraSAR-X/TanDEM-X、欧空局的Sentinel-1 A/B、意大利的Cosmo-Skymed星座项目、日本的ALOS/ALOS-2，以及我国的遥感卫星十五号、高分三号。

由于测量机制的局限性，干涉测量获取的相位图像并不能直接使用。通过合成孔径雷达所获取的干涉相位图像由于地表反射率差别，天气状况、电子设备噪声以及前序传输过程的影响，存在大量噪声。这些噪声导致在相位图像中存在残差点(相位不连续的点)，而残差点影响最终的数字高程数据的正确性。另外，获取的相位图像是真实相位(也称为绝对相位)的模2π值，并不能直接应用于高度信息的判读。由于测量数据的这种周期特性，使得相位图像的处理成为非常困难的逆问题。

为了将相位图像处理逆问题转化为可以解决的形式，进而获取能够使用的高程信息，大多数算法将绝对相位(与真实地形高程成比例的相位值)的估计分成2个阶段：第一个阶段，进行干涉相位的估计，即将获得的相位图像进行降噪，获得降噪后的缠绕相位值；第二个阶段，将第一个阶段获取的降噪后的缠绕相位进行绝对相位估计，这一阶段又被称为相位解缠或相位展开，本论文重点关注该阶段的算法研究。

相位解缠是干涉相位图像数据处理过程中的关键步骤。最初的相位解缠算法为多项式曲面建模的方法，例如文献[2]中提出了运用低次多项式曲面近似进行相位解缠的方法。但是在实际的应用中，一个多项式曲面并不能精确地描述整个相位曲面，因此需要将相位平面分割为不同的部分，然后对每一部分运用不同的参数曲面模型进行建模。这种建模方式复杂度较高且解缠效果也不理想。目前，相位解缠算法主要可分为2大类：路径跟随算法和基于最优化的算法。路径跟随算法主要包括Goldstein枝切算法[3-4]、基于置信图的枝切算法[5]、Flynn的最小不连续性算法[6]、路线积分法[7]等。该类算法的主要缺点是容易受到噪声的影响，并且需要满足Itoh条件，即任意2个像素点之间的相位差小于π，但是实际情况中具有非连续区域的相位图像由于条纹相干性比较差，并不能很好地满足该条件。基于最优化的方法主要包括最小p范数相位解缠[8]、最小二乘法算法[9]25和集群智能算法[10]5502等。其中，最小p范数算法并不能很好地保留相位图像中的不连续区域，Guo等[9]25提出通过改进最小二乘法进行相位解缠，能够有效改善解缠精度和解缠速度，但是其解缠过程中忽略了非连续相位导致的相干性较差区域的解缠，因此只能适用于连续平滑相位的解缠过程；Maciel等[10]5504提出基于集群智能的相位解缠算法，但算法实施过程中需要对智能策略进行选择。

现有的相位解缠算法针对连续相位能够取得较好的解缠效果，但是对于真实数据，其解缠效果较差，尤其对于相干性较差区域的干涉相位图像不能正确地进行解缠。本文研究了一种基于质量图和马尔科夫随机场建模的相位解缠算法，有效结合了路径跟随和最优化算法的优势。文献[11]中也研究了基于质量图的马尔科夫随机场模型应用于InSAR图像的处理，但是该文献中将对应模型应用于相位图像的降噪问题，与本论文中解决的相位解缠问题是有区别的。

1 相位解缠问题及其马尔科夫随机场建模

在实际应用中，干涉合成孔径雷达通过获取测量信号的相位差得到测量的相位图像，由于测量信号的周期特性，测量的相位图像并不与实际测量曲面几何对应，而是实际信号的模2π值，即在干涉图像I中，干涉测量相位φ2π(p)与实际相位φ(p)之间的关系满足

φ(p)=φ2π(p)+2k(p)π,∀p∈I

(1)

式中，k(p)为像素点p处的解缠标签值。相位解缠的过程为确定k(p),使其解缠后的相位图像能够满足局部平滑性的特点。对于相位图像φ2π中的相邻像素点p和q，定义平滑性准则Epq(φ(p)-φ(q))为相邻像素点差值绝对值的连续单调增函数，忽略噪声影响，可将相位解缠问题建模为

(2)

式中，(p,q)∈e,标志p和q为相位图像中的相邻像素点，本文中e(马尔科夫随机场图中的边)的确定与质量图有关。公式(2)是马尔科夫随机场的简化形式，根据公式(1)对其进行进一步简化，得到

2π(k(p)-k(q)))

(3)

式中:Z为整数的集合。相位解缠的过程为针对固定像素点p，确定整数值标签k(p),使得式(3)取最小值的过程。

通常情况下，相位解缠问题中的e为相邻像素点，这种方式导致相位图像中的非连续区域在求解最小化过程中被平滑而获得错误的解缠结果。本文将质量图引入马尔科夫随机场模型，在解缠过程中能有效防止相位图像中质量较差的区域误差积累，从而获得正确的绝对相位。e的确定过程如图1所示。

1) 根据质量图Q及设定的阈值η,将质量图进行二值化得到Qb,即

(4)

2) 根据二值化质量图确定马尔科夫随机场模型中边的集合e。若像素p的四邻域对应的Qb都为高质量区域，如图1a)所示，则在马尔科夫随机场模型中考虑其4条边；若像素p的四邻域中有某一方向为质量较差的区域，如图1b)所示，则在马尔科夫随机场中只考虑其3条边；类似，其他2种情况边的建模如图1c)～图1d)所示。

3) 若质量图中出现孤立点，如图1e)所示，则将质量图中该点的质量置为0。

下面对相位解缠对应的马尔科夫随机场最优化问题进行求解。

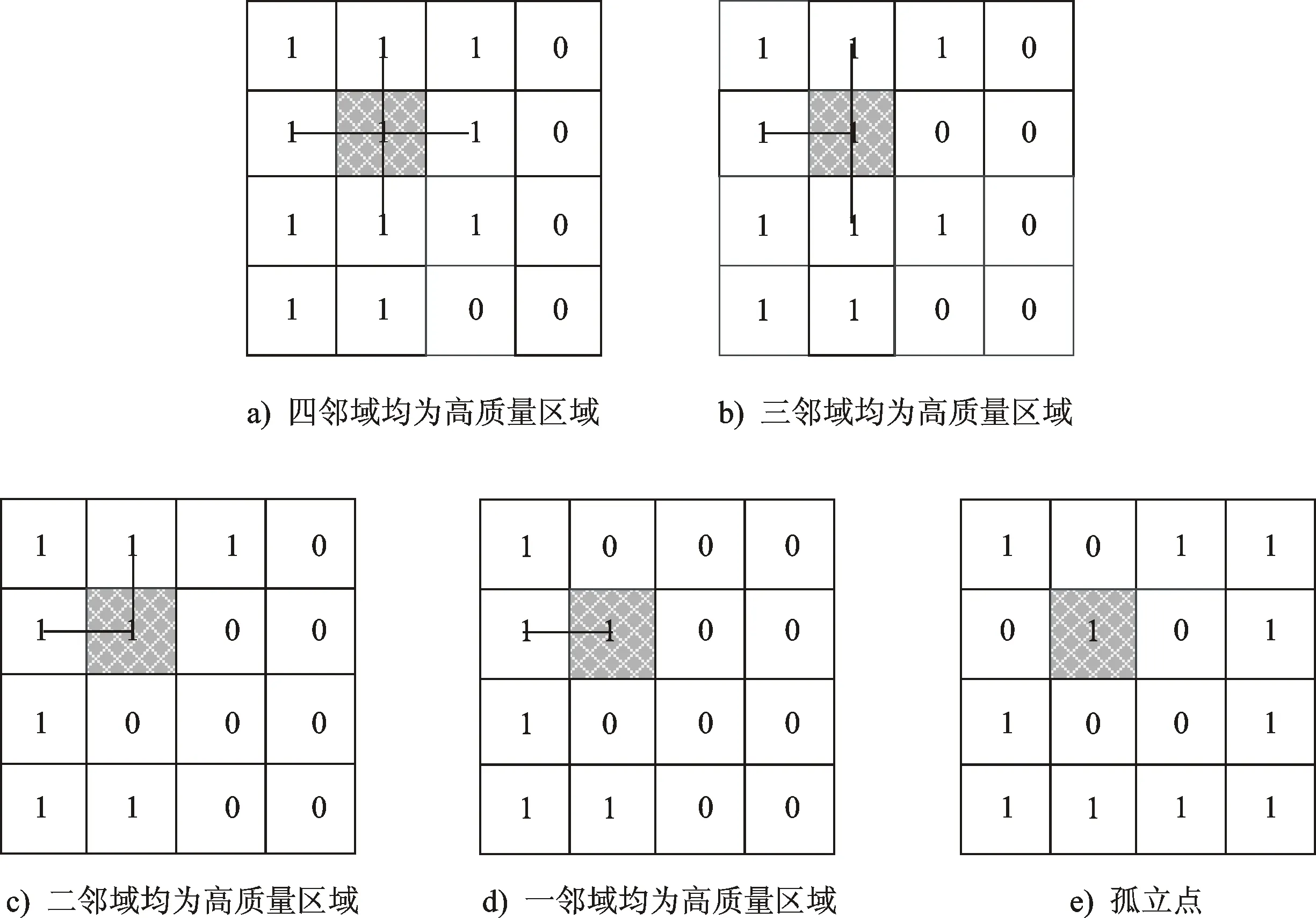
图1 待建模像素周围的二值化质量图情况(阴影像素为待建模像素)

2 马尔科夫随机场问题求解

本文运用序列树权值信息传递算法求解相位解缠问题对应的马尔科夫随机场问题，前文已运用质量图和平滑度相结合的方式对相位解缠问题进行了概述。通过分析可得，所建立的模型是只含有二元项的马尔科夫随机场问题的简化形式，并提出运用信息传递算法求解，其算法步骤为：

第1步：初始化每个顶点的标签值为k(p)=0,传递信息值为Mpq=0,目标函数下界最大值为Elowbound=0；

第2步：进行正向最优化，对于相位图像中的每一个像素点(i,j)，计算该像素点右边和下边2条边的信息传递，即Epq包括像素点(i,j)与(i+1,j)和像素点(i,j)与(i,j+1)2条边对应的二元值。

(5)

式中：st为传递信息值的索引；Mst;l为标签值l对应的传递信息值修正，其定义为Mpq;l-cMn;l(c为修正参数，Mn;l为像素点(i,j)的邻域传递信息值之和)。

第3步：进行逆向最优化，对于相位图像中的每一个像素点(i,j)，计算该像素点左边和上边2条边的信息传递，即Epq包括像素点(i,j)与(i-1,j)和像素点(i,j)与(i,j-1) 2条边对应的二元值,并计算目标函数下界最大值

(6)

第4步：从图像左上角像素点开始，计算每个像素点的标签值k(p),并计算当前目标函数值Eupbound。

第5步：若Eupbound-Elowbound<ε,则终止算法;否则，令Elowbound=0,并转第2步。

若马尔科夫随机场中二元项为凸函数，则上述算法能够收敛于最优解。为了防止一般情况下二元项为非凸时的算法无限迭代，可以设置最大迭代次数Imax。但在相位解缠问题中，由于本文算法通过质量图来避免连续区域的平滑，因此可以设置二元项为凸函数。

3 低质量区域修复算法

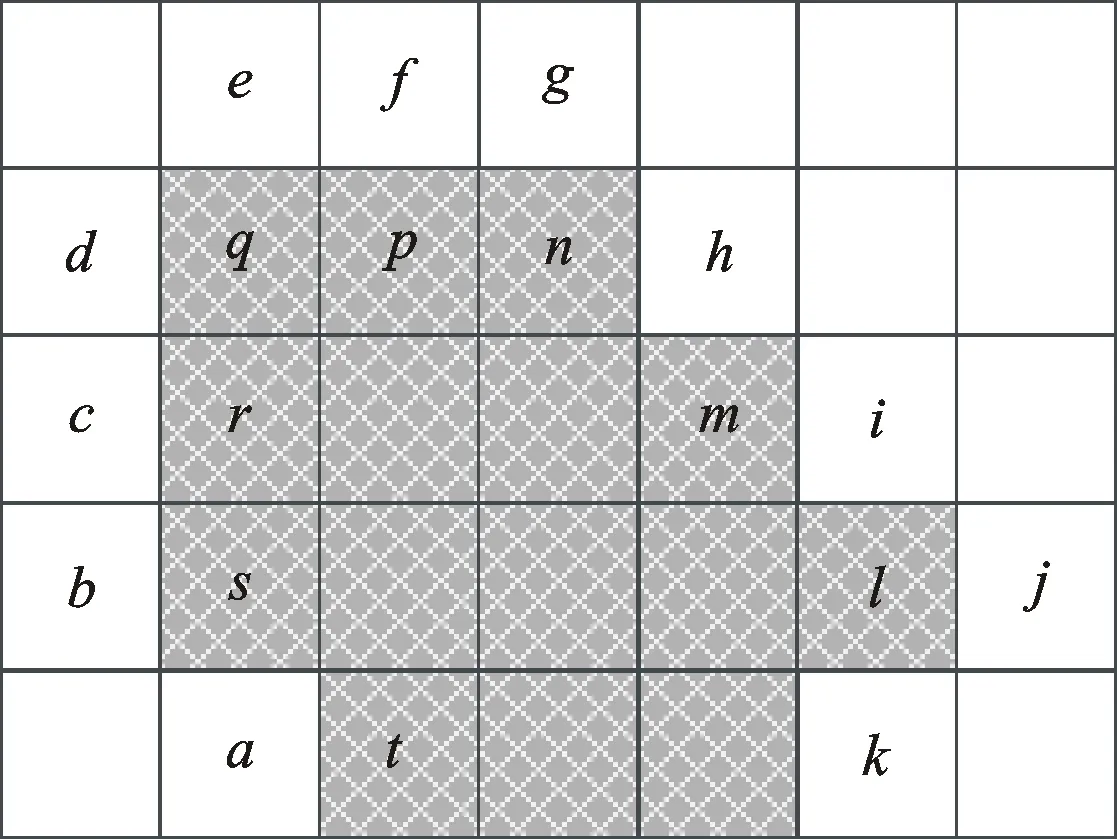
图2 质量低区域修复示意图(阴影区域质量图为0)

通过第2部分算法，对于质量图为1的像素点能够获得正确的标签值，因此可以获得正确的解缠值，从而获得绝对相位。但对于质量图中值0对应的像素点，由于在建模过程中忽略了对应边，因此需要单独考虑。另外，由于质量图中值为0的区域不可用信息较少，因此本文通过最短距离插值方法对该区域进行修复获得绝对相位。根据待修复像素点所处的位置可将修复过程具体分3种情况：

1) 若像素点所在的区域，横向与纵向质量图值为0的像素点个数存在最小值且没有到达图像边缘，则采用在该方向进行线性插值来进行修复。如图2中像素点r，其横向待修复点个数为4，纵向待修复点个数为3，因此其通过纵向进行修复，即φ(r)=L(φ(a),φ(e)),其中L(·)为线性插值函数。

2) 若像素点所在区域，横向与纵向质量图值为0的像素点个数相等且没有到达图像边缘，则采用双线性插值方法进行修复。如图2中像素点q，其横向和纵向待修复点的个数都为3，则通过双线性插值进行修复，即

φ(q)=(L(φ(a),φ(e))+L(φ(d),φ(h)))/2

3) 若像素点所在区域，某一方向质量图为0的像素点到达图像边缘，如图2中像素点m，虽然其纵向待修复像素点个数为3，但由于其到达图像边缘，因此选择横向进行修复，即φ(m)=L(φ(c),φ(i))。若2个方向的待修复像素点都到达边缘，因可利用信息太少，不对该区域进行修复。

4 实验结果

为验证所提出的算法，采用文献[12]474所提供数据进行试验验证。该数据为美国Long’sPeak(Colorado)地区附近山地高程数据对应的干涉测量相位图像，存在大量的悬崖等陡峭地形，相位图像的相干性比较差，如图3所示。算法中所使用的质量图通过文献中提供的相关系数图可以获得。在实验中，采用的平滑函数为

实验中，将本文提出算法与不采用质量图引导的算法、Goldstein枝切法[3]和最小二乘算法[12]248进行比较。从图3e)可以得出：本文算法能够收敛到满意解。图3d)为本文算法的解缠结果，相对于不采用质量图的方法，本文方法能对非连续区域取得较好的降噪结果。图3g)和图3h)分别为采用Goldstein枝切法和最小二乘算法的解缠结果。

图4为对另一块复杂地形相位图像的解缠结果比较，对于图4b)中矩形框中的非连续区域，本文算法能够较好地解缠，如图4c)所示；但不采用质量图的方法不能对该区域正确解缠，如图4d)所示。

本文定义均方误差来对解缠结果进行定量分析，解缠结果的均方误差定义为

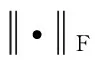
图3 真实地形解缠结果比较图(区域1)

图4 真实地形解缠结果比较图(区域2)

算法图3a)相位图像图4a)相位图像Goldstein枝切法0.04700.0112最小二乘算法0.09820.0266非质量图引导的算法0.08580.0158本文算法0.00700.0097

综上实验，本文的算法能够对复杂相位图像得到正确的解缠结果，并且对原始图像中的非连续区域具有一定的保留作用。

5 结 束 语

本文运用质量图与马尔科夫随机场建模相结合的方式对复杂相位解缠问题进行求解，将基于马尔科夫随机场建模方法应用于相位解缠问题中，所研究的建模和求解算法对于真实的复杂相位图像能够取得较好的解缠效果。特别是文中提出的通过最小方向线性插值方法对相位图像中质量较差的区域进行修复的算法，能有效修补由于质量图较差导致解缠后绝对相位的不连续性。但是，算法的效果和效率与质量图的选取有一定关系，下一步的研究应侧重于如何生成或者选择质量图以取得更加精确的解缠结果。

)

[1]SEAL D,ROGEZ F.SRTM As-flown mission timeline[R].Pasadena,California：JPL NASA,2000：1.

[2]FRIEDLANDER B,FRANCOS J M.Model based phase unwrapping of 2-d signals [J].IEEE Transactions on Signal Processsing，1996(44):2999-3007.

[3]曾凡光，吴光敏，MAI J D，等.Goldstein枝切法对存在间断相位缺陷的解缠研究[J].激光技术，2014，38(3)：335-341.

[4]HUANG Q,ZHOU H,DONG S,et al.Parallel branch-cut algorithm based on simulated annealing for large-scale phase unwrapping [J].IEEE Transactions on Geoscience and Remote Sensing,2015，53(7):3833-3846.

[5]JIAN G,Reliability-map-guided phase unwrapping method [J].IEEE Geoscience and Remote Sensing Letters,2016，13(5):716-720.

[6]王军飞，彭军还，杨红磊，等.改进金分发的InSAR相位解缠算法[J].测绘科学，2016，41(12):85-88.

[7]于宏，王成恩，于嘉鹏，等.基于粒子群算法的复杂产品装配序列规划[J].东北大学学报,2010,31(2):261-264.

[8]LU Y G,WANG X Z,ZHANG X P.Weighted least-squares phase unwrapping algorithm based on derivative variance correlation map[J].Optik,2007(118):62-66.

[9]GUO Y,CHEN X T,ZHANG T.Robust phase unwrapping algorithm based on least squares[J].Optics and Lasers in Engineering，2014，63:25-29.

[10]MACIEL L D S，ALBERTAZZI A G.Swarm-based algo-rithm for phase unwrapping[J].Applied Optics,2014,53(24):5502-5509.

[11]李泓宇,宋红军,王辉,等.质量图指导的改进的基于 CMRF 模型的自适应 InSAR 相位滤波[J].科学技术与工程,2015 (25):55-60.

[12]GHIGLIA D ,PRITT M.Two-dimensional phase unwrapping:theory,algorithms,and software[M].Hoboken,NJ:Wiley,1998:248-474.

(编辑：李江涛)

A Phase Unwrapping Method of Interferometric SAR Phase Image Based on Quality Map Guided Model

HAO Hongxing1， YU Ronghuan1， ZHANG Xitao2

(1. Science and Technology on Complex Electronic System Simulation Laboratory, Equipment Academy, Beijing 101416,China； 2. Department of Graduate Management, Equipment Academy, Beijing 101416, China)

Interferometric synthetic aperture radar (SAR) has been widely used in remote sensing field, such as digital elevation data acquisition, and phase unwrapping is one of the key steps in interferometric measurement. The paper transfers phase unwrapping to the minimization of an energy function based on the quality map guided Markov Random Field model, and solves the Markov Random Field problem with the algorithm of sequence tree weight message transfer. The paper also proposes to restore the pixels with phase image of poor quality by minimum direction linear interpolation, that is, based on the position of the pixels of poor quality, the interpolation repair is made to them in the shortest direction, to achieve complete unwrapping. Experiments show that the proposed algorithm can unwrap complex phase images generated by the varied real terrain, compared with the unwrapping algorithm like Goldstein branch cut method and methods without the quality map.

remote sensing information; interferometric synthetic aperture radar (InSAR); phase unwrapping; digital elevation model; Markov Random Field

2017-04-17

部委级资助项目

郝红星(1987—)，男，助理研究员，博士，主要研究方向为多媒体与虚拟现实、雷达信号处理。hongxinghao87@126.com

TN957； P237

2095-3828(2017)03-0008-06

A DOI 10.3783/j.issn.2095-3828.2017.03.002