基于鲁棒调节和目标值滤波的CMG群力矩控制

夏长峰， 蔡远文， 任 元， 王英广

(1. 装备学院 研究生院， 北京 101416； 2. 装备学院 航天装备系， 北京 101416； 3. 北京控制工程研究所， 北京 100190)

基于鲁棒调节和目标值滤波的CMG群力矩控制

夏长峰1， 蔡远文2， 任 元2， 王英广3

(1. 装备学院 研究生院， 北京 101416； 2. 装备学院 航天装备系， 北京 101416； 3. 北京控制工程研究所， 北京 100190)

为实现控制力矩陀螺群高精度快响应力矩控制，提出了一种基于鲁棒调节和目标值滤波的控制方法。建立了采用永磁直流无刷力矩电机的框架伺服系统数学模型,根据被控对象的传递函数设计了鲁棒调节器，针对装置状态可观测的特点对鲁棒调节器进行了简化，提出了镇定补偿器和伺服补偿器的关键参数计算方法，实现了转速控制的渐近调节且确保了动态性能指标，并提出采用目标值滤波器进一步加强系统的动态跟踪性能；在此基础上，依托金字塔安装构型的控制力矩陀螺群实现了系统力矩快速精确输出。MATLAB仿真结果表明：所提出的控制算法对1 N·m的力矩阶跃信号控制误差较传统比例-积分-微分算法降低了65.7%，响应时间减少了37.2%；对sin(20πt) N·m的正弦力矩跟踪时，可将力矩输出误差稳定在±2.1%之间。

控制力矩陀螺；目标值滤波；鲁棒调节；框架伺服系统；金字塔构型；高精度快响应控制

随着我国航天事业的飞速发展以及航天任务的多样化，对航天器姿态控制系统的快速机动响应能力提出了更高要求[1]。控制力矩陀螺(Control Moment Gyroscope，CMG)输出力矩大，响应速度快[2-3]，是飞船、卫星、空间站等航天器进行姿态快速机动需采用的关键执行机[4]。由CMG群构成的姿态控制系统是航天器进行姿态快速反应，以及精确控制的首选方案。CMG由高速转子系统和框架速率伺服系统组成，其中，高速转子提供大小恒定的角动量，框架强制转子改变角动量方向，从而使CMG输出力矩，对航天器进行姿态调整[5]。因此，CMG框架系统的控制精度、响应速度将直接影响CMG的力矩输出效果[6]。当CMG群作为航天器姿态控制系统的执行机构时，为了最大限度地克服各种干扰对控制效果的影响，必须深入研究其框架伺服系统力矩输出的高精度快速响应控制方法。

目前，多数伺服控制系统采用比例-积分-微分(Proportional-Integral-Differential，PID)控制算法，该方法原理简单且易于实现，但是由于对系统的不确定性参数敏感，机动性差，无法获得理想的随动跟踪效果[7-9]。文献[10]以高精度光电码盘作为角位置传感器，以数字信号处理器(Digital Signal Processor，DSP)作为数字控制硬件核心，设计了PID三环控制器，该方案下的框架伺服系统达到了较好的控制精度。但由于PID控制算法本身的局限性，无法使系统动态响应兼顾快速性和精确性。文献[11]分析了频繁机动条件下由CMG群进行侧摆机动的可行性，并根据CMG群构型设计了控制律，通过仿真验证了该方法可以使航天器姿态角快速、精确地达到机动要求，但文中没涉及框架伺服系统控制问题。为提高航天器姿态控制系统CMG群力矩输出精度，文献[12-15]采用观测器和补偿算法，但观测器精度和带宽有限，且观测存在一定滞后，会影响动态响应效果，无法实现动态力矩高精度输出。文献[16]和文献[17]分别采用模糊控制器和自抗扰控制器来抑制航天器干扰力矩，在低频条件下可以实现高精度力矩输出，但对高频指令力矩跟踪效果不佳。

本文在建立框架伺服系统数学模型的基础上，提出基于鲁棒调节和目标值滤波方法对CMG框架角速度进行快速精确控制，同时采用基于金字塔构型的CMG群实现高精度快响应力矩输出。仿真实验结果表明:该方法具有良好的机动性和较高的跟踪精度。

1 框架伺服系统建模

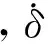
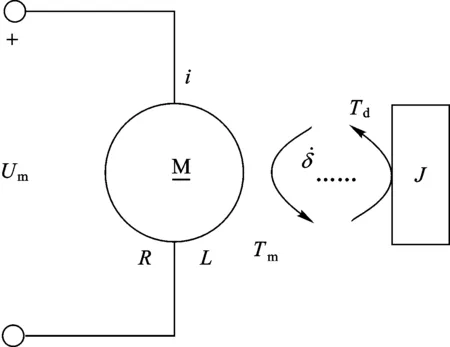
图1 框架伺服系统结构示意图

根据电机的电压平衡方程可以得到电机驱动电压Um与电枢电流i关系如下：

(1)

式中，Ke为反电动势系数。

假定框架力矩电机在电流环闭环的工作情况下为理想的力矩器，转矩系数为Km,则电机的电磁转矩Tm表达式为

Tm=Kmi

(2)

对电机轴分析，由牛顿定律可以得到

(3)

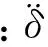
根据式(1)～(3)可确定该伺服系统结构框图，如图2所示。

图2 框架伺服系统结构框图

根据图2，可以确定被控对象传递函数为

(4)

令a=LJ/Km,b=(Lf+JR)/Km,c=(fR+KeKm)/Km,则式(4)可表示为

(5)

2 基于鲁棒调节和目标值滤波的力矩控制

2.1 基于鲁棒调节和目标值滤波的控制器设计

现有伺服系统大多采用常规PID控制器，这是一种一自由度控制器，该控制器结构简单，通过调节控制器的比例系数Kp、积分系数Ki、微分系数Kd，使系统获得良好的稳态精度，能够满足一般的控制系统要求；但难以同时保持快速性和准确性，因此对于高性能的控制系统有局限性，不易获得理想的控制效果[9]。鲁棒调节器是一种二自由度控制器，可满足兼顾精确性和跟随性的要求[18]。

本文将鲁棒调节器推广应用于框架伺服控制系统，并对其进行改进。鲁棒调节器由伺服补偿器和镇定补偿器两部分构成，分别用于实现渐近调节和确保动态指标。鲁棒调节控制系统如图3所示，其中，T(s)为伺服补偿器，K(s)为镇定补偿器，G(s)为被控对象。

图3 鲁棒调节器结构框图

如果把系统本身的状态输出反馈当作镇定补偿器，且所有状态可直接观测，则图3可以简化为图4的形式。图4中，伺服补偿器决定系统的跟踪特性，镇定补偿器决定系统的反馈特性，二者相互独立。因此，同时提高系统的跟踪特性和反馈特性成为可能，即系统的跟踪特性可由T(s)单独决定，反馈特性由K(s)单独决定，从而实现二自由度的控制。

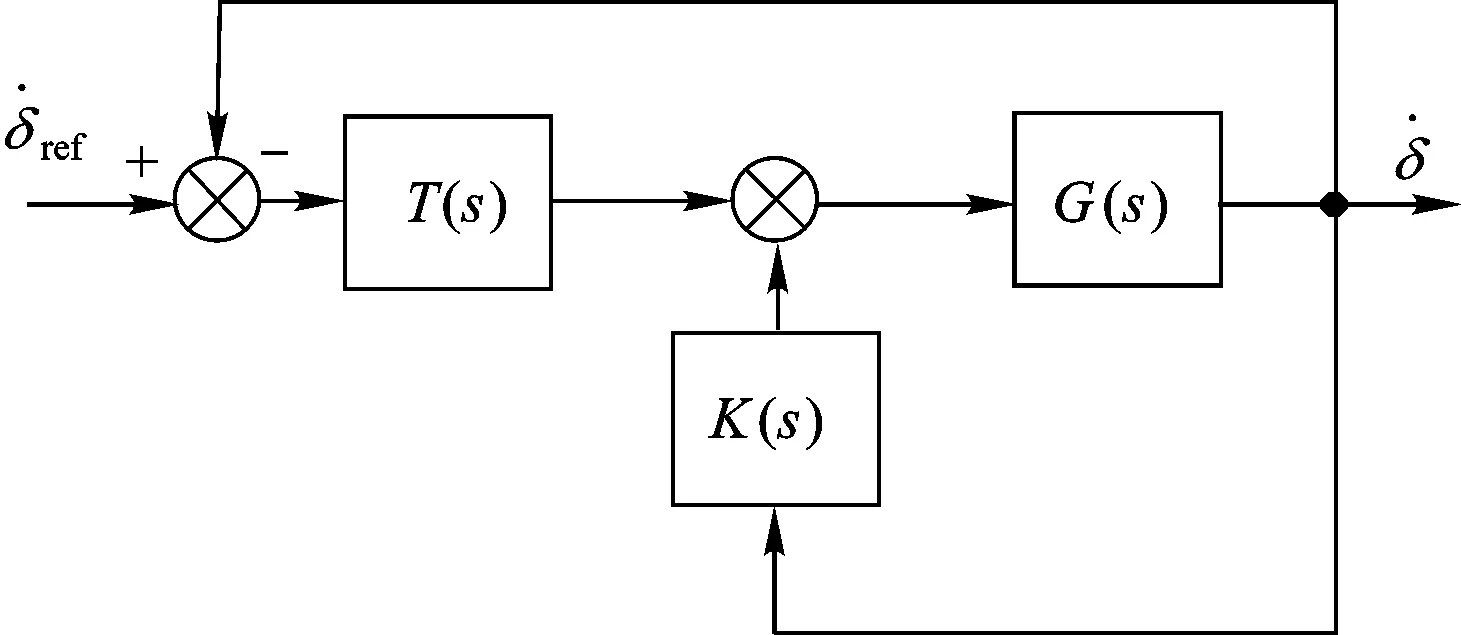
图4 简化的鲁棒调节器结构框图

令T(s)=(a0+a1s)/s,K(s)=k0+k1s,则框架伺服控制系统闭环传递函数可以表示为

(6)

对框架系统控制器进行设计，一方面要考虑使系统传递函数零点与系统的谐振极点相重合，从而形成偶极子的谐振抑制；另一方面要考虑控制器能够满足系统的恒速控制和随动控制的要求。因此，构造系统的闭环目标函数如下：

(7)

式中:ξ为阻尼率；ωn为自然角频率。根据式(6)、(7)，采用待定系数法计算控制器参数，可得

(8)

为了进一步加强系统的动态跟踪性能，通过在信号输入端添加目标值滤波器F(s),实现快速响应跟踪控制。其中，目标值滤波器表达式为[19-20]

(9)

式中:Ti、Td分别为控制器的积分时间和微分时间；α为可调参数。目标值滤波器通过改变α数值实现对跟踪速度的调节。则改进的框架伺服系统控制结构，如图5所示。

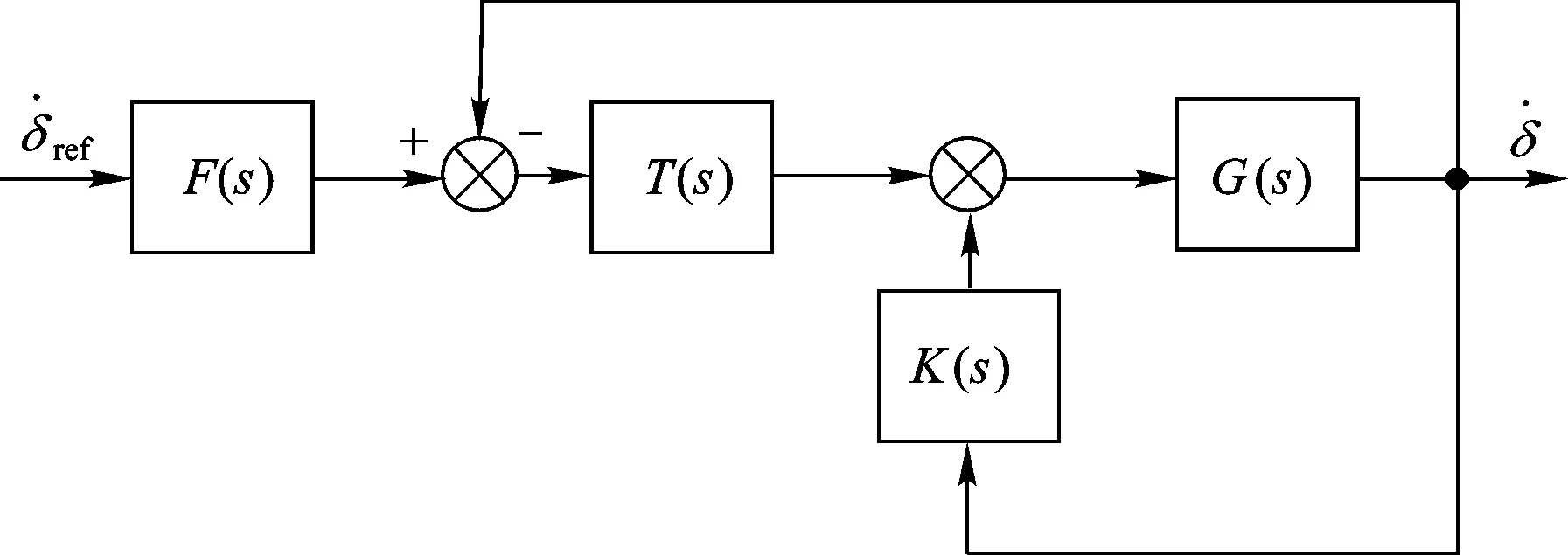
图5 改进的框架伺服系统控制结构框图

2.2CMG群力矩输出

本文采用由4个CMG构成的金字塔结构CMG群作为力矩输出执行机构[21-22]，在本体坐标系(Oxyz)中的几何关系如图6所示。图6中，β为CMG的安装倾角，δi为第i个CMG的框架角(i=1,2,3,4)，hi为第i个CMG的角动量。则CMG群的角动量和h为

(10)

式中，h1～h4的表达式分别为：

(11)

(12)

(13)

(14)

式中:角动量幅值h0=Jω,J为转动惯量,ω为CMG转子转速。

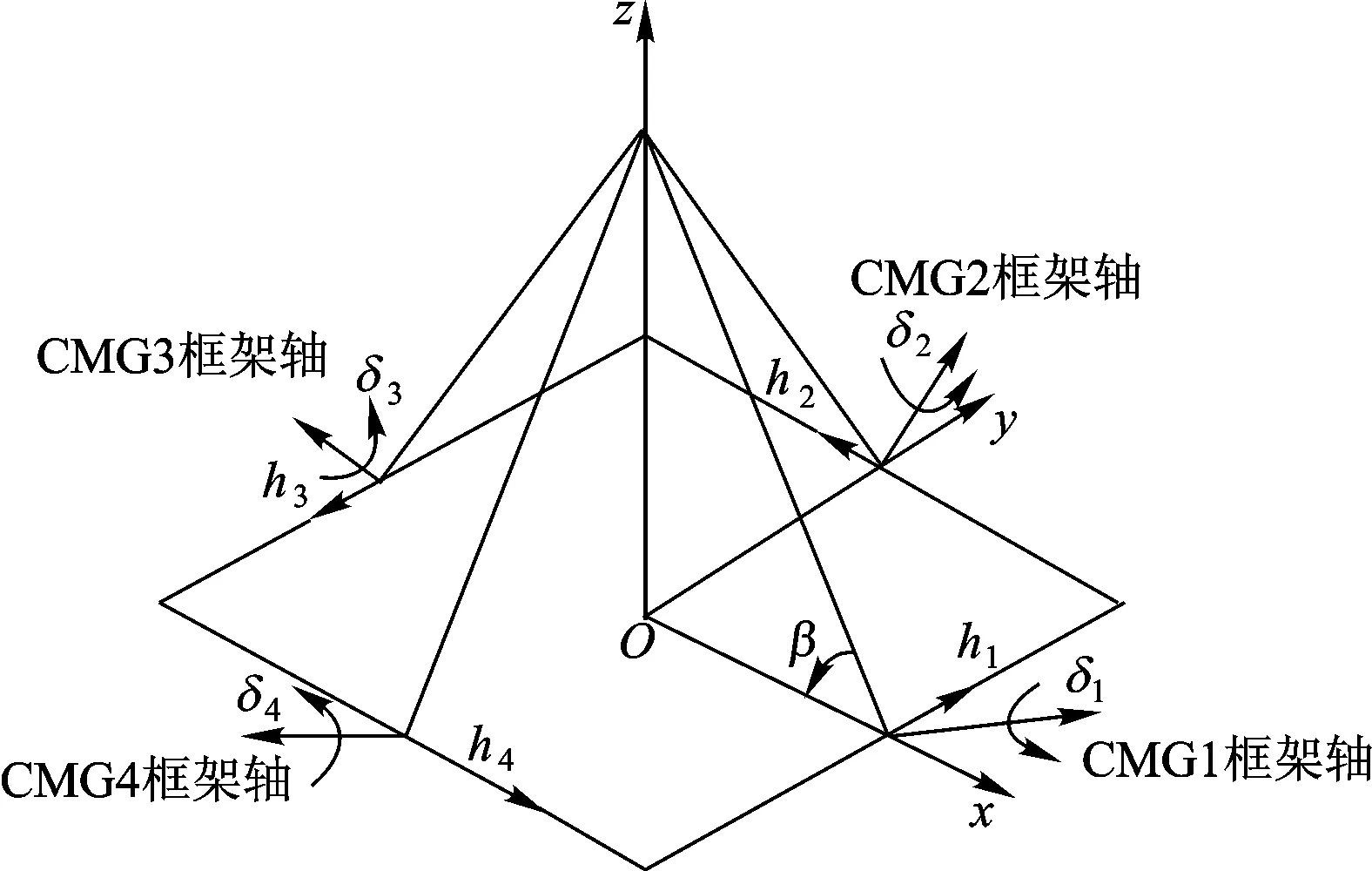
图6 金字塔构型CMG群

根据欧拉定理对式(10)求导，可得金字塔构型CMG群所能提供的输出力矩T为

(15)

3 仿真分析

为了验证所提出控制方法的有效性，在MATLAB软件的Simulink环境下建立CMG群快速响应仿真模型，并与传统的PID控制算法仿真结果进行对比，仿真系统主要参数如表1所示，其中，PID算法参数参照文献[23]进行设置。

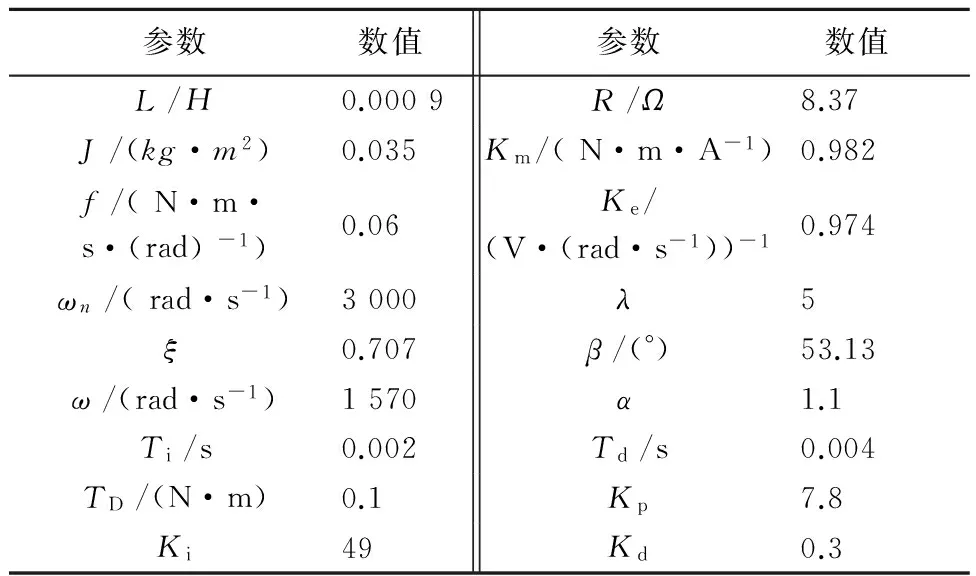
表1 仿真系统参数

3.1 框架角速度跟踪仿真

图7 阶跃角速度响应

将本文提出的鲁棒调节器结合目标值滤波算法，应用于框架伺服系统仿真平台中进行仿真分析，同时将传统的PID控制算法应用于同一框架伺服系统。用1°/s的单位阶跃信号作为框架角速度给定信号，2种算法的角速度响应曲线对比结果如图7所示。由图7可知，传统PID控制器的上升时间为0.043 s，超调量为7.24%，调整时间为0.116s；本文所提出的控制算法上升时间为0.009 s，超调量为1.98%，调整时间为0.012 s。通过与传统PID控制器对比可看出，所提出的鲁棒调节结合目标值滤波得到的角速度响应时间短，超调量小，虽然与指令信号完全重合所需时间略长于PID算法，但是其进入终值±3%范围的稳定状态更快，具有更好的跟随性。其原因在于与PID控制器相比，目标值滤波器结合伺服补偿器可以实现对指令信号的快速跟踪，镇定补偿器可以对误差进行准确补偿。

当框架角速度指令信号为频率10 Hz、幅值1°/s的正弦信号时，2种方法得到的角速度响应曲线如图8所示。根据图8可以看出:输入信号频率为10 Hz情况下，传统PID控制方法对输入信号的跟踪存在幅值衰减和相位滞后；鲁棒调节结合目标值滤波控制方法可以对输入信号的幅值和相位保持一致跟踪。其原因在于鲁棒控制器中的伺服补偿器和目标值滤波器可以对输入信号进行快速跟踪，镇定补偿器可以对跟踪误差进行准确补偿。此时，采用鲁棒调节结合目标值滤波控制算法的角速度误差信号如图9所示。由图9可知，角速度误差范围在±0.032°/s之间。综合图8和图9可知，只有基于鲁棒调节结合目标值滤波的控制器符合系统的动态性能指标要求。

图8 正弦角速度响应

图9 角速度跟踪误差

3.2 CMG群力矩输出仿真

根据公式(15)可知，对指令力矩的有效跟踪是以对框架角速度的有效跟踪为前提条件。因此，在3.1节实现对框架角速度跟踪的基础上，对CMG群进行力矩输出仿真。计算机产生在星体坐标系下x轴方向上1 N·m的力矩阶跃信号指令，CMG群产生的x轴方向控制力矩响应如图10所示。从图中可以看出:基于经典PID的CMG群上升时间为0.042 s，超调量为8.16%，调整时间为0.153 s；基于鲁棒调节和目标值滤波算法的力矩输出系统上升时间为0.012 s，超调量为2.8%，调整时间为0.096 s。通过对比可知，与采用传统PID控制器的力矩输出系统相比，基于鲁棒调节结合目标值滤波的CMG群力矩波动量降低了65.7%，响应时间减少了37.2%。

图10 阶跃信号力矩输出响应

当指令力矩为x轴方向，幅值为1 N·m、频率为10 Hz的正弦信号时，CMG系统产生的x轴方向力矩响应如图11所示。从图11可以看出:基于传统PID算法的力矩输出系统无法保持对指令力矩的幅值和相位跟踪，动态性能较差；基于鲁棒调节结合目标值滤波的力矩控制方法能对指令力矩保持一致跟踪。本文提出的力矩控制方法产生的误差如图12所示。由图12可知，力矩控制系统初始误差为6%，最终误差保持在±2.1%之间,控制精度可以满足系统的精度指标要求。

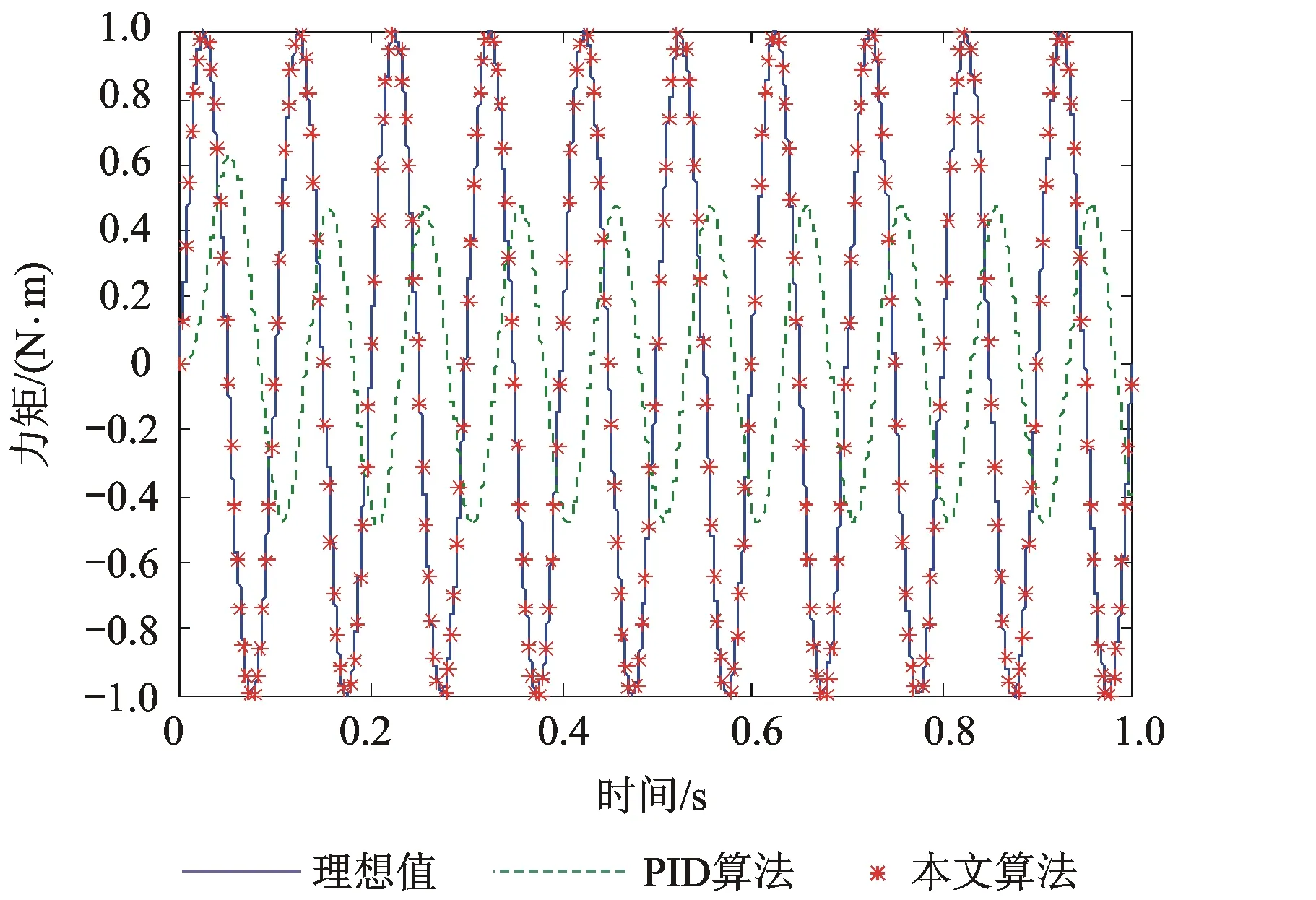
图11 正弦信号力矩输出响应

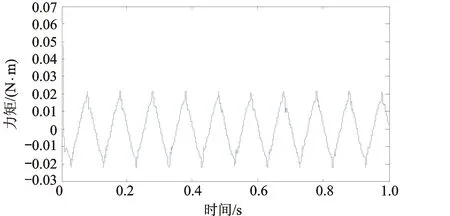
图12 正弦力矩跟踪误差

4 结 论

1) 鲁棒调节器中的镇定补偿器实现了对角速度误差的有效补偿，伺服补偿器结合目标值滤波器实现了对指令角速度的快速跟踪。仿真结果表明：阶跃角速度跟踪超调为1.98%，正弦角速度跟踪误差为±3.2%；

2) 本文提出的基于鲁棒调节和目标值滤波的金字塔构型CMG力矩输出系统，可实现对指令力矩的一致跟踪。仿真结果表明：与PID算法相比，所提出算法响应时间减少37.2%，阶跃力矩信号跟踪超调量减小65.7%，且可将正弦力矩跟踪误差保持在±2.1%范围内。

References)

[1]ZHENG S,HAN B.Investigations of an integrated angular velocity measurement and attitude control system for spacecraft using magnetically suspended double-gimbal CMGs[J].Advances in Space Research,2013,51(12):2216-2228.

[2]ABBAS H S,ALI A,HASHEMI S M,et al.LPV state-feedback control of a control moment gyroscope[J].Control Engineering Practice,2014,24: 129-137.

[3]REN Y,FANG J.High-precision and strong-robustness control for an MSCMG based on modal separation and rotation motion decoupling strategy[J].IEEE Transactions on Industrial Electronics,2014,61(3):1539-1551.

[4]CUI P,LI S,ZHAO G,et al.Suppression of harmonic current in active-passive magnetically suspended CMG using improved repetitive controller[J].IEEE/ASME Transactions on Mechatronics,2016，21(4):1-10.

[5]CHEN X C,CHEN M Y.A filtering control method of the gimbal rate-servo system in DGMSCMG based on strong tracking filter[J].Advanced Materials Research,2014,875-877:2164-2169.

[6]HAN B,ZHENG S,WANG Z,et al.Design,modeling,fabrication,test of a large scale single-gimbal magnetically suspended control moment gyro[J].IEEE Transactions on Industrial Electronics,2015，62(12):1-1.

[7]ZHAO L,ZHAI B,WU D,et al.A low speed servo system of CMG gimbal based on adaptive sliding mode control and iterative learning compensation[C]// IEEE International Conference on Mechatronics and Automation.[S.l.]:IEEE,2015:2249-2254.

[8]FU P,CHEN Z,CONG B,et al.A position servo system of permanent magnet synchronous motor based on back-stepping adaptive sliding mode control[J].Diangong Jishu Xuebao/transactions of China Electrotechnical Society,2013,28(9):288-293;301.

[9]CAI S,WU S,BAO G.Cylinder position servo control based on fuzzy PID[J].Journal of Applied Mathematics,2013(3):1-10.

[10]张峰,房建成.一种基于DSP的磁悬浮控制力矩陀螺框架伺服系统[J].微电机,2007,40(11):32-34.

[11]汤亮,徐世杰.采用单框架控制力矩陀螺群的卫星侧摆机动控制研究[J].航天控制,2003,21(2):1-5.

[12]SUN J J,PENG C.Disturbance observer control method in DGMSCMG[J].Electronics Letters,2014,50(14):989-990.

[13]PENG C,SUN J J.Disturbance observer control method in SGMSCMG[J].Proceedings of the institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2015,229(11):1998-2006.

[14]鲁明,张欣,李耀华.SGCMG框架伺服系统扰动力矩分析与控制[J].中国空间科学技术,2013,33(1):15-20.

[15]DESHPANDE V S,MOHAN B,SHENDGE P D,et al.Disturbance observer based sliding mode control of active suspension systems[J].Journal of Sound & Vibration,2014,333(11):2281-2296.

[16]CHOU M C,LIAW C M.Dynamic control and diagnostic friction estimation for an SPMSM-driven satellite reaction wheel[J].Industrial Electronics IEEE Transactions on,2011,58(10):4693-4707.

[17]PENG C,FANG J C.High-precision control for double-gimbal magnetically suspended control moment gyro via composite anti-disturbance control[J].Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering,2014,229(7):1183-1193.

[18]涂奉生.鲁棒(Robust)调节器[J].信息与控制,1979(4):85-91.

[19]熊志强,王炜,邱祖廉.一种二自由度PID的实现[J].控制理论与应用,2003,22(4):17-19.

[20]SHI J J,ZHANG L X,JIANG A Q.Application on two degree of freedom model driven PID in liner first-order inverted pendulum[J].Applied Mechanics & Materials,2013,433-435:1000-1004.

[21]ZHANG J,JIN J,LIU Z.An improved installation for control moment gyros and its applications on reconfiguration and singular escape[J].Acta Astronautica,2013,85(11):93-99.

[22]王平,王华,任元.基于MSCMG金字塔构型的航天器姿态测控一体化控制方法[J].系统工程与电子技术,2016,38(1):123-129.

[23]何芝强.PID控制器参数整定方法及其应用研究[D].杭州：浙江大学,2005：12-24.

(编辑：李江涛)

Torque Control of CMG Cluster Based on Robust Controller
and Target Value Filter

XIA Changfeng1， CAI Yuanwen2， REN Yuan2， WANG Yingguang3

(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China; 2. Department of Space Equipment , Equipment Academy, Beijing 101416, China; 3. Beijing Institute of Control Engineering, Beijing 100190, China)

In order to realize high-precision and fast-response torque control of Control Moment Gyroscope (CMG) cluster, a control algorithm based on target value filter and robust controller is put forward. The mathematical model of gimbal servo system which adopts permanent magnet brushless direct current torque motor in CMG is set up. The robust controller is designed according to the transfer function of the controlled object, and then it is simplified based on the observable characteristics of the device status. The calculation method of key parameters in stabilizing compensator and servo compensator is proposed. In this way, asymptotic adjustment of rotational speed is achieved and the dynamic performance index is guaranteed. Besides, dynamic tracking performance of the system is further strengthened with the proposed target value filter, on the basis of which，fast and precise system torque output is realized with the pyramidal CMG cluster configuration. MATLAB simulation results show that the control error of 1 N·m step torque is reduced by 65.7% and response time is decreased by 37.2% with the proposed algorithm compared to traditional Proportional-Integral-Differential (PID) method. The error of sin(20πt)N·m sinusoidal torque is stabilized between -2.1% and +2.1% with the proposed method.

control moment gyroscope (CMG); target value filter; robust controller; gimbal servo system; pyramidal central configuration; high-precision and fast-response control

2017-03-14

国家自然科学基金资助项目(51475472，61403396)

夏长峰(1989—)，男，博士研究生，主要研究方向为先进惯性测量与控制技术。superxiacf@163.com 蔡远文，男，教授，博士生导师。

TP2

2095-3828(2017)03-0086-06

A DOI 10.3783/j.issn.2095-3828.2017.03.015