卫星波束标校信号码型对比分析

刘会红，陈敬乔

（中国电子科技集团公司第五十四研究所 石家庄 050081）

引言

由于卫星上天之后经历的空间环境比较复杂，光照的改变和剧烈的温度变化等都容易引起天线各通道的相位幅度变化，加上天线器件的不一致性以及制造公差和装配误差等因素的影响，导致GEO 星载天线系统通道间幅度和相位不一致[1]。如果不进行有效的检测与校正，直接进行星上射频波束合成会导致波束指向出现偏差，甚至会指向错误[2−4]。因此，在卫星入轨后，需要对其天线系统进行周期性的标校。

波束标校是指采用能量测向体制来进行波束指向测量，根据测量结果调整波束指向中心，从而保证天线波束覆盖满足系统要求。移动通信卫星在寿命期内难以保持位置固定，卫星星下点位置会以天为单位，周期性进行漂移，这会导致波束指向的不确定，不能满足应用系统对波束指向精度的要求，影响了系统的正常使用。

波束指向的不确定性主要会对应用系统产生两方面影响[5−7]：首先，会引起用户收发电平的波动，会对系统工作带来不良影响；其次，指向中心的漂移会造成用户终端所处地理位置与真实波束中心之间距离的偏差，使用户初始接入时隙不确定范围加大，影响随机接入信道的使用效能。

星载天线的在轨标校大致可分为阵内标校和阵外标校[8−10]。阵内标校即在卫星上安装校正设备，星上自主完成标校；阵外标校是指通过地面终端站、标校站辅助完成相控阵天线的标校。国外很早就开始了对星载阵天线波束标校的研究。国内中电十所、三十八所等多家科研机构对相控阵天线及波束标校方面也有较深入的研究[11−17]。

由于阵内标校算法会增加星上设备重量及复杂性，对卫星可靠性提出了更高要求。部分通信卫星由于体积重量的限制，无法采用阵内标校，因此天线标校主要采用适应性更强的阵外标校法进行。

为了保证应用系统的使用性能，降低地面应用系统设计复杂度，提高资源利用率，需要在采用三轴姿态动态偏置的基础上，再采用波束标校方式，进一步提高波束的指向精度，以满足应用系统使用要求。波束标校示意图如图1所示。

图1 波束标校示意图Fig.1 Wave-beam calibration sketch map

在波束标校系统中，标校信号码型的选择十分关键，常用的标校信号有m 序列信号、Walsh 信号、单频信号和Chirp 信号（扫频信号）等。其中m 序列信号、Walsh 信号均属于PN（Pseudo-Noise）序列，有较好的相关性；Chirp 信号为扫频信号。这几种信号各有特点，在实际中可以从实现复杂度、抗干扰性能、估计能量精度，捕获特性等四方面综合考虑加以选择。

1 波束标校原理

在下行标校方式中，GEO卫星波束标校系统接收天线位于如图2 所示点O。当S、N、W、E 四个标校波束的等功率点O'与点O重合，在点O处接收到四个波束的功率电平相等；当四个波束的等功率点O'与点O不重合，则在点O处接收到四个波束的功率电平有差异，根据4 个功率电平的差值大小，可计算出标校波束等功率点O'与点O的位置差。

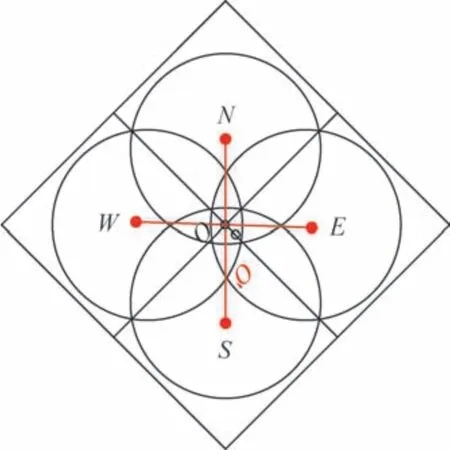
图2 标校原理Fig.2 Calibration principle

为了充分利用接收数据，可以采用相关的方法测时差。为了降低卫星功率波动造成的测量误差，本系统采用归一化差分指向误差测量方法，设东向波束测量功率值为E2，西向波束测量功率值为W2，南向波束测量功率值为S2，北向波束功率测量值为N2，则俯仰指向误差为：

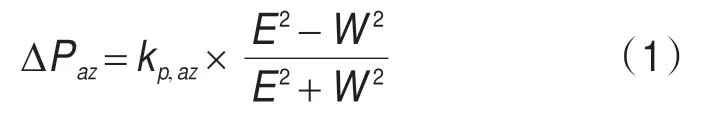
滚动误差为：

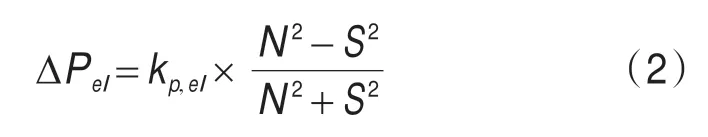
其中，kp,az和kp,el分别为俯仰和滚动测量校正因子。

2 不同类型标校信号性能对比

2.1 抗干扰性能对比

m 序列信号、Walsh 信号和Chirp 信号均具有一定的抗干扰能力，m序列信号抗干扰能力与扩频比相关，Walsh 信号抗干扰能力与Walsh 码长度相关，Chirp 信号抗干扰能力与扫描带宽相关。由于波束标校信号中不调制信息，因此可以通过对伪随机序列或Walsh 序列的积累来进一步提高抗干扰能力。以伪随机信号积分长度为2 047 个码片为例，伪随机序列可获得最大33 dB 的抗干扰能力；而长度为2 048的Walsh码序列也可获得最大33 dB的抗干扰能力，Chirp 信号抗干扰能力与压缩比相关，如果Chirp信号选择Thuraya系统中FCCH信道采用的信号，处理增益为18.74 dB，抗干扰能力不如m序列信号和Walsh信号。因此从抗干扰角度看，伪随机序列信号和Walsh信号最好，Chirp信号次之，单频信号最差。各码型抗干扰能力对比见表1。

表1 各码型抗干扰能力对比Table 1 Comparison of anti-interference ability of each code type

2.2 实现复杂度对比

Chirp 信号不易采用模拟方式实现，而数字实现需采用向量方式，特别是四个信号同时产生时，信号质量与占用带宽、数模转换（Digital to Analog，DA）精度等参数有关，另外对Chirp信号的接收处理也有较大难度。

m 序列方式和Walsh 信号可以采用模拟也可以采用数字方式实现，由于伪随机序列和Walsh 信号本质都是0、1 码，因此可以通过波形存储或其他方式，降低m 序列信号形成难度。另外，伪随机序列或Walsh 序列的接收，由于没有调制信息，因此较一般扩频信号接收简单。单载波信号可以采用模拟方式生成，实现最简单。因此在实现复杂度方面，Chirp 最难，伪随机序列和Walsh 序列次之，单频方式最简单。各码型实现复杂度对比见表2。

表2 各码型实现复杂度对比Table 2 Comparison of implementation complexity of each code type

2.3 接收能量估计精度对比

由于Chirp 信号抗干扰能力弱于伪随机序列信号和Walsh 信号，实现又比伪随机序列信号和Walsh 信号复杂，因此，在性能方面只进行伪随机序列、Walsh 信号和单频信号高斯白噪声条件下的能量估计精度对比。

高斯信道下，接收机接收到的中频信号可表示为：

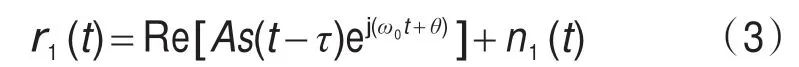
式中，n1(t)为高斯白噪声，单边功率谱密度为N0；s(t-τ)为基带信号波形，A为信号幅度；ω0、θ分别为载波角频率和载波相位；τ为信号传输时延。等效复基带信号表示为：

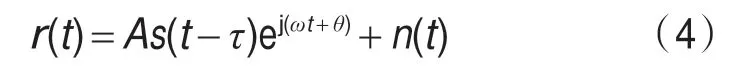
其中，n(t)为复高斯噪声，单边功率谱密度为4N0，且有：

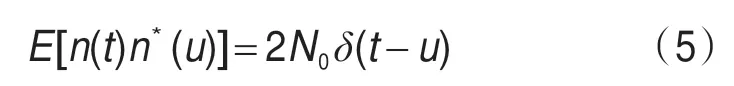
ω、θ分别为载波剩余频差和相差；s(t-τ)为接收到的基带信号波形，对于PSK调制信号，有：

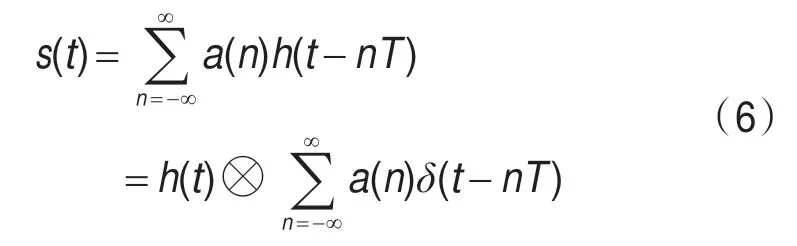
式中：⊗表示卷积；T为符号周期；a(n)为发送的符号序列。本文假定为i.i.d 序列（独立同分布），且有：

h(t)为信道脉冲响应。本文假定h(t)具有归一化能量，即：

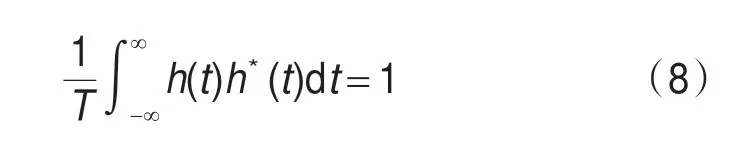
根据式(6)～式(8)，可得：

在观测时间间隔T'=LT内接收到的信号能量为：

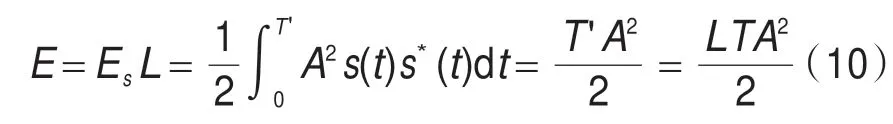
式中,L为观测符号数，Es为接收信号的每符号能量，T为符号周期。

估计信号幅度时，考虑式（4）的基带模型，并假定信号传输时延为0。在观测时间间隔T'内，接收信号r(t)的对数似然函数可表示为：

其中,F为常数，将上式对参量A求导，得到：

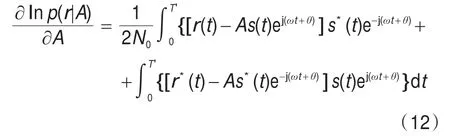
考虑到幅度A为实数，因此最大似然估计是下述方程的解：

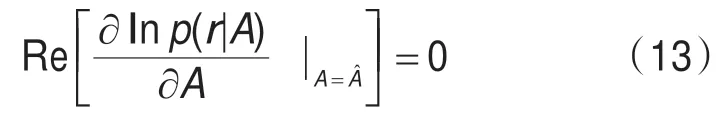
对上式求解，并考虑式（7）的条件，得最佳估计值：

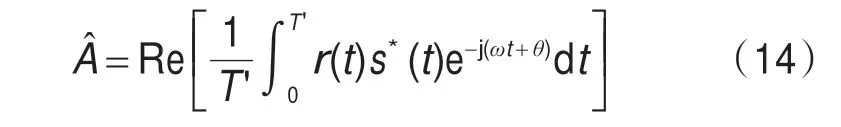
将式(4)代入式(12)，可得单参量估计时的费什尔信息矩阵F的元素：

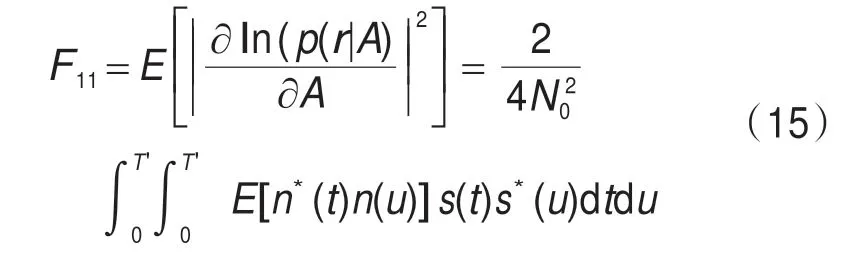
将式(5)代入上式，得到：

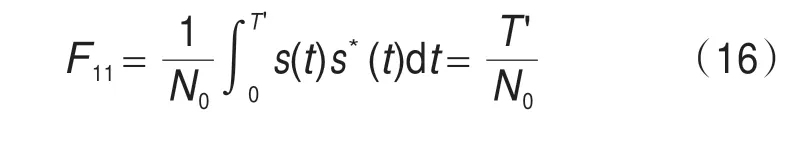
上式的推导利用了式(7)的条件。因此幅度估计的克拉美-罗界(Cramer-Rao Bound，CRB)为：

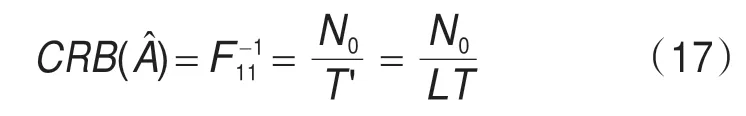
其中,T'为观测时间，L为观测的符号数，T为符号周期，N0为噪声单边功率谱密度。可见，估计方差随观测时间的增加而线性减小。根据式(17)，得到归一化幅度估计的CRB：

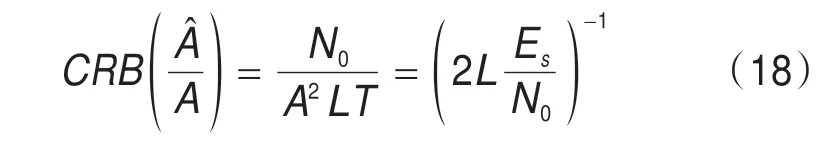
根据(14)式得出估计均值为：

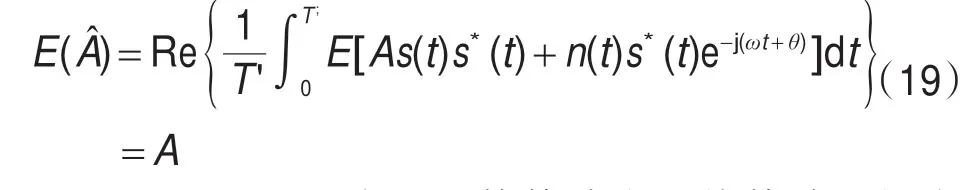
可见基于(14)式的最佳估计为无偏估计。幅度估计方差为：

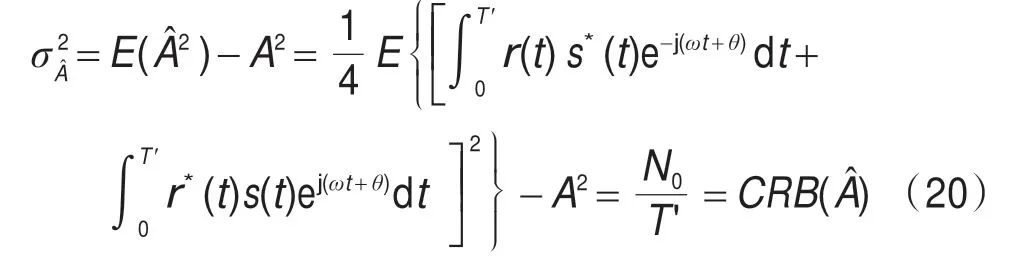
可见式（14）的最佳估计值的估计方差与CRB 一致，即PSK 信号的幅度估计方差仅与观测的符号数、符号周期及噪声单边功率谱密度有关，所以在相同的观测时间内，伪随机序列、Walsh 信号和单频信号在同一高斯白噪声条件下的幅度估计方差是相同的，即三者的能量估计精度相当。

幅度估计方差与观测的符号数L和均成反比，当分别为3 dB 时，归一化幅度估计方差与L的关系如图3所示。

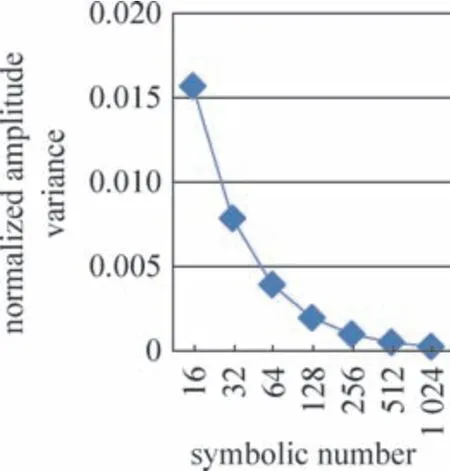
图3 归一化幅度估计方差与L的关系Fig.3 The relationship between normalized and L

2.4 捕获性能对比

标校信号捕获依赖于标校信号之间的正交性及其自相关特性。另外，在天线存在指向误差时，标校站接收信号功率不同，且最大的功率差异可达近30 dB，这给标校信号码型设计和标校信号的捕获带来了难度。

若采用长GOLD码低码率的设计方法，则为了保持各波束标校信号的正交性，接收端需进行整个码周期的相关匹配。以码片速率10 000 chip/s，积分长度为8 192个码片为例，匹配后的等效符号率仅为Hz 数量级，很难实现信号跟踪和能量测量。若采用部分匹配方式，码型正交性的破坏将使输出结果呈现出多值现象。图3 是生成多项式为x11+x2+1 的m 序列在各路信号接收功率不同且无噪声叠加情况下的捕获情况。其中x轴表示归一化载波频偏（Δf/Rc，Rc为码片速率），y轴表示归一化捕获峰值。由图4 可知，当信号间功率差达到24 dB 以上时，归一化峰值呈现出多值现象，将影响判决结果和测量精度。

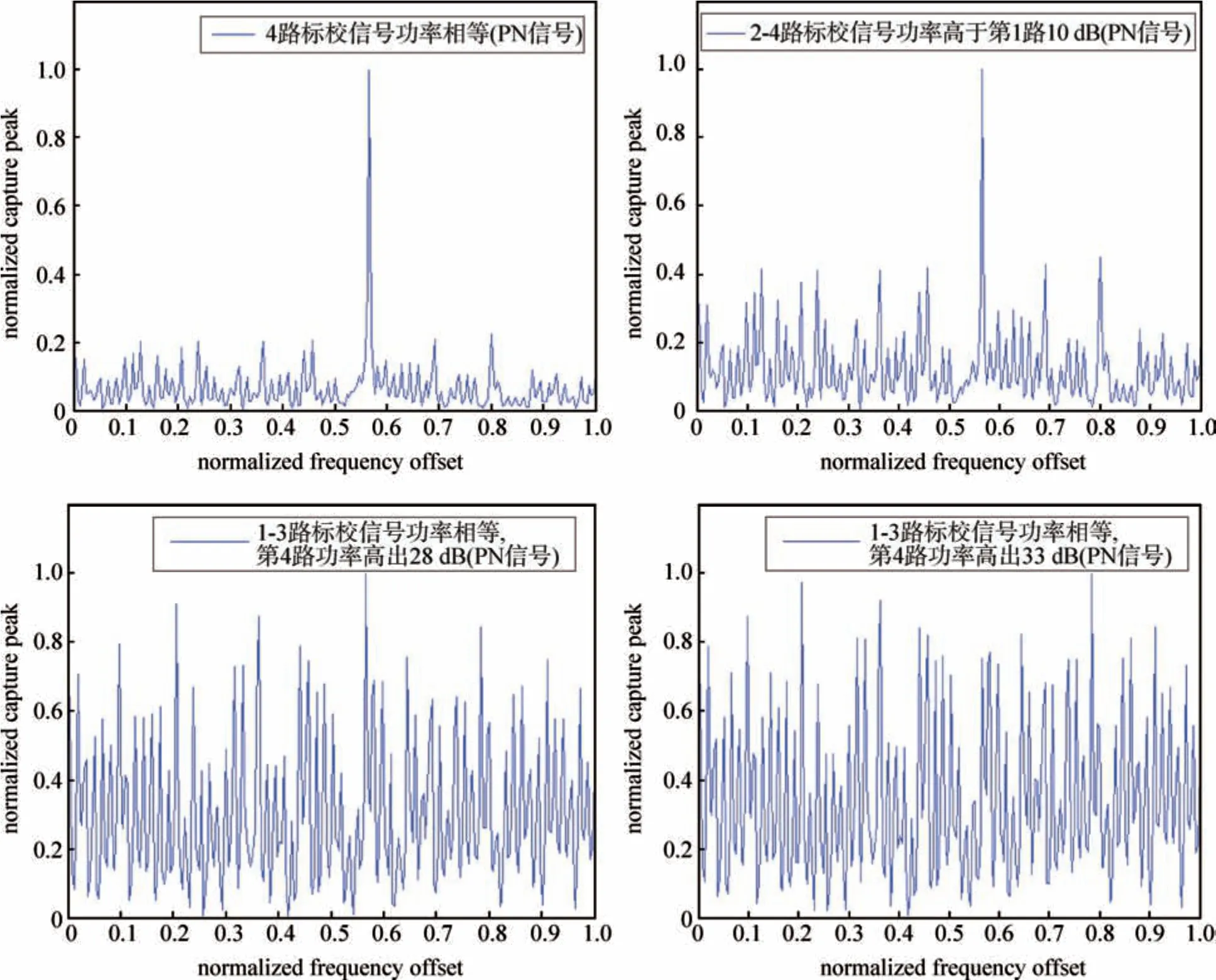
图4 不同情况下1号标校站m信号的捕获峰值Fig.4 Capture peak on No.1 calibration station under different conditions

由于系统能够保证下行标校信号之间的同步关系，所以标校信号可选择使用长度为256 的Walsh 码作为信息码，不同波束选择不同Walsh 码来区分；根据Walsh 码间的正交特性，在256 个码片的积分周期内，其他波束信号对本波束信号没有影响。图5 是采用256 位长Walsh 码，在各路信号接收功率不同情况下捕获接收时的归一化信号功率，由图可知，在各路信号等功率至信号功率最大相差30 dB 情况下，各路信号均呈现出较好的捕获特性。

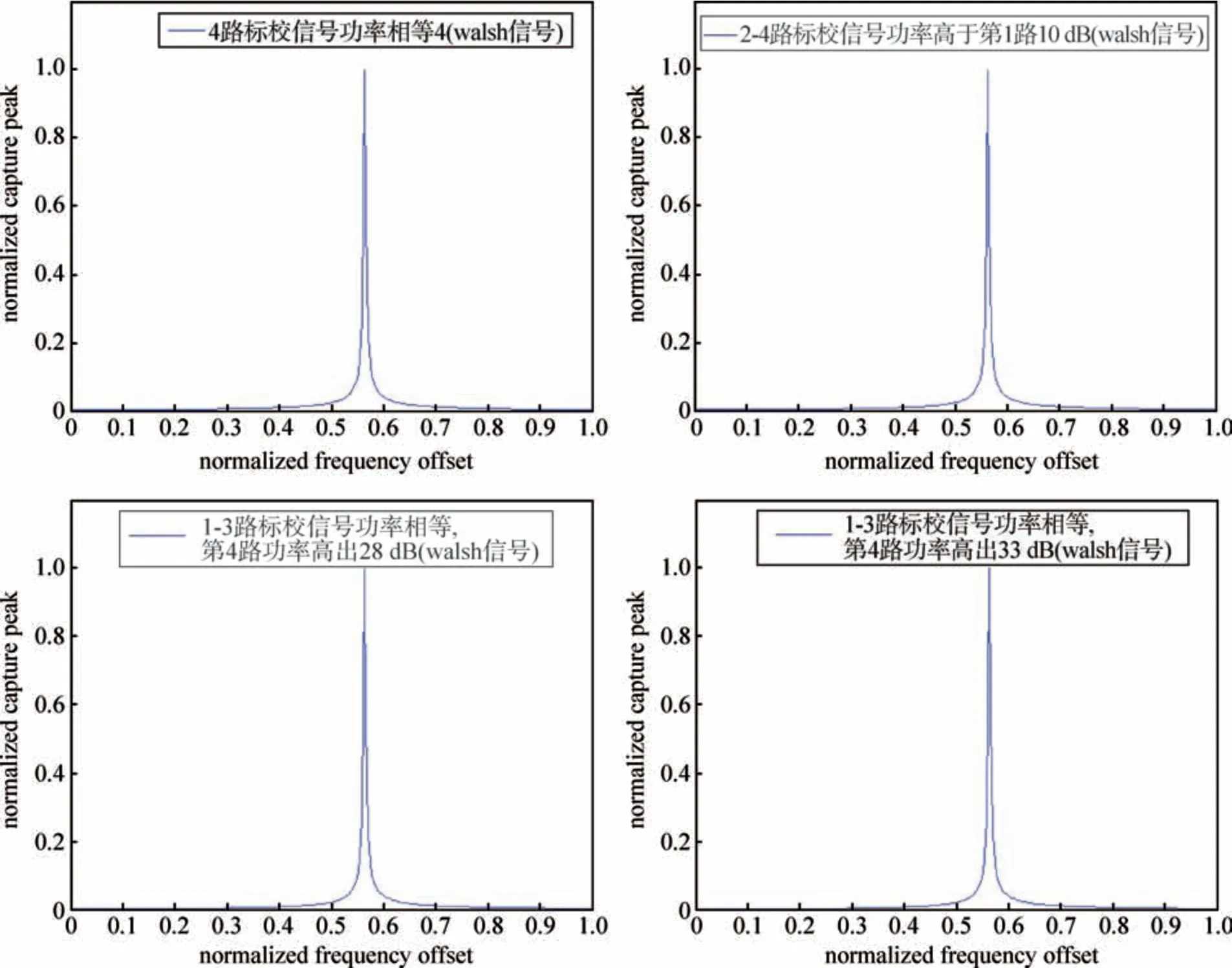
图5 不同情况下1号标校站Walsh信号的捕获峰值Fig.5 Capture peak of Walsh on No.1 calibration station under different conditions

就捕获性能来看，当两个标校站的接收信号功率之间存在很大的差异时，Walsh 信号的捕获性能要明显优于m 序列。所以，选择Walsh序列作为标校信号。

3 结束语

通过上文的分析可知：从抗干扰角度看，Walsh 信号和伪随机序列信号最好，Chirp 信号次之，单频信号最差；在实现复杂度方面，Chirp 最难，伪随机序列和Walsh 序列次之，单频方式最简单；就捕获性能来看，在两个标校站的接收信号功率之间存在很大的差异时，Walsh 信号的捕获性能明显要优于m序列。

因此，在系统能够保证下行标校信号之间的同步关系的前提下，综合考虑，标校系统选择Walsh序列作为标校信号较为合适。