基于多种预测模型的小批量物料生产安排*

王 静，丁学利

（阜阳职业技术学院）

0 引言

随着全球经济的快速发展，市场经济的需要也在不断变化，小批量、多品种的生产模式正在逐步演化成最主要的生产模式之一［1－2］.其生产特点主要集中体现在产品种类较多、结构复杂，而相比产量较少.就目前多品种小批量产品生产企业发展现状来看，在生产管理中依然还存在一些问题，例如，基础设施不完善、制度不健全、信息化生产水平低、生产进度滞后等，严重影响企业的高质量发展.现实中大多数企业，更加注重加强生产管理，提高产品生产效率及质量管控上，往往会忽略产品的生产安排.生产安排也是影响企业利润率的重要因素，如果能对生产计划进行精准预测，就能为企业节约不必要的人力、物力，从而创造更多收益.

近年来，对产品的生产控制和预测研究方面，大多建立在快速发展的机器学习方法基础上，BP 神经网络、支持向量机、极限学习机、以及各种群体智能算法是其中的代表.更多的研究集中于对智能算法的组合优化，如董海，徐德珉.基于加权LS－SVM 的批量产品标准差预测与质量控制［3］，高岩［4］提出组合模型的多品种小批量生产方式质量预测方法研究等.该文主要采用主成分分析［5－6］，根据综合得分先选出6 个重点关注物料.然后，建立BP 神经网络模型［7－8］对需求量进行预测，进而给出物料的生产计划安排，为企业的生产发展更上一层楼.

1 数据来源与分析

1.1 数据来源

该文以2022年“高教社杯”全国大学生数学建模竞赛［9］E题附件的数据为研究对象，见表1.

表1 原始信息

将附件数据第1次出现的时间（2019年1月2日）所在的周设定为第1 周，以后的从当周一开始至周日结束，例如，2019 年1 月7 ～13 日为第2 周，以此类推.

1.2 数据预处理

利用Excel 透视表对附件进行分析，整理出284个物料177周的信息，如周需求量和销售单价.以物料6004010174为例，见表2.

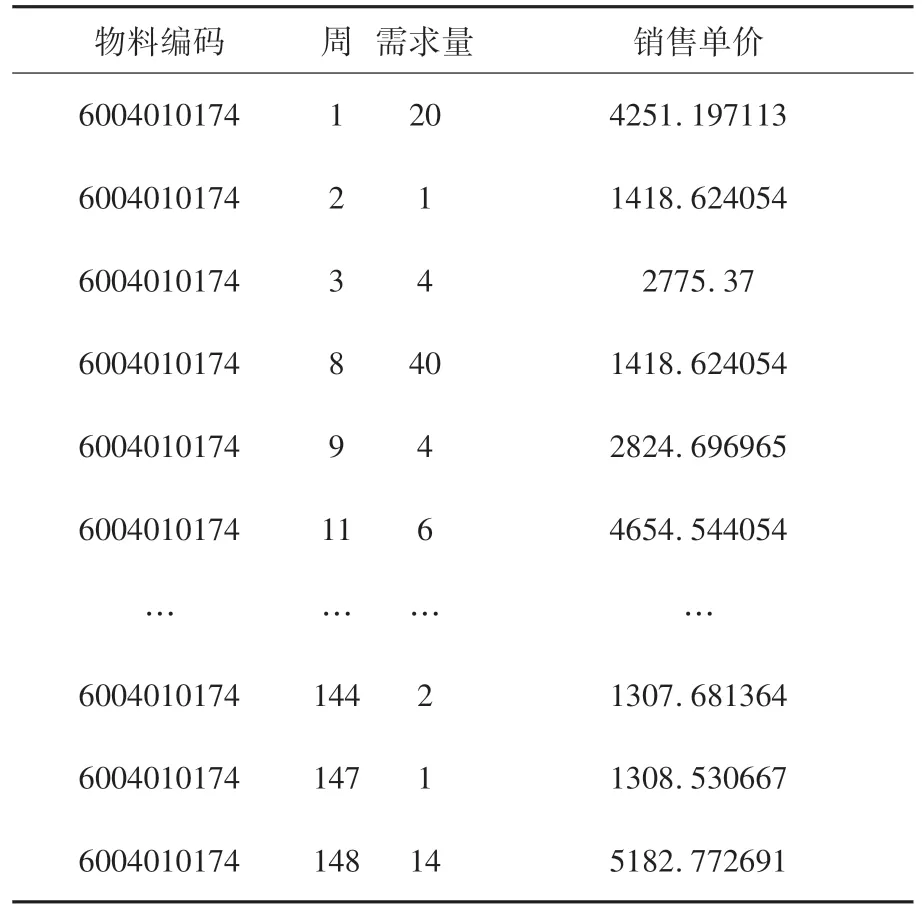
表2 物料6004010174的周信息

从表2 中明显发现第4 周，第5 周等无信息，默认无需求量.因此就把当周的需求量记为0，销售单价记为平均值.表3 为处理后的物料6004010174的信息.

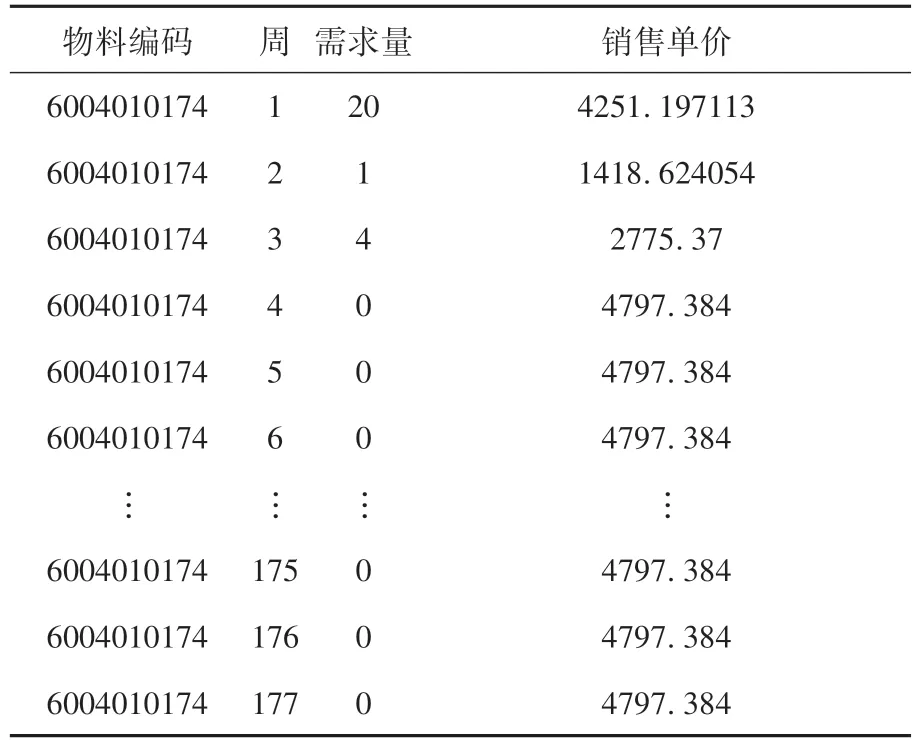
表3 处理后的物料6004010174的周信息

同理，填补出所有物料的177 周的数据，利用处理后的数据进行分析，建立预测模型.

2 重点关注物料

2.1 主成分分析

主成分分析［1］是设法将原来众多具有一定相关性（比如m 个变量），重新组合成一组新的互相无关的综合指标来代替原来的指标.

设有n个物料，每个物料有m 个变量，写成如下矩阵：

①先将矩阵标准化，然后建立变量的相关矩阵：

其中，R ＝（rij）m×m，rij为对应各数据之间的相关系数.

②求R的m个特征值及相应的特征向量ti（i ＝1，…，m）

③求主成分：

④精度分析

主成分yj贡献率：

⑤综合得分

2.2 重点关注物料选取

为找到6种重点关注的物料数据，先对附件中数据用Excel透视表进行整理，得到284 个物料共177周，进而整理出每个物料的总频数、总需求量、平均销售单价和周数（周数：物料出现周的数量），见表4.

物料编码 频数 总需求量 平均销售单价 周数6004010068 6 604 892.9939231 4 6004010116 32 153 703.7524386 22 6004010121 3 4 757.6972287 3 6004010134 3 4 1832.359083 3 6004010174 418 2601 1296.900566 113 6004010203 69 142 1016.392385 53 6004010205 44 93 1082.228075 24 6004010207 153 2064 962.1260938 80 6004010215 40 208 664.9324013 32 6004010217 48 189 942.9507148 34 6004010229 223 725 1221.654527 113……………6004100006 1 1 3500 1 6004100008 573 1223 1771.859329 151 6004100012 2 2 2917.111935 2

利用表4各个物料的总信息，以物料需求的频数、总需求量、平均销售单价和周频率为条件放入SPSS软件进行主成分分析，见表5.

KMO取样适切性量数 0.629巴特利特球形度检验 近似卡方 585.931自由度 6显著性 0

由表5可知，KMO 的值为0.629，大于阈值0.5，说明变量之间是存在相关性的，符合要求.巴特利特球形度检验结果中显著性为0 小于0.05，检验结果证明，这份数据是可以进行因子分析的.其相关矩阵的特征值及各主成分的贡献率，见表6.

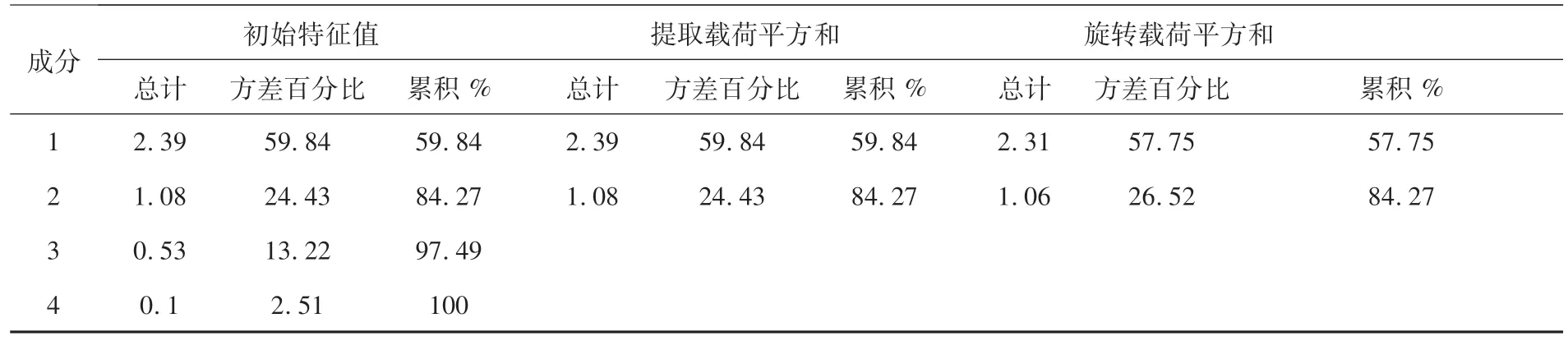
初始特征值 提取载荷平方和 旋转载荷平方和成分总计 方差百分比 累积% 总计 方差百分比 累积% 总计 方差百分比 累积%1 2.39 59.84 59.84 2.39 59.84 59.84 2.31 57.75 57.75 2 1.08 24.43 84.27 1.08 24.43 84.27 1.06 26.52 84.27 3 0.53 13.22 97.49 4 0.1 2.51 100

从表6中可以看出，前2个成分的累积贡献率为84.27%，大于80%.所以可以选取前2个成分作为主成分，并得到成分得分系数矩阵，见表7.

成分1 2频数 0.425 0.086总需求量 0.279－0.216平均销售单价 0.105 0.954周数 0.429 0.156

利用表7中所给的数据建立主成分表达式，计算出主成分得分F1、F2.

再以每个主成分的方差贡献率构造F1和F2的线性组合，得到主成分综合表达式，计算出主成分综合得分F.

计算得到284个物料的主成分得分、综合得分和排序见表8.

物料编码 F1 F2 F 排序6004020503 6.49 5.41 5.18 1 6004010256 4.04 4.44 3.51 2 6004020918 3.51 4.43 3.2 3 6004010174 3.16 3.41 2.73 4 6004021055 3.3 2.61 2.6 5 6004010252 3.54 1.7 2.5 6 6004020375 2.4 4.09 2.47 7 6004100008 2.17 3.83 2.27 8 6004020656 1.93 4.04 2.19 96004010286－0.97－0.74－0.75 283 6004010396－0.98－0.74－0.76 284

从表8的综合得分中选取出排序前6的物料为重点关注物料，编码分别是：6004020503、6004010256、6004020918、6004010174、6004021055和6004010252.

3 预测模型

3.1 模型构建

3.1.1 多元线性回归

多元线性回归模型［4］通常用来研究一个因变量依赖多个自变量的变化关系，多元线性回归模型可以用来描述物料需求和变量之间的随机线性关系，即：

其中，x1，…，xk是物料的变量；y 是物料的需求量；β0，…，βk是回归系数；ξ 是随机误差项.

3.1.2 逐步回归

逐步回归的基本思想：通过剔除物料信息中不太重要又和其他信息高度相关的物料信息，降低多重共线性程度.反复这个过程，直到既没有显著的信息选入回归方程，也没有不显著的信息从回归方程中剔除为止，以保证最后所得到的物料信息集是最优的.

3.1.3 BP 神经网络建立

BP神经网络［5］的结构对其性能有较大的影响，需对网络的结构和相关参数进行合理的设计.基于已知数据，选取sigmoid函数，函数公式

其中，x1，x2，…，xn为神经元的输入，输入一般为对系统模型关键影响的自变量.将信号结合输入到神经元有多种方式，选取最便捷的线性加权求和可得第h个隐藏层神经元的输入：

由于变量比较少，这里设置1 层隐藏层，进而得到第j个输出神经元：

其中，v，ω 分别为输入层到隐藏层，隐藏层到输入层的权重.通过已知的3 个因素，预测需要求解的1个因素，为更好的构建网络，需对隐藏层进行设计

其中，m 为输出神经元个数，n 为输入神经元个数，λ为常数，取值范围为1 ～5.计算得到S取值范围为2 ～7，设置1层隐藏层，其神经元个数为7，构建如图1所示的神经网络.

图1 神经网络基本架构

3.2 模型检验

3.2.1 多元线性回归

由于物料的需求量和频率、平均销售单价和总价应该是线性的关系.频率越高、平均销售单价越小，周总价越低，需求量就应该越大.因此以6个物料的频数、平均销售单价和周总价为自变量，需求量为因变量建立多元线性回归，得到物料回归方程的4个统计量，见表9.

R2 F p s2物料1 0.998 335679.65 0 0.0465物料2 0.9946 10765.37 0 0.4731物料3 0.9945 10490.17 0 1.0571物料4 0.9938 9243.91 0 3.5899物料5 0.9985 39184.71 0 1.2751物料6 0.9998 413422.87 0 1.3071

从表9中可以看出6种物料的判定系数R2都接近于1，p ＜0.0001，回归模型显著，并得到多元线性回归系数，见表10.

常数 频率 平均销售单价 周总价物料1 17.1518 0.0209－0.0772 0.0044物料2 0.1202 0.172－4.5636 0.0006物料3－0.0258 0.0256－2.7295 0.0004物料4 0.6927 0.3468－0.0002 0.0007物料5 0.4383－0.4053－0.0001 0.0009物料6 0.0519 0.2883－0.0001 0.0037

3.2.2 逐步回归

利用逐步回归通过剔除6 种物料中不太重要又和频率、平均销售单价、周总价3 个变量高度相关的数据，降低多重共线性程度.将6 种物料的3个变量的数据逐个引入模型，得到逐步回归系数，见表11.

常数 频率 平均销售单价 周总价物料1 17.1519 0.0209 0.0772 0.0044物料2 0.1203 0.172 0.0001 0.006物料3－0.1192 0.0004物料4 0.6927 0.3468 0.0002 0.0007物料5 0.4383－0.4053 0.0001 0.0009物料6 0.0303 0.0037

从表10和表11中可以看出，只有物料5的频率与需求量成负相关，其他都是正相关，频率越高，需求越大.所有的平均销售单价与需求量都成负相关，说明了物料的价格越高越难已销售，符合常理.

3.3.3 神经网络

通过1000次迭代，得到如图2所示的最佳性能验证图，最终迭代结果可以看出，BP 神经网络训练，验证和测试结果均趋于稳定，且最终平均方差均达到较小值，拟合程度到达最优.

图2 最佳性能验证图及迭代变化率

通过1000次的迭代，神经网络趋于收敛，最终迭代变化率为1.9582 ×10－6，获得最终结果.从图2曲线的前半部分之中也可以看出随着迭代次数的增加，网络通过训练其性能也在不断增加，误差逐渐降低.

通过对网络进行训练、验证以及测试，网络最终收敛到最佳性能状态.图3 为网络训练、验证、测试以及总的拟合系数图.网络训练、验证、测试的拟合系数为1，总的拟合系数为1，回归的情况较好.从而说明整体神经网络拟合理想，检验通过，可以用于数据预测.

图3 网络拟合系数

3.4 预测结果

分别以6个重点物料的频数、平均销售单价和周总价为训练集，需求量为输出集输入构建好的模型，得到预测的需求量值.以物料6004020503为例，3种模型的预测值与真实值对比图，残差如图4所示.

图4 物料6004020503预测对比图以及残差图

物料1 物料2 物料3 物料4 物料5 物料6 平均误差率多元线性回归 0.88% 5.58% 2.95% 7.87% 2.48% 0.85% 3.44%逐步回归 0.88% 5.58% 2.80% 7.87% 2.48% 0.93% 3.42%神经网络 0.63% 1.21% 1.06% 8.96% 0.35% 0.52% 2.12%

从表12中可以看出，

①对物料1、物料2、物料3、物料5和物料6来说BP 神经网络模型明显优于逐步回归、多元线性回归模型；

②对物料4来说BP神经网络模型的误差率8.96%略高于逐步回归、多元线性回归模型误差率（7.87%）；

③从整体和平均误差率上能看出，BP 神经网络模型最小（平均误差率：2.12%）优于其他2个模型，因此可以建立物料需求的神经网络周预测模型.

4 结论

综上，多品种小批量产品生产是一个既复杂又系统的生产过程，对企业生产管理有着很高的要求，这就需要不断加强生产计划安排，这样才能促使企业实现高质量发展.为更好的安排多品种小批量物料生产计划，先利用主成分分析，根据综合得分得到排名前6 的物料为重点关注物料（编码：6004020503、6004010256、6004020918、6004010174、6004021055、6004010252）.然后建立多元线性回归、逐步回归以及BP 神经网络3种预测模型，分别对6个重点关注物料需求量进行预测.综合预测结果，得到BP 神经网络为最优模型，其平均准确率为2.12%（见表12）.此方法能快速准确的为企业安排合理的生产计划，避免了生产过程中的库存与缺失，从而为企业创造更高的收益.