基于特征强化神经网络的交通流预测

李晓霞，石莹洁，祁昌平，林和

1. 河西学院 信息技术与传媒学院，甘肃 张掖 734000

2. 河海大学 水文水资源学院，江苏 南京 210098

3. 兰州大学 信息科学与工程学院，甘肃 兰州 730000

交通流量预测是该领域的热门研究课题，其研究在智能交通系统中具有重要意义[1]。交通流预测主要通过历史交通流时间序列数据预判路网未来的交通状况[2-3]，其结果可以为交通信息系统提供流量控制策略的基础数据，也可以直接用于先进交通管理系统的信息发布，为出行者提供实时有效的引导信息并帮助相关部门优化路径选择，是智能交通领域的关键性技术。因此，准确可靠的交通预测信息和交通流状态是路线引导系统的基础。

目前，交通流预测研究较多，主要集中于交通流序列的特征提取、预测模型的建立等领域。常用的预测方法包括平均、自回归滑动平均（autoregressive and moving average，ARMA）、线性回归、非参数回归[4-5]等方法。传统的统计模型如整合移动平均自回归（auto-regressive integrated moving average，ARIMA）模型[6]可以从交通数据中提取趋势特征，但是，ARIMA 等传统模型难以提取隐藏在交通数据中的非线性特征；而机器学习方法例如K 近邻（K-nearest neighbor，KNN）算法[7]和支持向量机（support vector machines，SVM）算法[8]虽然可以对更为复杂的数据进行建模，但是它们需要对特征进行工程处理，这意味着需要将原始数据转换为更适合模型使用的特征，即需要选择合适的特征集进行特征缩放和归一化等操作。因此，传统的统计模型的预测精度通常不能满足实际需求。

由于深度学习在语音识别和图像处理方面取得了突破，越来越多的研究人员将深度学习应用于时空数据预测，其可以结合非线性的模块来形成原始输入数据的多层次深度表示[9]。文献[10-11]也验证了深度学习优越的特征提取能力。大量研究发现，递归神经网络（recursive neural network，RNN）比反向传播（back propagation，BP）神经网络更能学习时间序列特征[12]，例如Sun 等[13]提出了一种新的基于门控递归单元的交通量预测模型，建立了一个优于其他递归神经网络的良好的城市交通量预测模型。总的来说，虽然上述深度学习算法提供了优秀的交通量建模能力，但对于关键信息的聚焦能力较弱。

为有效聚合多个节点的特征信息，提高模型对关键信息的聚焦能力以及分析和预测的效率，学者们将各个模型的优点结合在一起，提高预测性能。例如Li 等[14]提出了一种基于卷积神经网络（convolutional neural networks，CNN）结合长短时记忆网络(long short term memory，LSTM）的交通流预测新模型。实验结果表明，CNN-LSTM 能够建立良好的交通流预测模型。桂智明等[15]利用卷CNN 结合门控循环单元（gate recurrent unit,GRU）以及注意力机制构建新模型对交通流的周期性特征进行挖掘，对交通流进行预测，取得不错的预测效果。张龄允等[16]通过互补集成经验模态分解减少噪声对交通流数据预测的影响，采用CNN、LSTM 挖掘数据特征，预测性能相较于单一模型有较高的提升。Chen 等[17]提出了贝叶斯时间分解（Bayesian temporal factorization，BTF）模型，该模型可以在缺少时空数据的情况下预测交通流量。在该模型中，将张量分解和向量自回归的过程转换为图形结构，以减少数据丢失带来的不确定性，通过对几个真实时空数据集的验证，证明了BTF 模型优于现有方法。Wang 等[18]提出了一种多视图双向时空图网络，该模型用于预测缺少数据的城市交通流量。何鸿杰等[19]提出基于三次指数平滑法和深度残差网络的组合预测模型来预测交通流量，但模型计算成本较高。邴其春等[20]提出基于变分模态分解与长短时记忆神经网络的组合模型来预测短时交通流，预测精度有所提高。钟祥兴等[21]采用了基于变分模态分解-注意力机制-门控循环神经网络的组合预测模型，降低数据噪音，提高了预测精度。以上模型虽取得不错的预测效果，但只关注于对输入向量权重参数优化的情况下，模型预测中仍存在着挖掘特征能力不足的缺点。

因此本文提出一种基于特征强化的短时交通流预测模型——卷积神经网络-特征增强（feature enhancement，FE）-门控循环单元(CNN-FE-GRU）神经网络模型来预测交通网络中4 个路口中每个路口的交通流量，分析不同出行高峰例如工作日、周末以及节假日等交通特征，来解决挖掘特征能力不足的问题。

1 交通流预测模型

本文提出的CNN-FE-GRU 交通流预测模型设计思路如下：

1）利用CNN 对交通流时间序列进行特征提取，以捕捉交通流数据中的时空相关性。CNN 层可以有效地提取数据的空间特征，通过滑动窗口的方式对交通流时间序列进行卷积操作，提取出其空间特征。同时，通过池化层对特征进行降维，减少模型参数和计算量的同时保留数据信息。

2）使用FE 模块为数据赋予相应的特征权重值，对关键数据信息进行聚焦。FE 模块可以提高模型对关键数据信息的关注度，从而降低噪声对模型的影响。FE 模块可以根据特定的领域知识或者数据分布等特征，为数据赋予不同的权重值，从而使得模型更加关注与预测相关的数据信息。

3）通过GRU 对输出的时序数据再次提取时序数据特征的同时保证模型的效率，提高预测精度。GRU 层可以捕捉交通流数据中的时间序列特征，并且通过门控机制有效处理长序列数据，避免梯度消失和梯度爆炸问题。GRU 层可以将前一时刻的状态信息和当前时间步的输入信息结合起来，从而对时序数据进行建模和预测。

1.1 CNN-FE-GRU 模型网络架构

时间序列数据预测需要对关键数据信息进行聚焦，如果对于数据信息没有侧重点那么会导致模型学习效果降低。本文所提出的特征增强模块为不同的数据赋予不同的权重，旨在加强学习与目标有关数据的特征，降低对目标无关的数据特征，增强特征挖掘能力。

对于交通流预测问题，当给定交通流的时间序列数据S时，GRU 神经网络输出预测值Y。S由影响交通流的时间序列组成：

式中xt为t时刻的网络输入。

Y为需要预测的交通流量：

CNN 负责对输入的时间序列之间的潜在联系进行挖掘，GRU 负责对输出的时序数据进行选择性遗忘并保证模型的效率。C为含有权重的中间数据信息，计算方式为

式中：Wi为可学习的权重，hi为编码器隐含层输出。

当使用CNN 对时间序列的潜在特征进行提取后，本文利用FE 模块对处理后的数据赋予相应的权重，这样便进一步加强了模型的聚焦能力，因此特征增强模块需要对CNN 处理后的数据信息赋予不同的权重才能精准预测交通流。特征增强模块的权重计算时首先将输入的时间序列数据与经过CNN 处理后的数据进行对齐运算，得到对齐值si，对齐运算方式为

通过归一化指数函数softmax 将对齐值si进行特征增强得到增强后的权重 αt：

特征增强模块计算流程见图1。

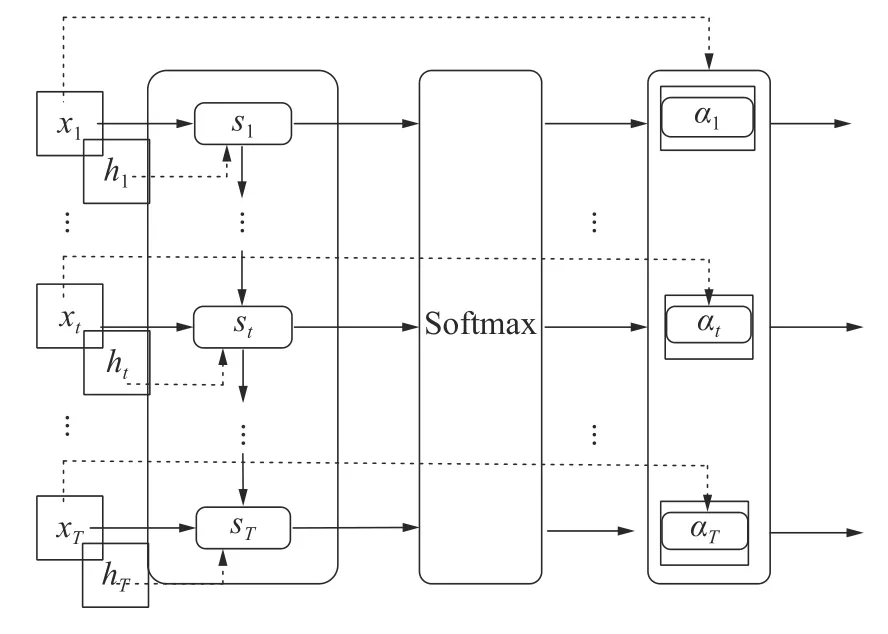
图1 FE 模块计算流程

交通流会随着时间在道路中不断地变化，本文提出的CNN-FE-GRU 模型采用CNN 神经网络对交通流进行预测。特征增强模块将CNN 的输出xt与隐含层状态ht进行对齐运算，然后通过softmax 函数将对齐后的结果映射至（0，1），得到αt。最终使用CNN 的输出xt与αt相乘，使得数据获得相应的权重。GRU 神经网络将处理含有特征权重的中间信息数据，其中，GRU 神经网络的复位门控制上一时刻隐藏层输出和当前时刻时间序列数据的输入，更新门控制上一时刻信息对当前时刻的影响程度，最后在GRU 神经网络和含有一个神经单元的全连接层作用下输出交通流数据。通过以上流程，整体提高了交通流预测性能，特征提取能力得到进一步的加强。模型整体结构见图2。

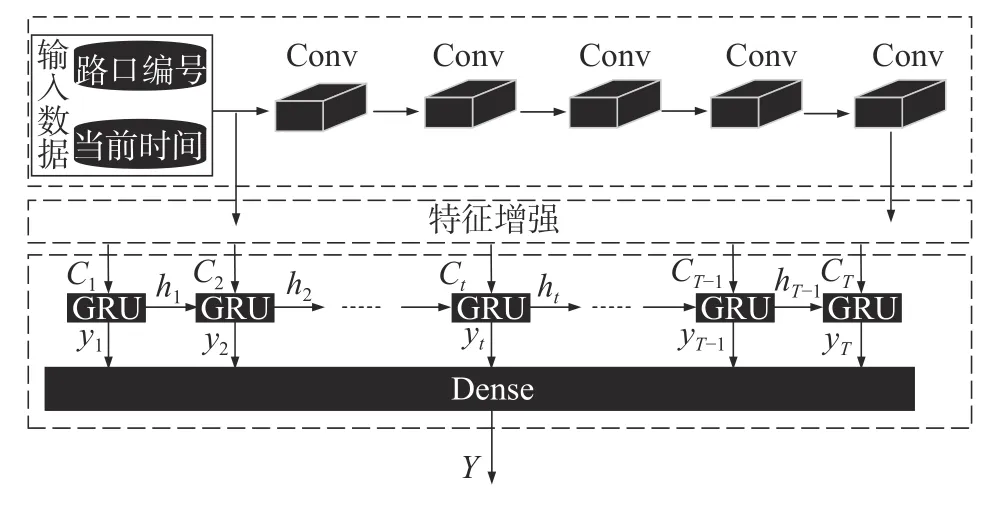
图2 CNN-FE-GRU 预测模型结构

1.2 CNN 模型

文献[22]的研究表明采用CNN 作为数据的输入层的预测模型效果更好。在预测应用中，可将CNN 分为输入部分、特征提取部分以及预测输出部分。CNN 层通过卷积操作进行局部趋势学习，对交通流的时间特征进行有效保留[23]。

CNN 利用卷积核对输入矩阵进行滤波，实现卷积运算。卷积层函数利用卷积核提取输入矩阵的特征信息：

式中：f为激活函数，为l层（i，j）位置的卷积滤波器对应的权重，为偏置，为前一层的特征映射，Mj为特征映射集，为当前层的特征映射。由于交通流数据具有非线性特征，所以选择ReLu 为激活函数，提高网络非线性特征学习能力。

1.3 GRU 模型

在交通流预测中历史交通流可能会对未来交通流量产生长期影响，存在长期依赖性特征，因此对交通流时间特征进行建模时，需对其长期依赖性进行考虑，CNN 可以解决RNN 中的长期依赖问题[24]。

GRU 中的更新门和重置门使其具有处理交通流的长期依赖特征的能力，因此对输出的时序数据进行再次特征提取的同时保证模型的效率，提高了预测精度。GRU 各门控计算过程如下：

式中：rt为复位门，zt为更新门，W为权重参数，为新的输入，为候选隐藏状态值，xt为t时刻的输入，ht-1为上一个时刻的隐藏状态，[ ]表示2 个状态值的组合，σ(·)为sigmoid 函数，tanh 为取值范围在[-1,1]的激活函数， ◦代表矩阵元素的哈达玛积。

2 实验设置

2.1 交通流预测问题描述

2.2 模型训练流程

以时间序列数据为输入，基于本文提出的CNN-FE-GRU 模型的实验流程如图3 所示。

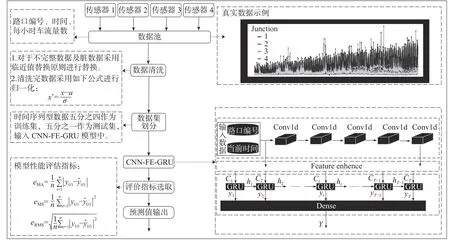
图3 CNN-FE-GRU 预测模型流程

1）数据收集及整理。对来源于INRIX 数据集收集的4 个路口的交通流量数据以及来源于PeMSD4 数据集的数据以时间序列形式整理，生成时间序列数据池。

2）数据处理。采用标准化的方式对数据进行去量纲化处理。

3）建立CNN-FE-GRU 模型。首先使用一维卷积神经网络挖掘路口、时间段与车流量的潜在联系，接下来使用特征增强模块增加模型聚焦能力，最后使用GRU 对输出的时序数据进行进一步的特征提取，完成对交通流量的预测。

4）模型预测误差计算。以平均绝对误差(mean absolute error，MAE)eMA、均方误差(meansquare error，MSE)eMS和均方根误差(root mean square error，RMSE)eRMS等误差函数对CNN-FEGRU 模型误差进行计算，通过训练使得模型能够更新网络层之间的参数，使得模型达到最优效果，当达到训练次数后模型停止训练。

5）真实数据模拟。为进一步展现CNN-FEGRU 模型预测性能，随机选取15 条真实数据并将真实数据特征值送入训练好的模型，将得到的预测值与真实数据中目标值进行对比，探究模型对于真实数据的模拟能力。

2.3 数据来源

本文选取了2 个数据集：一个数据集来源于INRIX，其为一家领先的网联汽车服务和交通分析解决方案提供商。该数据集包含了4 个路口数据，前3 个路口的数据为2015 年11 月1 日0 点—2017 年6 月30 日23 点的43 777 组逐时数据，第4 个路口的数据包含了2017 年1 月1 日0 点—2017 年6 月30 日23 点的4 344 组逐时数据。另一个数据集使用的是加利福尼亚州的高速公路交通数据集PeMSD4[25]，PeMSD4 数据集时间跨度为2018 年1—2 月，包含29 条道路上的3 848 个检测器。经过对数据清洗、筛选后去掉冗余探测器，确保相邻探测器距离大于5.6 km，最后剩余307 个探测器即307 个节点。

2.4 数据预处理

对模型训练时要对数据进行预处理，因为数据的类型不同，会有不同的单位及量纲，这样会影响交通流预测的精度，因此需通过数据标准化处理消除变量间存在的量纲关系。标准化公式为

式中：Vs为初始数据集值；Vmean为平均值；Vstd为标准差；V为标准化处理后的数据，用于输入到神经网络及其他模型中。

2.5 误差分析

为了比较不同模型的预测结果以及定量评价模型的预测性能，采用MAE、MSE 和RMSE 这3 个评价指标对实验模型真实值和预测值误差进行计算，误差函数具体计算方式为

式中：yˆ(t)为预测值，y(t)为实际值，n为样本数。最终得到的误差指标值越小，代表预测的结果越准确，预测效果越好。

2.6 模型参数设定

为了验证本文模型的有效性，进行了2 组实验。实验1 选取了4 个路口的数据，分为2015—2017 年的逐时数据和2017 年的逐时数据2 部分；实验2 选取了加利福尼亚州的高速公路交通数据集PeMSD4。

为了进行对比验证，实验1 的对照组模型包括了GRU 模型、CNN 模型、LSTM 模型和CNNGRU 模型。实验2 的对照组模型选取了历史平均方法(historical averaging，HA)、差分自回归滑动平均(autoregressive integrated moving average model，ARIMA)、向量自回归(vector autoregression，VAR)、图注意力网络（graph attention network，GAT）模型以及GAT-GRU 模型，并在此基础上添加了STGCN[26]和GeoMAN[27]模型。本文使用谷歌Tensorflow 开源平台搭建神经网络模型，并在搭载K80 显卡的Kaggle 平台进行模型训练。

实验1 和实验2 的基本参数设定大体相同，但是实验2 中批处理大小(batch size)设置为64，图注意力网络多头注意力头数为K=8，与文献[25]保持一致。具体来说，本文提出的CNN-FEGRU 模型参数设置如下：CNN 层的网络深度为32，卷积核大小均为2×2；全连接层的神经元个数为1，激活函数为Relu 函数；批处理大小为32。神经网络的基础参数如表1 所示。此外，文中还设置了学习率（learning rate，LR）RL来优化模型的训练效果。

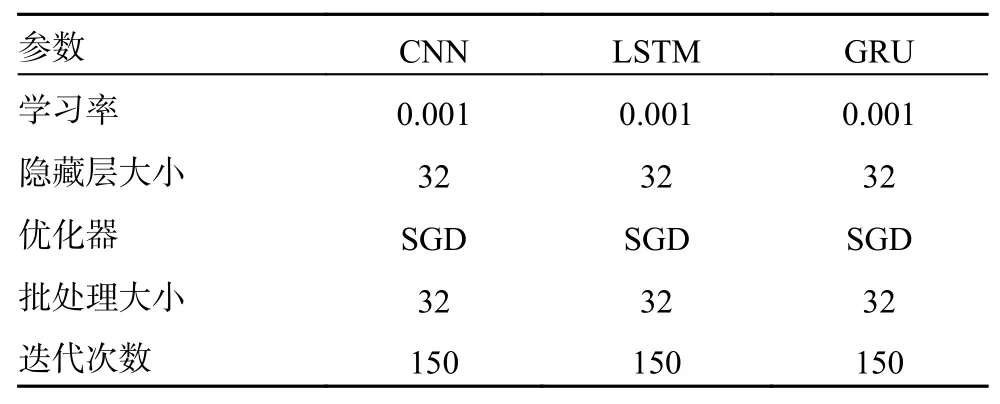
表1 实验基础参数表

2.7 模型性能评估

实验1 首先对4 个路口数据进行预测实验以评估CNN-FE-GRU 模型在交通流预测中的适用性，目的在于证明在数据量不同的情况下模型的预测精度是否仍然较高。模型的预测对比选取0—14 时逐时数据进行预测验证，如图4～图7所示，各模型的预测误差见表2。在路口1 的实验中，可以发现CNN-FE-GRU 模型相较于CNN模型、GRU 模型、LSTM 模型以及CNN-GRU 模型，MAE 分别下降了0.008 5、0.008、0.006 1、0.004 5，MSE 分别下降了0.005 9、0.004 4、0.004、0.003 1，RMSE 分别下降了0.113、0.010 7、0.008 8、0.005 4。而其他3 个路口的CNN-FE-GRU 模型相较于其他模型的误差值也是降低的。CNN-FE-GRU 模型在MAE、MSE 和RMSE 评价指标上的平均值分别为0.229、0.130 8、0.338 8。

表2 4 个路口的性能指标对比

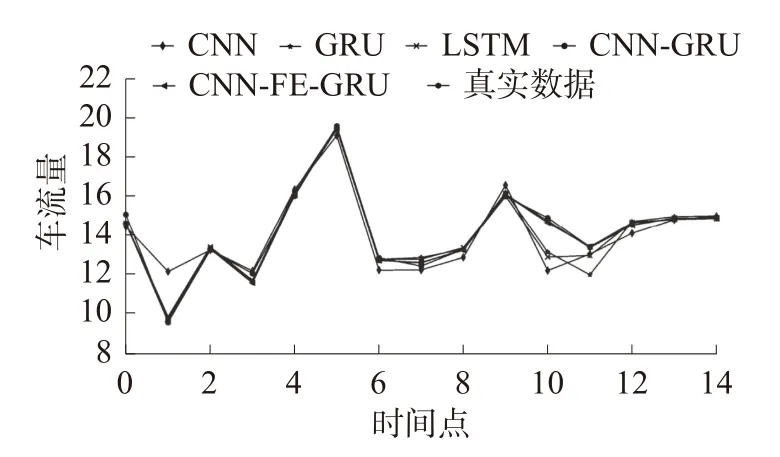
图4 路口1 预测

图5 路口2 预测

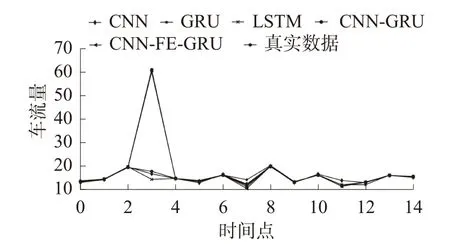
图6 路口3 预测

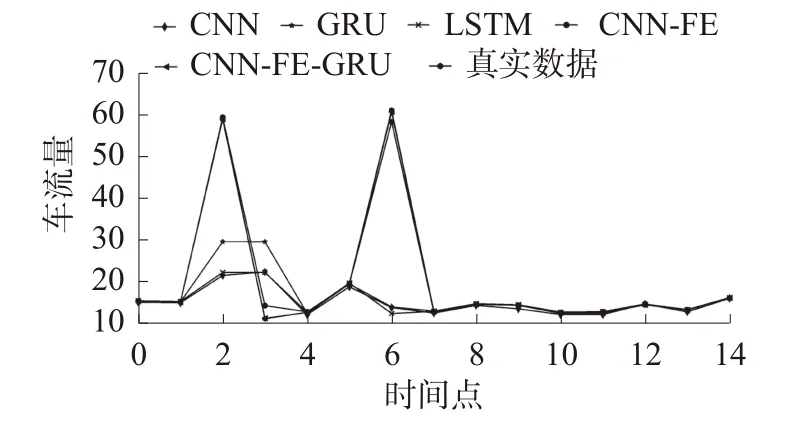
图7 路口4 预测

实验2 采用传统预测模型方法与本文提出的CNN-FE-GRU 模型进行横向的平均性能比较实验，为第4 个路口数据。实验结果如表3 所示，本文提出的CNN-FE-GRU 模型在MAE 和RMSE 评价指标上均有较为明显的下降。MAE 和RMSE分别为0.221 1 和0.351 7。在实验2 中，进一步验证了CNN-FE-GRU 模型在预测任务中的有效性，其预测误差也是最小的。

表3 第4 个路口性能指标对比

使用CNN-FE-GRU 模型进行交通流预测，在4 个不同路口的交通流预测任务中，CNN-FEGRU 模型在MAE、MSE 和RMSE 等指标上表现更优秀，比其他模型具有更高的预测精度。CNNFE-GRU 模型优越性在于其能够提取数据特征并聚焦关键数据信息，从而提高建模非线性和复杂的交通数据方面的能力，进而提高预测性能。实验结果表明CNN-FE-GRU 模型在数据量较大和较小的情况下都具有较高的预测精度和适应性。实验2 通过对传统预测模型的比对进一步证明CNN-FE-GRU 模型的优越性，表明其在面对不同交通流数据变化时模型预测稳定性更好，适用于复杂交通流预测的情形。

综上，CNN-FE-GRU 模型的优越性在于其能够发挥CNN 和GRU 这2 种模型的优点，并通过FE 模块提高建模能力，从而显著提高预测性能。

3 结论

1）本文结合CNN、FE 及GRU 的特点，提出了CNN-FE-GRU 模型。该模型在提取时间序列数据特征方面展现了较大的优越性，通过分析不同的出行高峰，有效提取不同的时间序列信息，减少数据冗余性，提高交通流量预测能力。

2）提出FE 方法，为不同时间下的特征赋予相应的权重，聚焦于对当前任务更为关键的信息，加强学习与目标有关数据的特征，降低对目标无关的数据特征。

3）使用INRIX 公司发布的4 个路口的真实数据集及加利福尼亚州的高速公路交通数据集PeMSD4 进行模拟实验，实验结果表明，与其他经典模型相比，添加了FE 模块的新算法在RMSE、MAE 等多种评价指标下，误差值与对比模型相比存在明显下降，说明了新算法的有效性。