浮式生产储卸油装置放空管路压力安全阀流致噪声特性
王义祥,安晨,张哲,刘畅,王振刚
1. 中国石油大学(北京) 安全与海洋工程学院,北京 102249
2. 南通中远海运船务工程有限公司,江苏 南通 226006
浮式生产储卸油装置(floating production storage offloading,FPSO)放空管路试运行阶段或紧急工况下,需通过压力安全阀(pressure safety valve,PSV)对管路系统的压力进行快速释放,内部的高速流体及其非稳定流动将诱发宽频流致噪声,进而对阀门下游管线产生振动和疲劳影响,引发泄漏等安全问题,造成生产停工和维修的经济损失[1-2]。压力安全阀是天然气管路系统中的重要元件,高速流体流经PSV 时,耗散的能量以机械能(阀门和管道的振动)、热能(流体温度变化)和声能(噪声)的形式传递到周围的环境中[3]。噪声沿管道向下游传播并沿圆周方向激励管壁,在非轴对称不连续焊缝处产生高动态应力,进而引起管道的高频振动和疲劳失效[4-5]。因此,研究压力安全阀流动特性及流致噪声特性对管线设计阶段判断并解决流致噪声问题具有重要意义。
国内外学者通过理论研究、数值模拟和实验手段,对减压装置内产生流致噪声的机理和特性进行了分析。理论研究的方法从控制方程出发,通过引入声类比理论或涡声理论等方法直接求解Navier-Stokes(N-S)方程,同时获得流场和声场的相关参数[6-7],理论方法求解较为复杂。数值模拟计算方法主要以Lighthill 声学类比理论为指导,并与计算流体力学(computational fluid dynamics,CFD)软件相结合,主要分为2 个步骤[8]:第一步通过湍流模型求解非定常流动特性[9-10],第二步采用有限元法、无限元法或边界元法求解声学波动方程[11]。目前采用较多的数值方法有2 种:一种为CFD 非定常模拟[12-13],即采用高级湍流模型精确地模拟出压力脉动,再结合声类比模型和快速傅里叶变换(fast Fourier transform,FFT)将时域上的结果转换到声压频域进行计算,可以实现定量分析噪声的频谱分布和总声压级,准确性高。另一种为CFD/计算气动声学(computational aeroacoustics,CAA)[14-15]方法。在CFD 非定常计算的基础上,将流场结果输入到SYSNOISE、ACTRAN等专业声学软件中求解远场的声压,计算声音的传播。与理论研究和数值模拟方法相比,实验方法最为直接,但实施困难,成本较高,相关实验研究较少。实验方法主要通过直接测量或间接测量来实现,直接测量即直接测量流致噪声;间接测量即为测量压力[16]、速度[17]和振动信号[18]等,然后建立这些参数与流致噪声的关系。
本文首先采用RNGk-ε模型结合宽频噪声模型进行稳态模拟,得到流体的速度、压力、声功率等参数特征,然后采用基于大涡模拟(large eddy simulation,LES)和Ffowcs Williams-Hawkings(FWH)的声类比方法对压力安全阀流致噪声进行瞬态模拟,得到远场噪声的频谱及指向性特性。
1 数值计算方法
1.1 大涡模拟法
本文采用大涡模拟数值方法模拟安全阀泄放过程的瞬态流场。大涡模拟根据漩涡的尺度将漩涡分为大尺度漩涡和小尺度漩涡2 种:大尺度涡流运动通过直接求解滤波后的N-S 方程得到;小尺度漩涡采用亚格子尺度(subgrid scale,SGS)模型进行模拟,连续性方程和过滤后的N-S 方程可以表示为
式中:xi和xj为物理坐标,和为流体速度在i、j方向的分量,t为时间,p为静压, ρ为密度, ν为动态黏度, τij为亚网格尺度应力:
亚网格尺度应力 τij是未知的, 采用Smagorinsky-Lilly 模型计算亚网格尺度应力:
式中: τkk是亚网格尺度应力的各向同性部分;δij为克罗内克符号; µt为亚网格尺度湍流黏度;为分解尺度的应变率张量,可表示为
在Smagorinsky-Lilly 模型中,亚网格尺度的湍流黏滞性计算公式为
式中:Ls为亚网格尺度下的长度;k为Von Karman常数,取值k=0.42;d为到最近壁面的距离;V是计算单元的体积;Cs为Smagorinsky 常数;
对于理想可压缩气体,其压力、密度和温度之间的关系定义为状态方程:
式中R为气体常数。
根据Nyquist 采样定理,时间步长 Δt应满足:
式中fmax为声学计算的最大频率。
为了保证数值计算的准确性和稳定性,需使库朗数Co小于1,即
式中: Δx为流动方向单元大小,U为通过单元的流速。
此外,需要计算的总时长T由声学频率的分辨率 Δf决定:
1.2 FW-H 声学类比模型
本文采用基于Lighthill 声学类比理论的FWH 模型计算安全阀流致噪声辐射特性,FW-H 方程是一个非齐次波动方程,依照Lighthill 的推导步骤,将连续性方程和动量方程整理为含有2 个面源和1 个体源的有源波动方程,即FW-H 方程。同时结合Kirchhoff 可渗透表面积分法得到远场解。远场辐射声压中包含厚度噪声、负荷噪声以及四极子噪声,详细的公式推导以及公式中符号含义和公式表达的物理意义见文献[19]。
2 数值模型及网格划分
2.1 边界条件和网格划分
压力安全阀在紧急泄放工况下会产生严重的流致噪声,并对下游管壁形成激励作用,建立压力安全阀三维结构模型,并将其导入ANSYS Design Modeler 模块中。由于阀体内表面几何模型复杂,采用Fill 命令中的By Gaps 方法提取压力安全阀100%开度下的流体域并进行修复和简化,如图1 所示。

图1 压力安全阀几何模型及流体域提取示意
由于压力安全阀的流体域复杂,故采用十二面体网格对流体域进行网格划分。在近壁面给流体域添加边界层网格,大涡模拟壁面网格要求和增强壁面函数一致,要求y+取值为1[20],通过计算求得第一层边界层网格的高度Δy=0.05mm,边界层层数为10 层,增长率为1.2,生成的十二面体网格如图2 所示。

图2 流体域十二面体网格
为了避免网格质量等因素对数值计算结果造成影响,选择6 种不同的网格尺寸对压力安全阀流体域进行网格划分,网格无关性验证数据如表1所示。

表1 网格无关性验证
结果表明,网格数大于898 132 时,监测点的声压级的变化较小。综合考虑仿真的准确性和计算时间,采用总网格数为1 045 253 的划分方案,面网格最大尺寸为2 mm,体网格最大尺寸为3 mm。
将流体介质设置成理想可压缩气体,入口压力为11 MPa,出口压力为2 MPa。采用密度基求解器,选择隐式求解方法,稳态求解控制残差设置为10-4,瞬态求解时间步长10-4s,数值仿真的流动过程时间为0~2 s。
2.2 数值方法可靠性验证
采用美国西南研究院[21]天然气管线流致噪声全尺寸实验测试作为验证算例,其实验测试装置如图3 所示。该实验将1 个7.62 cm×10.16 cm 压力安全阀作为噪声源的输入,在安全阀下游0.25 m 处进行噪声的监测,本节建立与实验相同的安全阀模型,根据该实验装置的入口压力、出口压力、质量流量和温度等边界条件,采用非定常LES 结合FW-H 声学模型的数值模拟方法进行计算。

图3 美国西南研究院实验测试回路
对比结果如表2 所示:阀门出口质量流量为31.334 kg/s,实验测量值为32 kg/s,误差为2.081%;在安全阀下游0.25 m 处的总声压级为145.99 dB,实验测得150 dB,误差为2.673%,误差均小于5%,证明了本文采用的数值模拟方法的可靠性。

表2 模拟结果和实验结果对比
3 压力安全阀流动特性分析
3.1 压力和速度分布
采用RNGk-ε模型进行稳态流场计算,压力和速度云图如图4 和图5 所示。结果表明,流体在节流段、阀门内腔和出口段经历3 次压降,节流段出现最大压降4.55 MPa,流体进入阀门内腔迅速膨胀,流速峰值达581.2 m/s,出现超音速流动,高压降导致的非稳定流动是流致噪声的根本原因。

图4 压力安全阀z=0 截面压力云图

图5 压力安全阀z=0 截面速度云图
3.2 涡结构分布
采用大涡模拟进行瞬态流场求解,通过Q准则进行涡量计算,结果如图6 所示。在图中5 个位置产生了明显的涡结构,此时刻的速度矢量图如图6(d)所示,在1~4 这4 个位置产生了速度漩涡,导致了涡的产生;在位置5 处,Q的绝对值较大,这是由于在此处不稳定剪切层从壁面脱落发生分离,逐渐形成强烈的大涡结构。

图6 压力安全阀z=0 截面涡结构Q 值云图
4 压力安全阀流致噪声特性分析
4.1 噪声产生位置及原因分析
由于阀门的复杂结构导致内部流体流动非常复杂,因此噪声源的种类和位置分布也不具有单一性,下面进一步剖析噪声产生的位置及原因。
1)偶极子声源。基于稳态计算结果,利用宽频噪声模型得到阀门声功率分布情况,声功率级最大值174 dB,严重超过可接受的155 dB。流体在图7 所示压力安全阀中的5 个位置高速撞击壁面,与壁面耦合产生强烈的脉动压力,对应图8 所示的带状和环状高声功率区域为偶极子声源,是面声源。

图7 压力安全阀z=0 截面速度流线图

图8 压力安全阀壁面声功率云图
2)四极子声源。根据图6 截面Q值云图可知,由于湍流的作用,在图中的5 个位置形成四极子声源,为体声源。由图9 可知,四极子体声源在阀门内部作用后的声功率最大值为110 dB,其强度和壁面偶极子声源相比来说影响较小。因此,偶极子面声源占据主导地位。

图9 压力安全阀截面声功率云图
单极子声源由表面加速度或位移引起,压力安全阀的流致噪声模拟中,将阀门内壁面视为刚性壁面,因此可以忽略不计。综上所述,安全阀泄放过程中的气动噪声是偶极子声源与四极子声源共同作用的结果,且偶极子面声源占据主导地位。
4.2 噪声频谱特性和指向性分析
将阀门作为噪声的输入源,采用基于FWH 方程的声类比积分方法,对阀门流致噪声进行瞬态模拟,定义如图10 所示的接收点,通过FFT对接收点的声压信号进行处理,得到远场噪声的频谱特性及其指向性。
图11为出口轴线方向接收点的1/3 倍频曲线,曲线具有相同的分布规律,接收点的声压级整体趋势随着频率的增加先增加后降低。由图12 功率谱密度图可以看出,噪声显示出的特性为宽频,主要集中在500~2 000 Hz。

图11 出口轴线方向接收点噪声1/3 倍频曲线

图12 接收点的功率谱密度
用接收点的总声压级表征噪声的指向性,以R=2 m 圆上的接收点总声压级数据为例,可以明显观察到不同开启高度(图13)和不同入口压力下(图14)的总声压级均在φ=120°方向附近达到最大值。不同入口压力下阀门出口轴线方向各接收点的总声压级如图15 所示,在距离阀门出口0~0.5 m 处,总声压级衰减最快,下降了23.851 dB;距离阀门出口1~3 m 处,总声压级衰减趋缓,平均每米衰减14.2 dB。
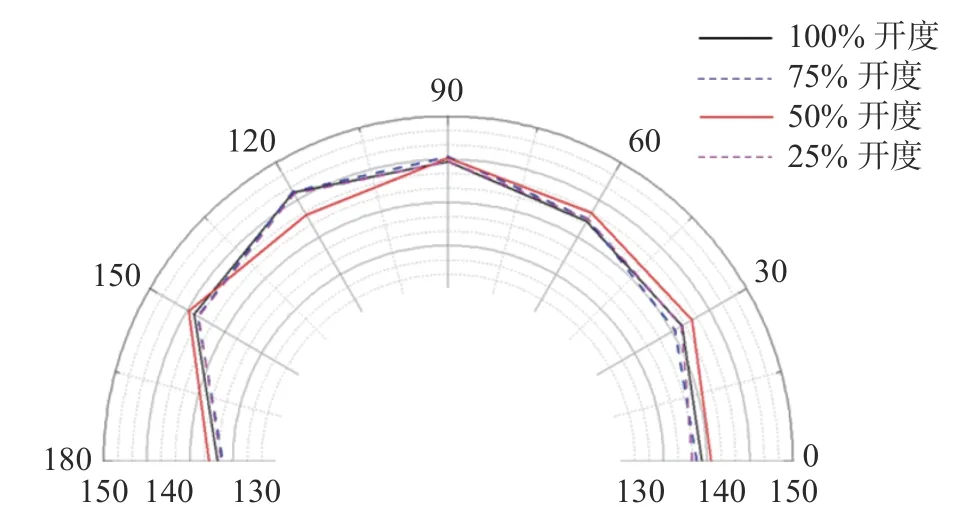
图13 不同开启高度下噪声指向性分析

图14 不同入口压力下噪声指向性分析

图15 不同入口压力下阀门出口轴线方向各接收点的总声压级
4.3 开启高度对噪声源的影响
不同开启高度会使安全阀内的流道发生改变,进而对流体的流动产生直接影响,导致流致噪声的变化。为了研究阀门开启高度对内部流场和噪声的影响规律,建立了压力安全阀开启高度分别为20 mm(100%)、15 mm(75%)、10 mm(50%)、5 mm(25%)工况下的数值模型,入口压力和出口压力等边界条件均保持一致。
首先对偶极子声源位置进行对比分析。由图16 可知,4 个工况在侧壁面下方的带状高声功率区域较为明显,位置基本一致,宽度随开度减小而减小,左侧上方的速度漩涡在在25%、50%开度工况不明显,导致侧壁面上方和阀瓣壁面带状高声功率区域不明显,即强度较低。由图17可知,随着开度的减小,阀瓣下表面环状高声功率区域面积减小,且向下表面外边缘方向衰减。100%工况的最大声功率级为174 dB,75%工况的最大声功率级为170 dB,50%工况的最大声功率级为168 dB,25%工况的最大声功率级为166 dB,由此可知,壁面最大声功率级随着开度的增大而增大。

图16 不同开启高度下安全阀外壁面声功率云图

图17 不同开启高度下安全阀阀瓣下表面声功率云图
四极子声源主要是由湍流导致的,为体声源,图18 显示的为不同开启高度工况的涡量图。对不同开启高度下的四极子声源位置进行对比可知,4 种工况下涡结构的主要在图18 中的5 个位置产生,不同开启高度下涡结构的分布位置较为相似。开启高度为5 mm 工况下,在1、2 位置产生的涡结构Q值明显小于其他3 种工况,主要由于5 mm 为微启状态,流通通道相对较小,流体进入内腔膨胀减弱导致。

图18 不同开启高度下Q 值云图
5 结论
本文针对某型压力安全阀,围绕气体流致噪声问题,分析了压力安全阀在紧急泄放工况下的流场分布特性和流致噪声特性。得出结论如下:
1)安全阀内部噪声主要是由于高压降引起的超音速流动导致的,且流致噪声类别有2 种,一种是由于流体高速撞击壁面引起压力扰动而产生的偶极子面声源,另一种由于湍流引起的四极子体声源,其中偶极子声源占据主导地位。
2)噪声的频率主要集中在500~2 000 Hz,在与出口轴线夹角为120°方向附近声压级最高,总声压级沿出口轴线方向衰减,且在0~0.5 m 衰减最快。
3)随着开启高度的增大,壁面最大声功率级逐渐增大,偶极子声源产生位置随之发生明显改变,四极子声源位置不变。

