固定围长与最大度的单圈图的Wiener指数

武军秀, 高玉斌

(中北大学数学学院, 山西 太原 030051)

0 引言

1947年,化学家Wiener提出了Wiener指数。目前,Wiener指数已取得了许多的研究成果。学者们不仅在特定图类如单圈图、树图、双圈图中刻画了Wiener指数的极图;还在固定围长、最大度、最小度、悬挂点数等条件下刻画了Wiener指数的极图[6-10]。Chen H L等[7]提出了关于刻画固定围长和最大度的n阶图类中Wiener指数的极小图的问题。为解决该问题,本文中从围长与最大度均为3的单圈图类入手,得到了此类图Wiener指数的极小图的一些结构性质。

1 引理

引理1.1[5]固定最大度的树图中,T∈T(Δ,Δ)为最小Wiener指数图。

推论1.3设U′是U(3,3)中具有极小Wiener指数的图,则U′∈U(T1,T2,T3)。

推论1.3的证明设U∈U(3,3),其圈上的顶点为vi(i=1,2,3),Ti为U在vi的分支,则至少存在一点vi使得d(vi)=3,根据引理1.1～1.2,经过图变换,使得度为3的顶点vi所在的分支变为顶点数相同的Ti′∈T(1,3)时其Wiener指数变小,得证。

引理1.4[12]设G1,G2分别为n1,n2阶连通图,u∈V(G1),v∈V(G2),若G是通过粘合u,v两点构成的图,则W(G)=W(G1)+W(G2)+(|V(G2)|-1)D(u|G1)+(|V(G1)|-1)D(v|G2)。

引理1.5设a1,b1,c,d为任意正整数,满足a1≤b1,则

得证。

2 准备工作

设U∈U(T1,T2,T3),v1,v2,v3∈V(C3),Ti是U在vi点的分支,记Ti的顶点数为ni(n=n1+n2+n3,n≥13),层数为ki,第ki层的顶点数为mi,满足k2≥k1≥k3>0。选取分支T2,T3,讨论图变换对Wiener指数的影响。

2.1 图变换设w为T2中第(k2-1)层最上边的顶点,u,u1为T2中第k2层与w相邻的顶点。若m3=2k3-1,则w1为T3中第k3层最上边的顶点,d(w,w1)=k2+k3;若1≤m3≤2k3-1-1,则w1为T3中第(k3-1)层最上边的顶点,d(w,w1)=k2+k3-1。令U1=U-uw+w1u,G=U-u,Ti中第ki层的顶点构成集合Vi,T′i=Ti-Vi。

利用引理1.4易知,W(U)-W(U1)将等于图G中所有顶点到w,w1两点距离差的总和。

G中顶点到w,w1两点的所有可能的距离差:

1)T1中顶点到w,w1两点的距离差为k2-1-d(v3,w1)。

2)T2-u中顶点到w,w1两点的距离差:

-d(w,w1), 2-d(w,w1), 4-d(w,w1),…,2i-d(w,w1),i=1,2,…k2-1.

3)T3中顶点到w,w1两点的距离差:

d(w,w1),d(w,w1)-2,d(w,w1)-4,…,d(w,w1)-2i,i=1,2,…d(v3,w1).

各个距离差所对应的点数:

1)T1中距离差为k2-1-d(v3,w1)的点数为n1。

2)T2-u中各个距离差所对应的点数。距离差为2(k2-1)-d(w,w1)的点数为1,即v2点;若m2≠1,则距离差为-d(w,w1)的点数为1,即u1点;距离差2i-d(w,w1)(i=1,2,…,k2-2)所对应的点数可通过图U(如图1)的特点而获得。如下:

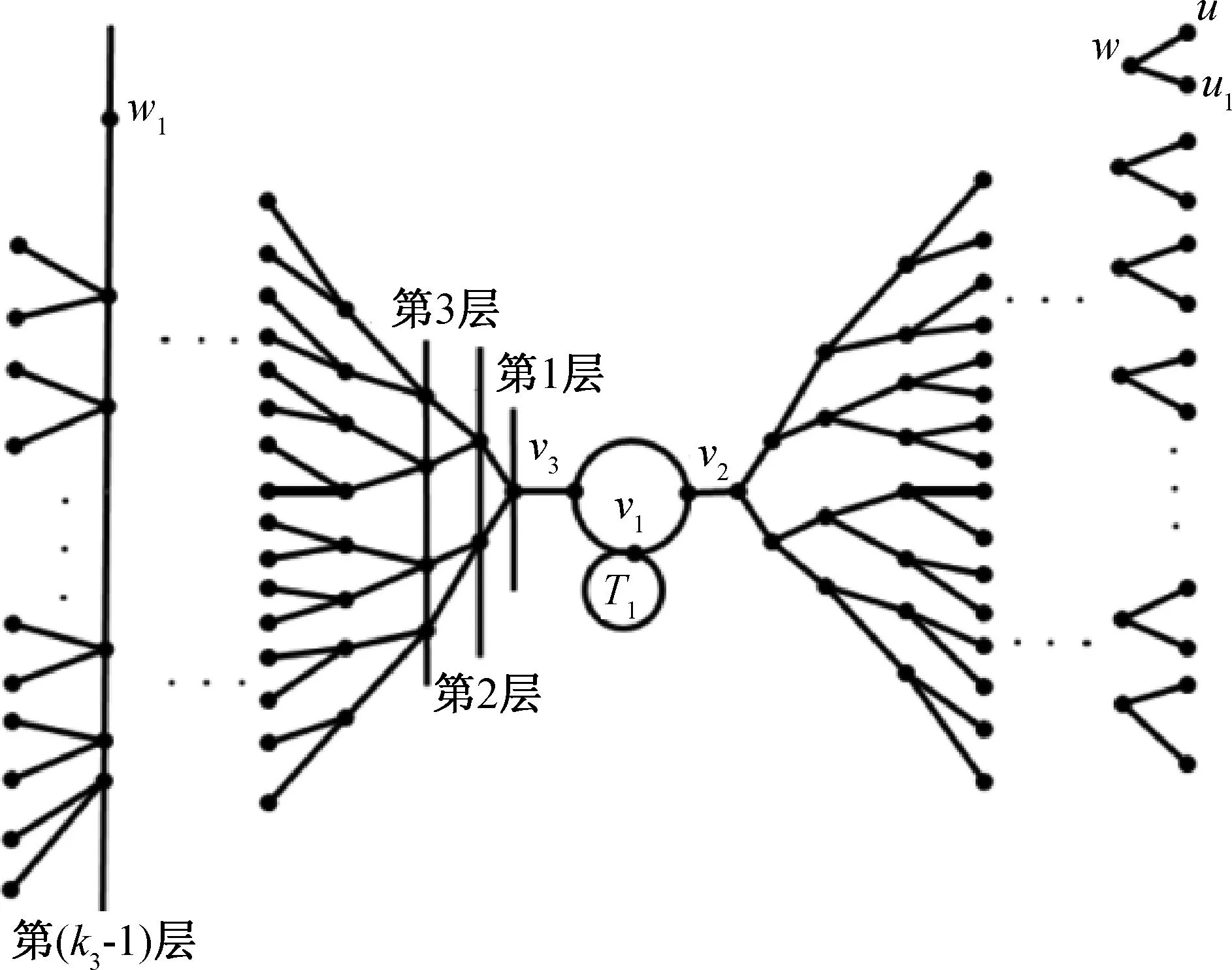
图1 图U

距离差2i-d(w,w1)(i=1,2,…,k2-2)在T′2中所对应的点数为2i。

若m2=1或2,则距离差2i-d(w,w1)(i=1,2,…,k2-2)在T2-u中所对应的点数为2i。

若m2≥3,且2l+1≤m2≤2l+1(1≤l≤k2-2),则第k2层中,距离差2i-d(w,w1)(i=1,2,…,l-1)的点数为2i,距离差2l-d(w,w1)的点数为m2-2l;2i-d(w,w1)(i=l+1,…k2-2)的点数为0。

若m2≥3,且2l+1≤m2≤2l+1(1≤l≤k2-2),则T2-u中距离差2i-d(w,w1)(i=1,2,…l-1)的点数为2i+1,距离差2l-d(w,w1)的点数为m2,距离差2i-d(w,w1)(i=l+1,…k2-2)的点数为2i。

3)T3中各个距离差所对应的点数。距离差为d(w,w1)-2d(v3,w1)的点数为1,即v3点;若m3=2k3-1-1,则距离差为d(w,w1)的点数为1,即第k3层与w1相邻的顶点;距离差d(w,w1)-2i(i=1,2,…,d(v3,w1)-1)所对应的点数可通过图U的特点而获得。如下:

若m3=2k3-1,则距离差d(w,w1)-2i(i=1,2,…,d(v3,w1)-1)在T3中所对应的点数为2i。

若1≤m3≤2k3-1-1,则距离差d(w,w1)-2i(i=1,2,…d(v3,w1)-1)在T3′中所对应的点数为2i。

若1≤m3≤2k3-2,则第k3层中,距离差d(w,w1)-2(d(v3,w1)-1)的点数为m3,距离差d(w,w1)-2i(i=1,2,…,d(v3,w1)-2)的点数为0。

若2k3-1-2k3-r-1

2.2 Wiener指数值的变化在k2-k3≥2的条件下,可分为两种情形:

情形1:m3=2k3-1。

情形1.1:m2=1。

情形1.2:m2=2。

W(U)-W(U1)=D(w|G)-D(w1|G)

(k2-k3)+(k2-k3-2)-(k2+k3)

=2k2-1(k2-k3-6)+2k3(k2-k3+4)+2(k2-k3)-2+n1(k2-k3-1)-(k2+k3).

情形1.3:2l+1≤m2≤2l+1(1≤l≤k2-2).

若1≤l≤k3-1,利用引理1.5,则

W(U)-W(U1)=D(w|G)-D(w1|G)

n1(k2-k3-1)+2(k2-k3)-2-(k2+k3)

=2k2-1(k2-k3-6)+2k3(k2-k3+4)+n1(k2-k3-1)+2(k2-k3)-2-

(m2-1)(k2+k3)+2(2+m2l-2l+1).

若k3≤l≤k2-2,利用引理1.5,则

W(U)-W(U1)=D(w|G)-D(w1|G)

=2k2-1(k2-k3-6)+2k3(k2-k3+4)+n1(k2-k3-1)+2(k2-k3)-2-

(m2-1)(k2+k3)+2(2+m2l-2l+1).

综上所述,若1≤l≤k2-2,则

W(U)-W(U1)=2k2-1(k2-k3-6)+2k3(k2-k3+4)+n1(k2-k3-1)

+2(k2-k3)-2-(m2-1)(k2+k3)+2(2+m2l-2l+1)

(1)

特别地,m2=1,2(l=0)时也满足(1)式。

情形2:1≤m3≤2k3-1-1。

若1≤m3≤2k3-2,则第k3层上点的距离差之和为m3(k2-k3+3);若2k3-1-2k3-r-1

2k3-2(k2-k3+3)+…+2k3-r-1(k2-k3+2r+1)+(m3-(2k3-1-2k3-r-1))(k2-k3+2r+3)

=2k3(1-r)-2k3-r+m3(k2-k3+2r+3)≥2k3(1-r)-2k3-r+(2k3-1-2k3-r-1)(k2-k3+2r+3)

=2k3-1(k2-k3+5)-2k3-r-1(k2-k3+2r+5)

≥2k3-2(k2-k3+3)

>0.

综上,若2l+1≤m2≤2l+1(1≤l≤k2-2)或m2=1,2(l=0),则

(2)

3 主要结论

定理1设U*是U(3,3)中具有极小Wiener指数的图,阶数n≥13,其各个分支的层数满足k2≥k1≥k3>0,则

1)若m3=2k3-1,m2=1,则k2-k3≤5。

2)若m3=2k3-1,2k2-2

3)若m3=2k3-1,2≤m2≤2k2-2,则k2-k3≤6。

定理1的证明记图变换后的图为U1。易知n1≥2k3。令m2=1,若k2-k3≥6,则代入(1)式得

W(U*)-W(U1)=2k2-1(k2-k3-6)+2k3(k2-k3+4)+n1(k2-k3-1)+2(k2-k3)-2

>0,

结果(1)得证。

令m2=2k2-q+a(2≤q≤k2,1≤a≤2k2-q),l=k2-q,代入(1)式,

W(U*)-W(U1)=2k2-1(k2-k3-6)+2k3(k2-k3+4)+n1(k2-k3-1)+2(k2-k3)-2-

(2k2-q+a-1)(k2+k3)+4+2k2-q+1(k2-q-2)+2a(k2-q)

=2k2-q(2q-1(k2-k3-6)+(k2-k3)-2q-4)+2k3(k2-k3+4)+

n1(k2-k3-1)+a(k2-k3-2q)+3k2-k3+2

(3)

若k2-k3≥2q,则由(3)式得

W(U*)-W(U1)≥2k2-q(2q-1(k2-k3-6)+(k2-k3)-2q-4)+

2k3(k2-k3+4)+n1(k2-k3-1)+3k2-k3+2

(4)

若k2-k3≥2q+2,则f(q)=2k2-q(k2-k3-2q-4)单调递减;若2q≤k2-k3≤2q+1,则f(q)单调递增。

若k2-k3≤2q-1,则由(3)式得

W(U*)-W(U1)≥2k2-q(2q-1(k2-k3-6)+(k2-k3)-2q-4+(k2-k3)-2q)+

2k3(k2-k3+4)+n1(k2-k3-1)+3k2-k3+2

=2k2-q(2q-1(k2-k3-6)+2(k2-k3)-4q-4)+2k3(k2-k3+4)+

n1(k2-k3-1)+3k2-k3+2

(5)

若k2-k3≤2q-1,则f(q)=2k2-q(2k2-2k3-4q-4)单调递增。

情形1:q=2。

若k2-k3≥6=2q+2>4=2q,则由(4)式得

W(U*)-W(U1)≥2k2-1(k2-k3-6)-(k2+k3)-4+2k3(k2-k3+4)+

n1(k2-k3-1)+3k2-k3+2

≥2k3(2k2-k3-1(k2-k3-6)+2(k2-k3)+3)+2(k2-k3-1)

>0

(6)

结果(2)得证。

情形2:3≤q≤k2。

情形2.1:q=3。

若k2-k3≥8=2q+2>6=2q,则由(6)式可知,W(U*)-W(U1)>0。

若k2-k3=7=2q+1>6=2q,则由(4)式得

W(U*)-W(U1)≥2k2-1(k2-k3-6)+2k2-3(k2-k3-10)+2k3(k2-k3+4)+

n1(k2-k3-1)+3k2-k3+2

>2k3(2k2-k3-3(5k2-5k3-34)+2(k2-k3)+3)>0

(7)

情形2.2:4≤q≤k2。

若k2-k3≥2q+2≥10,则由(6)式可知,W(U*)-W(U1)>0。

若k2-k3=2q+1≥9,则由(7)式可知,W(U*)-W(U1)>0。

若k2-k3=2q≥8,则由(4)式得

W(U*)-W(U1)≥2k2-1(k2-k3-6)+2k2-4(k2-k3-12)+2k3(k2-k3+4)+

n1(k2-k3-1)+3k2-k3+2

>2k3(2k2-k3-4(9k2-9k3-60)+2(k2-k3)+3)>0。

若7≤k2-k3≤2q-1,则由(5)式得

W(U*)-W(U1)≥2k2-1(k2-k3-6)+2k2-3(k2-k3-10)+2k3(k2-k3+4)+

n1(k2-k3-1)+3k2-k3+2

>2k3(2k2-k3-3(5k2-5k3-34)+2(k2-k3)+3)>0.

结果(3)得证。

证毕。

定理2设U*是U(3,3)中具有极小Wiener指数的图,阶数n≥13,其各个分支的层数满足k2≥k1≥k3>0,则

1)若1≤m3≤2k3-1-1,m2=1,则k2-k3≤4。

2)若1≤m3≤2k3-1-1,2k2-2

3)若1≤m3≤2k3-1-1,2≤m2≤2k2-2,则k2-k3≤5。

定理2的证明记图变换后的图为U1。易知n1≥2k3。令m2=1,若k2-k3≥5,则代入(2)式得

W(U*)-W(U1)≥2k2-1(k2-k3-5)+2k3-1(k2-k3+5)+2(k2-k3)+m3(k2-k3+3)+n1(k2-k3)>0。

结果(1)得证。

令m2=2k2-q+a(2≤q≤k2,1≤a≤2k2-q),l=k2-q,代入(2)式,

W(U*)-W(U1)

≥2k2-1(k2-k3-5)+2k3-1(k2-k3+5)-(2k2-q+a-1)(k2+k3-1)+

4+2k2-q+1(k2-q-2)+2a(k2-q)+2(k2-k3)+m3(k2-k3+3)+n1(k2-k3)

=2k2-q(2q-1(k2-k3-5)+(k2-k3)-2q-3)+2k3-1(k2-k3+5)+n1(k2-k3)+

a(k2-k3+1-2q)+(m3+1)(k2-k3)+2k2+3(m3+1)

(8)

若k2-k3≥2q-1,则由(8)式得

W(U*)-W(U1)≥2k2-q(2q-1(k2-k3-5)+(k2-k3)-2q-3)+2k3-1(k2-k3+5)+

n1(k2-k3)+(m3+1)(k2-k3)+2k2+3(m3+1)

(9)

若k2-k3≥2q+1,则f(q)=2k2-q(k2-k3-2q-3)单调递减;若2q-1≤k2-k3≤2q,则f(q)单调递增。

若k2-k3≤2q-2。则由(8)式得

W(U*)-W(U1)≥2k2-q(2q-1(k2-k3-5)+(k2-k3)-2q-3+k2-k3+1-2q)+

2k3-1(k2-k3+5)+n1(k2-k3)+(m3+1)(k2-k3)+2k2+3(m3+1)

=2k2-q(2q-1(k2-k3-5)+2(k2-k3)-4q-2)+2k3-1(k2-k3+5)+

n1(k2-k3)+(m3+1)(k2-k3)+2k2+3(m3+1)

(10)

若k2-k3≤2q-2,则f(q)=2k2-q(2k2-2k3-4q-2)单调递增。

情形1:q=2。

若k2-k3≥5=2q+1>3=2q-1,则由(9)式得

W(U*)-W(U1)≥2k2-1(k2-k3-5)-(k2+k3)-3+2k3-1(k2-k3+5)+n1(k2-k3)+

(m3+1)(k2-k3)+2k2+3(m3+1)

>2k3-1(2k2-k3(k2-k3-5)+3(k2-k3)+5)+3(k2-k3+1)>0

(11)

结果(2)得证。

情形2:3≤q≤k2。

情形2.1:q=3。

若k2-k3≥7=2q+1>5=2q-1,则由(11)式可知,W(U*)-W(U1)>0。

若k2-k3=6=2q>5=2q-1,则由(9)式,得

W(U*)-W(U1)≥2k2-1(k2-k3-5)+2k2-3(k2-k3-9)+2k3-1(k2-k3+5)+n1(k2-k3)+

(m3+1)(k2-k3)+2k2+3(m3+1)

>2k3-1(2k2-k3-2(5k2-5k3-29)+3(k2-k3)+5)>0

(12)

情形2.2:4≤q≤k2。

若k2-k3≥2q+1≥9,则由(11)式可知,W(U*)-W(U1)>0。

若k2-k3=2q≥8,则由(12)式可知,W(U*)-W(U1)>0。

若k2-k3=2q-1≥7,则由(9)式得

W(U*)-W(U1)≥2k2-1(k2-k3-5)+2k2-4(k2-k3-11)+2k3-1(k2-k3+5)+

n1(k2-k3)+(m3+1)(k2-k3)+2k2+3(m3+1)

>2k3-1(2k2-k3-3(9k2-9k3-51)+3(k2-k3)+5)>0.

若6≤k2-k3≤2q-2,则由(10)式得

W(U*)-W(U1)≥2k2-1(k2-k3-5)+2k2-3(k2-k3-9)+2k3-1(k2-k3+5)+

n1(k2-k3)+(m3+1)(k2-k3)+2k2+3(m3+1)

>2k3-1(2k2-k3-2(5k2-5k3-29)+3(k2-k3)+5)>0.

结果(3)得证。

证毕。