基于半偏联系数和动态差异度系数的区域旱灾风险评估方法

陈浩, 金菊良,2, 崔毅,2, 张诗懿, 周亮广,2, 刘凌, 蒋尚明

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.合肥工业大学 水资源与环境系统工程研究所,安徽 合肥 230009; 3.安徽省·水利部淮河水利委员会水利科学研究院 水利水资源安徽省重点实验室,安徽 合肥 230088)

旱灾的影响程度和范围在各种自然灾害中位于前列,严重威胁了我国粮食安全和经济社会发展[1-2]。21世纪以来,随着由传统的消极被动抗旱、应急管理向积极主动抗旱、风险管理转变,旱灾风险管理逐渐兴起,其中旱灾风险评估是旱灾风险管理的核心内容[2-3]。根据自然灾害风险系统理论,区域旱灾风险系统是由危险性、暴露性、灾损敏感性、抗旱能力4个子系统综合作用形成的[4-5]。从以“干旱危险性-旱灾脆弱性-旱灾损失风险”链式传递为基本结构的旱灾风险形成机理可看出,降低干旱危险性或者旱灾脆弱性能有效降低旱灾风险[6]。因此,准确评估区域旱灾风险及其子系统发展趋势、识别主要脆弱性指标并加以诊断对区域旱灾风险防控具有重要意义[7]。目前,区域旱灾风险评估方法主要有信息扩散法[8]、云模型[9]、模糊风险矩阵[10]和集对分析方法[11]等。其中,集对分析方法可从同异反3个方面深入探讨评价样本与等级标准之间的模糊不确定性关系,为区域旱灾风险评估提供了有效途径,因此被广泛应用。然而,在采用集对分析方法进行评估时,现有研究大多未考虑联系数系统结构内各分量间的微观动态运动,造成区域旱灾风险评估结果出现偏差。此外,为了得到完整的联系数值,需要确定联系数表达式中的差异度系数,而由现有的差异度系数确定方法(主要有专家估测法[12]、梯形模糊数法[13]、灰色关联度法[14]、三角模糊数法[15])得到的差异度系数比较粗糙,造成区域旱灾风险评估结果与实际相差较大。针对未考虑联系数分量间的动态演化、差异度系数取值粗糙等问题,本文利用半偏联系数思想构建迁移率矩阵修正联系数分量,并提出一种随样本数据变化而变化的动态差异度系数计算方法,由此构建基于半偏联系数和动态差异度系数的区域旱灾风险评估方法,将其应用于亳州市旱灾风险评估中。

1 基于半偏联系数和动态差异度系数的区域旱灾风险评估方法构建

步骤1在综合分析影响区域旱灾风险的自然条件和社会经济条件的基础上,依照指标体系的构建原则[16],运用遗传层次分析法[17]对评价指标进行筛选并计算各指标的权重,根据区域旱灾风险相关成果[18],构建区域旱灾风险评估指标体系{xj|j=1,2,…,nj}、评价等级标准{skj|k=1,2,…,nk;j=1,2,…,nj}、评价指标样本集{xij|i=1,2,…,ni;j=1,2,…,nj}。其中:xj为区域旱灾风险评估指标体系中的第j个评价指标值;skj为指标j的第k个评价等级标准;xij为第i个样本第j个评价指标值;ni、nj、nk分别为区域旱灾风险评价样本、评价指标、评价等级的数量。本文参照文献[18]将区域旱灾风险划分为4个等级,1级、2级、3级、4级分别对应区域旱灾风险处于微险、轻险、中险、重险时的状态,旱灾风险等级代表区域面临旱灾威胁的程度,风险等级越高,区域面临旱灾威胁的程度越强。

步骤2计算旱灾风险评估样本指标值联系数uijk[19]:

(1)

(2)

(3)

(4)

式中:随评价等级增大而评估样本值增大的指标为正向指标;随评价等级增大而评估样本值减小的指标为反向指标;s1j、s2j、s3j分别为指标j等级1级和2级、2级和3级、3级和4级之间的临界值。

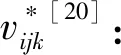
(5)

归一化处理式(5),得相应的旱灾风险评估单指标联系数分量vijk[21]:

(6)

由式(6)算得的联系数分量可构成单指标值联系数uij[22]:

uij=vij1+vij2I1+vij3I2+vij4J。

(7)

式中:I1、I2均为差异度系数;J为对立度系数,J=-1。

步骤3构建迁移率矩阵,计算修正后的单指标联系数分量。现有研究大多将式(6)计算所得的联系数分量直接代入联系数表达式中,将计算所得的联系数值应用于各种实际问题的综合评价中,显然这样的评价结果缺乏稳健性[23]。根据矛盾的普遍性、运动的绝对性原理[20,22-23]和集对分析理论[22]可知,联系数系统结构内的各联系数分量并不是相互独立的,他们之间存在某种转化机制,为了定量刻画这种转化关系,依据半偏联系数思想构建迁移率矩阵X[24]:

(8)

以分量a为例,其余分量以及a本身都会向a迁移转化一定数值,a向自身迁移的可能性为1;∂+a反映了b1向a的迁移率,即b1向a迁移的可能性大小,b1∂+a即为b1向a迁移的数值;∂+b1∂+a反映了b2向a的迁移率,这时a和b2之间的b1承接了这种转化关系,b2∂+b1∂+a为b2向a迁移的数值;∂+b2∂+b1∂+a反映了c向a的迁移率,这时a和c之间的b1、b2承接了这种转化关系,c∂+b2∂+b1∂+a为c向a迁移转化的数值。其余分量迁移转化过程与此相似。

原样本单指标值联系数分量矩阵U=[a,b1,b2,c]经式(8)修正后得到新的联系数分量矩阵R:

(9)

将式(7)中的联系数分量vij1、vij2、vij3、vij4代入式(9)进行修正,再经式(6)归一化,得修正后的单指标值联系数分量v′ij1、v′ij2、v′ij3、v′ij4及联系数u′ij:

u′ij=v′ij1+v′ij2I1+v′ij3I2+v′ij4J。

(10)

式中:I1、I2均为差异度系数,其中I1在[0,1]上取值,I2在[-1,0]上取值;J为对立度系数,J=-1。

步骤4差异度系数I是差异度转化为同一度和对立度的重要纽带。式(8)构建的迁移率矩阵定量刻画了联系数系统结构中各分量间相互迁移转化的动态演化特性,而差异度系数I在此基础上深化表达了这种迁移转化过程。以四元联系数为例,I1、I2的物理意义可解释为将差异度b1、b2转化为同一度a或对立度c的程度,而转化方向、程度大小应和评价样本值与各标准等级间的接近程度密切相关,即I1、I2的值是随样本值的变化而变化的。由参考文献[25]可推知:当评价指标样本值xij越靠近标准等级1级的下限值s0j时,I1ij越接近于1;当xij越靠近标准等级1级和2级的临界值s1j时,I1ij越接近于3/4;当xij越靠近标准等级2级和3级的临界值s2j时,I1ij越接近于1/2;当xij越靠近标准等级3级和4级的临界值s3j时,I1ij越接近于1/4;当xij越靠近标准等级4级的上限值s4j时,I1ij越接近于0。同理,当评价指标样本值xij越靠近标准等级1级的下限值s0j时,I2ij越接近于0;当xij越靠近标准等级1级和2级的临界值s1j时,I2ij越接近于-1/4;当xij越靠近标准等级2级和3级的临界值s2j时,I2ij越接近于-1/2;当xij越靠近标准等级3级和4级的临界值s3j时,I2ij越接近于-3/4;当xij越靠近标准等级4级的上限值s4j时,I2ij越接近于-1。对照文献[25],可推导出I1ij、I2ij的具体计算公式(式(11)和式(12))。

(11)

(12)

式中:s1j、s2j、s3j分别为指标等级1级和2级、2级和3级、3级和4级之间的临界值,s0j、s4j分别为1级的下限值和4级的上限值。

步骤5将式(11)和式(12)计算所得的差异度系数代入式(10),计算评价样本i指标j的四元联系数u″ij[26]:

u″ij=v′ij1+v′ij2I1ij+v′ij3I2ij+v′ij4J。

(13)

由式(13)可得样本i的联系数u″i[26]:

(14)

式中:I1ij、I2ij均为差异度系数;J为对立度系数,J=-1;wj为评价指标j的权重。

依据式(14)计算所得的联系数值判别区域旱灾风险等级值,u″i∈[-1.0,1.0],按照均分原则将其划分为4个等级,分别对应区域旱灾风险状态处于重险u″i∈[-1.0,-0.5)、中险u″i∈[-0.5,0)、轻险u″i∈[0,0.5)、微险u″i∈[0.5,1.0]。

同时,为了和式(14)计算所得的联系数值做比较,计算样本i的半偏减法集对势值[23],并将其划分为4个等级,分别对应区域旱灾风险状态处于重险s∈[-1.0,-0.5)、中险s∈[-0.5,0)、轻险s∈[0,0.5)、微险s∈[0.5,1.0]。

步骤6依据式(13)计算评价指标联系数值u″ij,据此识别对旱灾风险影响较大的指标,并对这些指标进行重点分析。

为进一步验证式(13)的合理性,计算四元半偏减法集对势[19]s(u)和本文方法u″的平均绝对误差d,计算公式为[18]:

(15)

式中M为随机模拟四元联系数的次数。本文分别随机模拟105和106次时,平均绝对误差d为2.5%左右。式(15)利用u″来检验四元半偏减法集对势计算式s(u)的稳定性。通过上述计算可知,s(u)和u″之间的差距较小,也间接验证了利用半偏联系数构建迁移率矩阵修正单指标联系数分量并结合动态差异度系数计算四元联系数值的合理性、稳健性。

2 实例应用

亳州市位于安徽省西北部,由于受全球气候变暖和局部气候的影响,近年来当地干旱灾害频发,严重影响了当地农业发展。因此,准确评估旱灾风险以及识别脆弱性指标对当地农业稳定、健康发展具有重要意义。在对旱灾风险评估的含义和目标综合考虑分析的基础上,依据全面性、层次性、适用性、可操作性原则[16,27],将旱灾风险分为危险性、暴露性、灾损敏感性、抗旱能力4个子系统,4个子系统中指标及其等级标准参照文献[18],各指标权重通过基于加速遗传算法的层次分析法[17]求得,结果见表1[18]。

表1 旱灾风险评估指标、等级标准和权重

根据表1,将2008—2020年亳州市旱灾风险评估指标数据和各指标等级标准代入式(1)—(6),算得各单指标联系数分量,再代入式(9)进行修正,可得修正之后的单指标联系数分量,根据式(11)和式(12)计算各单指标联系数的动态差异度系数,再根据表1中各指标权重和式(14)计算出亳州市旱灾风险评估指标联系数值。同时,为了进一步说明这种联系数值计算方法的稳健性,将计算所得联系数值与半偏减法集对势值进行对比分析,结果见表2。

表2 亳州市旱灾风险及其子系统评估结果值

由表2可知,本文联系数值方法和半偏减法集对势的评估结果基本一致,说明基于半偏联系数和动态差异度系数的联系数值方法的可靠性、稳健性。本文联系数值方法从微观层次深刻挖掘了联系数系统结构中各分量间的迁移运动信息,根据半偏联系数思想构建迁移率矩阵修正联系数分量;同时,本文联系数值方法深刻挖掘了样本中所蕴含的信息,提出随样本值变化的动态差异度系数计算方法。因此,相较于半偏减法集对势,本文联系数值方法的判别敏感度更高、结果更可靠。

为进一步分析2008—2020年亳州市旱灾风险的变化趋势,将表2评估结果绘制成图1。

图1 旱灾风险及其子系统评估结果趋势图

由表2和图1(a)可看出:①2008—2020年亳州市旱灾风险系统中的危险性子系统基本处于轻险、中险两种状态;两种方法计算所得的评估结果值的变化幅度较大,说明危险性子系统内的相关样本指标不稳定且处于不利状态。②两种方法得到的风险状态判别结果基本一致,只有2020年的略微不同,但2020年两种方法计算得到的评价结果值仅相差0.037。比较样本指标数据和评价标准可知,2020年单位面积水资源占有量x1,4和土壤类型x1,6均处于中险状态,而危险性子系统中其余4个样本指标均处于微险或轻险状态,利用联系数值法判别危险性子系统2020年的风险状态为轻险更符合指标数据的实际情况,说明本文联系数值法更具合理性、稳健性。

由表2和图1(b)可看出:2008—2020年亳州市暴露性子系统的风险处于轻险、中险两种状态;两种方法计算所得的评估结果值整体变化幅度较小,只有2013—2014年的变化较大,并且旱灾风险状态从中险向轻险发展,说明在这期间暴露性子系统中的某些样本指标有较大程度的改善。

由表2和图1(c)可看出:①2008—2020年亳州市旱灾风险系统中的灾损敏感性子系统的风险基本处于微险状态,说明灾损敏感性子系统对亳州市旱灾风险降低的影响较大。②两种方法的风险状态判别结果基本一致,只有2008年的略微不同,但2008年两种方法的计算结果仅相差0.047。比较样本指标数据和评价标准可知,2008年农业人口比例x3,1处于中险状态,而灾损敏感性子系统中其余3个样本指标处于微险或轻险状态,利用联系数值法判别灾损敏感性子系统2008年的风险状态为轻险更符合指标数据的实际情况。

由表2和图1(d)可看出:2008—2020年亳州市旱灾风险系统中的抗旱能力子系统风险处于中险状态,说明抗旱能力子系统是造成亳州市旱灾风险状态较高的关键子系统;2008—2020年两种方法得到的评价结果值的整体变化趋势不断上升,说明在这期间亳州市可能进行了相关水利工程建设,使得当地抗旱能力得到增强。

由表2和图1(e)可看出:①2008—2020年亳州市旱灾风险综合系统处于轻险、中险两种状态,并且整体变化趋势从中险向轻险发展;旱灾风险评估结果值变化起伏较小,说明在这期间亳州市旱灾风险有一定程度的降低并且比较稳定。②两种方法的风险状态判别结果在2009年、2010年、2012年和2013年略微不同,但其评价结果值仅相差0.027、0.031、0.044和0.045。以2009年为例,比较样本指标数据和评价标准可知,综合系统中13个样本指标处于重险或中险状态,其余8个指标处于轻险或微险状态,利用联系数值法判别综合系统2009年的风险状态为中险更符合指标数据的实际情况。

为了进一步分析亳州市旱灾风险状况的改善原因,由式(13)计算21个样本指标的联系数值(表2),据此识别并重点分析旱灾风险系统中的脆弱性指标,具体结果如图2所示。

从图2(a)可以看出:在危险性子系统中,降雨负距平百分率x1,1、年均降雨量x1,2两个指标大多数年份均处于微险、轻险状态,说明这两个指标是降低危险性子系统风险的主要指标;相对湿润度指数x1,3仅在2009—2013年、2015年和2019年处于中险状态,说明在这期间亳州市水分含量不足;单位面积水资源占有量x1,4、土壤类型x1,6两个指标常年处于中险、重险状态,说明这两个指标是导致危险性子系统风险较高的主要因子;土壤相对湿度x1,5仅在2010—2014年和2019年处于中险状态,且联系数值接近0,而在其余年份基本处于微险状态,说明其不是导致危险性子系统风险较高的主要指标。

从图2(b)可以看出,在暴露性子系统中,人口密度x2,1基本处于中险状态,耕地率x2,2基本处于重险状态,说明这两个指标是造成暴露性子系统风险状态较高的主要指标;复种指数x2,3在2008—2013年基本处于中险状态,在2014—2020年基本处于微险状态,在2013—2014年从中险状态转为微险状态,说明在2013—2014年亳州市农业发展速度较快;农业GDP占地区生产总值比例x2,4在2008—2020年的联系数值不断上升,说明在这期间亳州市农业经济不断发展。

从图2(c)可以看出:在灾损敏感性子系统中,农业人口比例x3,1在2008—2020年间均处于中险和重险两种状态,说明这个指标是造成灾损敏感性子系统风险状态较高的主要指标;水田面积比x3,2、万元GDP用水量x3,3和森林覆盖率x3,4在2008—2020年基本处于微险状态且变化波动较小,说明这3个指标已经趋于稳定并且能有效降低灾损敏感性子系统的风险水平。

从图2(d)可以看出:在抗旱能力子系统中,单位面积现状供水能力x4,3和单位面积应急浇水能力x4,5这两个指标常年处于中险状态,水库调蓄率x4,2和节水灌溉率x4,7常年处于重险状态,说明这4个指标是造成抗旱能力子系统风险较高的主要指标;人均GDPx4,1常年处于微险状态且联系数值不断上升,说明这个指标可有效降低抗旱能力子系统的旱灾风险;灌溉指数x4,4和监测预警能力x4,6在2008—2020年的联系数值整体呈上升趋势,说明在这期间亳州市基础水利工程建设水平和监测预警能力有所提高。

3 结论

为了定量刻画联系数系统结构内各分量间的微观动态运动,本文基于半偏联系数思想构建了四元联系数的迁移率矩阵,修正单指标联系数分量,并基于样本指标与标准等级间的不确定关系,采用一种随样本指标变化的动态差异度系数计算方法,计算四元联系数的差异度系数I1、I2,构建了基于半偏联系数和动态差异度系数的区域旱灾风险评估方法并应用于亳州市,得到以下结论:

1)本文联系数方法和半偏减法集对势评估结果基本一致,随机模拟得到的平均绝对误差在2.5%左右,验证了利用半偏联系数修正单指标联系数分量,结合动态差异度系数计算四元联系数方法的合理性。

2)2008—2020年,危险性子系统的风险状态基本处于轻险和中险两种状态,并且评估结果值的变化幅度较大,其中单位面积水资源占有量和土壤类型是脆弱性指标;暴露性子系统的风险状态处于轻险和中险两种状态,并且评估结果值的变化幅度较小,其中人口密度和耕地率是脆弱性指标;灾损敏感性子系统的风险状态基本处于微险状态,其中农业人口比例是脆弱性指标;抗旱能力子系统的风险状态处于中险,其评估结果值整体呈上升变化趋势,其中水库调蓄率、单位面积现状供水能力、单位面积应急浇水能力和节水灌溉率是脆弱性指标;综合系统的风险状态处于轻险和中险状态,并且整体变化趋势从中险向轻险发展。

3)在今后的研究中,要进一步深入挖掘联系数系统结构中各分量间的动态演化关系,探索评价样本指标与评价标准等级之间的不确定关系,并采用动态差异度系数加以量化,以期为解决各种不确定性问题提供有效途径。