Churning loss characteristics of a wet three-phase high-speed reluctance motor
Zhenzhou ZHANG, Mingzhu DAI, Chenchen ZHANG, Yi CHEN, Bin MENG
Research Article
Churning loss characteristics of a wet three-phase high-speed reluctance motor

College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310023, China
With the increasing requirements of electro-hydrostatic actuators (EHAs) for power, volume, and pressure, there is a growing tendency in the industry to combine the motor and pump to form a so-called ‘motor pump’ to improve the integration. In this paper, a novel structure for a wet three-phase high-speed reluctance motor pump is proposed, which can further improve integration by removing the dynamic seal on the pump shaft, thereby avoiding the problems of dynamic seal wear and oil leakage and improving heat dissipation under high-speed working conditions. However, after the motor is wetted, the churning loss caused by immersion of the rotor in the oil causes additional fluid resistance torque. Based on fundamental fluid mechanics, an analytical model of the churning torque of a wet motor was established. To verify the accuracy of the analytical model, a simulation model of churning loss was established based on computational fluid dynamics (CFD), and the churning torque and flow field state were analyzed. Finally, an experimental prototype was designed and manufactured, and a test bench for churning loss was built. The oil churning torque was measured at different speeds and temperatures. The results from the analytical, simulation, and experimental models agreed well. The experimental results validated the analytical model and CFD simulation. This research provides a practical method for calculating the churning loss and serves as guidance for future optimization of churning loss reduction.
Motor pump; Wet motor; Churning loss; Analytical model; Computational fluid dynamics (CFD)
1 Introduction
Electro-hydrostatic actuators (EHAs) are highly integrated hydraulic systems composed of motors, hydraulic pumps, tanks, cylinders, test elements, and other components (Ge et al, 2021). As early as the 1960s, American aviation scholars proposed that EHAs have outstanding advantages in integration and power-to-weight ratio (Wang et al., 2020; Ge et al., 2021; Lei et al., 2021), which help to meet the requirements of military aircraft for high speed, high mobility, and high energy efficiency. They overcome the shortcomings of traditional centralized hydraulic systems and thus play a key role in the performance of such systems (Jensen et al, 2021). EHA technology has not been limited to the aerospace field (Chao et al., 2019; Jiao et al., 2022), but has been widely used in mechanical engineering, intelligent robotics, and other fields (Song et al., 2019; Kittisares et al., 2022; Zhu et al., 2022).
As a crucial part of an EHA, the hydraulic pump greatly influences its performance. Recently, to improve the integration of EHAs and to broaden their application field, the industry proposed a so-called 'motor pump' with a high degree of integration of the motor and hydraulic pump (Zhu BH et al., 2018), which has obvious advantages over its traditional counterparts.
Earlier motor pumps used a 'three-section' structure, i.e., motor, coupling, and pump (Cai, 2018). Since the moving components of the pump are immersed in oil, a rotating dynamic seal is required on the coupling between the motor and the pump to isolate the pump cavity from the rotor cavity of the motor. The seal prevents pressurized oil from entering the motor, which could potentially damage the excitation coil. However, such a rotating dynamic seal is liable to fail under high-speed conditions, resulting in oil leakage in the pump casing, seriously affecting the reliability of the motor pump operation. Therefore, an electric motor with a wet structure was developed (Jin et al., 2021). The wet motor allows oil to enter the rotor cavity through a special oil pressure-resistant design. This eliminates the need for the rotating dynamic seal on the pump shaft and thus has better reliability than a dry motor. Therefore, the structure of wet motors has been the focus of recent research in the industry.
Claar and Hodges (1998) developed an integrated motor pump (IMP) by connecting the motor and hydraulic pump axially, thereby reducing leakage and noise. The oil wets the stator and rotor of the motor, removing the heat generated inside the motor and enhancing heat dissipation. SAUER BIBUS (1999) designed a variable motor pump combining an asynchronous motor and a variable axial piston pump. The piston pump cylinder is assembled directly inside the motor rotor, thus reducing the axial size of the motor pump and further improving the integration of the motor pump. This also eliminated the need for a dynamic seal on the shaft to realize a motor pump without external leakage, and reduced noise and pressure pulsation. Ji et al. (2010, 2014) integrated a vane pump with an asynchronous motor and investigated the electromagnetic field, temperature field, flow field, and other aspects of the motor pump. Compared with the conventional structure, the axial size of this motor pump was reduced by about 61% and the volume by about 50%. Zhang et al. (2008) and Gao et al. (2010) conducted extensive research on axial piston hydraulic motor pumps. They simulated the internal flow field and the electromagnetic field of the motor pump to provide a reference for the design of the motor pump. Fu et al. (2017) integrated an axial piston pump with a three-phase asynchronous motor to form a so-called 'motor pump'. The efficiency and loss issues were analyzed and verified via simulation.
Based on research on the oil-immersed structure of motor pumps, the use of enameled wires is a simple and convenient method to isolate the impact of oil on the coil. However, in most cases where the motor pump is immersed in oil, the use of enameled wires alone can lead to severe leakage hazards and poor safety when wear occurs. Furthermore, because the motor pump in this study was designed for use in high-speed hydraulic aviation pumps at a speed of approximately 10000 r/min, the flow field is more agitated. Thus, the friction between the oil and the enameled wire is intensified, increasing the likelihood of damage to the enameled wire. To overcome this problem, we propose a high-pressure-resistant structure for a wet three-phase high-speed reluctance motor pump, which uses the static sealing structure of an O-ring to isolate the coil from the oil. Compared with previous structures, the new structure is simple, reliable, and easy to implement.
After a motor is wetted, the original air gap of the motor is filled with oil to form a so-called 'oil gap'. This leads to churning loss caused by the oil (Li et al., 2020), resulting in a reduction of the whole motor efficiency. Therefore, it is necessary to investigate the churning loss to provide a basis for subsequent structure optimization to reduce its effects. Oil churning loss has often been analyzed in studies of high-speed axial aviation piston pumps. Zhang (2022) studied an oil-immersed axial piston motor pump and established analytical models for oil friction loss, leakage loss, electromagnetic heat generation loss, and mechanical friction loss. An analytical model of the churning loss of an oil-immersed motor was established by converting the wind friction loss equation into the oil-liquid friction loss equation and simplifying the stator and rotor as cylinders. Li et al. (2014) analyzed various mechanical losses of axial piston electro-hydraulic pumps, established a model for calculating mechanical efficiency, and presented the curves of oil gap losses between the stator and rotor with respect to speed, pressure, and temperature. Wang et al. (2022) designed an oil-filled motor that can be used at full-ocean depths and investigated the friction losses caused by the rotation and properties of the oil. When the motor is wetted, the outer wall of the rotor and the inner wall of the stator form inner and outer walls, respectively, which are similar to annular oil gaps. The presence of tooth grooves on the wall makes the fluid flow in an annular air gap extremely complex, and the Taylor-Couette flow ultimately occurs (Taylor, 1923). Lee and Minkowycz (1989) studied the flow in an annular air gap when the cylinder was grooved axially. The results indicated that the pressure drop in the Taylor-Couette flow generated by the axial groove design was greater than that in the smooth flow between the inner and outer cylinders. This results in an increase in the differential pressure resistance torque during operation, i.e., an increase in the churning loss. Borujerdi and Nakhchi (2017) investigated the effect of different tooth slot aspect ratios and the number of tooth slots on the heat transfer and pressure drop ratio between air gaps using a response surface method. In summary, rather than considering industrial low-speed motors, in this study, we focused on the problem of excessive oil churning torque during the operation of integrated high-speed wet motors for aviation. The churning losses were studied with a focus on flow fields with a tooth-slot structure between the stator and rotor walls of the wet motors.
With the increasing requirements of EHAs for power, volume, and pressure, there is a growing tendency in the industry to combine the motor and pump to form a motor pump to improve the integration. In this paper, a novel structure for a wet three-phase high-speed reluctance motor pump is proposed. The design improves integration by removing the dynamic seal on the pump shaft while avoiding the problems of dynamic seal wear and oil leakage, and improves heat dissipation under high-speed working conditions. However, once the motor is wetted, the churning loss caused by immersion of the rotor into the oil causes additional fluid resistance torque, which needs to be analyzed in detail.
The rest of this paper is organized as follows: In Section 2, the structure and working principle of the wet three-phase high-speed reluctance motor pump are described. In Section 3, an analytical model of the oil churning torque is established. In Section 4, a computational fluid dynamics (CFD) simulation of churning loss is described, including the establishment of a wet motor flow domain model and a set of simulation parameters. In Section 5, the CFD simulation results of churning loss are analyzed, including the flow field and oil churning torque changes under different conditions. In Section 6, a wet motor oil churning test bench is established, and experimental research on the prototype is described. Finally, conclusions from this work are drawn in Section 7.

Fig. 1 Schematic diagram of the structure of the wet three-phase high-speed reluctance motor pump
2 Structure and working principle
The structure of the wet three-phase high-speed reluctance motor pump is shown in Fig. 1. It consists mainly of a wet three-phase high-speed reluctance motor (denoted as the wet motor) and a stacked roller 2D piston pump (Jin et al., 2019; Zhang et al., 2021). Note that the proposed wet motor can form a motor pump with any hydraulic pump, not only a stacked roller 2D piston pump. The wet motor consists mainly of a stator made of four sections of yoke iron, three sections of the rotor, control coils, coil holders, and front and rear end caps. Fifteen rectangular teeth are evenly distributed on the inner circular surface of the stator made up of the four yoke iron sections, and the coil holders are placed between yokes A and B, B and C, and C and D, where the control coils are wound to form a three-phase current control. The 15 rectangular teeth are also evenly distributed on the outer circular surface of the three rotor sections, and the three rotor sections are misaligned with each other by 1/3 tooth pitch angle, so that six working air gaps are formed between the rotor and the stator from left to right (δ1, δ2, δ3, δ4, δ5, and δ6).
In a traditional dry motor, when connected to the pump shaft, a rotating dynamic seal needs to be added to isolate the pump cavity from the rotor cavity of the motor to prevent pressurized oil from entering the motor, potentially damaging the excitation coil. However, such a rotating dynamic seal is liable to fail under high-speed conditions, resulting in oil leakage in the pump casing, which seriously affects the reliability of the motor pump operation. As our proposed motor adopts a wet concept design, the dynamic seal at the pump shaft can be omitted, which greatly improves the reliability of the whole motor pump. Fig. 1 shows that when oil enters the motor rotor chamber, there is an annular groove on the inner side of the front and rear covers for the O-ring to prevent the oil from leaking out of the mating gap between the parts. The inner holes of the three coil holders are machined with a pair of annular grooves arranged evenly on the left and right to position the O-rings so that the control coils can be isolated from the rotor chambers filled with oil. The circulating flow of oil can also take away the heat generated by the coil, thereby improving the heat dissipation of the motor. This wet structure is simple, reliable, and easy to realize. However, the churning loss caused by immersion of the rotor into the oil will cause additional fluid resistance torque, so it is necessary to study the churning loss.
The working principle of the proposed wet motor is shown in Fig. 2. The magnetic field always moves along the path with the least reluctance. When none of the three-phase control coils are energized, none of the working air gaps (δ1, δ2, δ3, δ4, δ5, and δ6) form between the stator and the rotor work. When one of the phase control coils is excited (Fig. 2), the control magnetic field generates a tangential magnetic force, causing the rotor to rotate. Because the teeth of the stator and rotor are misaligned, their relative positions and the magnetic conductivity of the magnetic circuit are different. Rotation of the rotor ensures the minimum reluctance of the magnetic circuit. Continuous rotation of the motor can be realized by changing the sequence of energization between the three-phase coils.

Fig. 2 Magnetic circuit diagram of one-phase coil excitation
3 Analytical modeling
When the wet motor is running, the stator is fixed, and the rotor rotates at a constant speed, where the oil gap is between the stator and the rotor. The fluid flow pattern within the oil gap is defined by the Taylor number. The formula for the Taylor number () and the corresponding critical Taylor number (c) can be written as (Zhu YC et al., 2018):


whereis the angular velocity,is the radius of the rotor,his the hydraulic diameter, andis the kinematic viscosity.
Because the rotating speed of the wet motor is generally high, the actual Taylor number of the internal fluid flow is far greater than the critical Taylor number, so the internal flow field of the wet motor is mainly a turbulent Taylor vortex.
The stator and rotor of the motor have a toothed structure. Influenced by the rotation of its wall surface, the oil churning loss of the motor comes mainly from three different sources. The first is the resistance torque coming from the shear friction resistance between the stator and rotor. The second is the resistance torque coming from the fluid flow resistance force during oil churning on the side of the rotor. The third is the resistance torque coming from the shear friction resistance when the end face of the rotor rotates. These three parts of churning torque during motor operation were analyzed using the following analytical model.
3.1 Churning torque of the rotor circumference
Fig. 3 shows a sectional diagram of the stator and rotor. Where the circumferential surface of the rotor tooth shape is marked with dashed lines, it can be regarded as the flow between coaxial rotating cylinders (Zou et al., 2013).

Fig. 3 Sectional diagram of the stator and rotor. r1is the radius of the rotor tooth root circle; r4is the radius of the stator tooth root circle
The velocity distribution in different directions between cylinders is defined as follows:Vis the radial partial velocity,Vis the circumferential partial velocity, andVis the axial partial velocity. In the equilibrium state, we assumed that the flow field is steady and axisymmetric, and the fluid flow is limited to the plane of rotation, which does not move along the axis of rotation. Taking the flow between two cylinders with radii2and3as an example, the velocity () distribution between the two cylinders can be expressed as:

where2is the radius of the rotor addendum circle,3is the radius of the stator addendum circle,1is the rotation speed of the inner cylinder, and2is the rotation speed of the outer cylinder.
The motor drives the rotor to churn oil during real operation. At this time, the outer cylinder wall is stationary (2=0). When the inner cylinder rotates and the outer cylinder is stationary:

where=2/3is the ratio of the two radii of the cylinder,=/2is the relative radius of flow, and1=12is the circumferential velocity of the inner circle.
The distribution of tangential stress perpendicular to theanddirections (τ) in the flow field is:

whereis the oil viscosity, andSis the area of the fluid perpendicular to the direction.
SubstitutingV=(),V=0, and Eq. (4) into Eq. (5) yields:

The negative sign in Eq. (5) indicates the tangential stress of the inner fluid acting on the outer fluid (Fig. 3 counterclockwise). The tangential stresses acting on the inner and outer cylinder surfaces by the viscous fluid are expressed respectively as follows.
On the outer surface of the inner cylinder=2,

On the inner surface of the outer cylinder=3,

When the radius is(2<3), the outer cylindrical surface is stationary, and the inner cylindrical surface is rotating, the rotational resistance torque () of the inner cylindrical surface subjected to the fluid per unit height can be expressed as:

Based on the above equation for the flow between the walls of the two cylinders and the actual radius of the circular surface, the formula for the resistance torque between the four different radii of the toothed rotor and stator can be obtained in the same way.
Since the circumference surfaces of the stator and rotor are toothed, there are two gaps1(3-1) and2(4-1) between the concave surface of the rotor tooth and the stator in the process of rotation. The convex surface of the rotor tooth has two gaps3(3-2) and4(4-2) relative to the stator during rotation. After calculation, the proportion of the arc length of the tooth surface corresponding to each radius to the complete circle is about:




Substituting Eqs. (10)–(13) into Eq. (9) to obtain the churning torque of the rotor circumference surface (R) gives:

However, the internal flow field of the motor is complex during operation. The above calculation applies only to laminar flow. Therefore, the calculation needs to add a correction coefficientRfor the circumferential shearing flow (Huang et al., 2020). The final circumferential shear torque on a single rotor section can be expressed as:

The fluid resistance torque acting on the total length of three rotors (the length of a single rotor is) is calculated as follows:

3.2 Churning torque of the rotor side
As shown in Fig. 4, when the rotor moves in the viscous fluid at a rotational speed of1, its side will be subjected to the corresponding fluid force (D) consistent with the direction of the incoming flow. SinceDis opposite to the moving direction of the rotor, it is a resistance force. Therefore, for high-speed rotating rotors, the formula for calculating the fluid flow resistance can be obtained as (Li et al., 2016):

Fig. 4 Schematic diagram of the rotor side. h is the tooth height

whereDis the friction resistance coefficient,is the fluid density,is the tangential speed of rotor movement, andDis the projected area of the object perpendicular to the flow direction.
From Eq. (17), the friction resistance acting on the unit area is:


whereDis the churning torque of the rotor side.
3.3 Churning torque of the rotor end face
The three rotors have a total of six end faces, and the end faces are the same (Fig. 1). The oil churning loss of the overall end face can be obtained by fixing one of them. The rotor end face is shown in Fig. 5.
According to the non-slip condition of the wall surface of the fluid resistance, the fluid adhering to the rotor surface makes the rotor subject to viscous shear stress during the rotation process, i.e., the frictional resistance of the fluid to the object. The friction resistance of the rotor during rotation is related to the fluid–solid contact area, the roughness of the rotor, the viscosity of the liquid, and other factors.

Fig. 5 Schematic diagram of the rotor end face. dθ is the unit angle, dS1is the unit area in circular area, and dS2is the unit area in rectangular area
When calculating the area integration of the above end faces, it is necessary to divide the calculation of the resistance torque of the end faces into the circular part within the dashed line and the 15 rectangular tooth parts outside the dashed line (Fig. 5), using the polar coordinate system and the rectangular coordinate system, respectively.
The formula for the resistance torque of the end face rotation on any element area on the circumference of the end face can be written as (Zhang, 2020):

whereis the shear stress of fluid,is the microelement area on the end face,is the unit length in tooth width direction,is the rotor tooth width, andis the distance between rotor end faces.
Substituting the end face parameters yields the churning torque of the rotor's circumferential end faceE1:

where0is the radius of the rotor shaft.
The rotation resistance torque of the end face on any micro-element area on a single-toothed end face can be written as:

Substituting the end face parameters yields the churning torque of the rotor's rectangular end faceE2:

Therefore, the total end face resistance torque of the rotor (E) can be written as:

Due to the instability of the fluid at high rotational speeds, the correction coefficientEof the end face shearing flow (Huang et al., 2020) is added here, giving:

3.4 Total oil churning torque
From the above solution to the churning loss of the rotor's circumference, side, and end face during movement, the total churning torque (t) can be written as:

4 CFD simulation and discussion
4.1 Fluid domain model and parameters
As shown in Fig. 6, according to the tooth size of the stator and rotor of the proposed wet motor, the fluid domain model required for the CFD simulation was established and appropriately simplified (Fig. 6). The size information of the fluid domain model is shown in Table 1.

Fig. 6 Fluid domain model of wet motor: (a) 3D; (b) 2D

Table 1 Fluid domain parameters of wet motor
According to the analysis of the analytical model, the churning torque is directly related to the viscosity of the oil. The viscosity is caused by the intermolecular interaction force. The temperature has the greatest impact on this force. As the temperature increases, the molecular spacing increases, and the viscosity decreases. To verify the effect of temperature on the churning torque, the viscosity–temperature characteristics of oil should be considered. The relationship between the temperature and viscosity of the oil is shown in Table 2 (Liu, 2021).

Table 2 Relationship between temperature and viscosity (46# hydraulic oil) (Liu, 2021)
Based on the corresponding viscosity–temperature characteristic parameters in Table 2, the Reynolds equation was used (Wu et al., 2022) to perform the function fitting of the viscosity–temperature curve. Though the Reynolds equation is simple in form and easy to calculate, its accuracy was not satisfactory, and it is generally used within the temperature range of 20–80 ℃. To make the viscosity–temperature curve more accurate, the Reynolds equation was modified into two forms:

whereoilis the oil temperature (℃), and1,2,3, and4are constants.
Based on the curve fitting of the above Reynolds correction equation, the viscosity–temperature characteristic function of 46# hydraulic oil is obtained as follows:

The function curve is shown in Fig. 7.

Fig. 7 Viscosity–temperature characteristic curve
4.2 Simulation conditions
In CFD simulations, different fluid domain motion pairs should be solved with different models. Considering the high speed of the proposed wet motor, its energy loss occurs mainly near the wall. The-shear stress transfer (SST) model considers the transmission of shear stress, introduces mixed functions to achieve the conversion of the turbulence model in different turbulence scale regions, and has excellent performance for the near wall situation. In this study, by comparing the convergence of different turbulence models, it was reasonable to use the-SST model to simulate the internal fluid domain of the wet motor.
Dynamic mesh and sliding mesh can both be used to simulate and analyze the actual movement of the fluid field inside the wet motor. The dynamic mesh can automatically update the mesh as the flow field boundary changes. The sliding mesh can realize the mutual motion between the flow field regions by applying conditions to the whole mesh region and realize the flow between the two regions through the interface. Through the comparison of simulation results between dynamic mesh and sliding mesh, we found that the oil gap of the fluid domain model of the wet motor is very small (0.3 mm). Although the dynamic mesh can describe the actual working conditions more clearly, it demands a large amount of calculation resource, and the requirements for mesh quality are high. Also, problems such as mesh negative volume may easily occur. In comparison, the sliding mesh is easy to set up, and the calculation time is rapid. The simulation results are close to those from the dynamic mesh where the calculation error is small. Therefore, in this study the sliding mesh method was used to divide the overall fluid domain into the internal moving fluid domain and external stationary fluid domain, as shown in the 3D model in Fig. 6a. The sliding mesh motion was set in the fluid domain near the rotor and the corresponding rotation speed is given. The velocity of the fluid domain near the stator was set to 0. The interface of the two parts of the sliding mesh in the fluid domain was set as 'matching' to realize the data exchange between the fluid domains, and the outer wall of the inner fluid domain and the inner wall of the outer fluid domain were divided further to obtain more accurate simulation results.
All walls in the model were set as non-slip walls. The SIMPLE (semi-implicit method for pressure linked equation) algorithm was used to solve the pressure–velocity coupling problem. The pressure interpolation was set to the second order. The time step was set as the time taken by the actual rotation of the motor for 1°, which was convenient for the analysis of the subsequent simulation results.
4.3 Mesh independence
The mesh is the link between the physical model and the numerical algorithm. The quality of the grid has a great impact on the accuracy of the calculation results, which is related to the speed of iteration convergence and the stability of iteration. With the refinement of the mesh (the mesh cells become smaller and the total number of cells increases), the theoretical simulation error should gradually approach 0, but the actual grid needs only to be densified within the permitted range of the error.
In the operation of designing mesh division, when hexahedral structure mesh is used for a tooth-like complex fluid domain structure, its quality is generally low and errors are often reported. Therefore, a tetrahedral unstructured mesh was used for the fluid domain. The mesh was densified and remaining settings were unchanged. The mesh independence was verified by the CFD simulation result of churning torque. Because the oil gap in the fluid domain was so small, the simulation can run normally only if the mesh quality is improved to be more than 0.8. Therefore, the simulation results with mesh numbers of 1.93 million, 2.53 million, and 3.14 million (grid quality is about 0.80, 0.81, and 0.82, respectively) were compared here.
According to the simulation results of different mesh numbers at an oil temperature of 40 ℃ and a rotational speed of 6000 r/min in Fig. 8, we found that there was a small difference between the simulation results of 1.93 million and 2.53 million meshes. However, the simulation results of 2.53 million and 3.14 million meshes were basically consistent, and tended to be more stable than those of 1.93 million meshes. This shows that the change in the number of meshes affects the result of churning torque: the larger the number of meshes, the more precise the division, and the smaller the effect. Therefore, it is necessary to reduce the number of meshes in the fluid domain as much as possible while still ensuring that the number of meshes has little influence on the churning torque. Finally, 2.53 million fluid domain meshes were selected in this study to perform CFD numerical simulation.

Fig. 8 Mesh independence test
5 Simulation results and discussion
Fig. 9 shows the velocity vector distribution of the flow field section of the wet motor simulated under different speeds when the oil temperature is 40 ℃. Fig. 9 shows that the effect of the tooth slot changes the flow field and produces Taylor vortices. The circumferential velocity in the section annular gap dominates, and the velocity gradually decreases along the radial direction. The velocity in the tooth slot area is relatively small. Fig. 9 shows the velocity distribution in the tooth slot with local amplification, where an obvious Taylor vortex can be observed. With the increase of rotor speed, the flow velocity of the internal vortex gradually increases, which increases the complexity of the whole flow area.

Fig. 9 Velocity vector distribution of the flow field section of the wet motor simulated under different speeds: (a) 3000 r/min; (b) 6000 r/min; (c) 9000 r/min; (d) 12000 r/min
Fig. 10 shows a pressure distribution nephogram of the flow field section of the wet motor simulated under different speeds when the oil temperature is 40 ℃. The pressure gradually increases from the rotor wall to the stator wall, i.e., the pressure at the rotor side is lower than that at the stator side. This is because the fluid velocity near the rotor wall is greater than that near the stator wall. In addition, there are periodic high-pressure and low-pressure zones near the rotor and stator walls. This is because under the combined action of viscous force and centrifugal force, the fluid will generate periodic Taylor vortices in the gap, and under the combined action of the stator wall and the rotor wall, the fluid will generate a relatively obvious velocity gradient near the stator and rotor walls, resulting in periodic pressure variation.

Fig. 10 Pressure distribution nephogram of the flow field section of the wet motor simulated under different speeds: (a) 3000 r/min; (b) 6000 r/min; (c) 9000 r/min; (d) 12000 r/min

Fig. 11 Curve of churning torque of each part
The curve of the churning torque at an oil temperature of 40 ℃ and a speed of 6000 r/min is shown in Fig. 11. Initially, the oil churning process of the motor has not reached a stable state. The total churning torque is still rising, and the increase is large, especially of the side churning torque. As time goes by, the churning torque on the circumference and the end face gradually reaches a steady state, while the side churning torque fluctuates periodically with time and eventually tends to be stable.
When the motor is stabilized, the total churning torque is about 0.212 N·m. The circumferential churning torque is about 0.059 N·m, accounting for 27.83% of the total torque, the side churning torque is about 0.131 N·m, accounting for 61.79% of the total torque, and the end face churning torque is about 0.022 N·m, accounting for 10.38% of the total torque. The side churning torque accounts for more than half of the total churning torque. Therefore, to reduce the whole churning torque, the optimization for the wet motor structure parameters should focus on how to reduce the side churning torque.
Based on the CFD simulation, the variation curves of the churning torque of the circumference, side, end face, and the total can be obtained (Fig. 12). With the increase of rotating speed, the churning torque of all parts increases. The side churning torque increases sharply with the increase of speed. In contrast, the increasing trend of the churning torque on the circumference and end face is relatively flat. When the motor speed is lower than 3000 r/min, the magnitude of the side churning torque is similar to that of the circumferential churning torque, which indicates that the influence of the viscous force on flow is not much different from that of the inertial force on the fluid. When the motor speed is higher than 3000 r/min, the side churning torque is significantly greater than the circumferential counterpart. This indicates that the influence of the inertia force on the flow is more obvious than that of the viscous force, and the greater the speed, the more obvious the difference between the two. We conclude that when working at high speed, how to reduce the side churning torque is the key issue for wet motor design.

Fig. 12 Churning torque of each part at different rotation speeds with an oil temperature of 40 ℃
When the oil temperature is 40 ℃, the analytical values of the churning torque at different speeds were compared with the simulation values (Fig. 13). The correction coefficientsR=0.490,D=0.915, andE=4.217 were used here and in the subsequent analytical value calculation. The rising trends of the analytical value and the simulation value are basically the same. With the increase of motor speed, the churning torque presents a monotonic increasing trend and the gradient of the increase gradually increases. Meanwhile, the difference between the simulation value and the analytical value also increases. When the maximum speed is set to 12000 r/min, the difference between the two is the largest, where the analytical value is about 0.670 N·m, the simulation value is about 0.705 N·m, and the error is about 5.22%. The possible reason is that the correction coefficients in the analytical model are obtained by fitting each sampling point of the CFD simulation results, and the number of sampling points limits the accuracy of the correction coefficients, resulting in the error between the analytical and simulation values.

Fig. 13 Total churning torque at different rotation speeds with an oil temperature of 40 ℃
When the motor speed is fixed at 6000 r/min, the analytical values of the churning torque under different oil temperatures were compared with the simulation values (Fig. 14). In the range of oil temperature from 20 to 70 ℃, the churning torque decreases monotonically with the increase of oil temperature, and the gradient of the decrease gradually decreases. The trend of this curve is similar to that of the viscosity–temperature characteristic curve of oil. Fig. 14 shows that when the oil temperature is between 20 and 40 ℃, the difference between the two curves gradually decreases with the increase of oil temperature. When the oil temperature is between 40 and 70 ℃, the difference between the two curves gradually increases with the increase of oil temperature. That is, the difference between the analytical value and the simulation value at 20 ℃ reaches the extremum when the analytical value is about 0.357 N·m, the simulation value is about 0.392 N·m, and the error is about 9.80%. At an oil temperature of 40 ℃, the analytical value is about 0.217 N·m, the simulation value is about 0.218 N·m, and the error is about 0.46%. At 70 ℃, the analytical value is about 0.165 N·m, the simulation value is about 0.149 N·m, and the error is about 9.70%. The error at the maximum value is less than 10%, but it is obviously larger than that in Fig. 13. The possible reason is that the physical property parameters of the oil are defined based on the case of an oil temperature of 40 ℃ in this study. Although the viscosity of the oil with the main influence factors has been fully considered by the viscosity–temperature characteristic function (Eq. (28)), the oil density and other parameters under different oil temperatures are all simply taken as the values at 40 ℃ and do not change with the oil temperature. Therefore, when the oil temperature is 40 ℃ in Fig. 13, the error between the analytical value and the simulation value is only 0.46%, and as the oil temperature gradually deviates from 40 ℃, the error between the two will gradually increase.
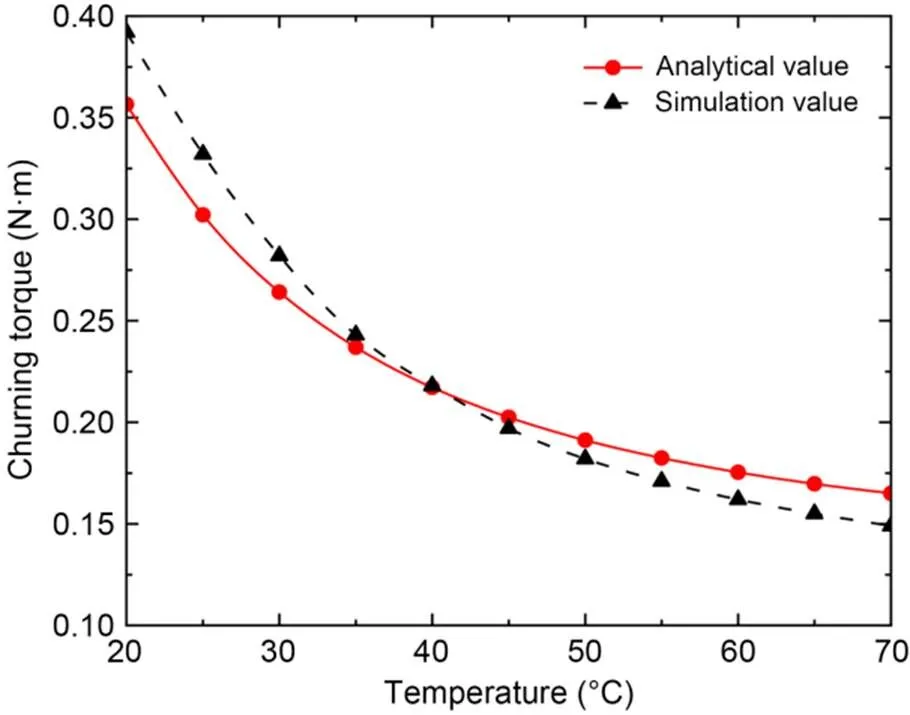
Fig. 14 Churning torque at different oil temperatures with a motor speed of 6000 r/min

Fig. 15 Churning prototype: (a) parts; (b) assembly
6 Experimental validation
To verify the above analytical and simulation results, a churning experimental prototype of the toothed stator and rotor was designed and machined based on the 3D model of the wet motor (Fig. 15). To clearly see the flow field inside the prototype, the stator, rotor, and shaft were made of aluminum, and the front and rear end covers were made of transparent plexiglass material.
Fig. 16 shows the oil churning test bench of the prototype, including the oil churning prototype, electric motor, speed regulator, temperature/torque sensor, temperature/torque acquisition card, 12 V voltage source, signal converter, and personal computer (PC). The oil churning prototype was fixed on the base of the test bench, and the rotor shaft was connected to the torque sensor through the coupling. After powering on, the electric motor was used to drive the prototype, and the speed regulator was used to control and vary the speed of rotation. To obtain the churning torque at different speeds and temperatures, the torque/temperature sensor and the acquisition card were used to monitor the numerical changes in real time at the PC.
To observe the influence of experimental temperature on the churning torque, a temperature sensor on the front end cover and three temperature sensors on the side of the stator were used to measure the temperature of the oil (Fig. 15). The rate of the rise in oil temperature of four temperature sensors at 6000 r/min was measured (Fig. 17). T1 represents the temperature sensor on the front end cover, while T2, T3, and T4 represent the temperature sensors on each of the three sides of the stator on the experimental platform from left to right in Fig. 15, respectively. The temperature of the end face was significantly lower than that of the side. This is because the wet motor has only circumferential rotation movement, and there is no axial movement. Therefore, the heat transfer of the fluid in the axial direction is significantly lower than that in the circumferential direction. Thus, subsequent oil temperature measurement results were based mainly on the average value of the readings of the three temperature sensors on the side of the stator.

Fig. 16 Oil churning test bench of the prototype

Fig. 17 Rate of temperature rise of four temperature sensors at 6000 r/min
The rate of the rise in oil temperature at different speeds was obtained (Fig. 18). With the increase of the motor speed, the rate of the rise in temperature increased gradually, and the gap in the rate of temperature rise between adjacent speeds decreased gradually. However, at the same rotational speed, with the rise of temperature, the rate of the rise in oil temperature decreased. This was caused by the viscosity–temperature characteristics of the oil.

Fig. 18 Rise in oil temperature in the prototype at different rotation speeds
The analytical, simulation, and experimental values of the churning torque at different speeds were compared when the oil temperature was 40 ℃ (Fig. 19). The three churning torque curves presented a monotonic increasing trend with increasing motor speed, and the gradient of the increase gradually increased. Meanwhile, there was a small difference between the analytical, simulation, and experimental values. The difference between the three was the largest when the maximum speed was set to 12000 r/min: the analytical value was about 0.705 N·m, the simulation value about 0.670 N·m, and the experimental value about 0.690 N·m.

Fig. 19 Comparison of churning torque at different rotation speeds at 40 ℃
The analytical, simulation, and experimental values of the churning torque under different oil temperatures were compared when the motor speed was fixed at 6000 r/min (Fig. 20). Because the oil temperature was restricted owing to the use of plexiglass material in the prototype, the temperature range measured in this experiment was 25–40 ℃. In this range, the three churning torque curves showed a monotonic decreasing trend with increasing oil temperature and the gradient of the decrease gradually decreased. Meanwhile, the overall error between the three values gradually decreased with increasing oil temperature, showing two extrema: when the oil temperature was 25 ℃, the analytical value was about 0.302 N·m, the simulation value about 0.334 N·m, and the experimental value about 0.320 N·m; when the oil temperature was 40 ℃, the analytical value was about 0.217 N·m, the simulation value about 0.220 N·m, and the experimental value about 0.210 N·m. The reason for this phenomenon may be related to the viscosity–temperature characteristics of the oil. When the temperature is low, the viscosity has a greater effect on the churning torque, and the numerical error of the three results is large. In contrast, when the temperature is high, the viscosity has a smaller effect on the oil churning torque, and the numerical error of the three results is small.

Fig. 20 Comparison of churning torque at different temperatures at 6000 r/min
Finally, the errors between the experimental results and the simulation and analytical results were also related to the following two aspects: firstly, the existence of bearing and seal loss in the experiment brings errors to the experimental value; secondly, due to the limitation of computer calculation capacity, the numerical simulation in this study was carried out with oil being regarded only as single-phase, which ignores the effect on the wet motor rotor of the gas dissolved in the oil. This would also contribute to the error between the simulation value and the experimental value of the churning torque.
7 Conclusions
1. A novel structure of a wet three-phase high-speed reluctance motor pump is proposed, which eliminates the need of a dry motor structure for a dynamic seal at the pump shaft by using a so-called 'wet motor'. This also simplifies the structure and improves the motor integration level and heat dissipation by the circulating flow of oil. The proposed wet motor structure is simple and easy to realize, which improves the working reliability of the motor pump while avoiding leakage.
2. Based on the theory of fluid mechanics, an analytical model of churning torque was deduced, and a fluid domain simulation model of oil churning based on CFD was established. Through the comparison of different fluid simulation models, motion modes, meshes, and other parameters, the sliding mesh motion mode under the-SST model was finally selected to study the flow field and churning torque. The analytical modeling results were generally consistent with the simulation results, indicating that CFD simulation can provide a good technical reference for the research of wet motor oil churning.
3. An experimental bench was built to study the oil churning of the wet motor. The accuracy of the analytical and simulation results was verified by measuring the churning torque at different temperatures and speeds. The trends of the three curves were basically the same, indicating that the method can provide a reference for further study of structure design and churning loss reduction optimization of wet motors.
4. The side churning torque of the wet motor accounted for the largest proportion of the total churning torque during high-speed operation of the wet motor. Therefore, in future research, how to optimize the structure parameters to reduce the side churning torque is the key issue for the successful application of the wet motor.
This work is supported by the National Key R&D Program of China (No. 2019YFB2005202).
Bin MENG designed the research. Zhenzhou ZHANG and Mingzhu DAI processed the corresponding data. Zhenzhou ZHANG wrote the first draft of the manuscript. Chenchen ZHANG and Yi CHEN helped to organize the manuscript. Bin MENG revised and edited the final version.
Zhenzhou ZHANG, Mingzhu DAI, Chenchen ZHANG, Yi CHEN, and Bin MENG declare that they have no conflict of interest.
Cai XZ, 2018. Analysis on the research status of motor pump at home and abroad., 38(9):1-3 (in Chinese). https://doi.org/10.3969/j.issn.1008-0813.2018.09.001
Chao Q, Zhang JH, Xu B, et al., 2019. A review of high-speed electro-hydrostatic actuator pumps in aerospace applications: challenges and solutions., 141(5):050801. https://doi.org/10.1115/1.4041582
Claar LM, Hodges RC, 1998. Integrated Electric Motor Driven in Line Hydraulic Pump. US Patent 5708311.
Fu YL, Yang JY, Zhu DM, 2017. Finite element analysis of flow field and temperature field of electro-hydraulic pump by Fluent., 43(8):1647-1653 (in Chinese). https://doi.org/10.13700/j.bh.1001-5965.2016.0605
Gao DR, Liu JH, Wen MS, 2010. Analysis of internal flow field of a new axial piston hydraulic motor pump., 34(6):483-492 (in Chinese). https://doi.org/10.3969/j.issn.1007-791X.2010.06.002
Ge YW, Zhu WL, Liu JH, et al., 2021. Refined modeling and characteristic analysis of electro-hydrostatic actuator., 57(24):66-73 (in Chinese). https://doi.org/10.3901/JME.2021.24.066
Huang Y, Ding C, Wang HY, et al., 2020. Numerical and experimental study on the churning losses of 2D high-speed piston pumps., 14(1):764-777. https://doi.org/10.1080/19942060.2020.1763468
Jensen KJ, Ebbesen MK, Hansen MR, 2021. Novel concept for electro-hydrostatic actuators for motion control of hydraulic manipulators., 14(20):6566. https://doi.org/10.3390/en14206566
Ji H, Li ZF, Wang ZR, et al., 2010. Performance test of the prototype of electric motor pump., 41(11):48-51 (in Chinese). https://doi.org/10.3969/j.issn.1000-1298.2010.11.009
Ji H, Zhang JM, Wang JL, et al., 2014. Charging effect of port-plate centrifugal pump in electric motor-pump., 50(10):177-182 (in Chinese). https://doi.org/10.3901/JME.2014.10.177
Jiao ZX, Li ZH, Shang YX, et al., 2022. Active load sensitive electro-hydrostatic actuator on more electric aircraft: concept, design, and control., 69(5):5030-5040. https://doi.org/10.1109/TIE.2021.3084179
Jin DC, Ruan J, Li S, et al., 2019. Modelling and validation of a roller-cam rail mechanism used in a 2D piston pump., 20(3):201-217. https://doi.org/10.1631/jzus.A1800085
Jin ZH, Zhao LY, Zhao XL, 2021. Research on characteristics of oil immersed motor for deep water servo application., 37(3):40-44 (in Chinese). https://doi.org/10.3969/j.issn.1673-095X.2021.03.008
Kittisares S, Hirota Y, Nabae H, et al., 2022. Alternating pressure control system for hydraulic robots., 85:102822. https://doi.org/10.1016/j.mechatronics.2022.102822
Lee YN, Minkowycz WJ, 1989. Heat transfer characteristics of the annulus of two coaxial cylinders with one cylinder rotating., 32(4):711-722. https://doi.org/10.1016/0017-9310(89)90218-4
Lei ZF, Qin LJ, Wu XD, et al., 2021. Research on fault diagnosis method of electro-hydrostatic actuator., 2021:6688420. https://doi.org/10.1155/2021/6688420
Li WF, Liu HF, Gong X, 2016. Engineering Fluid Mechanics. 2nd Edition. East China University of Science and Technology Press, Shanghai, China, p.96-97 (in Chinese).
Li YP, Jiao ZX, Yu T, et al., 2020. Viscous loss analysis of the flooded electro-hydrostatic actuator motor under laminar and turbulent flow states., 8(8):975. https://doi.org/10.3390/pr8080975
Li ZF, Shao YB, Fu YL, et al., 2014. Oil gap loss and mechanical efficiency of axial piston electro-hydraulic pump., 40(6):769-774 (in Chinese). https://doi.org/10.13700/j.bh.1001-5965.2013.0438
Liu J, 2021. Analysis of Cavitating Jet Characteristics of Axial Piston Pump Considering Viscosity Temperature Characteristics. MS Thesis, Taiyuan University of Technology, Taiyuan, China (in Chinese). https://doi.org/10.27352/d.cnki.gylgu.2021.000756
Nouri-Borujerdi A, Nakhchi ME, 2017. Heat transfer enhancement in annular flow with outer grooved cylinder and rotating inner cylinder: review and experiments., 120:257-268. https://doi.org/10.1016/j.applthermaleng.2017.03.095
SAUER BIBUS, 1999. Electrical Motor with Integrated Axial Piston Pump Series J-RP Rotor Pump. https://www.sauerbibus.de/fileadmin/editors/countries/sab/Downloads/J-RP_007_0605.pdf
Song BC, Lee DY, Park SY, et al., 2019. Design and performance of nonlinear control for an electro-hydraulic actuator considering a wearable robot., 7(6):389. https://doi.org/10.3390/pr7060389
Taylor GI, 1923. VIII. Stability of a viscous liquid contained between two rotating cylinders., 223(605-615):289-343. https://doi.org/10.1098/rsta.1923.0008
Wang H, Cao C, Guo J, et al., 2022. Design and friction loss study of full-ocean depth oil-filled direct current motor., 23(8):587-598. https://doi.org/10.1631/JZUS.A2100375
Wang Y, Guo SR, Dong HK, 2020. Modeling and control of a novel electro-hydrostatic actuator with adaptive pump displacement., 33(1):365-371. https://doi.org/10.1016/j.cja.2018.05.020
Wu Y, Xi WJ, Zhang CL, et al., 2022. Thermohydrodynamic lubrication analysis of micro gas bearing with journal misalignment., 37(9):1979-1991 (in Chinese). https://doi.org/10.13224/j.cnki.jasp.20210209
Zhang CC, Ruan J, Xing T, et al., 2021. Research on the volumetric efficiency of a novel stacked roller 2D piston pump., 9(7):128. https://doi.org/10.3390/machines9070128
Zhang DJ, Gao DR, Wang YJ, et al., 2008. Numerical calculation and analysis of electro-magnetic field of axial piston hydraulic motor pump based on ANSYS., 44(12):69-74 (in Chinese). https://doi.org/10.3901/JME.2008.12.069
Zhang Y, 2020. Research on the Operating Characteristics and Structure Influence of the Rotary Energy Recovery Device. MS Thesis, Jiangsu University, Zhenjiang, China (in Chinese). https://doi.org/10.27170/d.cnki.gjsuu.2020.001417
Zhang YY, 2022. Thermal-Hydraulic Modeling and Structure Optimization of Oil-Immersed Motor Pump. MS Thesis, Yanshan University, Qinhuangdao, China (in Chinese). https://doi.org/10.27440/d.cnki.gysdu.2022.001234
Zhu BH, Qian PC, Ji ZQ, 2018. Research on the flow distribution characteristics and variable principle of the double-swashplate hydraulic axial piston electric motor pump with port valves., 54(20):220-234 (in Chinese). https://doi.org/10.3901/JME.2018.20.220
Zhu T, Xie HB, Yang HY, 2022. Design and tracking control of an electro-hydrostatic actuator for a disc cutter replacement manipulator., 142:104480. https://doi.org/10.1016/j.autcon.2022.104480
Zhu YC, Xiao QH, Gao MX, et al., 2018. Flow characteristics analysis of a two-phase suspension between rotating porous cylinders with radial and axial flows., 22(4):1857-1864. https://doi.org/10.2298/TSCI1804857Z
Zou GW, He Z, Gu X, 2013. Viscous Fluid Dynamics. National Defense Industry Press, Beijing, China, p.215-219 (in Chinese).
湿式三相高速磁阻电机搅拌损失的特性研究
张震舟,戴铭柱,张晨晨,陈义,孟彬
浙江工业大学,机械工程学院,中国杭州,310023
传统干式电机在高速工况下存在动密封磨损和油液泄露等问题。1. 本文通过电机湿式化提出一种湿式三相高速磁阻电机泵的新结构以去除动密封。2. 简化电机泵结构并提高集成度,以通过油液的循环流动改善电机散热问题。3. 集中研究电机湿式化后所引起的搅拌损失问题,为后续湿式电机搅油阻力矩的减阻优化提供一种较好的计算方法。
1. 提出一种新型湿式三相高速磁阻电机泵,并通过O型密封圈来构成湿式耐高压结构,避免了高速工况下的动密封磨损、油液泄露和发热严重等问题;2. 通过理论分析,推导出湿式电机搅油阻力矩的解析模型;3. 基于计算流体力学(CFD)建立湿式电机搅油的仿真模型,并对其运行过程中所受到的阻力矩和内部流场状态进行分析;4. 设计制造实验样机,搭建湿式电机搅油的实验台架,并测试不同转速和温度下的搅油阻力矩。
1. 通过理论分析,建立湿式电机搅油阻力矩的解析模型(公式(26));2. 通过仿真模拟,对电机运行过程中内部流场状态(图9和10)与其受到的流体阻力矩(图11和12)进行分析,验证解析模型的有效性(图13和14);3. 通过湿式电机搅油样机和实验台架(图15和16)测试不同转速和温度下的搅油阻力矩,验证解析模型和仿真模拟的有效性(图19和20)。
1. 湿式三相高速磁阻电机泵的新结构能够去除传统动密封,使其无需克服动密封摩擦力;这大大简化了电机泵的结构,提高了集成度,使其可通过油液的循环流动改善电机散热问题。2. 电机搅油阻力矩与内部流场参数之间存在映射关系,因此可通过建立解析模型实现关联表征;通过CFD对湿式电机搅油进行仿真模拟,能够验证解析模型的有效性,为电机流场求解提供一种较好的方法。3. 实验结果验证了解析模型和仿真模拟的有效性;三者的搅油阻力矩在不同转速、不同温度下的曲线趋势吻合良好,为后续湿式电机搅油阻力矩的减阻优化提供了一种较好的计算方法。4. 在高速运转过程中,电机的侧面搅油阻力矩占总搅油阻力矩的比重很大,所以如何优化电机结构参数以减小其侧面搅油阻力矩是该湿式电机能否得以成功应用的关键所在。
电机泵;湿式电机;搅拌损失;解析模型;计算流体力学(CFD)
https://doi.org/10.1631/jzus.A2300053
https://doi.org/10.1631/jzus.A2300053
Received Jan. 30, 2023;
Revision accepted June 8, 2023;
Crosschecked Dec. 12, 2023
© Zhejiang University Press 2024
 Journal of Zhejiang University-Science A(Applied Physics & Engineering)2024年3期
Journal of Zhejiang University-Science A(Applied Physics & Engineering)2024年3期
- Journal of Zhejiang University-Science A(Applied Physics & Engineering)的其它文章
- Recent progress in the development of dielectric elastomer materials and their multilayer actuators
- Non-uniform thermal behavior of single-layer spherical reticulated shell structures considering time-variant environmental factors: analysis and design
- Synthesis and characterization of three new solid polyoxometalates based on Wells-Dawson-derived sandwich-type polyanions Co4(H2O)2(P2W15O56)2]16-
- Development of underwater electric manipulator based on interventional autonomous underwater vehicle (AUV)
- A method for support stiffness failure identification in a steel spring floating slab track of urban railway: a case study in China
