基于POD和DMD的60°交叉管绕流分析

张 嶔，杨青青，唐也婷，王天源

（中国海洋大学工程学院，山东青岛 266100）

0 引 言

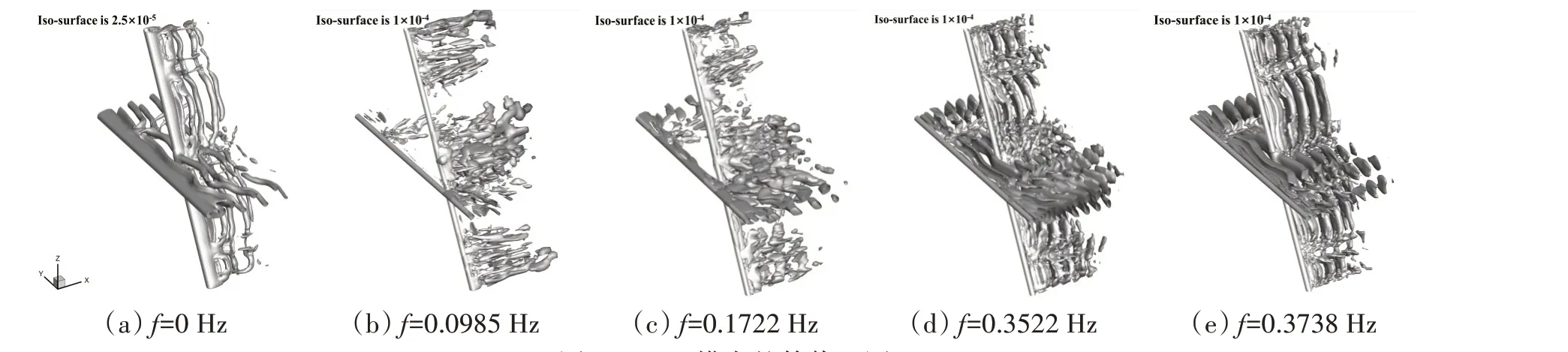
圆柱绕流作为流体力学中的经典问题，在工程应用领域十分广泛，如热力管道、桩基础及风或水流中的桁架结构等。当流体流经圆柱表面并从边界层分离，随之产生的涡脱落现象是导致尾流场复杂的主因。而雷诺数Re是影响圆柱尾流形态的关键因素。Zdravkovich[1]通过实验发现：单圆柱尾涡形态随雷诺数Re改变明显，圆柱尾涡在40

传统的涡识别方法（如Q 准则、λ2方法[5]等）呈现的流场具有时空耦合性，尤其对于严重失稳的流场，在小尺度涡结构的干扰下难以捕获主导流场演变的关键流态。针对传统涡识别方法的局限性，诸如本征正交分解（POD）[6-7]和动力学模态分解（DMD）[8]等降阶模型（ROMs），可分别从空间正交性和频率独立性角度降维分解复杂流场并提取关键模态信息。

王智慧等[9]利用DMD 提取了椭圆柱尾流中的相干结构，结果表明大振幅模态包含了流场的主要信息。孙婉容等[10]利用DMD重建单、双圆柱流场时发现，模态分解结果和重建精度取决于数据量。袁猛等[11]利用DMD 方法分析并列双圆柱尾流场的涡量数据，发现增加奇异值的截断阶数并不能对流场预测效果起到积极作用。Sakai 等[12]利用POD 和DMD 分析了单、串联及并排圆柱尾流，发现间隙比G影响尾流模态的对称性。Bai等[13]通过POD对比了波形和光滑圆柱的三维POD模态特征，发现仅凭少量低阶模态便可近似重建尾流场。Sirisup 等[14]提取了交错圆柱三维尾流场的主导POD 模态，并探究了上、下游圆柱尾流形态对温度场分布的影响。现阶段，POD 和DMD 常用于分析二维圆柱尾流，尚未涉及三维交叉管算例。基于张嶔等[15]通过直接数值模拟（DNS）获取的数值结果，本文利用POD 和DMD对比分析60°交叉管在Re=200、G=4下的涡量数据以探究其尾涡演变规律。

1 模态分解方法

POD[6，7]和DMD[8]可通过降维分解方式识别时空耦合尾流场无法呈现的流动信息，本章简要回顾了POD和DMD的基本理论，具体理论可见相应引用文献。

1.1 POD方法

POD 本质上是对快照矩阵X的空间协方差矩阵R=XXT执行特征值分解（EVD）以寻求可最佳表示给定流场数据的基函数，等同于在最小二乘意义上对快照矩阵X执行奇异值分解（SVD）：

1.2 DMD 方法

Schmid[8]提出的DMD理论假设相邻快照之间存在一个时间不变线性算子A，在离散时间的动力学系统中表示为

式中，A∈ℂn×n，†表示Moore-Penrose伪逆，相当于在最小二乘意义下寻求矩阵A的最佳拟合解。

与POD 不同，DMD 假设流场的模态和动力学信息分别包含在算子A的特征向量和特征值中。由于矩阵A一般过大，直接对矩阵A执行EVD 需大量的内存资源，因此通常采用Tu 等[16]提出的DMD 算法以降低计算成本，最终可得各DMD模态及其振幅（能量）αi、增长/衰减率gi及频率fi等信息。

2 算例概述

2.1 模型建立

本文选用三维（3D）Navier-Stokes（N-S）方程，流体运动粘性系数ν=0.005 m2/s，雷诺数Re=UxD/ν=200，流场处于过渡阶段[17]。

如图1 所示，所选研究对象为直径D=1 m，长度为40D的交叉布置双管，其中上游圆柱（UC）水平布置，下游圆柱（DC）按一定间隙比G=L/D（L为两圆柱外径间隙长度）倾斜60°布置。计算域长、宽、高分别为（32+G）D、40D、40D。

图1 60°交叉双圆柱计算域示意图[15]Fig.1 Schematic diagram of two cylinders in 60°crossing arrangement and computational domain[15]

2.2 频谱及瞬时流场

在确定计算模型及网格（图2）后，基于OpenFOAM 的有限体积法，对交叉双管（60°，G=4）在雷诺数Re=200下进行直接数值模拟DNS。计算时间步长为dt=0.01 s，在流场稳定的第400 s后开始输出涡量数据以作后处理。图3展示了420 s瞬时时刻的涡量等值面及其在z=0平面上的云图。对20 s（400～420 s）内上游UC 及下游DC 圆柱的升力系数进行快速傅里叶变换（FFT）以计算其频谱，结果如图4 所示。UC 及DC 的频谱峰值主要集中于0.19 Hz 附近，即上下游圆柱的涡脱落周期约为5.26 s。由于UC 涡脱落对DC 造成影响，导致两者频谱峰值略有差异。UC 频谱相对光滑，但DC 在来自UC 的涡脱落影响下于0.09 Hz、0.28 Hz、0.38 Hz 和0.49 Hz 附近出现频谱峰值。

图2 交叉管（60°，G=4）在z=0平面上的网格划分Fig.2 Computational mesh around two crossing cylinders in 60°,G=4 on the z=0 plane

图3 基于合涡量展示的60°交叉管附近的流动Fig.3 Flow around two crossing cylinders in 60°arrangement based on vorticity magnitude

图4 交叉圆柱的升力频谱图Fig.4 Spectra of lift coefficients on upstream and downstream cylinders

2.3 模态收敛性分析

数据集收敛性涉及快照采样频率（采样时间间隔的倒数）和数量两个参数，完整的数据集既要确保低频（大周期）流动现象完整呈现，又要不缺失高频流动现象。据Nyquist-Shannon采样准则，POD和DMD所能捕获的流体最大频率fmax为快照采样频率fsamp的一半，即

鉴于快照采样频率为fsamp=100 Hz，最大捕获频率fmax=50 Hz，设置不同时间间隔Δt=[0.01，0.02，0.03，0.04，0.05]s（可依次捕获50 Hz、25 Hz、16.67 Hz、12.5 Hz 和10 Hz 频率范围内的模态）和快照数量m=[100:100:2000]以研究其对模态收敛性的影响。

由图4可知，上下游圆柱的升力频谱峰值约为0.19 Hz，故本文针对不同时间间隔和快照数量统计0.19 Hz 附近DMD 模态的增长率，频率误差保持在10%以内则予以考虑。统计结果（图5）表明，Δt=0.01 s、0.02 s和0.03 s分别在m=100～300，100～200和100未捕获到0.19 Hz附近的模态，说明数据集至少需覆盖一个涡脱落周期（5.26 s）。在完整覆盖一个涡脱落周期后，模态增长率趋于收敛并不再受时间间隔影响。最终，在计算资源允许范围内，本文选择时间间隔Δt=0.01 s 和快照数量m=2000的数据集，该数据集可捕获0～50 Hz范围内及约3.8个涡脱落周期内的2000个流动模态。

图5 模态收敛性分析Fig.5 Analysis of modal convergence

3 模态分解结果

3.1 POD统计分析

图6展示了前25个POD 模态的能量占比E（i式（3））和累积能量占比Eicum（式（4））。其中第1阶模态能量占比最高，占流场总能量的68.57%；第2、3 阶和第4、5 阶模态能量成对相同，呈“阶梯”状下降特征；随着模态阶数的增加，相邻模态能量不再成对相同，且能量占比均低于1%。此外，累积能量占比分布表明，仅需15个模态便可捕获90%的流场总能量。

图6 POD模态能量占比及累积能量占比Fig.6 Energy proportion and cumulative energy proportion of POD modes

图7展示了前100阶POD模态的频谱分布，其中频谱峰值作归一化处理并由黑色像素点代表。统计结果表明，模态频谱峰值为模态阶数的线性函数。综合图6和图7可知，低阶POD模态对应高能、低频流动现象；反之，高阶POD模态则对应低能、高频现象。

图7 POD模态频谱分布Fig.7 Spectrum of POD modes

3.2 DMD统计分析

为避免大振幅但高衰减率的DMD 模态影响分析，选择振幅绝对值除以增长/衰减率绝对值|αi|/ |gi|以衡量DMD 模态对尾流动力学的贡献程度。图8（a）展示了排除零频f=0 Hz 模态后 |αi|/ |gi|关于频率fi的归一化统计结果，图8（b）进一步将 |αi|/ |gi|作为模态的排序标准对每一DMD 模态染色以统计模态增长率gi关于频率fi的统计结果，排序越靠前的模态颜色越深。

图8 DMD模态的频谱Fig.8 Spectra of DMD modes

由图8（a）可知，f=0.1861 Hz 模态对流场的贡献程度最高，该频率接近上、下游圆柱涡脱落频率0.19 Hz，其次，f=0.0985 Hz、0.1722 Hz、0.3522 Hz、0.3738 Hz 等模态也相当重要。由图8（b）可知，模态的重要程度（颜色）随频率增加而减弱（变浅）。对比图7可知，POD模态具有多频性，而DMD模态则具有单频特性。

3.3 模态分析

由上、下游圆柱的升力频谱（图4）、POD 频谱（图7）和DMD 频谱（图8）可知，主导（第2、3 阶）POD模态及主导（f=0.1861 Hz）DMD模态均强调f≈0.19 Hz附近的模态，图9与图10展示了第2阶POD模态及f=0.1861 Hz时DMD 模态的实部。由三维等值面（图9）可知，两模态的空间形态相似，主要表征上、下游圆柱的P形态涡脱落现象（Zhao[4]及张嶔[15]）。

图9 POD和DMD模态的等值面图Fig.9 Iso-surfaces of POD and DMD modes

图10 POD和DMD模态在z=0平面上的云图Fig.10 Contours of POD and DMD modes on the z=0 plane

图11（a）进一步对比了第2、3阶POD模态和f=0.1861 Hz时DMD模态实部及虚部的时间系数。可以看出，第2阶POD模态与DMD模态实部、第3阶POD模态与DMD模态虚部的振荡频率相同，两者间存在一定相位差。图11（b）分别利用第2、3阶POD模态和f=0.1861 Hz处DMD模态实部及虚部的时间系数绘制了相位轨迹图，表现为不同半径的同心圆，说明时间系数为存在90°相位差的正弦曲线，而半径差异与时间系数的不同振幅有关。POD 轨迹为非规则圆，主要由时间系数的振荡引起，DMD 轨迹为螺旋圆，螺距表征衰减率gi。

图11 POD和DMD模态关于时间系数的对比Fig.11 Comparisons of time coefficients between POD and DMD modes

POD 从空间正交性角度分解模态，而DMD 则基于频率独立性，因此POD 模态多以多频耦合形式出现，而DMD 模态始终具有单频特性。POD 可将周期性流动现象分解为空间形态相似且能量相同的一组模态对，对应图6 中第2、3 阶模态的阶梯状能量分布。该模态对具有单频性，且二者时间系数间存在90°相位移（Dietmar 和Fasel[18]）。若流动现象由于尾流失稳而丧失周期性或周期性减弱，则相邻POD 模态的空间形态与能量便不再成对相同（如第6、7阶模态），且其时间系数存在波动，导致POD 模态具有多频性（图7）。此外，Schmid 等[19]的研究表明，对于周期性流动现象，复DMD 模态的实部和虚部可由一组同频POD模态ui+iui+1表示，但对于非周期性流动现象没有同等表示。

鉴于POD 模态和DMD 模态的空间特征类似，且DMD 模态的单频特性便于流体机理的分析，故下面将展示其他具有典型特征的DMD模态。

DMD 频谱（图8）中存在衰减率及频率均为0的模态，由图12（a）及图13（a）可知，该模态主要表征尾流场中的平均涡量分布，对尾流动力学没有贡献。随着频率的增加，f=0.0985 Hz 和0.1722 Hz 模态（图12（b）～（c）和图13（b）～（c））与下游圆柱的大尺度流向涡有关，而f=0.3522 Hz和0.3738 Hz模态（图12（d）～（e）和图13（d）～（e））与全局跨向涡脱落有关。经对比，模态的空间尺度随频率的增加而减小。图14进一步展示了上述模态的时间系数，其包络线斜率与模态衰减率（图14（b））有关。

图12 DMD模态的等值面图Fig.12 Iso-surfaces of DMD modes

图13 DMD模态在z=0平面上的云图Fig.13 Contours of DMD modes on z=0 plane

图14 DMD模态的时间系数演变Fig.14 Time coefficients evolution of DMD modes

3.4 降阶模型

基于上述分析，利用f=[0，0.0985，0.1722，0.1861，0.3522，0.3738]Hz 等模态对尾流场进行低阶重建，结果如图15 所示。与f=0.1861 Hz 模态（图9（b）和图10（b））相比，f=[0.0985，0.1722，0.3522，0.3738]Hz 模态丰富了交叉点后下游圆柱的流向涡演变及远离交叉点处连接相邻平行P 形态跨向涡的流向二次涡。

图15 基于主导DMD模态的重建尾流场Fig.15 Reconstructed wake field based on dominant DMD modes

4 结 论

本文基于张嶔等[15]通过DNS模拟的60°交叉管在间隙比G=4和雷诺数Re=200下的涡量数据，利用POD和DMD两种模态分解方式分析了尾涡的演变规律，得到以下结论：

（1）POD 和DMD 模态的重要性和空间尺度随频率的增加而减小，其中大尺度尾涡可由极少数低频DMD模态重建，而高频模态则表征小尺度流动形态；

（2）上、下游圆柱的平行P 形态涡以0.19 Hz 附近的频率从上、下游圆柱脱落，并按照相同的频率向下游演变，直至破碎；

（3）下游圆柱上的多个高频升力频谱峰值由来自上游的脱落涡和下游圆柱相互作用引起，并最终导致下游圆柱出现涡激振动现象。