基于iFEM 和虚实结合的加筋板应变场构建研究

陈国材，汪雪良，2，杨华伟，2，蒋镇涛，2，张 涛，2，张 正

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082；3.武汉理工大学，武汉 430070）

0 引 言

船舶在长期服役过程中，遭受风、浪、流多种复杂载荷的作用，极易发生结构疲劳损伤，从而导致船体安全性能下降，通过船体监测系统能够感知船舶结构自身安全，实现对船舶结构健康状态的把握[1]。应变作为结构最常采集的物理量之一，同时也是评价船体结构健康状态的重要依据，通常以实际的离散应变测点为基础，开展对结构的全局应变场构建。目前，国内外比较成熟的应变场重构方法有模态法[2-4]、Ko 等人提出的位移理论[5-6]、人工智能[7]和iFEM 法[8-9]等。模态法的核心思想是将结构变形视为各阶模态的线性组合，其重构精度受模态分析精度影响较大；Ko 的位移理论是基于挠度曲线推导的，所以只适用于重构单方向结构变形[10]；人工智能的方法主要基于人工神经网络模型，变形重构模型与被测物的材料属性、结构参数以及环境载荷的分布形式关联性弱，具有较强的通用性，但其重构位移的精确性严重依赖于训练网络时所使用载荷集的丰富性[11]；iFEM 通过构建实测应变值与理论值之间的最小二乘误差函数，结合形函数矩阵与几何矩阵，组装成结构全局应变场，iFEM 能摆脱传统重构方法的局限性，忽略结构的材料属性和受载荷情况，具有较高的工程应用前景。自2003年Tessler[12]正式提出iFEM 的概念和理论以来，国内外学者针对板、梁、壳等结构开展了深入研究，并在机翼、船体等结构健康监测，复合材料变形场重构等领域进一步验证了iFEM的鲁棒性和可行性[13-14]。

重构方法的精度通常正相关于应变传感器布置数量，但是实际工程应用中无法通过布置大量传感器来提升应变场的重构精度，主要有以下原因：一是特殊位置不满足工程施工条件，如结构角隅处等；二是传感器数量的增加，将造成系统成本的上升和可靠性的下降。

面对重构精度提升与降低传感器数量的矛盾，本文提出以虚拟应变传感器和物理传感器虚实结合的应变采集方法。所谓虚拟应变传感器，是指利用数值分析方法给出结构目标位置在不同受载条件下的应变响应，以替代物理应变传感器的技术手段。在iFEM 技术框架下，通过对船舶结构的典型组成单元加筋板布置虚拟应变传感器进行应变场重构，可突破少量物理测点难以实现应变场重构的困境，为全船结构应变场重构提供有效方法。

1 船舶加筋板应变场重构理论框架

在iFEM 技术框架下的应变场构建流程可概括为“两支一主”，“两支”为根据逆壳单元构建单元理论应变和根据物理模型采集的实测应变，“一主”则是构建关于单元节点位移的最小二乘误差函数，对误差函数求极值后，求得单元节点位移，再结合单元几何矩阵组装总体矩阵得到应变场，简化求解流程，如图1所示。

图1 iFEM求解流程Fig.1 Solution process of iFEM

为了适应不同的结构形式和物理模型，需要构建不同的逆向单元，由于加筋板模型是应变呈线性变化的板壳结构，并考虑剪切变形对结构的影响，故采用iQS4 作为逆壳单元和Mindlin 板理论进行应变场重构[15]。如图2所示建立一个板单元的局部坐标系（x,y,z），坐标原点位于板单元的中性面形心处。u、v和w分别是该局部坐标系下x、y和z方向的位移，θx、θy和θz分别为绕x、y和z轴方向的转角。单元厚度为2h，点1、2、3、4分别为单元的4个节点。

图2 四节点逆壳单元iQS4Fig.2 Four-node inverse shell unit iQS4

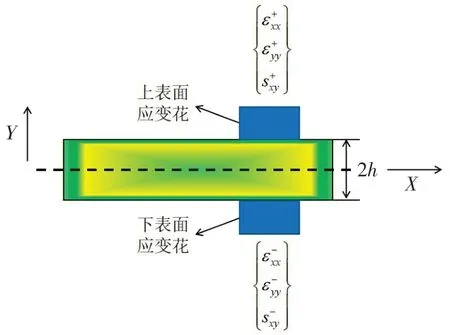
图3 通过iQS4内的应变花测量的离散表面应变Fig.3 Discrete surface strain measured by strain flower in iQS4 element

式中：u0、v0和w0分别表示节点在x,y,z方向上的位移；θx0和θy0表示中线面上一点绕x轴和y轴方向旋转的角度，其中z方向的位移w沿板厚方向基本不变，z∈[-h,+h]。

根据求解流程及有限元理论，四节点单元的形函数如式（2），单元的每个节点可表示为式（3）：

则四节点单元位移矩阵可表示为

根据线弹性理论，加筋板结构某单元的理论应变可大致分为面内的拉压应变e(ue)、弯曲应变k(ue)、剪切应变s(ue)的线性组合，分别如式（5）～（7）所示。

另外，可通过形函数的偏导数矩阵建立起理论应变与单元节点位移矩阵的关系，即加筋板结构的表面应变εb可以用四节点逆壳单元形函数的偏导数矩阵Bm、Bk与单元节点位移矩阵ue表示为

同样，横向剪切应变εs也可以表示为四节点逆壳单元形函数的偏导数矩阵Bs与单元节点位移矩阵ue的乘积，

形函数偏导矩阵Bm、Bk、Bs的详细计算过程及原理见文献[8]。

构建实测应变与理论应变之间的最小二乘误差函数，然后求误差函数对单元节点位移的偏导，当误差函数为0时，取得理论上该单元各节点的位移值，并认为此时的单元各节点位移分布对应此时实测应变状态下的实际位移分布。

式中，e(ue)、k(ue)、s(ue)是由中性面位移场表示的单元理论拉压、弯曲、剪切应变；ec、kc、sc是通过仿真试验或者应变片测量得到表面应变信息推导得到的中性面的拉压、弯曲、剪切应变；we、wk、ws为无量纲加权系数，与各截面应变相关，控制着理论中性面应变与实际中性面应变的强弱关系。如果通过应变片或者光纤光栅测量的表面应变信息，可以得到所有单元的中性面应变ec、kc和sc，那么加权系数可取we=wk=ws=1，对于缺失实际中性面应变的情况，如上述中的剪切应变，可以通过调整对应的系数来控制结果的精度以及合理性[10，16]。经过对加筋板某板构造及材质的综合分析，取ws=λ=10-3，其中0<λ≤1，λ为罚参数[16]。

式中，Ae是板单元内的面积，n为单元内传感器的数量。

对误差函数φe(ue)求关于位移向量ue的偏导，并令偏导等于零，求得误差函数φe(ue)的极小值。

整理上式可得

与有限单元法的单元刚度方程类似，式中：ke为单元刚度矩阵，fe为单元载荷矩阵。

矩阵ke由矩阵Bm、Bk、Bs及其对应的加权系数we、wk、ws确定，由于we=wk=1，ws=λ=10-3，具体形式如下：

矩阵fe与矩阵Bm、Bk、Bs及其对应的加权系数we、wk、ws以及应变传感器数量n、单元板厚h有关，由于we=wk=1，ws=λ=10-3，具体形式如下：

组装单元矩阵构建整体矩阵，通过坐标变换矩阵，可将单元在局部坐标系下的刚度矩阵方程转化为在全局坐标系下的刚度矩阵方程，进而将离散结构的刚度矩阵方程进行整合，得到总体结构的总体刚度矩阵方程，此过程类似于有限元思想[14]。

具体求法与形式如下：

式中，K是总体刚度矩阵，与结构离散的单元位置和数量有关，nel是结构离散的单元数量；U是总体结构位移向量；F是总体载荷矩阵，与结构离散的单元中面应变有关；Te为坐标转换矩阵。而k矩阵是一个对称矩阵，与应变测量值无关，与应变测量点所在逆向单元的单元节点位置和应变测量点位置有关，再结合单元边界条件，系数矩阵k将简化为一个正定矩阵，求逆后可得到单元节点的全局位移U。

在忽略板单元的剪切变形的情况下，利用单元的形函数偏导数矩阵与单元节点位移矩阵，加筋板结构表面应变可表示为

如计入板单元的结构剪切应变，可根据剪切应变与拉压应变的关系，合理取罚参数λ，得到

同样可以经过对离散应变单元的组装后得到全局应变ε。

2 模型分析与试验

2.1 加筋板几何参数和材料属性

加筋板作为船体结构中的主要构件，在保证船体结构强度和刚度的情况下可大幅减轻钢材用量。本文中加筋板模型采用低温船用钢设计，板面以下为“九纵四横”结构，即9 根纵骨，4 根横梁，板面以上布置肋板（如图4所示）。详细尺寸及材料属性见表1。

表1 加筋板几何参数和材料属性Tab.1 Geometric parameters and material properties of stiffened plates

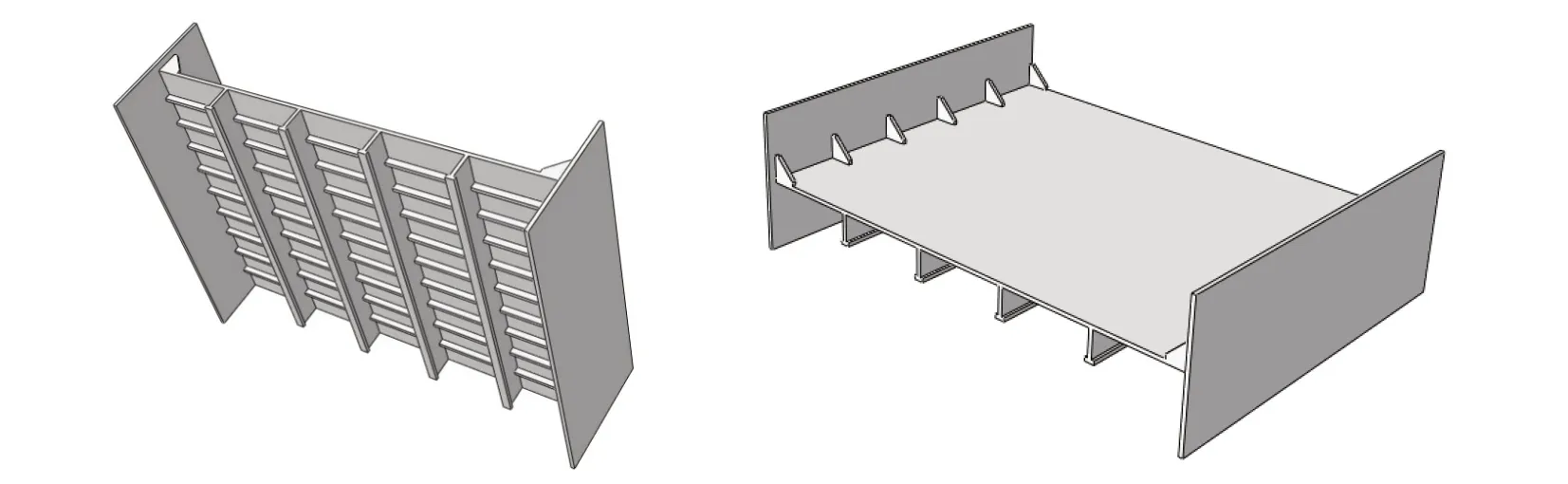
图4 加筋板模型Fig.4 Stiffened plate model

2.2 数值仿真

加筋板以Abaqus 有限元软件进行建模，板、肋板、固定边采用壳单元建模，纵骨横梁采用梁单元建模，共有23 518个单元、71 002个节点，单元均为四边形单元，即为逆壳单元iQS4（如图5所示）。

图5 加筋板有限元模型Fig.5 Finite element model of stiffened plate

为了模拟船舶甲板发生中垂时船舶甲板的载荷响应，试验时采用一端固定，一端加载，固定端边界条件为U1=U2=U3=UR1=UR2=UR3=0，加载端边界条件为U2=U3=UR1=UR2=UR3=0，如图6所示。

图6 加筋板加载示意图Fig.6 Schematic diagram of stiffened plate loading

2.3 模型试验研究

加筋板模型充分考虑了船舶上层甲板建筑物及工程实际，在加筋板边缘布置传感器，以模拟船舶左右舷甲板列板。试验共布置6 个单向应变片、3 个电阻传感器和3 个光纤传感器，本文内容仅用到6 个单向应变片，E1、A1、E3、A2 距最近的固定边15 cm，E2、E4位于加筋板长度方向的对称线上，所有测点均距加筋板边缘2 cm，加筋板试验模型如图7所示。

图7 加筋板模型试验Fig.7 Stiffened plate model test

试验过程中，不可避免地存在应变片粘贴位置不够精确、粘贴工艺不完全相同等状况。以应变片粘贴最终位置为准，在有限元模型中选取相对应位置的单元，使数值仿真与试验保持一致，如图8 所示。实测点与有限元单元号对应表如表2所示。

表2 实测点与单元号对应表Tab.2 Measuring points and corresponding unit numbers

图8 加筋板测点布置示意图Fig.8 Schematic diagram of measuring point arrangement of stiffened plate

试验过程中，先以100 kN为阶梯加载至1400 kN后，再以200 kN为阶梯加载至2000 kN，如此加载重复两次，应变数据基本吻合，工况如表3所示。

表3 加筋板加载工况Tab.3 Loading condition of stiffened plate

由于物理测点有限，基于有限测点难以开展高精度应变场重构工作，针对以上困境开展了Xgboost和虚实结合两种数据补充方法的研究。

3 实测数据分析与处理

将相同位置应变值的实测结果与仿真结果进行对比，并作误差曲线，如图9 所示。E1 点误差较大，其它测点趋势相同，6个测点均随着载荷增大，误差逐渐减小。E2点实测值和仿真值最为接近，除起始工况外，其它工况误差值保持在1.5%～6.7%之间。A1 点和E1 点、E2 点和E4 点、A2 点和E3 点两两形成对照，实测值均有一定差异。另外，实测应变初始值基本不为零，原因有以下几点：一是加筋板在加工过程中存在焊缝不均匀，板内存有内应力等；二是加载过程存在载荷分布不均匀，导致对应点应变值偏差；三是施工工艺不稳定或存在零点漂移，当载荷为零时，5 个测点出现非零值；四是环境因素，试验室中的温度变化，其它机械振动等因素也会对应变采集系统产生影响[17]。综合实测数据分析，试验值和仿真值数据较为接近，此次试验仿真值具有较高参考价值。

图9 加筋板试验、仿真载荷-轴向应变图Fig.9 Test and simulation load-axial strain diagram of stiffened plate

4 虚实结合思路及验证研究

由于此次轴向压缩最大加载为2000 kN，轴向应变值最大，此工况下最接近结构的破坏状态，且具有较高的工程研究意义，故对该载荷作用下的轴向应变场进行重构研究，对6个测点位置分析后，分为4个反演点、2个验证点，如表4所示。

表4 测点分类Tab.4 Classification of measuring points

将板面按照物理区域划分为反演点区域和验证点区域，两者沿加筋板板面对角线对称，反演点区域包含4个反演点，验证点区域包含2个验证点，如图10所示。

图10 反演点、实测点分布图Fig.10 Distribution of inversion points and measured points

基于iFEM 框架，用实测点、虚拟点、虚实结合点三种路径分别对加筋板进行应变场构建，并用E1点、E2 点进行精度验证，由于iFEM 法需要测点上下表面的三向应变，其它方向应变由仿真中的虚拟应变传感器提供补充数据，流程如图11所示。在实测点反演路径中，仅使用4个反演点进行应变场构建，另外采用Xgboost 的回归方法对实测点进行补充，验证并对比三种方法的精度。在虚拟点反演路径中，使用有限元仿真值进行反演，在虚实结合路径中，以4 个实测点补充部分虚拟点再进行反演并构建加筋板应变场。

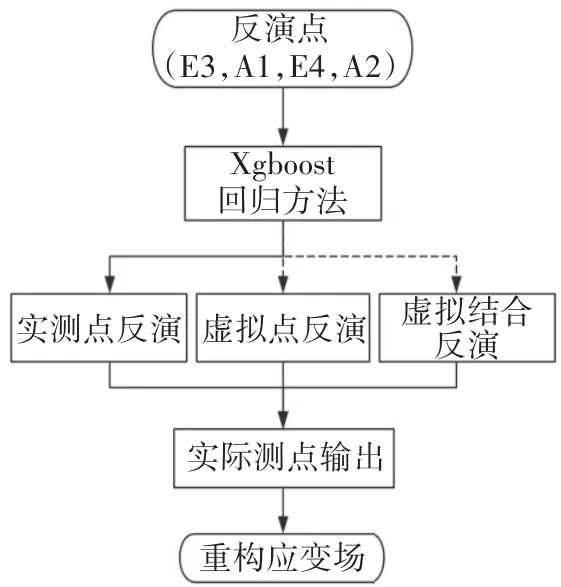
图11 虚实结合方法验证路径Fig.11 Verification path of virtual-real combination method

4.1 15个重构点

以15个测点为输入（I），iFEM 重构值（O）与输入的轴向应变误差曲线如图12所示，实测、虚拟、虚实结合3种路径的平均误差（δ）分别为1.82%、1.09%和1.8%，验证点E1和E2的相对误差见表5。

表5 15个重构点相对误差Tab.5 Relative errors of 15 reconstruction points

图12 15个点I-O-δ图Fig.12 I-O-δ of 15 points

依据实测点、虚拟点、虚实结合点3种路径构建实测应变场和重构应变场，如图13所示，图中（a）、（b）、（c）分别为3种路径构建的实测应变场，（d）、（e）、（f）分别为3种路径的重构应变场。

图13 15个点应变云图及iFEM应变重构云图Fig.13 Strain nephogram and iFEM strain reconstruction nephogram of 15 points

4.2 21个重构点

以21个测点为输入，iFEM 重构值与输入的轴向应变误差曲线如图14所示，实测、虚拟、虚实结合3种路径的平均误差（δ）分别为0.47%、2.1%和2.11%，验证点E1和E2的相对误差见表6。

表6 21个重构点相对误差Tab.6 Relative errors of 21 reconstruction points

图14 21个点I-O-δ图Fig.14 I-O-δ diagram of 21 points

依据实测点、虚拟点、虚实结合点3种路径构建实测应变场和重构应变场，如图15所示，图中（a）、（b）、（c）分别为3种路径构建的实测应变场，（d）、（e）、（f）分别为3种路径的重构应变场。

图15 21个点应变云图及iFEM应变重构云图Fig.15 Strain nephogram and iFEM strain reconstruction nephogram of 21 points

5 应变场构建精度影响因素评估

应变场构建精度的影响因素诸多，有可定量分析因素，如输入点的真实度和数量等，有可定性分析因素，如模型加工工艺、试验加载方式、数据采集技术、环境因素等[18]。通过改变定量物理因素和完善优化相关的定性因素可以更好地评估应变场重构精度。

5.1 Xgboost回归方法分析

Xgboost（extreme gradient boosting）方法的原理是建立一个新的决策树模型，该模型正在学习一个新的函数来拟合上次迭代预测的残差。将所有二分树模型的回归值相加，得到最终的回归结果（如图16所示）。本研究中，通过设置二分树的最大深度来限制收敛准则。

图16 Xgboost回归法Fig.16 Xgboost regression method

Xgboost预测残差的目标函数由损失函数和正则化项组成，正则化项为

式中，l(yi,ŷi)为损失函数，Ω(fk)为正则化项，yi为样本，ŷi为yi的预测结果，在本研究中，损失函数为线性函数，如式（28）所示：

在Xgboost 回归方法中，随机选取16、21、30、40、41、…、48、49、50 个点应变数据，依次放入200 kN数据库中，以仿真值为基准，插值21个点的应变。图17为轴向应变在各次插值中的吻合度曲线，在数据库中，有47 个点时对应的插值结果与仿真值误差最小，最小误差为1.92%；当测点超过47 个点时其误差再次变大，出现过拟合现象。

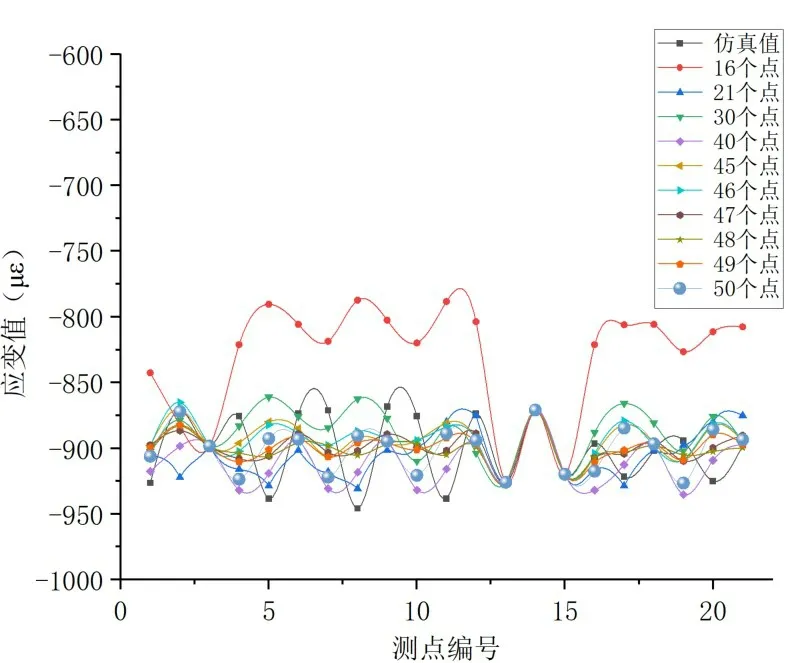
图17 轴向应变吻合度曲线Fig.17 Coincidence cure of axial strain data

在此次加筋板模型中，Xgboost回归方法以仿真与实测值相互补充建立数据库，同样基于此方法，在模型试验时随机物理测点为47 个时，插值误差最小，为1.92%，应变场重构结果最佳。数据量丰盈度与插值精度曲线如图18所示。

5.2 测点数量分析

对此模型9、15、21个测点的情况分别进行了分析研究。通过虚实结合路径，以9个测点构建的结果与验证点E1、E2 的相对误差分别为-2.68%、-4.50%，由于轴向单元划分区域大，且模型边界复杂，重构应变场与实际应变场差距大，本文未做详细分析。以15个测点构建的结果与验证点E1、E2误差分别为2.23%、0.56%。以21个测点构建的结果，与E1、E2验证点误差则分别为1.62%、-2.13%。实测和虚拟路径的重构相对误差如表7所示。

由表可见，虚实结合路径中以15个点和21个点为输入时，其结果与验证点的误差均小于3%。根据应变场重构结果图12和图14，测点为21个点时通过虚实结合路径构建的应变场与实测值构建的应变场更为吻合。

6 结 论

本文基于iFEM 框架以船舶典型结构加筋板为研究对象，在其边缘布置传感器，融入虚实结合思想并结合Xgboost 回归方法，通过对加筋板模型的数值仿真和加载试验，解决了同步提升重构精度与降低物理传感器数量的工程难点，并对试验过程中可能造成重构应变场精度的因素进行了分析。通过研究得出以下结论：

（1）Xgboost 回归方法对于补充实测点具有较高的精确性和实用性，在此模型中，通过预测，当物理测点达到30个时插值结果的平均误差降到2.25%，物理测点达到47个时平均误差最低，为1.92%。

（2）通过虚实结合路径快速补充缺失数据的应变场重构结果操作性强、准确度高，以15个点和21个点为输入时结果与验证点的误差均小于3%。

（3）本文针对加筋板结构提供了一套完整的应变场重构方案，对于相似的板架结构具有一定的参考价值，同时虚实结合路径的验证也为工程应用提供了有效支撑。