一种基于进化策略的气象学反问题求解算法研究

耿焕同,孙义杰,张建,闵锦忠

(南京信息工程大学1.气象灾害省部共建教育部重点实验室;2.计算机与软件学院,江苏南京 210044)

0 引言

气象学中的天气预报是在一定的模式大气条件下,根据初值条件,用数值方法求解模式方程组的过程。造成预报误差的主要原因是初始条件的不准确和预报模式的不准确,因此模式的不断完善和高分辨观测资料的不断利用是推动天气预报发展的主要途径[1-2]。在实际预报业务中,往往先利用已有物理规律和观测资料,对模式参数调整和初始场修正属微分方程组求解中反问题研究范畴;真正作数值天气预报时,实为正问题的求解[3]。

针对数值天气预报中模式参数反演问题,传统方法是通过经验或多次实验去调整参数,因此参数选择必存在一定的随意性和片面性,难以保证所作的调整是有效的;一旦某些参数选择不当,往往会使预报准确率明显降低[4]。其他传统的一些求解反问题的方法存在限制,如增强型拉格朗日法对问题本身有比较苛刻的要求(如连续、可微)[5]。鉴此寻找一种新的适合于气象上的微分方程参数识别反问题求解方法显得十分必要。

随着进化算法理论研究和工程应用的不断深入和发展,进化算法(EA)已成为主要的优化求解方法之一[6-7]。进化算法是一种模拟生物进化规律的搜索和优化计算方法,如遗传算法、进化策略等;此类算法具有很强的通用性、鲁棒性,并且便于并行处理等特点,已被成功应用于机器学习、模式识别、优化控制等领域中[8-9]。同时,在其他工程领域,应用进化算法进行反问题求解已取得许多研究成果[10-11]。

本文利用进化策略在微分方程组反问题求解中的优势,结合气象问题,提出了一种基于进化策略的气象学反问题求解算法,用于预报模式中参数识别及初始条件优化两类反问题的求解中。当利用微分方程作为预报模式进行实际预报时,利用已有观测数据对原模式的参数(或初始场)进行反演以便改善预报水平;最后运用该方法对一维扩散方程和Lorenz-96简单预报模式中反问题进行模拟实验。

1 问题描述

1.1 微分方程反问题

在自然科学和工程应用中,许多模型都可以用微分方程来描述。微分方程的形成和发展是和力学、天文学、物理学,以及其他科学技术的发展密切相关的。通常微分方程的求解是寻找满足定解问题初、边值条件的微分方程的解,又称为正问题。其特点是由“原因”推出“结果”,是自然探索的一种传统途径。微分方程的反问题是指由“结果”推出“原因”。即已知微分方程的解,去求方程中的未知部分。反问题是从各个领域、学科的实际需求中提出的,反问题研究是一门交叉性学科。例如,工程应用中的识别、反演问题就属于反问题的范畴。

1.2 微分方程反问题的分类

设研究的微分方程一般形式如下:

微分方程Ku(x,t)=f(x,t),x∈Ω,t∈(0,∞)。

初始条件Iu(x,0)=φ(x),x∈Ω。

边界条件Bu(x,t)=Φ(x,t),x∈aΩ。

附加条件Au(x,t)=Ψ(x,t);x∈aΩ。

其中:u(x,t)为偏微分方程的解;f(x,t)为右端项;φ(x)、Φ(x,t)、Ψ(x,t)分别为初始条件、边界条件和附加条件。K、I、B、A分别为微分算子、初始算子、边界算子和附加算子。当上述这些已知量中有一个变为未知时,就构成了偏微分方程的反问题。

1)当微分算子K为未知时,称为算子识别反问题。通常情况下算子结构已知,未知的是算子中的参数。这类问题称为参数反演、参数识别问题。在自然科学和实际应用中,这类问题最为常见。

2)当右端项f(x,t)为未知时,称为源的反问题。

3)当初始条件φ(x)未知时,称为初始条件反问题。在附加条件中往往给出系统在某一时刻的状态,即在后某一时刻去确定初始的状态,所以也称为逆时间过程的反问题。

4)当边界条件Φ(x,t)未知时,工程上称为边界控制反问题。

5)当区域的边界aΩ为未知时,称之类问题为几何反问题。工程中的某些定向设计问题常归为这类问题。一维几何反问题是确定端点的位置,二维、三维的反问题则是确定曲线的形状。

2 应用进化策略求解微分方程反问题

2.1 微分方程中的反问题求解到函数优化的转化

以基于以上定义的偏微分方程(除若干参数待调整外)预报系统为例,只要输入初始场及模式参数值,模式即可输出未来某一时刻的预报,以向量Bm表示t=tm时刻的初始场,实向量K表示模式参数,向量Om表示t=tm+τ时刻模式的输出,则预报过程可表示为

若M模式已知,但模式中的参数K未知,即为参数反演问题。利用观测场O(或其中部分元素)的观测值Oob,在参数K的容许区间内找到最佳近似Kbest,使模式输出与相应的观测值之差最小。

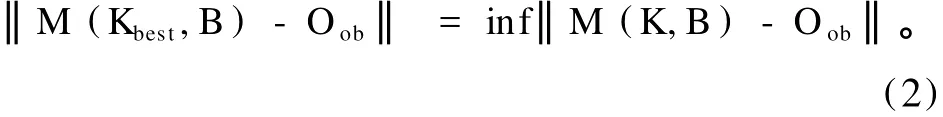
其中:‖‖表示两个向量间的距离函数,将‖M(K,B)-Oob‖作为目标函数,即将参数反演问题转化为函数优化问题,根据提供的观测值对模式中的参数进行调整,力使‖M(K,B)-Oob‖取得最小值,从而得到参数的最优估计值。

若初始场B未知,即为初始场反问题。利用观测场O(或其中部分元素)的观测值Oob在观测变量参数B的容许区间内找到最佳近似初始场(或分析场)Ba,使模式输出与相应的观测误差最小。

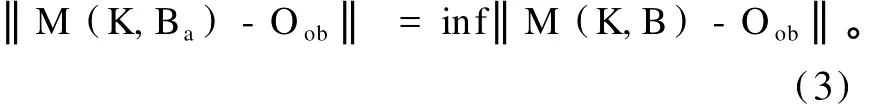
将‖M(K,B)-Oob‖作为目标函数,即将初始场反问题转化为函数优化问题,根据观测值调整参数B,使‖M(K,B)-Oob‖取得最小值时,就得到初始场的最优估计值。若观测变量间需满足协调条件,则可转化为带约束的优化问题,本文暂不作讨论。

综上所述,令目标函数f=inf‖M(K,B)-Oob‖,将反问题的求解等价转化为函数优化问题。即根据所提供的观测资料采用进化策略优化方法,调整模式参数(或初始场Ba)使‖M(K,B)-Oob‖取得最小值,以得到模式参数(或初始场Bm)的最优估计值。

2.2 进化策略

经过从反问题求解到函数优化的转化,首先给出进化策略进行问题求解的框图(图1)和相应的步骤。

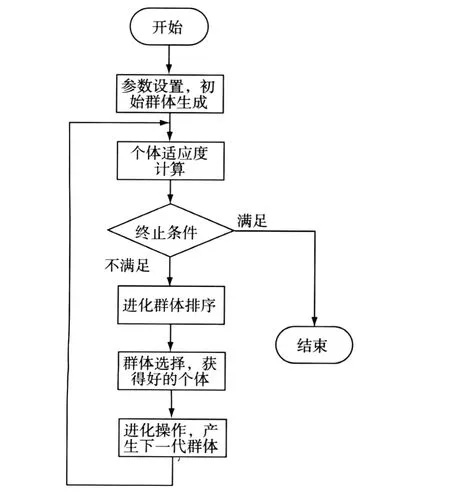
图1 进化策略的算法流程Fig.1 Flowchart of evolutionary strategy algorithm

步骤1:产生初始群体。采用实数编码,随机产生初始群体,设群体规模为μ。

步骤2:计算适应度值。对所有个体将其目标函数作为适应度,适应度函数为f。当最小的适应度值f小于等于一个很接近0的值η时,算法终止。

步骤3:对群体进行排序。所有个体按照适应度值的大小进行排序,适应度值较小的个体排在适应度值较大的个体的前面。

步骤4:选择操作。从步骤3排序完成后的群体中,选取前μ个个体。

步骤5:进化操作。将步骤4中选取的μ个个体作为父代,进行正态分布的变异遗传操作,生成λ个子代;转到步骤2。

用进化策略求解参数反演问题时,根据问题中参数K或B容许区间对参数采取实数编码策略。(1)模式参数优化。通常预报模式已知,但其参数未知,因此需要对其参数优化。设预报模式M中有p个待参数为K={k1,k2,…,kp},反演问题转化为一组最优估计系数Kop,使得目标函数预报误差f取得最小值。(2)初始场优化。在求解初始场反问题时,设待优化的n维初始场B={b1,b2,…,bn}。初始场反问题转化为一组n个初始场中各变量的最优估计,得到初始场B的最优分析场Ba,使得目标函数预报误差f取得最小值。

3 实验与讨论

为了进一步验证基于进化策略的气象学反问题求解算法有效性及其性能,进行了两类数值模拟试验。试验1:是预报模式中的参数识别反演问题,采用预报模式已知、模式参数未知的线性扩散方程进行数值试验[4];试验2:是初始场优化反演问题,用Lorenz-96模式进行数值试验[12]。

3.1 一维扩散方程中的参数反演

考虑如下的问题:

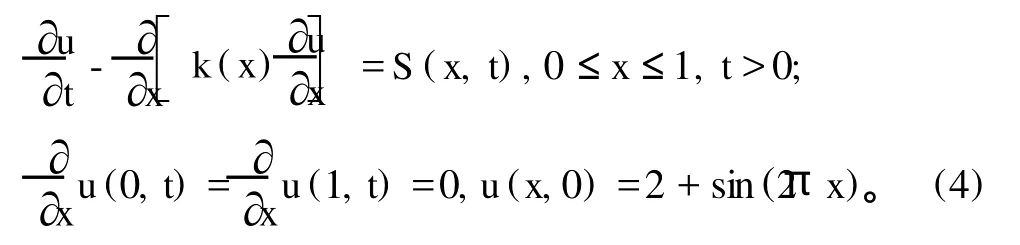
取s=0.05cos(2πx-0.1t),正问题是给出扩散参数k(x)后,用差分方法求出离散解ui,m=u(iΔx,mΔt)。反问题是给出u(x,t)的观测值ui,m,i=0,1,2,…,20,m=50,要求确定扩散参数k(x)。试验中取一般中央差格式,Δx=0.05,Δt=0.01。

试验采用的k(x)的真值如图2所示,有强的间断性。依据文献[4]中对k(x)的估计函数形式

这样问题转化为对a1、a2、a3、b2、b3等5个参数的反演。

为了便于进化计算求解,构造如下目标函数

式中:uob为观测值。此时,就可将参数反演问题转化为下列函数优化问题。若求得解(a1,a2,a3,b2,b3),将其带入式(5)中,得到k＊(x),通过中央差格式求得,使得f=0(或者f为接近0的数),那么k＊(x)为扩散参数的最优估计。

算法在MATLAB7.1上实现,运行参数设置如下:子代规模μ=30、λ=200、pf=0.45,应用ES-(μ,λ)进化策略。为了更好地与真值kT(x)比较,评价指标采用:

统计参数均方误差

经过100代进化得到的参数k(x)的估计值:k＊(x)=0.018 500 5+0.001 285 5cos(2πx)-0.000 004 4cos(3πx)-0.000 006 1sin(2πx)+0.000 561 1sin(2πx)。相应的结果如图2所示,实线表示待定参数k(x)的真值,带点虚线表示通过进化策略算法求得参数k(x)的最优估计值,此时模式预报的均方误差为1.996×10-3。文献[13]中用最优k(x)估计值:k＊(x)=0.018 510 0+0.001 418 4cos(2πx)+0.000 018 8cos(3πx)-0.000 016 7sin(2πx)+0.000 384 1sin(2πx),重新计算得模式预报均方差为2.075×10-3。因此本文通过进化策略求得模式k(x)参数估计值的预报均方差更小。

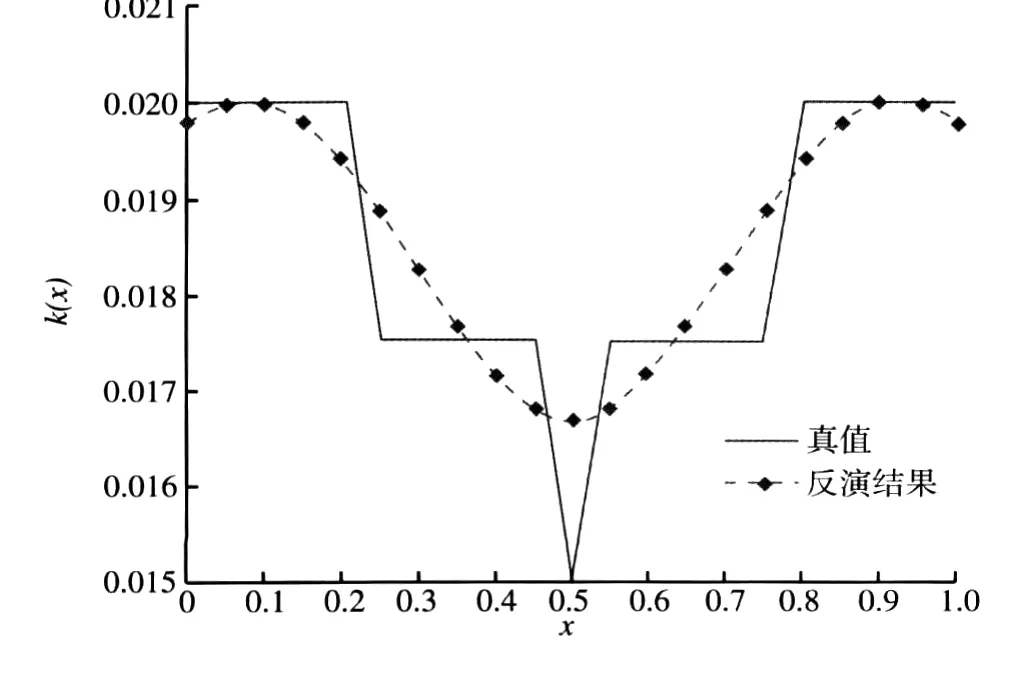
图2 一维扩散方程参数k(x)真值与反演结果Fig.2 Real value and inversion result of parameter k(x)in one-dimensional diffusion equation

3.2 Lorenz-96模式的初始场反演

Lorenz-96模式是LOREN Z和EMANU EL于1996年从动力模式中推导并简化出的新的动力模型,已被广泛用来验证各类同化算法。该模型仍然具有Lorenz模型的特点,对初值极端敏感,且有很强的非线性。该模式是一个可变尺度的低阶动力学系统,模式中包含n个状态变量X1,X2,…,Xn,均匀分布在同一纬圈上。模式的控制方程为

式中:i为循环标号;参数F=8;n一般取40。正问题是确定一组初始状态变量X1,X2,…,Xn,通过差分格式求解T时刻的状态变量。反问题是给出T时刻的状态变量,要求确定初始状态变量X1,X2,…,Xn。使用4阶Runge-Kutta差分格式来求解该模式,时间步长t=0.05[13],T=mΔt,m取20。

显然若求得解Y=(Y1,Y2,…,Yn),将其代入式(7),通过4阶Runge-Kutta差分格式求出Y＊=,并且Y＊满足f＊=0(或者f为接近0的数)。那么解Y=(Y1,Y2,…,Yn)为所求初始状态变量的最优估计。

理想试验方法如下:首先在预先给定理想初始场Bm,借助正问题进行预报,获得T时刻的理想预报场;然后随机产生初始场B,通过预报获得T时刻的预报场(Y1,Y2,…,Yn);最后与理想个例的的误差来调整和优化初始场,进而得到最优的初始分析场Ba和T时刻相应的预报场

算法在MA TLAB7.1上实现,运行参数如下:子代规模μ=30、λ=200、pf=0.45,应用进化策略。作以下两组理想试验:(a)进化代数为4 000,10次独立试验,每次试验的初始场B不同;(b)最大进化代数分别设为1 000,2 000,3 000,4 000;在不同最大代数下,分别独立进行10次试验。为了更好地与理想个例比较,评价指标采用:

分析场与理想初始场间均方差

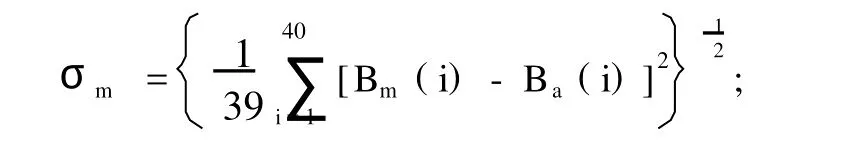
T时刻的分析预报场与理想预报场间均方差

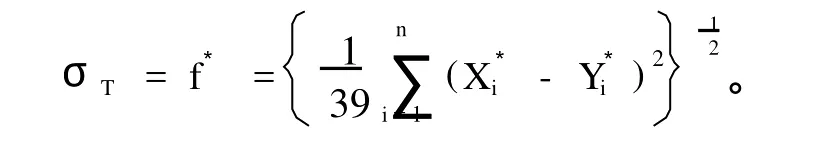
试验a的结果如表1所示。算法独立运行10次,每次的分析场B不同。从表1中优化结果可以看出,模式预报均方差已经较小,同时理想初始场Bm与分析场Ba的均方差也较小。即在不同的初始场下,算法的求解结果都非常理想,说明进化策略对初始场不敏感,算法的收敛性不受初始条件的取值范围影响。其次,分析场均方差均大于模式预报均方差,即在分析场均方差较大的情况下(分析场均方差均大于模式预报均方差),模式预报的均方差反而较小,从而验证了Lorenz-96模式具有非线性特征。

试验b中,所有试验的初始场B均相同,在不同进化代数下,算法运行10次得到的试验结果如表2所示。从表2中试验结果可以看出,在不同的进化代数下,经过优化,预报均方差的平均值、初始群体均方差的平均值都很小,再次说明此优化算法的有效性。另外,从预报均方差的方差、分析场均方差的方差均很小看出算法非常稳定;同时随着进化代数的增加,预报均方差的平均值及分析场均方差的平均值越小,即算法优化结果越好,即分析场Ba越接近理想初始场Bm。

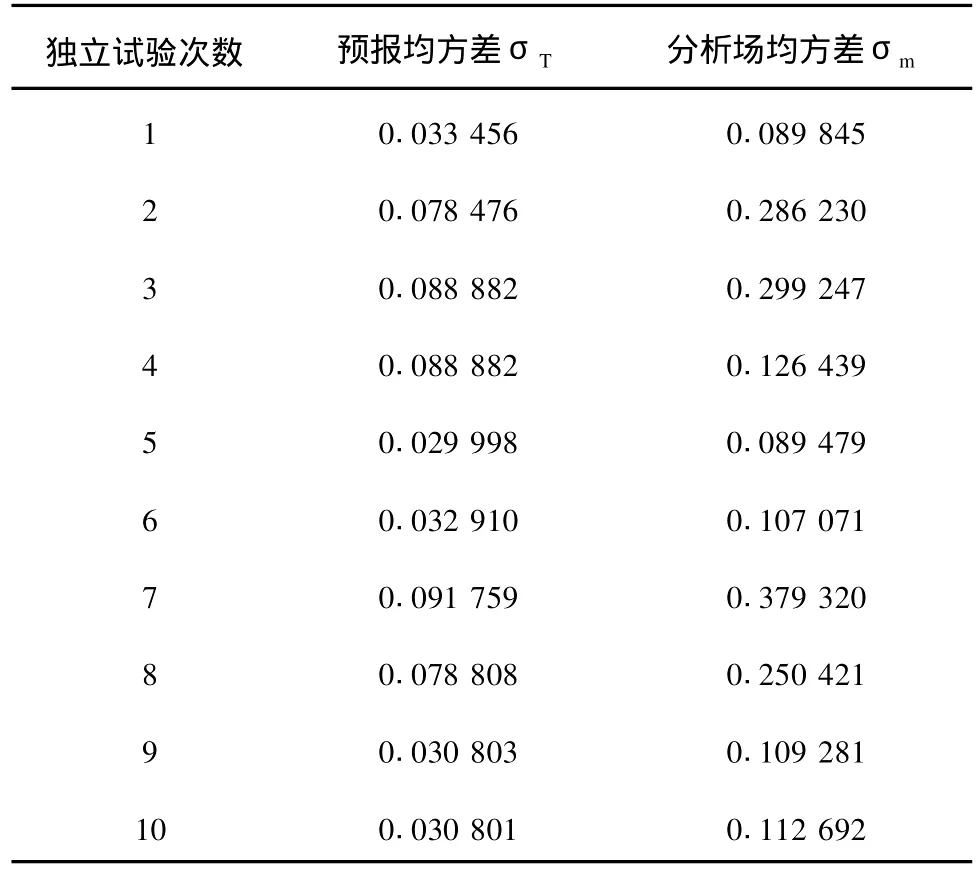
表1 试验a中的T时刻预报、分析场与理想个例间的均方差Table1 Mean square error of the forecast,analysis field and ideal case at time Tin experiment a

为了更好地展示预报误差调整初始场B的过程,以最大进化代数2 000中的某次试验为例,给出进化代数和预报误差的关系,如图3所示。随着进化代数的增加,预报误差f＊的总体趋势逐渐减小,虽然在某些代数上存在较小的波动,但这符合进化策略采用的选择策略特性。在算法结束时,预报误差f＊已经调整的较小,即进化策略反演出Lorenz-96模式的初始状态与实际的初始状态很接近,表明应用进化策略求解Lorenz-96模式的初始场反问题是可行的。但没法使得预报误差f＊为0,这恰恰也说明Lorenz-96模式存在很强的非线性。

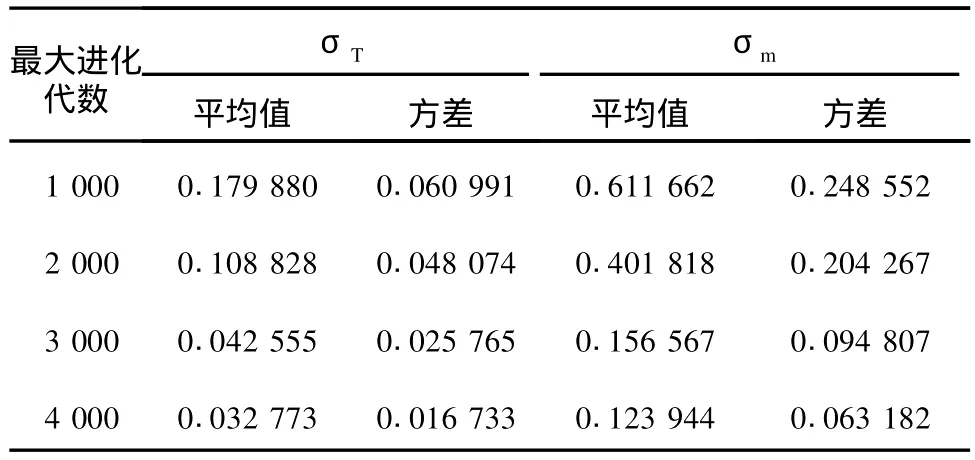
表2 不同进化代数下的T时刻预报、分析场与理想个例间的均方差Table2 Mean square error of forecast,analysis field and ideal case at time Tin different evolution generations

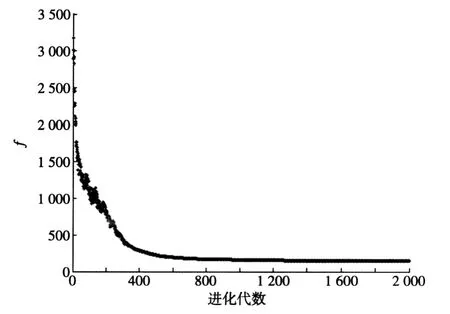
图3 预报误差f与进化代数之间的关系Fig.3 Relationship be tween forecast errorf and evolution generations

4 结论与讨论

在研究气象学上的天气数值预报时,提出了一种基于进化策略的气象学反问题求解算法,并借助预报模式中的参数识别和初始场反问题,通过问题转化变成等价函数优化问题,进而采用进化策略求解。为验证方法的有效性,通过一维扩散方程和Lorenz-96预报模式中的反问题进行理想数值试验,实验结果表明应用进化策略求解预报模式中的参数识别问题和初始场反问题是可行的,算法都能求解到理想的结果。但对于初始场中的变量协调问题,可转化为带约束优化问题,是下一步的研究方向。

当然,依据现有的计算机发展水平,暂且无法将进化策略直接用于当前业务预报模式中(如W RF、MM5等)。主要是因为:一是进化算法的优化精髓是“生成—测试”方法,即需进行频繁评估;二是由于业务模式非常复杂,在其上进行一次评估是非常耗时的,即无法满足业务对时间的要求。我们也坚信随着计算机硬件和并行算法的不断发展,在不远的将来进化算法也将为推动气象研究与发展作出努力。

[1] 任宏利,丑纪范.数值模式的预报策略和方法研究进展[J].地球科学进展,2007,22(4):376-385.

[2] Kalnay E.A tmospheric modeling,data assim ilation and predictability[M].Cambridge:Cambridge University Press,2003.

[3] 郜吉东,丑纪范.数值天气预报中两类反问题及一种数值解法[J].气象学报,1994,52(2):129-137.

[4] 邱崇践,丑纪范.预报模式的参数优化方法[J].中国科学,1990,2(2):218-224.

[5] 吴志健.演化优化及其在微分方程反问题的应用[D].武汉:武汉大学计算机学院,2004.

[6] Coello C A C.Twenty years of evolutionary multi-objective optimization:A historical view of the field[J].IEEE Computational Intelligence Magazine,2006,1(1):28-36.

[7] Thomas P R,Xin Yao.Search biases in constrained evolutionary optimization[J].IEEE Transactions on Systems,2005,5(2):233-243.

[8] 常新功,李敏强,寇纪淞.基于进化算法的图形数据模式发现[J].模式识别与人工智能,2008,21(1):116-121.

[9] 马清亮,胡昌华.多目标进化算法及其在控制领域中的应用综述[J].控制与决策,2006,21(5):481-486.

[10] 李守巨,刘迎曦,孙伟.智能计算与参数反演[M].北京:科学出版社,2008.

[11] 韩静.利用星载超光谱仪器观测资料进行大气参数反演的试验[D].南京:南京信息工程大学遥感学院,2008.

[12] 王文强.基于Lorenz-96模式的集合平方根滤波同化方法研究[D].兰州:兰州大学大气科学学院,2007.

[13] 熊盛武,李元香,康立山,等.抛物型方程的演化参数识别方法[J].计算物理,2000,17(5):511-517.