基于灵敏度分析的改进遗传算法
李建福,陈义保
(烟台大学 机电汽车工程学院,山东烟台 264005)
遗传算法是上个世纪70年代由美国密执安大学的Holland教授提出的[1],是一种基于自然遗传和自然选择机理的全局寻优搜索方法。因为具有简单通用、鲁棒性强、适于并行处理以及高效、实用等显著特点,所以其在各个领域得到了广泛应用,取得了良好效果,并逐渐成为重要的智能算法之一。但在实际应用过程中,遗传算法也暴露出了一些自身所固有的缺点,比如容易早熟、局部寻优能力差、求解精度不高等。
传统的遗传算法,可以很快到达最优解的90%左右[2],但是要达到最优解,往往还需要大量的时间,也就是遗传算法具有较强的全局搜索能力,但是其局部搜索能力不强。本文提出的基于灵敏度分析的改进遗传算法,将目标函数提供的导数信息加入到算法的搜索过程中去[3],使种群中的优秀个体,能按照指定的方向继续进化,有效地提高了算法的局部搜索能力。同时,在该算法中融入了小生境技术,其应用有效地保持了种群的多样性,提高了全局搜索能力,避免陷入局部最优解。
1 算法策略
1.1 小生境算法
小生境是指在特定环境中一种组织的功能,而把有共同特性的组织称为物种。该技术就是将每一代遗传个体分成若干类,从每个类中选出若干适应度较大的个体,作为一个类的优秀代表组成一个种群,再在种群中以及不同的种群之间通过杂交、变异,产生新一代个体群。本文使用的是基于排挤的小生境算法[4],其基本思想是依据个体之间的相似性,将种群分为若干个小生境,并排挤掉同一小生境中的较差的个体。这样,各小生境中的最优个体,便可以认为是局部最优解邻域内的一点。个体之间的相似性,用编码串之间的海明距离来度量:
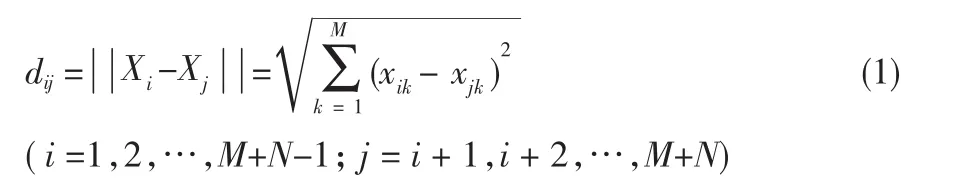
很显然,dij越小,Xi和 Xj的相似程度就越大;dij越大,Xi和Xj的相似程度就越小。如果dij<L (L为设定的一较小的正数),也就说明它们属于同一小生境,那么就对适应度较小的施加较强的惩罚函数Fmin=Penalty,其中Penalty为一个很小的正数。在基本遗传算法运行的后期,小生境技术的融入,能克服适应度高的个体大量繁殖而充满整个群体的缺陷,避免早熟现象的发生,保证了种群的多样性及对整个解空间的搜索。
1.2 敏度分析原理
灵敏度就是导数信息,从数学意义上讲,它反映了函数对某些自变量xi的变化梯度,若函数F(x)可导,其一阶灵敏度S在连续系统中,可表示为S=F(x)/xi;在离散系统中,可表示为S=ΔF(x)/Δxi,分别为一阶微分灵敏度和一阶差分灵敏度[5]。当前灵敏度计算方法主要有3类:解析法、差分法和两者混合的半解析法。解析法精度有保证,差分法和半解析法求解过程简单,易于工程实现。
在遗传算法中引入目标函数的导数信息,就可以通过灵敏度向量所指的方向寻找最优解,如果设问题的目标函数为f(x),种群中个体维数为m,那么目标函数f(x)的m维灵敏度向量可以表示为:

如果该向量方向始终指向增长方向,说明该方向是指向最大值,那么朝相反的方向移动则得到极小值,即:

如果该向量方向指向下降的方向,说明该方向是指向最小值,那么沿着该方向移动便得到最小值:

其中,η称为步长,是一个很小的正数。
在实际应用中,由于某些目标函数不具有可导性,有些甚至无法写出数学表达式,因此目标函数的导数信息往往不能用解析式表达出来。为了简便起见,本文将利用目标函数的一阶偏微分,来近似地代替其导数信息,即表示为:

对群体中每个小生境的最优个体进行基于灵敏度向量的局部寻优,就能使个体向局部最优解不断地靠近,从而增强了算法的局部搜索能力,提高了算法的计算精确度,具体步骤如下:

else个体X已经到达了峰值。
2 遗传算子
2.1 选择算子
轮盘赌选择法是一种回放式随机采样方法,也是遗传算法中最早被提出来的一种方法。因为这种方法简单而且实用,所以被广泛使用。但由于随机操作的原因,这种选择方法的选择误差比较大,有的时侯甚至会出现“退化”现象,这样便使适应度较高的个体失去了选择机会。因此本文选用了一种改进的多轮轮盘选择算子[6],改进的选择算子每产生M个随机数来确定一个个体,取代了传统轮盘赌算子中的每产生一个随机数确定一个个体,这样产生随机数的数量由原来的M增至M2,使随机数的作用体现的更精确,从而降低了随机操作所产生的误差,提高了算子的选优能力,确保了优秀的个体能够存留下来。
2.2 交叉算子
交叉运算是产生新个体的主要方法,它决定了遗传算法的全局搜索能力。为了提高算法的全局搜索能力,本文采用算术交叉算子[7]。交叉后一点落于进行交叉的父代之间,另一点落于靠近较好父代的一侧,使解能朝着较好的方向发展。自适应交叉系数,能使交叉量随着进化代数的增大而减小。在算法中随机选取两个交叉个体Xi和Xj,先比较这两个个体的适应度值F(Xi)和F(Xj),在这里我们可以假设F(Xi)>F(Xj),交叉点选为xik和xjk,那么交叉结果可以表示为:

其中

a0为预定系数;
t为当前进化代数;
T为最大进化代数;
Nk为取值范围的上限;
Mk为xik取值范围的下限。
2.3 变异算子
变异运算虽是产生新个体的辅助方法,但也是必不可少的一个步骤,决定了遗传算法的局部搜索能力。为了增强算法的局部寻优能力,本文引入非均匀变异算子,重点搜索原个体附近的微小区域。如果变异个体设为X,变异点设为xi,取值范围为[Nk,Mk],那么变异结果由下式决定:
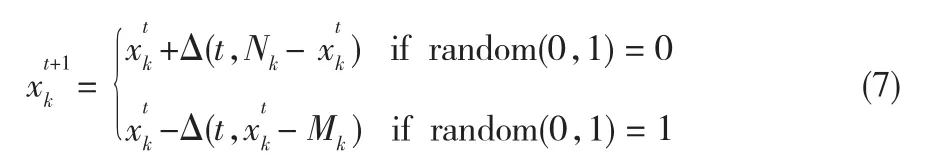
式中
△(t,y)=y·(1-r(1-t/T)b),△(t,y)表示[0,y]范围内符合非均匀变异的一个随机数;
r为[0,1]范围内的符合均匀分布的一个随机数;
T为最大进化代数;
b为一个系统参数。
由此可见,该算法在进化的初始阶段,将近似地进行均匀随即搜索,随着进化的延续,到了后期该算法将重点搜寻个体附近的微小区域,也就是进行局部搜索。
3 算法流程
算法的具体步骤如下:
Step1:设置进化代数,随机产生M个初始个体组成初始种群 p(t),并求出各个个体的适应度 Fi(i=1,2,…,M)。
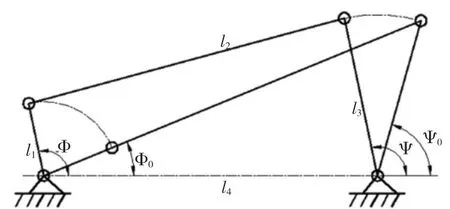
Step2:根据个体的适应度对其进行降序排列,记忆前N个个体(N Step3:选择运算。用前面提的多轮轮盘赌法,对群体P(t)进行选择运算,得到种群p'(t)。 Step4:交叉运算。对种群p'(t)进行算术交叉运算,得到种群p''(t)。 Step5:变异算法。对种群p''(t)进行非均匀变异运算,得到种群p'''(t)。 Step6:小生境排挤运算。将上面经过选择、交叉、变异运算得到的M个个体和步骤2所记忆的N个个体合并在一起,得到一个含有M+N个个体的新群体。按照式(1)求出这M+N个个体中每两个个体Xi和Xj之间的海明距离。当 Xi-Xj莨L时,比较个体Xi和Xj的适应度大小,并对其中适应度较低的个体处以罚函数。 Step7:敏度优化运算。按照式(5)计算得到的灵敏度向量,对这M+N个个体进行灵敏度优化。 Step8:计算、评价这M+N个个体,按适应度降序排序,并分别记录记忆前M和前N个个体。 Step9:终止条件判断。若不满足终止条件,则:t=t+1,并将步骤8排序中的前M个个体作为新的下一代群体P(t),转到步骤3;若满足终止条件,则输出计算结果,算法结束。 为了验证本文提出的改进算法的性能,选用Shubert作为测试函数,这是一个多峰函数,该函数在其定义域内共有760个局部最小值,其中18个是全局最小值。全局最优点处的函数值为F=-186.73090883,其函数数学表达式如下: 本试验用Matlab语编写程序,种群规模M=100,记录优秀个体为N=40,最大进化代数T=500,交叉概率pc=0.8,变异概率pm=0.1,海明距离下限L=0.4,罚函数Penalty=10-3,自适应交叉参数a0=40.0,灵敏度运算中参数η=10-4。 表1给出了本文算法与常规遗传算法(GA)、基本小生境遗传算法(NGA)、改进的小生境遗传算法(GNGA)[8]的性能对比: 表1 本文算法与其他遗传算法的性能对比 从表1中的结果可以明显看出,本文所使用的改进算法对多峰Shubert函数进行全局寻优,收敛速度明显比其他遗传算法要快,计算结果的精确度也较高。 以文献[9]中的曲柄摇杆机构再现运动规律为优化实例。所谓再现运动规律,是指当主动件运动规律一定时,要求从动件按给定规律运动[10],曲柄摇杆机构简图如下所示: 图1 曲柄摇杆机构简图 由于按比例对杆件的长度进行缩放,将不会改变曲柄摇杆机构的运动规律,所以通常情况下设l1=1,l2、l3可由l1决定,机架长l4事先给定,因而设计变量定为: 其中l2、l3为杆件尺寸。 以给定的运动规律与机构实际运动规律间的偏差最小为目标函数,即: 其中ΨEi为期望输出角,Ψi为实际输出角,m为输入角的等分数。 约束条件由传动角满足的许用值和曲柄摇杆机构满足的曲柄存在条件决定,传动角的最大最小许用值为,通过计算整理得约束为: 用基于灵敏度分析改进的遗传算法,对曲柄摇杆机构再现运动规律进行优化,并与小生境GA[9]及罚函数法[10]的优化结果进行对比,如表2所示。 表2 本文算法与其他算法的计算结果对比 如表2所示,本文的算法收敛精度较高,而且结果更优。 本文将传统优化算法的精髓导数信息引到了遗传算法中,在保证了算法的全局搜索能力的同时,加强了算法的局部搜索能力。小生境技术的利用,增加了种群中个体的多样性,在保留了最优解的同时,有效的防止了早熟现象的发生。改进的遗传算子,改善了算法的各项性能,有效提高了算法的可靠性。通过对多峰Shubert函数的仿真试验,说明该算法能有效的提高局部搜索能力及解的精度;对曲柄摇杆机构再现运动规律的实例优化,表明该算法具有一定实际应用价值。 [1]Holland J H.Adaptation in Natural and Artificial Systems[M].Cambridge,MA,USA:MIT Press,1975. [2]周洪伟,徐松林,徐 静.改进的小生境遗传算法[J].软件时空,2007,23(6-3):208-209. [3]何新贵,梁久祯.利用目标函数梯度的遗传算法[J].软件学报,2001,12(7):981-986. [4]周 丽,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,2001. [5]HAFTKA R T.Second order sensitivity derivatives in structural optimization[J].AIAA Journal,1982,(20):1765-1766. [6]陈友文.一种改进选择算子和基于小生境的遗传算法[J].计算机与数字工程,2006,37(6):21-24. [7]董 颖,刘欢杰.一种基于实数编码的改进遗传算法[J].东北大学学报,2005,26(4):119-221. [8]黄聪明,陈湘秀.小生境遗传算法的改进[J].北京理工大学学报,2004,24(8):675-678. [9]陈格娟,崔 炜,张京军.小生境遗传算法在机械优化设计中的应用[J].河北建筑科技学院学报,2004,21(1):56-59. [10]刘惟信.机械最优化设计[M].北京:清华大学出版社,1994.4 试验及实例优化
4.1 试验及分析
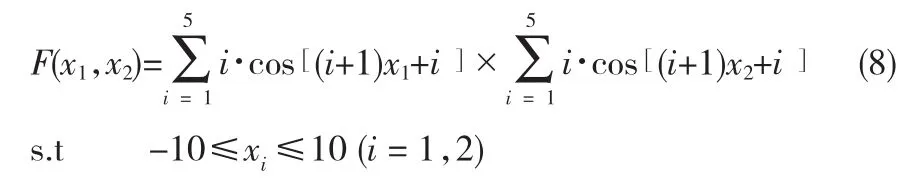

4.2 实例优化



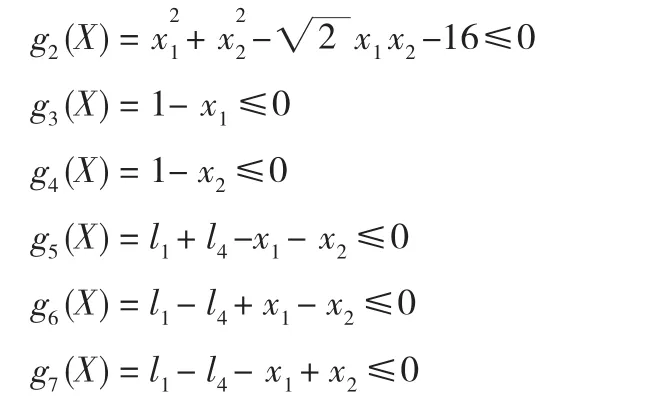

5 结束语
——以贵阳花溪公园为例

