非正态参数二维分叉裂纹扩展寿命的可靠性分析

张艳林 张义民 金雅娟 张艳芳

1.东北大学，沈阳，110004 2.防灾科技学院，三河，065201

0 引言

由于绝大多数工程结构的破坏形式是疲劳破坏，且破坏多由疲劳裂纹的扩展所致，因此研究结构疲劳破坏问题是很有意义的课题［1－4］。在实际构件中，往往由于过载、裂纹尖端塑性区尺寸大小、裂纹尖端材料的微观属性等因素导致裂纹的分叉，而发生分叉后的裂纹扩展行为与单一裂纹的扩展行为是不同的，新产生的裂纹虽然很微小但对于原始主裂纹的扩展有很大的影响，主要表现为对原始主裂纹扩展方向及扩展速率的影响，裂纹的分叉对主裂纹的扩展起到抑制作用，进而延长了裂纹扩展寿命［5］，因此研究分叉裂纹的扩展寿命可靠性问题具有重要的工程意义。

分叉裂纹扩展研究通常是建立在确定性分析基础上的，由于结构尺寸、材料属性、载荷等因素具有不可避免的随机性，疲劳裂纹扩展过程是一个随机过程，因此建立在统计理论基础上的裂纹扩展寿命可靠性分析要比传统确定性模拟给出的结果更加符合工程实际。在工程实际中，由于统计数据的缺乏，使得一些随机变量的具体分布形式未知，而仅仅知道它们的前几阶矩。在这种情况下，可以采用四阶矩可靠性分析方法进行近似的可靠性分析。

本文在随机有限元法基础上，结合计算可靠度的四阶矩法及二维分叉裂纹扩展分析方法、应力强度因子数值计算方法，提出参数服从非正态分布时二维分叉裂纹扩展寿命可靠度的分析方法。

1 摄动随机有限元法

线性有限元方程为

式中，K为整体刚度矩阵；U为节点位移向量；P为节点力向量。

式中，下标d表示随机变量（向量）的均值。

将式（3）代入式（1）中并展开，比较ε的同次幂系数，略去高次幂系数，经过化简后可得方程：

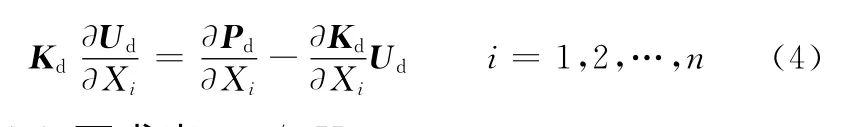
由式（4）可求出∂U／∂Xi。

进一步可求得位移U的均值、方差（协方差）、三阶矩、四阶矩：

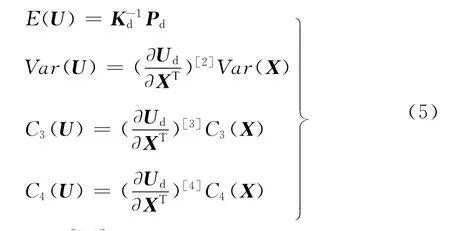
式中，（·）［k］＝ （·）［k－1］⊗ （·）＝ （·）⊗ （·）⊗ … ⊗ （·），为（·）的Kronecker幂，符号⊗表示Kronecker积，定义为（A）p×q⊗（B）s×t＝［aijB］ps×qt；Var（X）、C3（X）、C4（X）分别为基本随机参数X的方差（协方差）、三阶矩、四阶矩矢量。

2 四阶矩可靠性设计

结构可靠度是计算联合概率密度函数fx（X）在区域g（X）＞0内的多维积分：

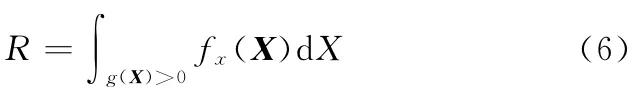
其中，g（X）为状态函数，可表示零件的两种状态：

4.水质管理 进入6月后，逐渐将水位提高至1m。定期使用二氧化氯对水体进行消毒，两天后使用解毒活水宝改良水质。隔一天后使用生物肥，用量为4kg/亩，至体长5cm以后停止使用。每10～15天用生石灰化浆泼洒一次，提高水体钙含量，促进蜕壳，用量为每亩每米水深5kg。养殖期间适时开启增氧机，保证水体溶氧丰富。每15～20天左右使用微生物制剂一次。整个养殖期间保持水质清新，透明度保持在40～50cm。

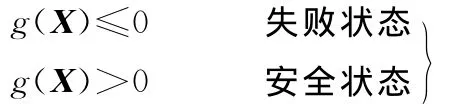
设状态函数g的前四阶矩分别为：均值μg、σg、α3g、α4g。

四阶矩可靠性指标定义为［7］

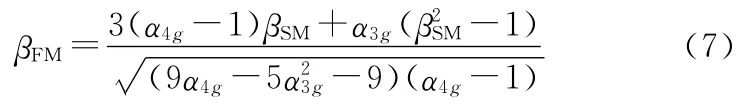
式中，βSM为二阶矩可靠性指标，定义为βSM＝μg／σg。

失效概率为

式中，Φ为标准正态分布函数。

采用四阶矩可靠性分析，可以避免对基本变量分布类型的依赖，与一次二阶矩可靠性分析相比，可以求出更加精确的解。裂纹扩展问题中，结构材料常数、裂纹扩展率常数、应力强度因子等参数往往无法知道其分布类型，但对于其前几阶矩统计特性有时可以通过少量样本获得，因此可以采用四阶矩法进行可靠性近似分析。

3 应力强度因子求解

在裂纹尖端处采用具有1／4节点的奇异单元，其他部分采用8节点常规等参元进行网格划分，图1显示了裂纹尖端奇异单元及裂尖处局部坐标。

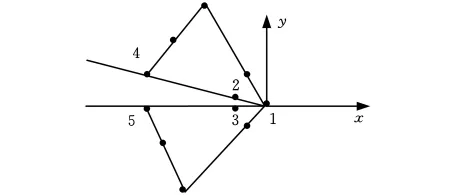
图1 裂纹尖端奇异单元及局部坐标

应力强度因子可采用式（9）、式（10）计算［8］：

式中，KⅠ、KⅡ分别为Ⅰ型、Ⅱ型应力强度因子。

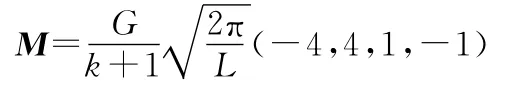
其中，当应力状态为平面应力时，k＝（3－μ）／（1＋μ）；当应力状态为平面应变时，k＝3－4μ；G为材料的剪切模量；μ为材料的泊松比；L为裂尖处奇异单元的长度；ui、vi分别为节点i沿x方向、y方向的位移。

由于结构的材料特性、载荷都是随机变量，因此位移也是随机量，因此等效应力强度因子Keq也是随机变量，其前四阶矩统计特性为

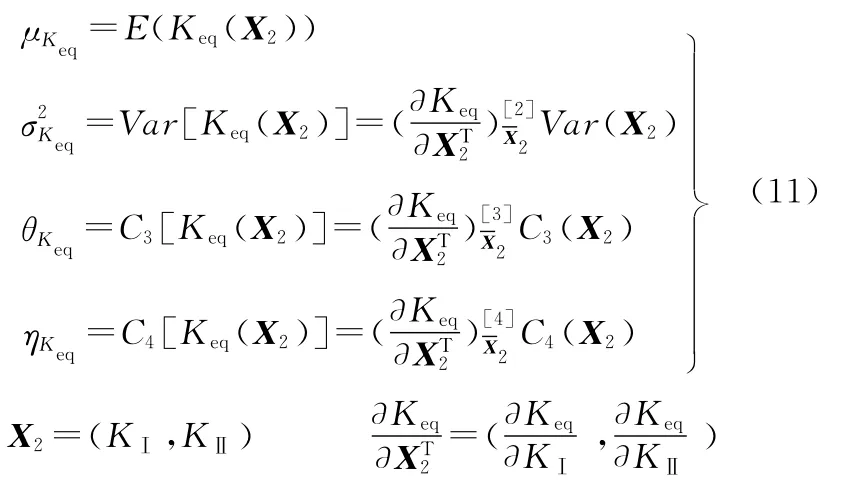
由最大周向应力理论确定裂纹扩展角，等效应力强度因子 Keq为［9］

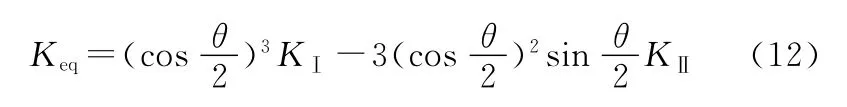
裂纹扩展角θ为

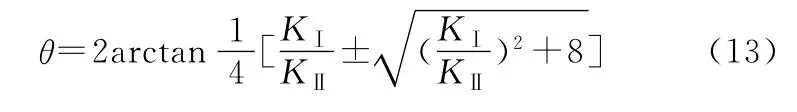
4 扩展寿命的可靠性分析

采用修正的Paris－Erdogan公式［10］，计算分叉裂纹扩展寿命：

式中，a0、ac分别为裂纹初始长度和裂纹最终长度；C、m为裂纹扩展率常数；ΔKth为应力强度因子变化范围门槛值；ΔKeq为等效应力强度因子变化范围分别为裂纹扩展段中的最大和最小等效应力强度因子。

将裂纹扩展过程离散成s个裂纹扩展段，则式（14）可写成如下的分段形式：

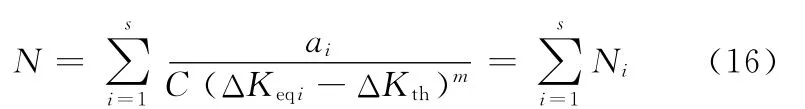
式中，ai为第i段裂纹扩展长度；ΔKeqi、Ni分别为与ai相对应的等效应力强度因子变化范围和裂纹扩展寿命。

长短裂纹对应的扩展长度为

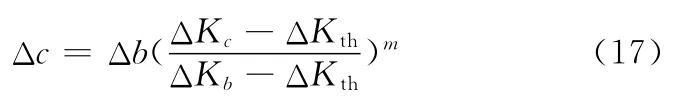
式中，Δc、Δb、ΔKc、ΔKb分别为每个扩展段长短裂纹对应的扩展长度及其对应的应力强度因子变化范围。

疲劳扩展寿命可靠性分析的功能函数为

式中，Nc为结构的设计寿命。

裂纹总的扩展寿命等于每段扩展寿命之和：

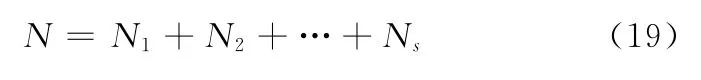
要使用第2节中方法进行裂纹扩展寿命可靠性分析，需要已知g的前四阶矩统计特性。首先要求出Ni（i＝1，2，…s）的前四阶矩，由式（19）可知，Ni是ai、C、m、ΔKeqi的函数，其前四阶矩为

疲劳裂纹扩展寿命可靠度的具体计算步骤如下：①采用随机有限元法，由式（4）计算位移对基本随机参数（载荷、材料特性）的偏导数，通过式（5）算出位移的前四阶矩；② 通过式（11）计算应力强度因子Keq的前四阶矩统计特性；③应用式（20）计算Ni的前四阶矩，进而求出功能函数g的前四阶矩；④采用第2节所述的四阶矩可靠性设计方法计算疲劳裂纹扩展寿命可靠度。

5 数值算例

如图2所示有一长方形板，板的一侧有已发生分叉的斜裂纹，两裂纹的夹角为90°，板的上下两边受均布力作用，板的各个参数及其统计特性（均值、方差、三阶矩、四阶矩）如下［10-11］：长度L＝80mm，宽度b＝30mm，泊松比μ＝0.3；初始斜 裂 纹 长 度a0＝（3 ±0.05）mm，最 终 裂 纹 长 度ac＝（8±0.05）mm，弹性模量E的统计特性（均值、方差、三阶矩、四阶矩）为（205 000，2050，2.6 × 108，5.3×1013）MPa，载荷σmax的统计特性（均值、方差、 三 阶 矩、 四 阶 矩 ） 为 （60，1.8，0.525，31.6441）MPa，σmin的统计特性（均值、方差、三阶矩、四阶矩）为（30，0.9，0.0656，1.9778）MPa，裂纹扩展率参数C的统计特性（均值、方差、三阶矩、四阶矩）为（9×10－11，0.45×10－11），m的统计特性（均值、方差、三阶矩、四阶矩）为（2.2，0.11，2×10－4，4.5×10－4），应力强度因子门槛值Kth的统计特性（均值、方差、三阶矩、四阶矩）为（35，0.7，0.0206，0.7218）

图2 两边受拉伸的分叉斜裂纹板

图3为裂纹尖端网格的划分图。图4为裂纹扩展寿命随裂纹扩展长度的变化规律图，图5为裂纹扩展寿命可靠度随设计寿命变化的曲线图。

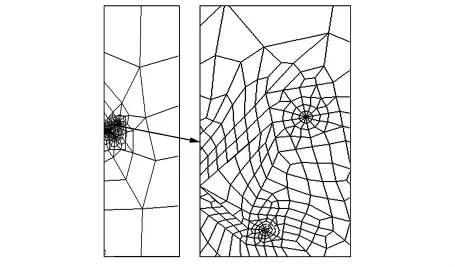
图3 整体网格图与裂纹处网格放大图

图4 疲劳寿命随裂纹扩展长度的变化趋势

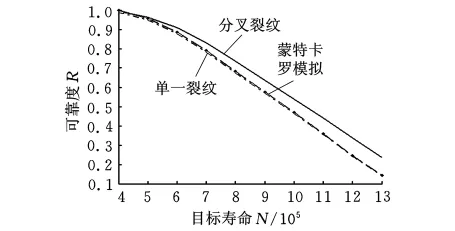
图5 可靠度随设计寿命的变化趋势

6 结论

基于随机有限元法、四阶矩可靠性分析方法、分叉裂纹扩展方法、应力强度因子数值算法，提出了随机参数服从任意分布时的二维分叉裂纹扩展寿命的可靠性分析方法。从结果可以看出，随着裂纹的扩展，裂纹板的剩余强度（剩余寿命）逐渐减小，寿命可靠度不断降低。对分叉主裂纹及无分叉单一主裂纹扩展行为进行对比，当裂纹扩展长度相同时，发生分叉的裂纹扩展寿命要比原始裂纹的扩展寿命长，说明分叉裂纹对主裂纹扩展有限制作用，与相关文献得出的结论一致。新方法对具有二维分叉裂纹工程板结构的疲劳破坏的评定、设备的检修有一定指导意义。

［1］ Yates J R，Zanganeh M，Tomlinson R A，et al.Crack Paths under Mixed Mode Loading［J］.Engineer Fracture Mechanics，2008，75（3／4）：319－330.

［2］ Pavou D G，Labeas G N，Vlachakis N V，et al.Fatigue Crack Propagation Trajectories under Mixedmode Cyclic Loading［J］.Engineering Structures，2003，25（7）：869－875.

［3］ Peng X Q，Liu Geng，Wu Liyan，et al.A Stochastic Finite Element Method of Fatigue Reliability Analysisof Gear Teeth Subjected to Bending［J］.Computational Mechanics，1998，21（3）：253－261.

［4］ 张艳林，张义民，金雅娟.任意分布参数疲劳裂纹扩展寿命的可靠性分析［J］.应用力学学报，2009，26（3）：604－607.

［5］ Meggiolaro M A，Miranda A C O，Castro J T P，et al.Stress Intensity Factor Equations for Branched Crack Growth［J］.Engineering Fracture Mechanics，2005，72：2674－2671.

［6］ 张义民.汽车零部件可靠性设计［M］.北京：北京理工大学出版社，2000.

［7］ Zhao Y G，Ono T.Moment Method for Structural Reliability［J］.Structural Safety，2001，23：47－75.

［8］ Barsoum R S.Triangular Quarter－point Elements as Elastic and Perfectly－plastic Crack Tip Elements［J］.Engineering Fracture Mechanics，1977，11：85－98.

［9］ 高庆.工程断裂力学［M］.重庆：重庆大学出版社，1986.

［10］ Meggiolaro M A，Miranda A C O，Castro J T P，et al.Crack Retardation Equations for the Propagation of Branched Fatigue Cracks［J］.International Journal of Fatigue，2005，27：1398－1407.

［11］ 中国航空研究院.应力强度因子手册［M］.北京：科学工业出版社，1993.