简述不等式恒成立问题的几种求解策略
●曹江谊 (苏溪中学 浙江义乌 322000)
不等式恒成立问题是高中数学中的一类典型问题,也是历年高考的热点题型之一.确定不等式恒成立中参数的取值范围,需灵活应用函数与不等式的基础知识,并时常要在两者间进行合理的交汇,因此此类问题属于学习的重点.怎样确定其取值范围呢?课本中却从未论及,但它已成为近年来命题测试中的常见题型,因此此类问题又属学习的热点.在确定恒成立不等式中参数的取值范围时,需要在函数思想的指引下,灵活地进行代数变形、综合地运用多科知识,方可取得较好的效益,因此此类问题的求解是学习的难点.基于此,本文试对此类问题的求解策略与方法作一提炼总结.
1 最值法
是将不等式恒成立问题转化为求函数最值问题的一种处理方法,其一般类型有:
(1)f(x)>a恒成立⇔a<f(x)min;
(2)f(x)<a恒成立⇔a>f(x)max.

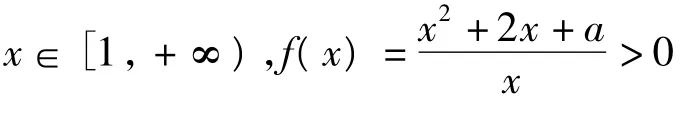
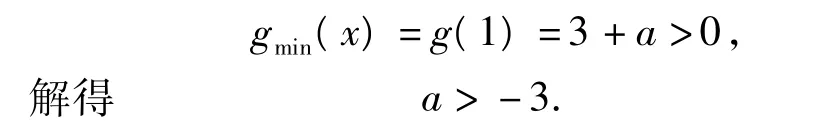
2 分离变量法
若所给的不等式能通过恒等变形使参数与主元分离于不等式的2端,从而使问题转化为求主元函数的最值,进而求出参数的取值范围.这种方法的本质也还是求最值,但它的思路更清晰、操作性更强.一般有:
(1)f(x)<g(a)(a为参数)恒成立⇔g(a)>f(x)max;
(2)f(x)>g(a)(a为参数)恒成立⇔g(a)<f(x)max.
实际上,例1就可利用此法解决.
略解 x2+2x+a>0在x∈[1,+∞)时恒成立,只要a>-x2-2x在x∈[1,+∞)时恒成立.易求得二次函数h(x)=-x2-2x在[1,+∞)上的最大值为-3,因此a>-3.

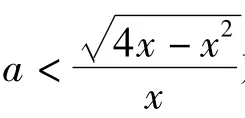
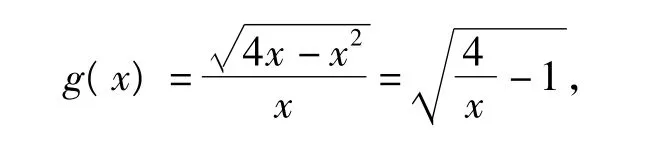
可知g(x)在(0,4]上为减函数,因此

得a<0,即a的取值范围为(-∞,0).
评注分离参数后,方向明确、思路清晰,能使问题顺利得以解决.
3 变换主元法
将原先不等式的主元变换成另外一个主元,以变换后的主元为自变量构造函数,利用构造出的函数图像与性质进行求解.
例3 对任意 a∈[-1,1],不等式 x2+(a-4)x+4-2a>0恒成立,求x的取值范围.
分析题目中的不等式是关于x的一元二次不等式,但若把a看成主元,则问题可转化为一次不等式(x-2)a+x2-4x+4>0在 a∈[-1,1]上恒成立的问题.
解令f(x)=(x-2)a+x2-4x+4,则原问题转化为f(a)>0在a∈[-1,1]上恒成立.
当x=2时,可得f(a)=0,不合题意;
当x≠2时,应有
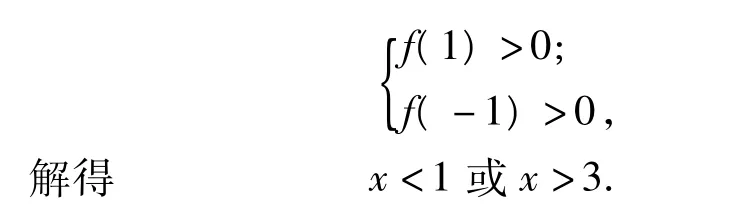
故x的取值范围为(-∞,-1)∪(3,+∞).
评注变换主元法其实是一种“反客为主”的策略:把欲求字母变量作为“客”即参数,题设中有范围的字母变量作为“主”即自变量.
4 求导法
当不等式中出现3次以上的多项式函数、指数函数、对数函数等函数时,可考虑利用导数知识探求问题的解法.
例4 已知函数
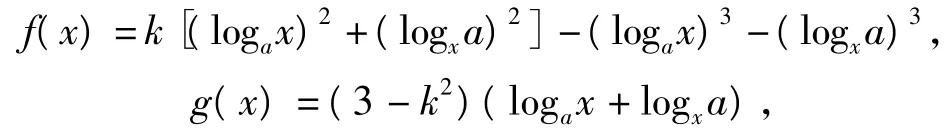
其中a>1,试问当k取何值时,不等式f(x)<g(x)对任意的x∈(1,+∞)恒成立?
分析注意到logax与logxa是倒数关系,设t=logax+logxa,可对函数f(x),g(x)的表达式进行化简,进而将题设不等式转化关于t的不等式,利用导数求解.
解设t=logax+logxa,则
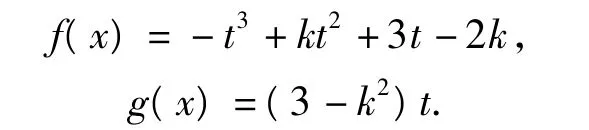
由x∈(1,+∞)且 a>1,可得 t≥2,因此不等式f(x)<g(x)对任意的x∈(1,+∞)恒成立,等价于t3-kt2-k2t+2k>0对任意t≥2恒成立.设h(t)=t3-kt2-k2t+2k,则函数 h(t)在[2,+∞)上的最小值大于0,于是

由导数知识得
当 k≥2时,h(x)min=h(k)>0,解得 k∈φ;
当0<k<2时,k(x)min=h(2)>0,解得

当 k=0时,h'(t)=3t2>0,即 h(t)在[2,+∞)上是增函数,于是

当 -6≤k<0时,h(x)min=h(2)>0,解得
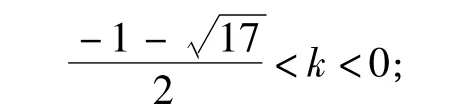
评注利用导数研究函数单调性、极值点情况,进而描绘出函数的大致图像,是解决此类问题的关键.若情况复杂,则还需进行分类讨论.
5 构建函数法
当参数难以分离而不等式是有关某个变量的一次或二次函数时,可以通过构建函数来解决.我们知道,函数概念是高中数学的一个很重要的概念,其思想和方法已渗透到数学的各个分支.在某些数学问题中,通过数式类比,构造适当的函数模型,然后利用函数的有关性质结论解题,往往能收到意想不到的效果.这里,主要介绍如何通过构造一次函数、二次函数模型,并利用它们的性质来确定参数的取值范围.
5.1 构造一次函数
例5 若对一切|p|≤2,不等式(log2x)2+plog2x+1>2log2x+p恒成立,求实数x的取值范围.
解原不等式可变形为
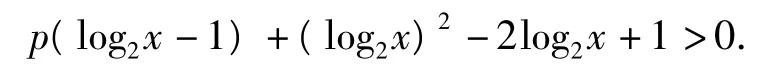
现在考虑p的一次函数:
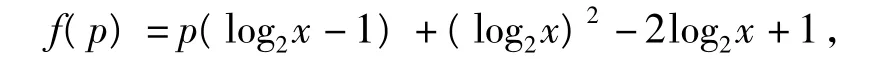

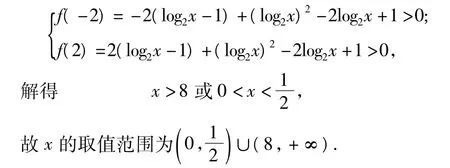
解原不等式可变形为
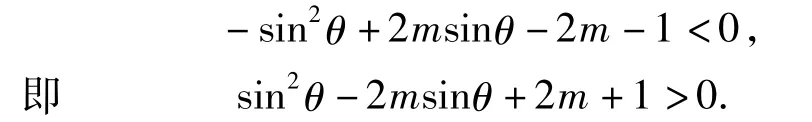
令 sinθ=t,t∈[0,1],则
评注本题对于一切|p|≤2,原不等式恒成立,因此应视p为主元,视x为参数,把不等式变成关于p的一次函数型.
5.2 构造二次函数
例6 对于

令f(t)=t2-2mt+2m+1,因此可转化为f(t)>0在 t∈[0,1]上恒成立,从而

评注二次函数图像由其开口方向、顶点和对称轴这三要素确定.当对称轴中含有字母参量时,要先讨论其与给定区间的位置关系,然后才能确定函数在给定区间上的最值.
6 基本不等式法
当不等式中涉及的字母变量较多而无法将不等式恒成立问题转化为函数问题时,应考虑使用基本不等式求解.

分析由条件推出函数f(x)的单调性.据单调性“脱”去不等式中的“f”得到关于 x,y,a的普通不等式,利用基本不等式求a的取值范围.
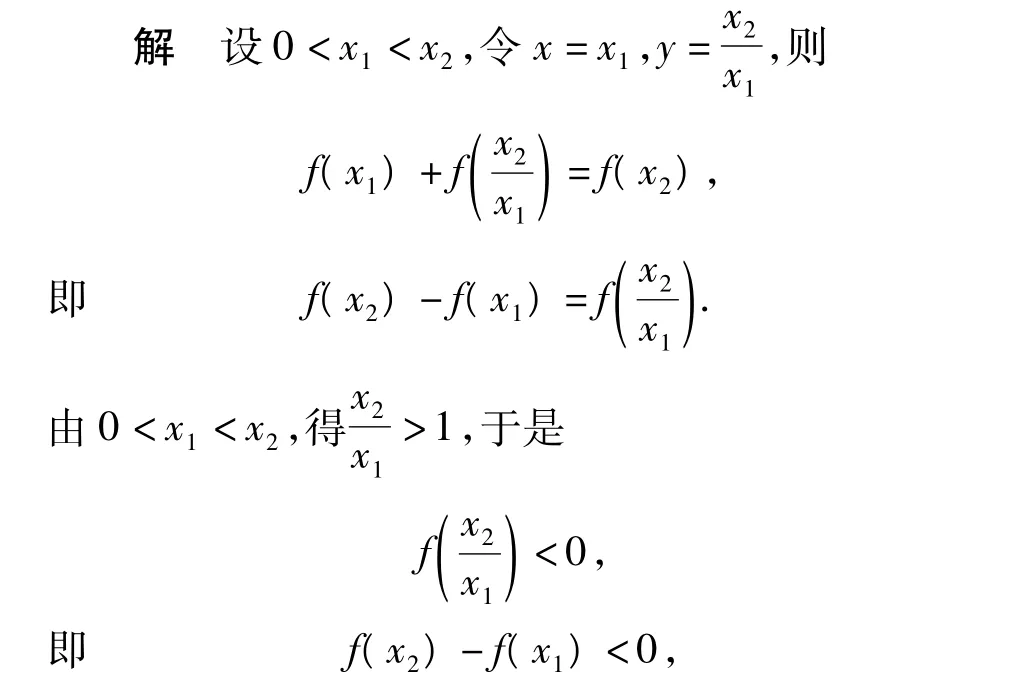
得f(x)在(0,+∞)上是减函数.因此
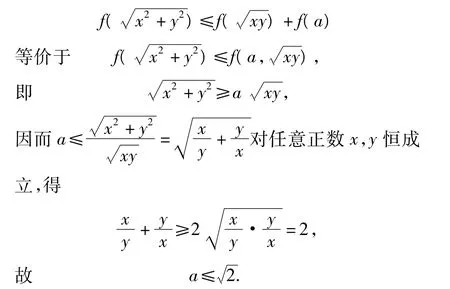
评注利用基本不等式求表达式的取值范围或最值,要注意其条件:“一正、二定、三相等”是否具备.
7 数形结合法
将不等式恒成立问题转化为函数图像的问题处理.



图1
评注借助函数的图像,往往能找到简捷、巧妙的解法.
数学的不等式恒成立问题形式多样,方法灵活多变,技巧性较强.这就要求我们要以变应变.在解题过程中,要根据具体的题设条件,认真观察题目中不等式的结构特征,从不同的角度、不同的方向,加以分析探讨,从而选择适当方法快速而准确地解出.因此,系统地掌握不等式恒成立问题的解题方法,无疑会对学生今后学习及培养学生分析问题和解决问题等方面有很大的帮助.

