稳定律吸引场中两两NQD列的Lr收敛性

沈建伟,王文胜

(1.浙江科技学院 理学院,浙江 杭州 310023;2.杭州师范大学 理学院,浙江 杭州 310036)

0 引 言

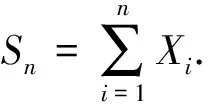
Eexp{itX1}=exp{-|t|α},t∈R.

(1)

称F属于指数为α∈(0,2)的稳定分布Gα的吸引场,如果存在常数An∈R,Bn>0使得

(2)

由文[1]定理2.2.8和推论2.2.17知式(2)成立当且仅当

(3)

定义称随机变量X和Y是NQD(Negatively Quadrant Dependent)的，若对∀x,y∈R都有

P(X

称随机变量列{Xn,n≥1}是两两NQD的，若对∀i≠j,Xi与Xj是NQD的.

两两NQD列的概念是由著名统计学家Lehmann[2]在1966年提出来的，由定义可以看出，两两NQD列是一类相当广泛的随机变量序列，通常的独立随机变量序列可以认为是两两NQD列的相当特殊的情形.后来的许多负相联的概念都是在此基础上繁衍出来的,著名的NA列[2]就是其特例之一.因此对两两NQD列的研究就显得更为困难.

Matula[3]对同分布两两NQD列部分和获得了与独立情形一样的Kolmogorov型强大数律.王岳宝等[4]在附加了某种混合条件后获得了同分布两两NQD列的Baum和Katz型完全收敛定理.吴群英[5]则去掉了文[4]中的混合条件对同分布两两NQD列部分和获得了与独立情形一样的Baum和Katz型完全收敛定理,并讨论了两两NQD列的三级数定理.陈平炎[6]获得了不同分布情形的Kolmogorov型强大数定律.万成高[7]讨论了两两NQD列的弱大数定律,在p阶Cesro一致可积相关条件下研究了两两NQD列的Lp收敛性和完全收敛性.

Pyke和Root[8]证明了对于独立同分布的随机变量序列{X,Xn,n≥1},如果0

(4)

其中如果0

此结果已被推广到了不同的情形,如当0

笔者证得了如下结果:

定理设{Xn,n≥1}是同分布的两两NQD列,有共同的分布函数F满足式(3),且对于∀n≥1,EXn=0.设1≤r<α<2,则

(5)

文中总设C代表正常数,在不同的地方可以代表不同的值.

1 定理的证明

定理的证明需要如下一些引理.

引理1[2]设随机变量X和Y是NQD的，则

i)EXY≤EXEY;

ii)P(X>x,Y>y)≤P(X>x)P(Y>y)，∀x,y∈R;

iii) 若f,g同为非降(或非增)函数，则f(X)与g(Y)仍为NQD的.

定理的证明对于1≤i≤n,记Ti=-s1/rI(Xi<-s1/r)+XiI(|Xi|≤s1/r)+s1/rI(Xi>s1/r),

则由引理1知Ti仍为两两NQD的.

注意到∀ε>0,

因此要证式(5),只需证明当n→∞时

及

如果X属于指数为α∈(0,2)的稳定分布Gα的吸引场,且0

对于I1,有

对于I2,由于∀n≥1,EXn=0,因此当n→∞时，

2n(εn)-1/rE|X1|I(|X1|>(εn)1/r)≤

2ε-1E|X1|rI(|X1|>(εn)1/r)→0.

从而当n足够大后,由Markov不等式及引理2有

对于

从而当n→∞时有

综上所述,定理得证.

[1] Embrechts P, Klüppelberg C, Mikosch T. Modelling extremal events for insurance and finance[M]. Berlin: Springer,1997：75-80.

[2] Lehmann E L. Some concepts of dependence[J]. Ann Math Statist,1966,37:1137-1153.

[3] Matula P. A note on the almost sure convergence of sums of negatively dependent random variables[J]. Statist Probab Lett,1992,15(3):209-213.

[4] 王岳宝,苏淳,刘许国.关于两两NQD列的若干极限性质[J].应用数学学报,1998,21(3): 404-414.

[5] 吴群英.两两NQD列的收敛性质[J].数学学报，2002,45(3):617-624.

[6] 陈平炎.两两NQD列的强大数定律[J].数学物理学报,2005,25A(3):386-392.

[7] 万成高.两两NQD列的大数定律与完全收敛性[J].应用数学学报,2005,28(2):253-261.

[8] Pyke R, Root D. On convergence inr-mean of Normalized Partial sums[J]. Ann Math Statist,1968,32(9):379-381.

[9] 陈平炎.两两NQD随机序列的Lr收敛性[J].数学物理学报,2008,28A(3):447-453.