线性空间直和分解定理的推广及应用

李毛亲

（台州学院 数学与信息工程学院，浙江 临海 317000）

线性空间直和分解定理的推广及应用

李毛亲

（台州学院 数学与信息工程学院，浙江 临海 317000）

把高等代数中线性空间的直和分解定理推广到一般情形.对于n维线性空间V上线性变换A的任一个化零多项式f（x），若f（x）为若干个两两互素的多项式的乘积，则线性空间V可以相应地分解成有限个A的不变子空间的直和.一些应用实例被给出.

线性空间；直和分解；多项式互素

在高等代数中，线性空间的直和分解定理是一个非常重要的定理，是研究矩阵对角化和Jordan标准形的理论基础.［1］中的直和分解定理如下：

定理1［1］设V是数域P上的n维线性空间，V上的线性变换A的特征多项式f（x）可以分解成互异的一次因式方幂的乘积

则V可以分解成s个A的不变子空间的直和

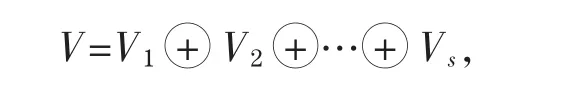
多项式g（x）称为线性变换A的化零多项式，若g（A）＝0.我们把定理1推广到A的任意化零多项式上去.

定理2 设V是数域P上的n维线性空间，若V上的线性变换A的化零多项式f（x）=f1（x）f2（x）…fs（x），f1，f2，…，fs两两互素，则V可以分解成s个A的不变子空间的直和

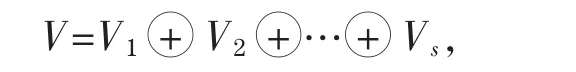
为证明该定理，我们首先给出两个引理，这两个引理除了在证明该定理时起重要作用外，本身也是重要的结论.

引理 1 设 f（x）=f1（x）f2（x）…fs（x），f1，f2，…，fs两两互素，则 g1，g2，…，gs互素，

证明 设（g1，g2，…，gs）＝d（x），考虑 d（x）/g1（x），由于 g1=f2…fs，若 d（x）≠1，可设 p（x）是 d（x）的一个不可约因式，由 p（x）/f2…fs可知，p（x）至少整除其中之一，不妨假设 p（x）|f2（x），考虑到 p（x）是 g1，g2，…，gs的一个公因式，得 p（x）|g2（x），于是 p（x）是 f2（x）和 g2（x）的公因式，但（f2（x），g2（x））=1，矛盾.所以 d（x）=1.

证明 对 Aα∈Ker fi（A），由于（fi（x），gi（x））=1，存在 P 上的多项式 ui（x），vi（x）使得

于是 ui（A）fi（A）α+vi（A）gi（A）α=α，由 fi（A）α=0，得

另一方面，对 Aα∈Imgi（A），存在 β∈V，使得 α=gi（A）β，fi（A）α=fi（A）gi（A）β＝f（A）β＝0，所以 α∈Kerfi（A），得

同理可以证明 Ker gi（A）=Im fi（A），i=1，2，…，s.

下面我们证明定理2.

证明 由引理 1，g1，g2，…，gs互素，存在多项式 u1，u2，…，us使得

所以对 α∈V，α=g1（A）u1（A）α+g2（A）u2（A）α+…+gs（A）us（A）α∈V1+V2+…+Vs.

再证明0向量的表示法唯一：

设 0=α1+α2+…+αs，αi∈Vi，i=1，2，…，s，则存在 βi∈Vi，使得 αi＝gi（A）βi，对等式 0=α1+α2+…+αs两端用gi（A）作用，由 gi（A）αj=gi（A）gj（A）βj=0（j≠i）得 gi（A）αi=0.再由引理 2 的（1）式可知，

所以，零向量表示法唯一，于是有

由于 gi（A）与 A 可交换，所以 Vi都是 A 的不变子空间，i=1，2，…，s.

下面的两个例子都是s=2时定理2的应用.

例1 设A是n维线性空间V上的幂等变换，A2=A，则

（1）V=Ker A+Im A＝W0+W1，其中Wλ为A的属于特征值λ的特征子空间；

（2）Aα∈Im A，Aα=α.

证明 （1）令 f（x）＝x2-x，f1（x）＝x，f2（x）＝x-1，则 f（x）＝f1（x）f2（x），且 f1（x）与 f2（x）互素，f（A）＝0，由定理 2，V=V1+V2，其中 V1＝Ker f1（A）＝Im f2（A），V2＝Ker f2（A）＝Im f1（A）.由于 f1（A）＝A，所以 V=Ker A+Im A.又V1=Ker A＝{α∈V|Aα=0}=W0，V2=Ker（A-E）＝{α∈V|Aα=0}=W1，所以 V=W0+W1.

（2）对 Aα∈Im A，由于 Ker（A-E）＝Im A=V2，得（A-E）α=0，Aα=Eα=α.

用完全类似的方法，我们可以得到对合变换的相关结论.

例2 设A是n维线性空间V上的对合变换，A2=E，则V=W1+W-1，其中Wλ为A的属于特征值λ的特征子空间.

证明 设 f（x）＝x2-1，f1（x）＝x-1，f2（x）＝x+1，则 f（x）＝f1（x）f2（x），且 f1（x）与 f2（x）互素，f（A）＝0，由定理 2，V=V1+V2，其中 V1＝Ker f1（A）＝Im f2（A），V2＝Ker f2（A）＝Im f1（A），且

所以，V=W1+W-1.

［1］北京大学数学系几何与代数教研室前代数小组.高等代数（第三版）［M］.北京：高等教育出版社，2003：309-311.

Generalized Theorem of Direct Sum Decomposition of a Linear Space and its Application

LI Mao-qin
(School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China)

In this paper,theorem of direct sum decomposition of a linear space in advanced Algebra is generalized.For any Annihilating polynomial f(x)of a linear transformation A,if f(x)is a product of finite mutually prime polynomials,linear space V could be decomposed into a direct sum of finite A-subspaces.Some applied examples are given.

linear space;direct sum decomposition;relatively prime of polynomials

耿继祥）

O151.2

A

1672-3708（2011）03-0001-02

2010-12-20

台州学院培育基金（2010PY011）.

李毛亲（1958- ），女，山西太原人，硕士，副教授，研究方向：应用数学及教学研究.

book=89,ebook=382