带有有序变量的结构方程模型中的模型选择

李云仙，王学仁

（1.云南财经大学 保险系，昆明 650021；2.云南大学 统计系，昆明 650091）

0 引言

有序分类数据在社会学、心理学、医学和行为学中非常常见，例如调查人们的疼痛不适感可由取值为1～5的有序变量来衡量 （其中1表示非常疼痛，2表示有些疼痛，3表示一般，4表示不疼痛，5表示感觉非常舒服）；人们在生活中的积极性同样可由类似有序变量来衡量。近年，很多学者对此类问题进行过研究，其中带有有序变量的结构方程模型[11]被广泛用于分析该类问题。在该类模型的应用过程中，一个主要问题就是如何寻找一个好的模型，使之能够较好的反映显变量、协变量和潜在变量之间的关系。因此，模型选择在结构方程模型的应用过程中是一个非常重要的问题。最近，贝叶斯方法在对结构方程模型的分析中受到了人们的极大关注[1]。其中，贝叶斯因子[2]是最常用的模型选择方法之一。由于该类模型结构复杂，贝叶斯因子的计算也比较困难[3]，为了解决这个问题，Gelman and Meng[4]提出了一种比较有效的路径抽样方法来计算一个概率密度函数的正态化因子。之后，这种方法就被广泛用于计算结构方程模型的贝叶斯因子[5][6]。然而，当两模型结构相差较大时，应用贝叶斯因子很难将这两个模型连接起来，这时就需要构造一些辅助模型。另外，众所周知，未知参数先验分布的选取在贝叶斯因子的计算中很重要。基于这些局限，本文将应用另外一个贝叶斯统计量，Lv测度[7]，对带有有序分类变量的结构方程模型进行选择。测度是一种基于贝叶斯准则的方法，但对参数的先验信息没有严格要求；同时，Lv测度的计算非常简单，可克服贝叶斯因子的一些缺陷。

1 Lv测度在带有有序分类变量的结构方程模型中的应用

1.1 Lv测度的定义

其中

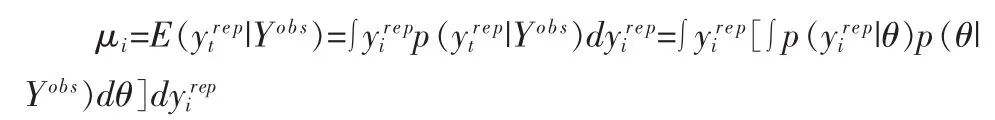
v（0≤v≤1）为权重系数，当 v=1时，该准则等价于平方残差和。从式（1）给出的定义，Lv测度包括两部分，第一部分为后验预测方差，可以看成是惩罚项；第二部分为预测偏差，可以看成是对模型的拟合优度的测量。因此，具有最小Lv测度的模型被认为是最优模型。

1.2 模型定义

假设 yi（i=1，…，n）是一个 p×1 的随机向量，同时 yi满足以下测量方程：

其中 u（p×1）表示均值向量，ωi（q×1）表示关于潜在变量的随机向量，Λ（p×q）表示载荷矩阵，εi～N（0,Ψε）表示残差向量，其中 Ψε=diag（ψε1，…，ψεp）是一个对角阵。同时，假设 ωi和εi是相互独立的。 潜在变量 ωi可以进一步分解为由此可以定义测量潜在变量间关系的结构方程为：

其中 ηi（ q1×1）为内生潜在变量，ξi（q2×1）为外生潜在变量，q1+q2=q；F（ξi）=（ f1（ξi），…， fm（ξi））T为包含 m 个实值可微函数的向量，其中m≥q。另外，假设Π0=Iq1-Π是一个正定矩阵，同时该矩阵的行列式与 Π 中的元素无关；ξi～N（0，Φ）与δi～N（0，Φδ）相互独立，其中 Φδ=diag（ψδ1，…，ψδq1）。 如果令 Λω=（Π，Γ），以及那么式（3）可改写为 ηi=ΛωG（ωi）+δi。 另外，如果令 Λη和 Λξ分别为对应于 ηi和 ξi的Λ的两个子矩阵，由式（2）和（3）定义的结构方程模型可以改写为 yi=u+ΛηΠ0（ΓF（ξi）+δi）+Λξξi+εi。

为了处理有序分类变量，假设 yi=（yo，i，yu，i），其中 yo，i（r×1）为可观测连续随机向量，yu，i（s×1）为不可观测连续随机向量，r+s=p。其中关于yu，i的信息可以通过可观测有序分类变量zi（s×1）得到，它们之间的关系定义如下:

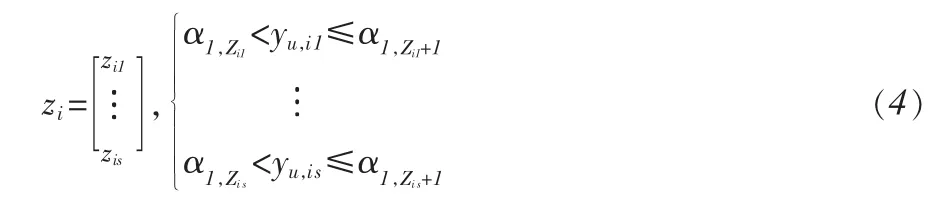
其中 zik（k=1，…s）为在{0，1，…，bk}中取值的整数，αk=（αk，0，…，αk，bk+1）（k=1，…，s）表示阀值。 因此，对于第 k 个变量，根据阀值所定义的类别就有bk+1类。在该模型中，一般假定 αk，0=-∞，αk，bk+1=∞。 根据很多学者的研究，为了确保模型的可识别性，αk，1和 αk，bk，以及Λ和Π中部分元素的值会预先给定。为了方便起见，记式（2）到（4）定义的模型为M。

1.3 带有有序分类变量的结构方程模型中的测度

为了定义上述出模型的 Lv测度， 令其中，表示可观测连续变量的样本矩阵Yu=（yu，1，…，yu，n），为不可观测连续随机变量的样本矩阵同时令令为有序分类变量的样本矩阵，其中

根据这个定义可得，p（zik，j=1）=p（zik=j-1）=p（αk，j-1＜yu，ik≤αk，j）▯pik，j，以及 p（zik，j=0）=1-p（zik，j=1）=1-pik，j。 从上面的定义可知，zik，j～Bernoulli（pik，j），其分布函数为：

f（zik，j，pik，j）=（pik，j）zik，j（1-pik，j）1-zik，j因此，本模型中的观测数据即为令和 Zrep分别为 Yobs和 Zobs的预测值。 此外，令 Ω =（ω1，…，ωn），Ω1=（η1，…，ηn），Ω2=（ξ1，…，ξn），α 为包括所有阀值的向量，θ为包括模型中所有未知参数的向量。

在上面介绍的Lv测度是基于指数分布族定义的，由于本模型包括两类变量，连续变量和有序分类变量。根据模型的定义，连续变量的分布属于指数分布族，可以直接应用式（1）给出的Lv测度。然而，有序分类变量的分布并不属于指数分布族，因此式（1）给出的Lv测度不能直接应用。为了解决这个问题，本文将采用Chen,Dey and Ibrahim[8]给出的一种方法将有序分类数据转化成二元数据。引入一个新的bk+1的向量，其中的元素定义为：

此分布属于指数分布族，且该分布的期望和方差分别为

E（zik，j）=pik，j，Var（zik，j）=pik，j（1-pik，j）

根据式（5），可将Zobs和Zrep中的数据全部转换成来自伯努利分布的数据，转化后的数据分别用Zobs*和Zrep*表示。对于有序分类数据，定义如下二次损失Lv测度（quadratic loss Lvmeasure）[8]：

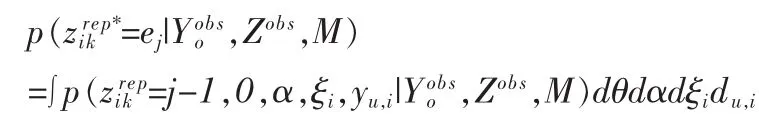
其中，ej是一个bk+1维列向量，除了第j个元素为1，其他元素全部为0。在上式中

通过简单变换，式（6）可写为

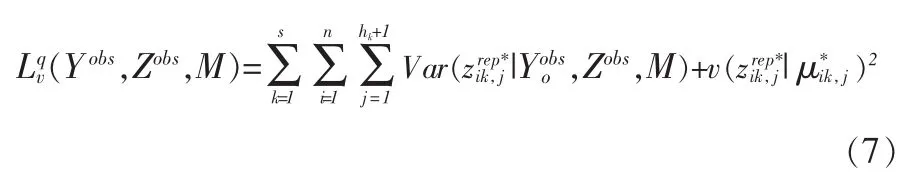
M）+的第 j个对角元素是条件期望的第j个元素。故

根据模型的定义，在θ和ξ给定的条件下，yu，i具有正态分布，其均值为协方差阵为 Λu，η（1ΓF（ξi）T）+Ψεu，其中 uu，Λu，η，Λu，ξ和 Ψεu分别为 u，Λη，Λξ和Ψε的对应于yu，i的子向量或子矩阵。式（8）中最后一个概率函数为：

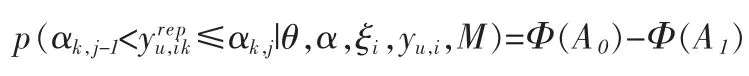
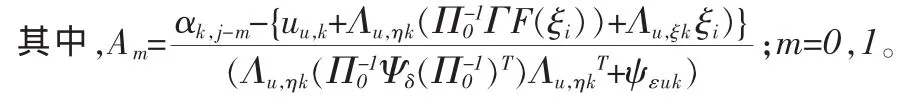
uu，k为 uu的第 k 个元素，Λu，ηk和 Λu，ξk分别为 Λu，η和 Λu，ξ的第 k 行，ψεuk为 Ψεu的第 k 个对角元素，Φ（·）表示标准正态分布的累计分布函数。根据上面的公式便可以得到式（7）中的条件期望。根据这个条件期望，可以进一步得到式（7）中的条件方差：

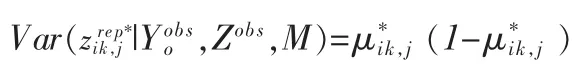
对于模型中的连续变量，由式（1）定义的Lv测度可以直接采用。因此，本文定义的模型M的Lv测度为：

其中 uo，k为 uo的第 k 个元素，Λo，ηk和 Λo，ξk分别为o，η和Λo，ξ的第k行。式（9）中第一个求和项中的条件方差为：

至此，在式（9）中需要的条件期望和方差都得到了，然而在求这些条件期望和条件方差的过程中需要求高阶积分，而这些积分是没有办法求出来的，因此不能得到Lv测度的显式表达式。本文将采用MCMC的方法来计算Lv测度。

根据 Lv测度的定义，只要得到关于（θ，α，Ω，Yu）的一个足够大的后验样本，Lv测度就可以计算出来了。本文将采用Gibbs抽样[9]从后验分布中抽取所需要的样本。 具体为，给定当前数值（θ（g），α（g），Ω（g），）：

在这个方法收敛后就可以得到关于未知参数、潜在变量、阀值、不可观测变量的后验样本{θ（g），Ω（g），α（g），Yu（g）；g=1，…，G}，G是一个足够大的数据。参数和潜在变量的后验均值可以作为他们的贝叶斯估计值，而Lv测度也可以根据这个后验样本得到。

根据前面的讨论，要完成Gibbs抽样，计算测度的值，就需要求出关于位置参数以及潜在变量，阀值等的后验分布。首先，对于Gibbs抽样的第一步，需要给出未知参数的先验分布。本文将采用以下常用的共轭先验分布：

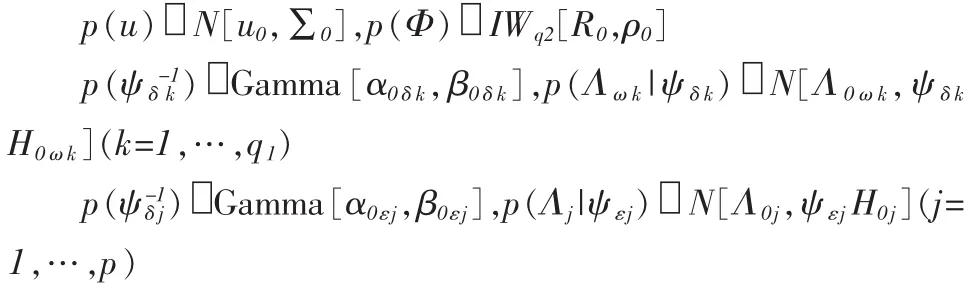
其中IWq2表示q2维数为逆Wishart分布，在上述先验分布中 ρ0，α0δk，β0δk，α0εj，β0εj，u0，Σ0，Λ0ωk，H0ωk，Λ0k和 H0k是根据先验信息预先给定的一些超参数。根据这些先验分布，可以很容易的求出关于它们的后验分布，这些后验分布都是比较熟悉的正态分布，伽马分布，Wishart分布，从这些分布中抽取随机数比较简单。为了节省空间，这里将不给出具体的推导过程。对于阀值α，本文将采用如下无信息先验分布：

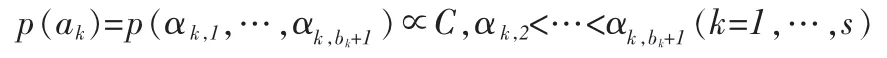
其中 C 是一个常数。 令 yu（k）=（yu，1k，…，yu，nk），由此可得

根据前面的讨论，在Gibbs抽样中①中所需要的条件分布是比较常见的分布，可以直接从这些后验分布中抽取未知参数的随机数。然而，②和③中所需要的后验分布均是不常见的分布，从这些分布中抽取随机数就比较复杂。为了解决这个问题，Metropolis-Hastings（MH）方法[10][11]将被应用与随机抽样。因此，本文所采用的MCMC算法是Gibbs抽样和MH方法的一种混合算法。

2 实例分析

生活质量（quality of life,QOL）的度量在临床实验以及与健康相关的分析中非常重要，在这个问题中，有序分类变量比较常见。针对这个问题，Lee[12]将带有有序变量的结构方程模型应用到该问题中进行过分析，并应用贝叶斯方法估计结构方程模型的未知参数。本文将同样采用带有有序分类变量的结构方程模型对QOL数据进行分析，然而本文的目的在于应用测度进行模型选择。WHOQOL－100量表（世界卫生组织生存质量测定量表）是世界卫生组织20余个国家和地区共同研制的适用于一般人群的普适性量表。该量表主要用于评估四个潜在变量的状况：身体健康ξ1，心理健康ξ2，社会关系ξ3及环境影响ξ4，以及一个关于总体健康状况（z1）及精神支柱（z2）的综合因素η。这四个潜在变量可以由24个小方面（z3～z26）来反映，它们之间的关系为：z3～z9反映人的身体健康状况，z10～z15反映人的心理健康状况，z16～z18反映社会关系，z19～z26反映环境因素。根据问题设计，这26个变量均为有序分类变量，其取值均为1～5（其中1表示完全不满意，2表示有些不满意，3表示适度，4表示满意，5表示非常满意）。整个样本数据量非常大，这里只是为了说明本文所提出的方法在模型选择中的应用及效用，只分析样本容量n=338的一组综合数据。本例将比较两个结构方程模型：M1和M2，其中M1的定义如下：

M1：y=Λ1ω1+ε，η=γ1ξ1+γ2ξ2+γ3ξ3+γ4ξ4+ε

其中载荷矩阵为：

模型M2定义为：

M2：y= Λ2ω2+ε，η=γ1ξ1+γ2ξ2+γ3ξ3+γ4ξ4+ε

其中载荷矩阵为:

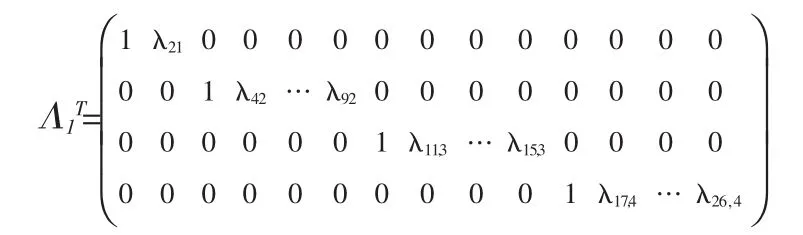
ω2=（η，ξ1，ξ2，ξ3），即将社会关系领域及环境领域合为一个因素。 在该模型中，假设，ε～N［0，Ψε2］，ξ＝（ξ1，ξ2，ξ3）～N［0，Φ2］，δ～N［0，］。

在上面两个模型中，y=（y1，…，y26）T是隐含的连续变量，其信息可通过式（4）由观测变量 z=（z1，…，z26）T得到。其中，阀值为 α =（α1，…，α26），αk=（αk1，αk2，…，αk5，αk6）（k=1，…26），αk1=-∞，αk6=∞。为了使模型可识别，需要固定αk2和αk5为一定值，本文采用标准正态分布来确定αk2和αk5的给定值。具体做法为，分别计算zk=1概率p1以及zk=5概率p5，则根据标准正态分布，可以设定 αk2=Φ-1（ p1），αk5=Φ-1（ p5），其中 Φ-1表示标准正态分布累计分布函数的反函数。

为了计算Lv测度，需要给定共轭先验分布中先验信息，即超参数的取值。本例给定如下先验信息：对于Λ1和Λ2中未知元素的先验分布的均值均设定为 0.8，对应于（γ1，γ2，γ3，γ4）的先验分布均值设为（0.6，0.6，0.4，0.4），Φ1和 Φ2的先验分布，逆wishart分布中的超参数为8I3，其中 Id表示 d 维单位阵，关于 Ψε1和 Ψε2中的元素，先验分布为伽马分布，其中的超参数为 α0εk1=α0εk1=10，β0εk1=β0εk1=8，而对于 σ1δ和 σ2δ的先验分布，超参数为 α0δ1=α0δ2=10 α0δ1=α0δ2=10。 本文将采用 R2WinBUGS 来计算 Lv测度，其中，所用样本为Gibbs抽样过程中删除前4000次之后的2000次抽样构成。在时，计算结果为：

L0.5=（M1）=7273.01，L0.5=（M2）=7343.82

因此，本文认为模型M1优于M2。

为了比较不同模型选择方法的结果，本文还针对此例计算了贝叶斯因子，得logB12=23.51，根据贝叶斯因子在模型选择中的准则,同样选择模型。

3 结论

本文将Lv测度应用到带有有序分类变量的结构方程模型中进行模型选择，并通过一个实例分析说明了该方法的有效性。从实例分析可以看出，Lv测度与贝叶斯因子可以得出相同的结论。然而，Lv测度的计算比贝叶斯因子简单且节省时间，并对参数先验分布没有严格要求。本文所考虑的Lv测度均是基于v=0.5得到的，当然的取值可以在内变化，针对此问题，作者也试过使取其它值，但结果变化不大，因此本文仅给出v=0.5的结果。

其次，Lv测度的应用比较广泛，除本文提出的模型及数据类型外，还可以将其应用到其他一些诸如带有无序分类变量的结构方程模型的模型选择以及其类型的模型。同时，v的最优取值也是一个比较有意义的研究问题。

[1]R.Schines,H.Hoijtink，A.Boomsma.Bayesian Estimation and Testing of Structural Equation Models[J].Psychometrika，1999，（64）.

[2]R.E.Kass，A.E.Raftery.Bayes Factors[J].Journal of the American Statistical Association，1995，（90）.

[3]T.J.DiCiccio,R.E.Kass,et.al.ComputingBayesFactorsby Combining Simulation and Asymptotic Approximations[J].Journal of the American Statistical Association，1997，（92）.

[4]A.Gelman，X.L.Meng.Simulating Normalizing Constantsfrom Importance Sampling to Bridge Sampling to Path Sampling[J].Sta tistical Science，1998，（13）.

[5]S.Y.Lee，X.Y.Song.Bayesian Model Comparison of Nonlinear Structural Equation Models with Missing Continuous and Ordinal Categorical Data[J].British Journal of Mathematical and Statistical Psychology，2004，（57）.

[6]S.Y.Lee，N.S.Tang.Bayesian Analysis of Structural Equation Models with Mixed Exponential Family and Ordered Categorical Data[J].British Journal of Mathematical and Statistical Psychology，2006，（59）.

[7]J.G.Ibrahim,M.H.Chen，D.Sinha.Criterion-based Methods for Bayesian Model Assessment[J].Statistica Sinica，2001，（11）.

[8]M.H.Chen,D.K.Dey，J.G.Ibrahim.Bayesian Criterion Based Model Assessment for Categorical Data[J].Biometrika，2004，（91）.

[9]S.Geman,D.Geman,Stochastic Relaxation,Gibbs Distribution,and the Bayesian Restoration of Images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，（6）.

[10]N.Metropolis,A.W.Rosenbluth,M.N.Rosenbluth,et.al.Equa tions of State Calculations by Fast Computing Machine[J].Journal of Chemical Physics，1953，（21）.

[11]W.K.Hastings. Monte Carlo Sampling Nethods Using Markov Chains and Their Application[J].Biometrika，1970，（57）.

[12]S.Y.Lee. Structural Equation Modeling:A Bayesian Approach[M].New York:Wiley，2007.