抽象数据类型的双代数结构*

苏锦钿 余珊珊

(1.华南理工大学计算机科学与工程学院，广东广州510006;2.中山大学信息科学与技术学院，广东广州510275)

传统的抽象数据类型(ADT)以归纳数据类型为主，侧重于数据类型的有限语法构造，一般包含一些称为“构造子”的操作，有限分支树、数组、队列、堆栈、自然数等都是典型的归纳数据类型.在范畴论的视角下，每个归纳数据类型都可以抽象地描述为某个代数函子下的初始代数，其中代数函子对应该数据类型的构造操作，因此，归纳数据类型也常被称为代数数据类型［1-2］.由初始代数的初始性可得到归纳数据类型上的一个递归操作，称为Fold射［3］.该操作满足一系列的代数计算定律，在程序的计算及转换研究中具有重要的作用.

共归纳数据类型［4］也称为共代数数据类型［5］或共数据类型［6］，可看作是归纳数据类型的范畴对偶概念，无限分支树、无限链表和流等都是典型的共归纳数据类型.与归纳数据类型不同，共归纳数据类型侧重于数据类型在计算过程中所展现出来的动态行为.在范畴论的视角下，这一类数据类型可进一步抽象为某个共代数函子下的终结共代数，其中共代数函子对应该数据类型上的观察操作.由终结共代数的终结性可得到共归纳数据类型上的一个共递归操作，称为Unfold射［7］.该操作满足一系列的共代数计算定律，在基于行为特征的函数定义和程序推理及转换过程中具有重要的作用［6，8］.

对许多ADT(例如流、链表、堆栈和树等)来说，除了本身包含可由代数进行描述的语法构造特征外，同时还包含可由共代数进行描述的动态行为特征，即同时具有归纳和共归纳数据类型的特点.因此，单纯利用代数或共代数只能刻画其中某一方面的特征.

代数和共代数本质上都可看成是集合及其上满足一定性质的操作.从范畴论的角度看，两者之间存在共同点，可以通过某种合适的关系融合在一起.基于上述考虑，Rutten等［9］提出了双代数作为代数与共代数的一种融合，其中代数函子给出基集元素的构造方法，刻画了系统的语法构造特征，而共代数函子给出基集元素的行为变迁结构，刻画了系统的动态行为语义.目前，双代数主要应用于程序语言的操作语义与指称语义研究中［10-11］，被证明是研究状态系统静态结构与动态行为的性质及两者间关系的一种可行途径.

许多ADT都可以看成是一个典型的双代数结构:ADT上的语法构造操作可以表示成某个代数函子下的基调，这是典型的代数结构;而ADT在计算过程中所展现出来的动态行为可以表示为某个共代数函子下的行为变迁结构，这是典型的共代数结构.代数和共代数函子间通过称为分配律的自然转换有机地联系起来.这种分配律一方面给出构造操作与产生合适行为之间的关系，另一方面可通过函子化提升分别研究递归函数与共代数结构、共递归函数与代数结构的性质及两者间的关系，从而扩展了代数中的归纳原理和共代数中的共归纳原理.

Erwig［12-13］指出ADT可以表示成双代数结构，并探讨了以共代数函子为参数的递归操作，从而提出一种 Metamorphic编程风格.Nogueira等［14］也指出ADT可以表示成双代数结构，并探讨了ADT的双代数结构在多态编程中的应用.但 Erwig和Nogueira等均没指出如何分析ADT上的语法构造和动态行为的性质及两者间的关系，也没有说明如何利用函子化提升研究递归和共递归函数.

相对于上述研究，文中利用双代数研究ADT上的语法构造和动态行为之间的关系，给出了ADT的一种双代数结构，并说明了如何通过分配律对共代数和代数函子进行提升，从而将共代数结构(或代数结构)融入到递归(或共递归)函数的定义及计算中，进一步扩展了代数中的归纳原理和共代数中的共归纳原理，提高了程序语言对ADT中各种性质的描述与证明能力.

1 抽象数据类型的双代数结构

双代数是同一载体集上的代数和共代数对，其定义如下.

定义1 给定范畴C上的两个自函子F和B，一个〈F，B〉-双代数为一个三元组(X，αX，βX)，其中X为载体集，αX:FX→X和βX:X→BX分别为同一载体集X上的F-代数结构和B-共代数结构:

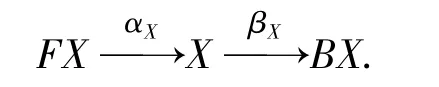
两个〈F，B〉-双代数(X，αX，βX)和(Y，αY，βY)之间的同态射是一个射f:X→Y，且满足图1中的图表交换.

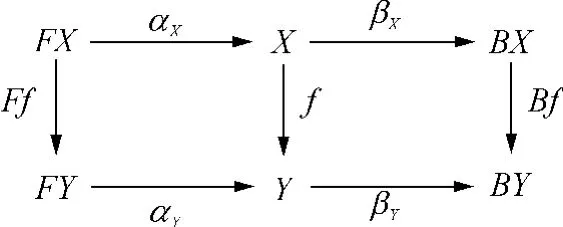
图1 双代数同态射Fig.1 Homomorphism between bialgebras

因此，双代数同态射可以看成同时为对应的F-代数和B-共代数之间的同态射.范畴C上所有的〈F，B〉-双代数及其同态射可构成一个范畴，记为C(F，B).

〈F，B〉-双代数给出了同一个基集上的代数操作和共代数行为变迁结构，但没有说明两者间的变换关系，因此无法直接用于描述ADT.下面进一步给出λ-双代数的定义.

定义2 设F和B分别为代数函子和共代数函子.则F对B的一个分配律为一个自然转换λ:FB⇒BF.双代数上的分配律λ简称为λ-双代数，是一个〈F，B〉-双代数(X，αX，βX)，且满足图 2 中的图表交换.

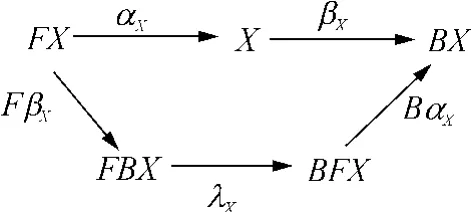
图2 λ-双代数Fig.2 λ-bialgebras

包含所有λ-双代数的范畴构成了范畴C(F，B)的一个完全子范畴，记为Cλ(F，B).Cλ(F，B)具有一些重要的性质，例如在合适的条件下每一个λ-双代数上的互相似是同余关系，因此其初始语义与终结语义是一致的［9］.

根据图2中的图表交换，λ-双代数通过分配律将双代数结构中的代数运算和共代数行为变迁有机地融合在一起.即一方面代数上的构造操作是具有良行为的操作，另一方面共代数上的行为变迁在这些构造操作下被保持.

下面给出一些典型的ADT的双代数结构.

例1 实数流 R∞上的前缀操作 scons:R×X→X表示将一个实数作为前缀添加到一个流中，加法操作⊕:X×X→X和乘法操作⊗:X×X→X分别表示将两个流中对应位置的元素相加或相乘后构成一个新的流.上述构造操作可表示为一个代数结构:(X，αX=［scons，⊕，⊗］:R ×X+X×X+X×X→X).

对实数流中的元素进行观察的操作包括:value:X→R用于得到流当前状态上的实数，next:X→X用于让流进行下一个状态.上述观察操作可表示为一个共代数结构(X，βX=〈value，next〉:X→R ×X).

因此，实数流R∞可描述成一个双代数结构:(X，αX:R×X+X×X+X×X→X，βX:X→R×X).

例2 参数化链表List［A］(A是某个已知数据类型)上的空链表nil:1→X和插入操作cons:A×X→X为构造子，用于构造所有的有限链表，合并操作zip:X×X→X用于依次将两个链表中的头元素取出后合并成一个新的链表.上述构造操作可表示为一个代数结构:(X，αX=［nil，cons，zip］:1+A×X+X×X→X).

观察操作head:X→A+1和tail:X→X+1分别给出了链表中的头元素及除头元素外的剩余部分;若链表为空，则返回*∈1.上述观察操作可表示为一个共代数结构(X，βX=〈head，tail〉:X→A×X+1).

因此，链表List［A］可描述成一个双代数结构:(X，αX:1+A×X+X×X→X，βX:X→A×X+1).

双代数同态射f:A→E用于将链表List［A］中的元素类型由A转换为E，并且在转换的过程中保持代数及共代数操作.

类似地，对于树、堆栈、队列或集合等其它ADT，也可以建立相应的双代数结构.事实上，程序语言中任意的归纳或共归纳数据类型都可以通过适当的扩展构成一个双代数结构.

例如，由集合范畴Set上的类型构造子FX=1+X的初始代数可以得到归纳数据类型N(表示自然数)，基调inF=［zero，succ］包括了初始化操作zero:1→N和后继操作 succ:N→N.逆=〈iszero，pred〉给出了自然数上的观察操作，其中iszero:N→1表示自然数为0，而pred:N→N给出了某个非零自然数的前驱.因此，(N，inF=［zero，succ］，=〈iszero，pred〉)就是自然数N上的一个双代数结构.由集合范畴Set上的自函子BX=R×X的终结共代数可以得到共归纳数据类型中的实数流R∞的定义，基调outB=〈value，next〉分别给出实数流的当前值及后继状态.逆=［scons］为实数流上的一个构造操作.因此，(R∞=［scons］，outB=〈value，next〉)就是实数流上的一个双代数结构.

给定 ADT 的一个λ-双代数结构(X，αX，βX)，可以进一步利用分配律λ:FB⇒BF刻画X上的语法构造和动态行为之间的转换关系.

例3 分配律λ:FB⇒BF自然地描述了链表List［A］(记为A*)上的语法构造与动态行为之间的关系.例如，对cons操作来说，下面的交换图(图3)给出了链表变量［2，1，0］上的构造和观察之间的变换关系，其中Id为标识函子.

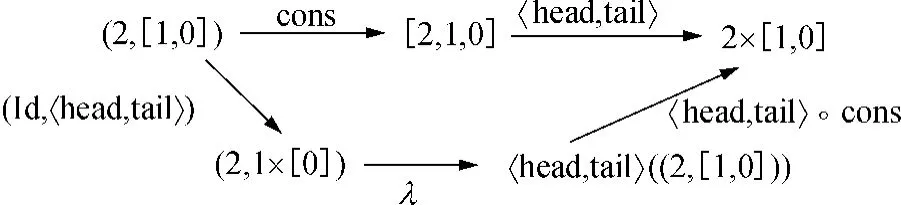
图3 链表上的λ分配律例子Fig.3 An example ofλ-distributive law on lists

假设σ不为空，且σ=a'·σ'(σ，σ'∈A*;a，a'∈A)，则链表上的 cons与〈head，tail〉之间的转换关系为

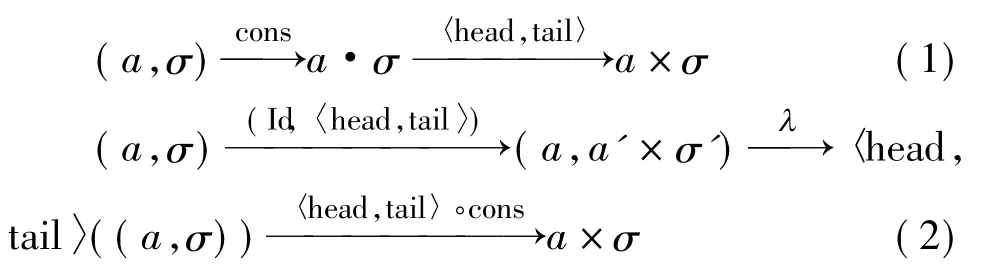
式(1)和(2)的结果是相同的，即当利用cons操作在链表σ中插入一个元素a后，可以采用以下两种方式:

(1)先利用cons将一个元素a插入到现有的链表σ中，然后再通过head和tail对其进行观察并得到结果a×σ;

(2)在保持cons操作的代数结构的前提下利用head和tail对σ进行观察得到(a，a'×σ')，接着通过λ分配律将(a，a'×σ')转换成〈head，tail〉((a，σ))，最后在保持共代数行为变迁结构的前提下利用cons得到a×σ.

这两种方式所得到的结果都是一样的，即先构造后观察与先观察后转换再构造的结果是相同的，并且这两种方式与链表中所包含的元素的实际类型无关，即体现了λ的自然性特点.

2 分配律与函子化提升

2.1 共代数函子提升

给定一个 ADT 的λ-双代数结构(X，αX，βX)，利用分配律λ:FB⇒BF可对共代数函子B进行函子化提升.

定义3 由分配律λ:FB⇒BF可定义一个共代数函子Bλ，将B:C→C提升为Bλ:CF→CF，使得对任意一个F-代数(X，αX)有Bλ(X，αX)=(BX，BαX◦λ X:FBX→BX)，对任意一个代数同态射h:(X，αX)→(Y，αY)有Bλh=Bh.

由文献［15］中的定理15.3 可知Bλ是(BX，BαX◦λX)和(BY，BαY◦λY)间的代数同态射，因此这种提升是函子化的.Bλ相当于把文献［16］中的λ提升作用于共代数函子B:将X提升为BλX=BX，将αX提升为BλαX=BαX◦λX.载体集BX是以X中的元素为参数变量、以B中的基调为观察操作所得到的行为变迁结构，而分配律λ则说明了如何在给定变量X的F-代数结构的前提下为其行为结构BX中的元素添加相应的F-代数结构.

每一个提升后的代数Bλ(X，αX)给出了变量X的共代数行为变迁结构上的F-代数结构，且存在从初始代数(μF，inF)到Bλ(X，αX)的唯一射其中μF是初始代数的载体，且为基调inF上的最小不动点.使得等式◦inF=BλαX◦F成立，即满足图4所示的图表交换.

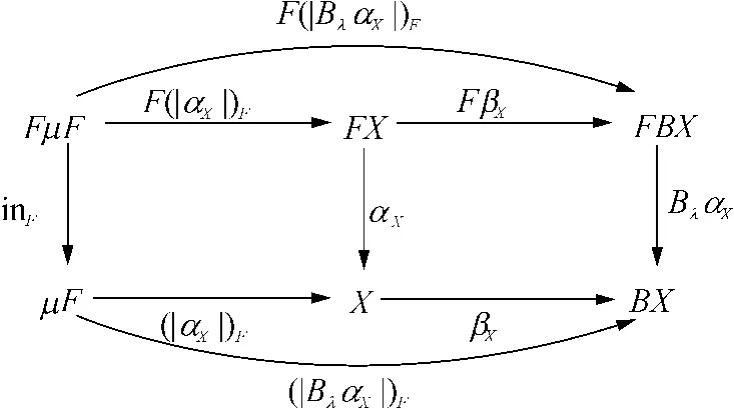
图4 初始代数到BλαX的Fold射Fig.4 Fold morphisms from initial algebras to BλαX

定理1 上述的λ-Fold射满足

证明 由Fold射及函子化提升的性质可知图4中的各个图表均满足交换，因此和均为从初始代数(μF，inF)到Bλ(X，αX)的Fold射.再由Fold射的唯一性可知有

例4 函数double:A*→A*将链表中的每个元素分别乘以2后构成一个新的链表，即对于σ，r∈A*和a∈A，double定义如下:

double(nil)=dnil=［］，

double(cons(a，σ))=dcons(a，double(σ))=

cons(a×2，double(σ))=a×2:double(σ)，

double(zip(σ，r))=dzip(double(σ)，double(r))=

cons(2 ×head(σ)，double(zip(r，tail(σ))))=

2 ×head(σ):double(zip(r，tail(σ))).

显然，double 是初始代数(A*，［nil，cons，zip］)与代数(A*，［dnil，dcons，dzip］)间的一个 Fold 射

利用分配律λ可将(A*，α=［dnil，dcons，dzip］)提升为Bλ(A*，α)=(BA*，Bλα)，其中Bλα=［nl，cs，zp］，从而得到λ-Fold 射如图5所示.

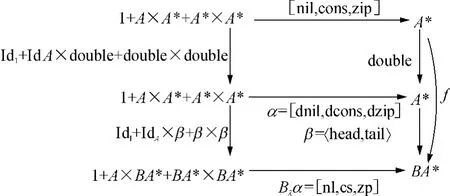
图5 链表上的λ-Fold射例子Fig.5 An example ofλ-Fold morphisms on lists

f定义如下:

f(nil)=nl=［］，

f(cons(a，σ))=nl(a，f(σ))=〈2 ×a，f(σ)〉，f(zip(σ，r))=zp(f(σ)，f(r))=

〈2 ×head(σ)，f(zip(r，tail(σ)))〉.

上述的λ-Fold射f递归地给出了链表σ在函数double作用下所得到的像的共代数行为变迁结构，从而将一般的Fold射扩展到共代数行为变迁结构上.

对于初始代数(μF，inF)，利用λ可将其提升为Bλ(μF，inF)=(BμF，BλinF=BinF◦λμF:FBμF→BμF)，且存在λ-Fold 射如图6所示.

图6 初始代数到BλinF的Fold射Fig.6 Fold morphisms from initial algebras to BλinF

证明 由λ-双代数及函子化提升的性质可知图7的各个图表均满足交换.对于任意的(X，αX)及Fold射由文献［15］中的定理15.3可知是从(BμF，BλinF)到(BX，BλαX)的代数同态射和均为从(μF，inF)到(BX，BλαX)的λ-Fold射，由其唯一性有因此是μF上的一个B-共代数结构与(X，βX)间的共代数同态射，而且(μF，为初始B-共代数.再由文献［17］中的定理3.2.3可知为(μF，inF)上唯一的共代数结构，且为初始λ-双代数.

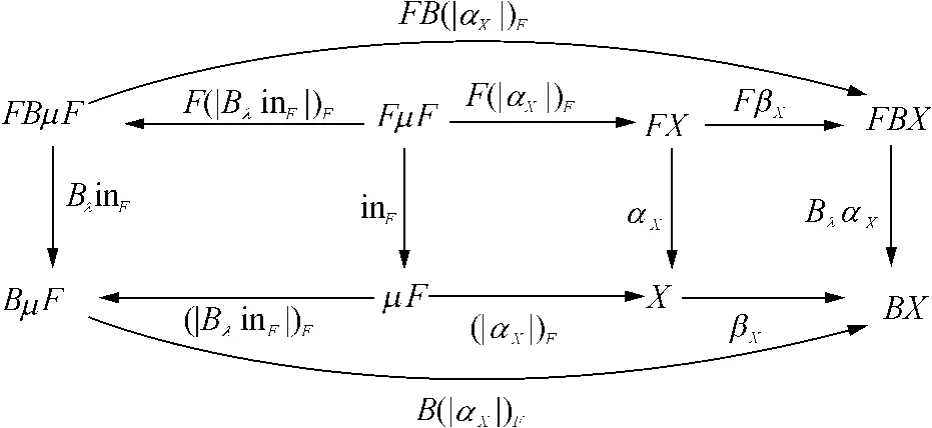
图7 初始代数的λ-提升Fig.7 λ-lifting of initial algebras

上述定理给出了一种利用分配律λ:FB⇒BF及Fold射构造初始代数上的共代数结构的方法，从而将初始代数提升为相应的初始λ-双代数.

2.2 代数函子提升

利用分配律可以将具有共代数行为变迁结构的变量提升为以该变量为参数的代数项上的共代数结构.

定义4 由分配律λ:FB⇒BF可定义一个代数函子Fλ，将F:C→C提升为Fλ:CB→CB，使得:对于任意一个共代数(X，βX)有Fλ(X，βX)=(FX，λX◦FβX:FX→BFX)，对于任意一个共代数同态射h:(X，βX)→(Y，βY)有Fλh=Fh.

容易验证Fh是共代数(FX，λX◦FβX)和(FY，λY◦FλY)间的同态射［15］，而Fλ可看成是对代数函子F的一种λ提升［16］:将X提升为FλX=FX，将βX提升为FλβX=λX◦FβX，将h:(X，βX)→(Y，βY)提升为Fλh=Fh:(FX，FλβX)→(FY，FλβY).显然，这种提升是函子化的.FX中的元素是以参数X中的元素为变量，以F中的方法为构造操作所得到的代数项，且X具有B-共代数结构.而分配律λX说明了如何在给定参数X的共代数行为变迁结构的前提下对FX中的元素指派相应的共代数行为变迁结构.

每一个提升后的共代数Fλ(X，βX)给出了代数项上的共代数行为变迁结构，且存在到终结共代数(vB，outB)的唯一射[FλβX]B，其中vB为终结共代数上的载体，且为基调outB上的最大不动点.[FλβX]B使得等式 outB◦[FλβX]B=B[FλβX]B◦FλβX成立，即满足图8中的图表交换.

[FλβX]B是由基调FλβX所确定的一个 Unfold射，称为λ-Unfold射.

定理3 上述λ-Unfold 射满足[FλβX]B=[βX]B◦αX.

证明 显然，[FλβX]B和[βX]B◦αX均为从共代数(FX，FλβX)到终结共代数(vB，outB)的λ-Unfold 射，由其唯一性可证上述等式成立.

例5 利用分配律λ可将实数流共代数(X，βX:X→R ×X)提升为(FX，FλβX=λX◦FβX:FX→BFX)(见图9).对实数流上的代数项(σ⊕r)⊗w，(其中σ，r，w∈R∞)，λ-Unfold 射f=[FλβX]B的定义如下:

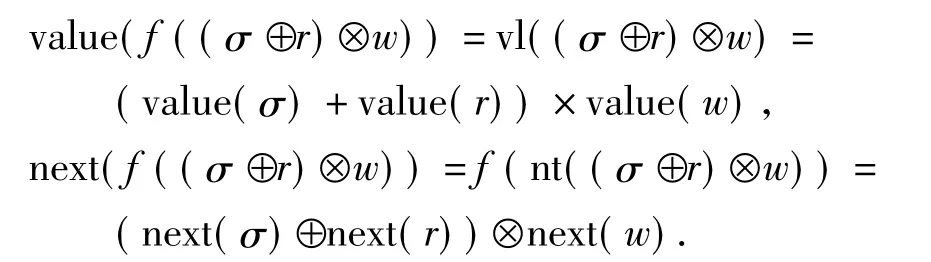
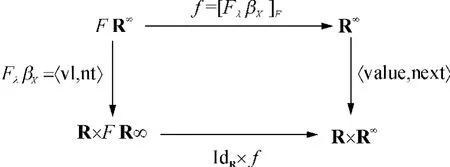
图9 实数流共代数的λ-提升Fig.9 λ-lifting of stream coalgebras for real numbers

λ-Unfold射[FλβX]B给出了代数项与该项在共代数函子下的全局行为之间的映射关系，从而将定义在变量X上的一般Unfold操作扩展到以该变量X为参数的代数项上，并从行为观察的角度给出了代数项的全局行为的共递归定义.

由λ-Unfold射的唯一性及终结共代数上的互模拟是等价关系的性质可以得到一种基于共归纳原理的证明代数项相等的方法:即要证明项代数FX中的任意两个元素是相等的，只需证明它们在[FλβX]B的作用下映射到终结代数中的同一状态上.这实际上是将一般变量X上的共归纳证明原则扩展到以该变量为参数的代数项上，从而为代数项的相等性提供了一种基于行为观察的证明方法，并扩展了共代数中的共归纳原理，同时与传统的基于归纳原理的证明方法形成互补.

例6 要证明实数流上的操作⊕满足对⊗的分配律，即∀σ，r，w∈R∞.(σ⊕r)⊗w=(σ⊗w)⊕(r⊗w)，由终结共代数上的互模拟是等价关系的性质可知，只需证明存在某个合适的互模拟关系S=σ，r，w∈R∞}⊆R∞×R∞，使得:

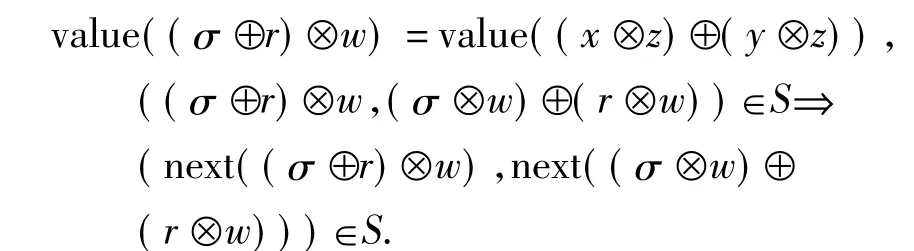
由⊕和⊗的定义有:

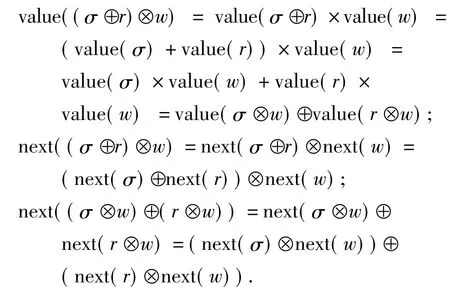
由假设可知((next(σ)⊕next(r))⊗next(w)，(next(σ)⊗next(w))⊕(next(r)⊗next(w)))∈S成立，即S是一个共代数互模拟，因此有(σ⊕r)⊗w=(σ⊗w)⊕(r⊗w).

对于终结共代数(vB，outB)，利用λ可将其提升为Fλ(vB，outB)=(FvB，FλoutB=λvB◦FoutB:FvB→BFvB)，且存在到终结共代数(vB，outB)的λ-Unfold射[FλoutB]B:FvB→vB，如图10 所示.

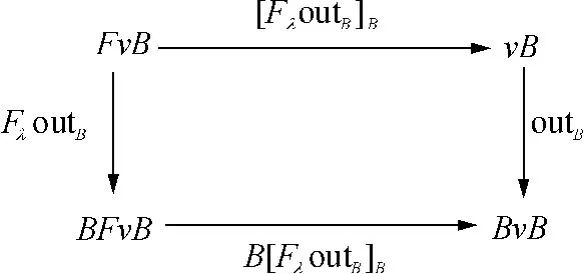
图10 终结共代数的λ-提升及λ-Unfold射Fig.10 λ-lifting andλ-Unfold morphisms of final coalgebras

定理4λ-Unfold射[FλoutB]B:FvB→vB是终结共代数(vB，outB)上的一个F-代数结构，且(vB，[FλoutB]B，outB)为一个λ-双代数，且为终结λ-双代数，而(vB，[FλoutB]B)为一个终结F-代数.

证明 由定理3的对偶性及图11的图表交换可容易证明.

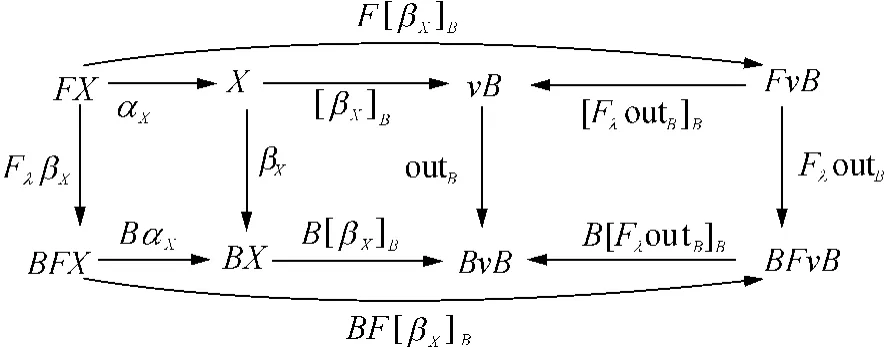
图11 FλβX到终结共代数的唯一射Fig.11 Unique morphism from FλβXto final coalgebras

上述定理给出了一种利用分配律λ:FB⇒BF及Unfold射构造终结共代数上的代数结构的方法，从而将终结共代数提升为终结λ-双代数.

3 结语

文中利用λ-双代数给出ADT的一种抽象描述，并分析其语法构造和动态行为的性质及两者间的关系.在此基础上，进一步利用分配律分别对共代数和代数函子进行函子化提升，给出一种构造初始代数(或终结共代数)上的共代数(或代数)结构，并将其提升为初始(或终结)λ-双代数的方法，从而扩展了代数中的归纳原理和共代数中的共归纳原理，并提高了程序语言对ADT中各种性质的描述与证明能力.

在下一步工作中，笔者将继续研究ADT上的其它递归(如原始递归、Course-of-Value迭代)和共递归(如原始共递归、Course-of-Value共迭代)函数，并探讨ADT上存在合适分配律的前提条件及其规范格式.

［1］Meijer E，Fokkinga M，Paterson R.Functional programming with bananas，lenses，envelopes and barbed wire［C］∥Hughes J.Functional Programming Languages and Computer Architecture.Berlin:Springer，1991:215-240.

［2］Malcolm G.Algebraic types and program transformation［D］.Groningen:Department of Computing Science，University of Groningen，1990:1-50.

［3］Bird R.Introduction to functional programming using Haskell［M］.2nd ed.London:Prentice-Hall，1998.

［4］苏锦钿，余珊珊.共归纳数据类型上的共递归操作及其计算定律［J］.华南理工大学学报:自然科学版，2011，39(10):90-95.Su Jin-dian，Yu Shan-shan.Corecursion operations and its calculation laws on coinductive data types［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(10):90-95.

［5］Hensel U，Jacobs B.Coalgebraic theories of sequences in PVS ［J］.Journal of Logic and Computation，1999，9(4):463-500.

［6］Hinze R.Reasoning about codata［C］∥Horváth Z，Plasmeijer R，Zsók V.Central European Functional Programming School(CEFP 2009).Berlin:Springer，2010:42-93.

［7］Hutton G.Fold and unfold for program semantics［C］∥Proceeding of 3rd ACM SIGPLAN International Conference on Functional Programming.New York:ACM Press，1998:280-288.

［8］Vene V，Uustalu T.Functional programming with apomorphisms(corecursion) ［J］.Proceedings of the Estonian Academy of Science:Physics，Mathematics，1998，47(3):147-161.

［9］Rutten J J M M，Turi D.Initial algebra and final coalgebra semantics for concurrency［C］∥Proceedings of REX School/Symposium.Berlin:Springer，1993:477-530.

［10］Turi D.Functorial operational semantics and its denotational dual［D］.Amsterdam:Department of Computer Science，Free University，1996:1-227.

［11］Turi D，Plotkin G D.Towards a mathematical operation semantics［C］∥Proceedings of 12th Symposium on Logic in Computer Science.Washington:IEEE，1997:280-291.

［12］Erwig M.Metamorphic programming:structured recursion for abstract data types［R］.Hagen:Computer Science Department，Fern University，1998:20-30.

［13］Erwig M.Categorical programming with abstract data types［C］∥7th International Conference on Algebraic Methodology and Software Technology.Berlin:Springer，1998:406-421.

［14］Nogueira P，Moreno-Navarro J J.Bialgebra views:a way for polytypic programming to cohabit with data abstraction［C］∥WGP'08 Proceedings of the ACM SIGPLAN workshop on Generic Programming.New York:ACM，2008:61-73.

［15］Rutten J J M M.Universal coalgebra:a theory of systems［J］.Theoretical Computer Science，2000，249(1):56-58.

［16］Bartels F.Generalised coinduction［J］.Electronic Notes in Theoretical Computer Science，2001，44(1):67-87.

［17］Bartels F.On generalised coinduction and probabilistic specification formats:distribute laws in coalgebraic modeling［D］.Amsterdam:Department of Computer Science，Free University，2004:42-43.