《工科数学分析》开放式教学探讨

杨小远, 李尚志, 孙玉泉, 薛玉梅, 杨卓琴, 杨义川

(北京航空航天大学数学与系统科学学院数学、信息与行为教育部重点实验室,北京 100191)

《工科数学分析》开放式教学探讨

杨小远, 李尚志, 孙玉泉, 薛玉梅, 杨卓琴, 杨义川

(北京航空航天大学数学与系统科学学院数学、信息与行为教育部重点实验室,北京 100191)

全面介绍了北京航空航天大学《工科数学分析》课程开放式教学的探索和实践.

课程建设;开放式教学;开放式作业

1 大学一年级学生面临的问题

对于刚刚走进大学的中学生来讲,大学的学习应该说是真正意义上学习的开始.中学期间数学的内容和知识面都是很浅的,但是由于高考竞争的残酷,中学期间的数学学习主要是大量的题海训练.在这个过程中,老师教会学生各种各样解题技巧,然后学生在进行类似问题题海训练,导致学生思维方式不开阔,喜欢套路子想问题,许多数学问题求解不是学生自己体悟出来,更多是教出来.每个中学生的背后都有一个强大的“团队”,这个团队有各科老师事无巨细的教学,各种家教等等,因此导致学生学习依赖性过强,自主性学习习惯没有养成,缺乏独立思考问题和对未知问题的探索能力.面临这些大学生,高等教育面临两个基本任务.一是从依赖性的学习方式到自主性学习方式的转变,二是从中学以做题为主的思维方式到形成开放思维方式的转变.《工科数学分析》实际上是从中学到大学转变学习方式和思维方式承上启下的一门课程,因此就目前面临的问题,我们就《工科数学分析》课程的教学内容、教学方式进行深层次的探讨和实践.

2 关于《工科数学分析》课程开放式教学的探索

我们授课学生的群体是工科专业的学生,如何加深数学教学内容,一直是我们面临的主要问题.对工科的学生来讲,他们更关心“数学有什么用,它能帮助我们解决什么问题”.因此在教学内容和教学模式上应该与传统数学系的学生有所区别.在工程应用领域真正需要用到的具体数学分支,具体的数学定理、公式和结论,其实并不很多,学校里学过的数学知识很多都似乎没有派上什么用处,但所受的数学训练,所领会的数学思想和精神,却无时无刻不在发挥着积极的作用,成为取得研究成功的最重要因素.数学是一门高度抽象的学科,但是它不是人类精神纯粹自由创造和想像,而是源于自然和工程问题.如果将教学仅仅看成是一般数学知识的传授,那么即使讲授再多的定理和公式,可能仍免不了沦为一堆僵死的教条,难以发挥作用,而掌握了数学的思想方法和精神实质,就可以由不多的几个公式演绎出千变万化的生动结论,显示出无穷无尽的威力.因此仅仅将数学作为知识来学习,而忽略了数学概念本质的背景就失去了开设数学课程的意义.在教学过程中除了教授经典课程内容以外,进行开放式教学的探索,增强数学应用背景的讲授,拓宽学生的知识面,了解数学学科在科学研究领域的重要性,为学生打开数学与应用的窗口.在整个课程的讲授过程中作了系列开放式讲座,我们以下面10个专题为例进行说明.这里详细介绍第一个专题讲座,其余概括性的介绍.这些讲座的主要特点都是以问题驱动的研究性教学.

i)Taylor公式与科学计算

Taylor公式是微积分的经典内容,为此我们为学生开设了《Taylor公式与科学计算》专题讲座.通过Taylor公式在导数数值计算的简单应用,阐述了Taylor公式科学计算中的应用.首先通过一个算例介绍计算机实现导数计算存在的问题.以问题驱动的教学,会激发学生对未知问题的探索能力和兴趣.

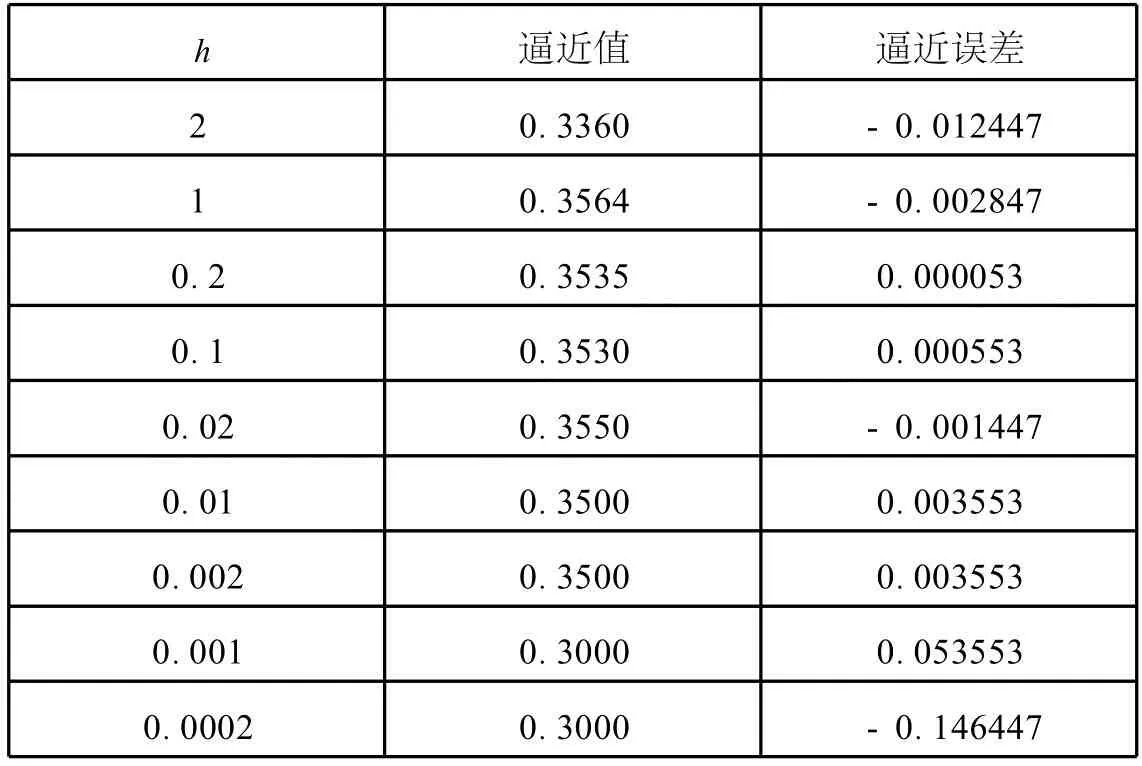
表1 导数计算结果

这里我们采用近的计算公式:

从表1我们发现:当h=0.2时计算效果最佳,h取得比0.2小时,计算的效果越来越差,学生看到这些计算实例,对计算结果感到很惊讶.这个现象与我们的设想有着“天壤之别”.按照导数的定义,h越小应该计算精度越高.原因是用计算机表示任何数字只能是有限位,因此任何运算都会有舍入误差,当h取得非常小时,上述公式出现两个相近数字相减,使得有效数字减少,因此导致表1的计算结果.面对这样的问题,如何解决?应用Taylor公式构造更高精度的计算公式,也即是计算数学领域著名的外推算法.

由Taylor公式,可以得到如下:

可见公式(2)比(1)提高了精度.用类似的方法构造序列:

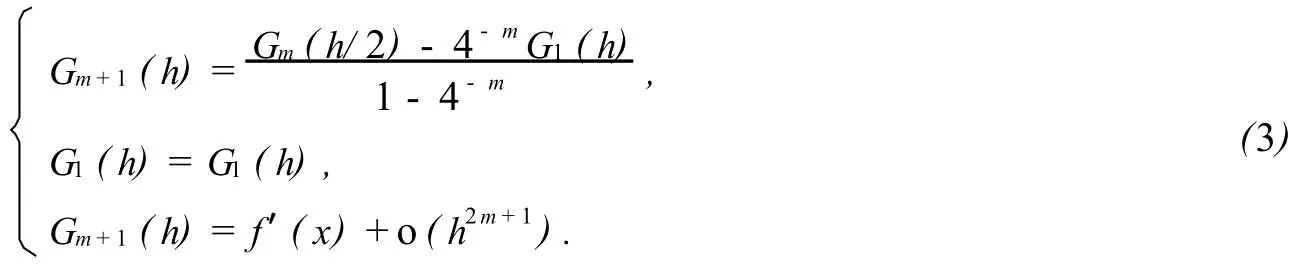
得到更精确的导数计算公式.我们展示给学生一个实际算例:

例2 计算f(x)=cotx在x=0.004导数值,其中f′(0.004)=625.33344002.

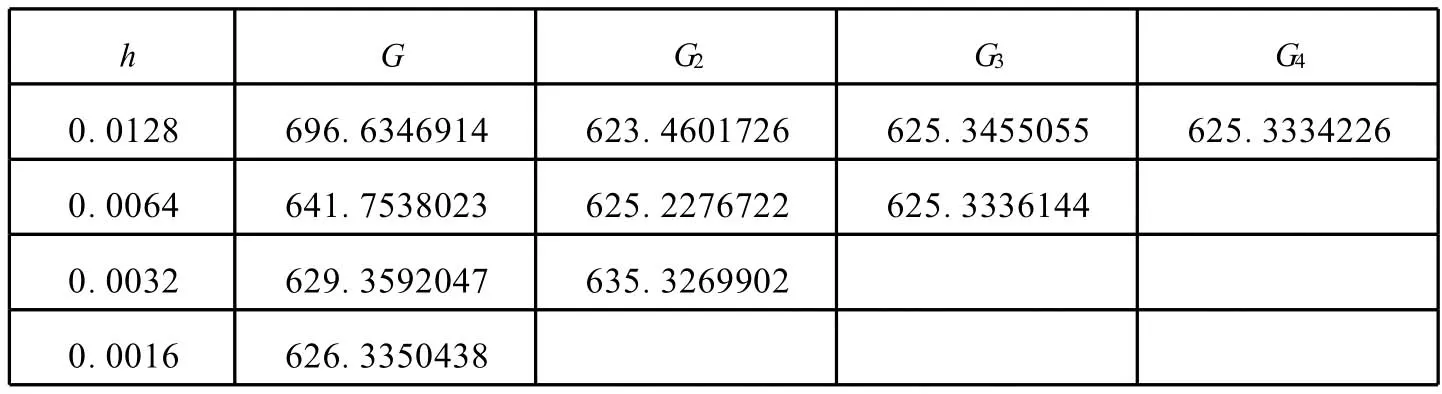
表2 导数的外推计算结果

从表2可以看出h=0.0016时,用(1)计算仅有二位有效数字,经过外推计算以后,G4有效数字达到了7位,因此大大提高了精度.学生对表2的计算结果非常感兴趣,感觉到获得了“不可思议"计算结果,体会到了数学在科学研究中的重要作用.

利用类似的思想,我们给出推广更一般结论,李查逊外推(Richardson).Richardson外推在科学计算领域中被广泛应用于研究高精度的算法.掌握了外推的思想以后,学生能够在高阶导数以及定积分的数值计算中实现高精度的数值算法.通过上面的教学实践,学生对Taylor公式有了全面深刻的认识并能够解决一些实际问题.通过讲座学生了解科学计算中必须充分重视舍入误差对计算结果的影响,这也是科学计算面临的重要研究课题.以问题驱动的研究性教学增强学生应用数学的能力.

ii)Taylor公式进一步思考——关于分段函数的应用

通过分析Taylor公式逼近函数的局限性,给出改进的几种逼近的思路和思想,包括拉格朗日插值和样条逼近等目前逼近论研究的几个问题,这些内容详细推导可以给学生推荐相关书籍,自己进一步学习.同学们认识到分段函数不是数学家杜撰出来的,是实际问题中需要这类特殊函数,实际上任何数学分支都不是人类纯粹的精神想像,而是来源于实际问题.

iii)连续函数压缩映射问题的讨论

在数学分析中有一经典习题,连续函数的压缩映射定理.我们引深教学内容,讲了不动点理论在非线性方程求根中的应用.我们给出许多实际的算例,让学生分析对不同的压缩映射函数,得到不同迭代方法的收敛速度问题.学生们利用无穷小阶的运算知识给出了几种收敛速度的定义.学生不仅加深对连续函数的认识,同时学会用无穷小阶运算描述数学问题.为了进一步开拓学生的思路,让学生有更多的想像空间,在课堂上介绍了如果不动点是一幅图像会怎么样?在此基础上我们介绍了不动点理论在分形图像压缩中的应用,阐明创新思想的重要性.

iv)从傅里叶级数谈起

傅立叶级数部分内容学生学起来,普遍感觉计算量大,对教学内容不感兴趣,学生们对一个简单的函数展成傅里叶级数感到“莫名奇妙”.在教学过程中作了一次专题讲座,主要内容如下：傅里叶级数提出的应用背景即傅里叶级数的根本意义.在傅里叶级数基础上,从离散到连续我们讲了傅里叶变换.在此基础上介绍傅里叶变换的缺点,更进一步,介绍了小波变换.在课堂上我们没有讲解具体的小波变换数学表达式,只讲解小波变换基本思想和它如何克服傅里叶变换的缺点.同时以汶川地震为例介绍傅里叶变换和小波变换在航空航天遥感图像分析与理解领域的应用.当我们从这样一个视角介绍傅里叶级数时,学生自然对傅里叶级数产生了兴趣.

v)极值问题中拉格朗日函数与优化理论初步

数学分析中极值问题中一个重要的结论是拉格朗日函数.在讲完多元函数极值基本理论方法以后.我们给出几个极值问题的例子.实际上这些例子最终都是求解一个非线性方程组.教材上的例题最终非线性方程组都可以求精确解.我们没有停留在这一点上,进一步给出一个复杂问题,相应的非线性方程组解析解求不出来,怎么办?因此我们介绍了数值优化理论这一计算数学重要分支.最优化理论的基本问题就是在拉格朗日函数基础上的数值求解,介绍目前研究现状和面临的挑战性问题.

vi)常微分方程数值计算

数学分析课程中常微分方程内容就几类典型方程求解析解,内容简单,学生容易理解和接受.我们在课堂上主要讲授了分离变量法和二阶线性方程组的解法.在此基础上我们介绍常微分方程的数值解法和一些基本问题,通过简单例子介绍常微分方程面临的一个挑战课题：刚性问题的求解.

vii)场论中一些数学问题

积分学的三大定理：GREEN定理,GAUSS定理,STOKES定理,学生就其数学形式普遍理解很好,但是在物理和力学应用背景下描述,往往很陌生.因此在教学中通过引入梯度算子,散度算子,旋度算子等和形式计算的技巧,让学生更深刻了解利用数学工具描述工程领域中问题的重要性.

viii)关于可积理论的进一步思考

函数积分的理论主要是如何判断一个函数满足什么样的条件是可积分的,一般的数学分析书主要讲授是达布上和与下和定理,但是这个定理并没有直观解释函数满足什么条件是可积分的.我们启发学生,连续函数可积,若有限个间断点可积,这些都可以证明.我们留给学生一个思考题目：函数到底有“多少”个间断点可积?学生一开始普遍认为只有有限个能保证可积.我们启发学生想如果间断点是在一个收敛数列,结论是否成立?学生证明了这个结论.在这个基础上我们初步介绍至多可数集合和零测集合等概念,在此基础上介绍Lebesgue定理和相应新的数学分支.很多学生对上述概念产生了浓厚的兴趣,他们了解数学学科的博大精深.通过这样的训练引导学生对科学问题的探索、钻研精神.

ix)关于柯西定理的进一步思考

数学分析课程中有数列收敛的柯西定理,函数极限存在的柯西定理,函数一致连续的柯西定理,数项级数收敛的柯西定理,函数项级数一致收敛的柯西定理,广义积分一致收敛的柯西定理.这些定理都是数学分析中的精彩内容.学生学习多了容易引起概念和理解的混乱.在学期末,我们让学生重新认识和理解柯西定理,讲解这些定理刻画问题的共性特征,学生的思路变得清晰和自然,同时我们要求学生想一想柯西定理就在我们身边应用的例子.

x)数学分析中“一致"概念的直观理解

数学分析中有一个重要的教学内容是有限次运算法则(极限运算、连续运算、可导运算、可积运算,广义积分运算)能否将有限次运算推广到无限次运算.这些教学的内容难点是“一致”概念,包括函数一致连续,函数序列和函数项级数的一致收敛,广义积分的一致收敛.对这部分内容的学习,学生感到“头疼”,最主要的原因是对这些概念没有真正理解.因此在讲解这些概念的同时,我们借助多媒体教学给学生大量一致连续函数和不一致连续函数的几何图像,使得学生从直观上理解一致连续函数和不一致连续函数的区别.对函数序列和函数项级数的一致收敛,广义积分的一致收敛也是同样的处理方法,让学生从根本上理解这些概念.在学生理解这些概念以后,在讲“一致”带给我们“好处”,也即是相应的基本理论和结论.

xi)微积分在实际问题中综合举例

适当增加了微积分在经济,生物,航空航天等应用领域的例子.通过这些综合应用类型的例题,将数学建模的思想引入教学过程,让学生体会解决一个实际问题的全过程：数学建模—求解方法—结果分析全过程.让学生感觉数学的亲切,不再是象牙塔里高不可攀的阳春白雪,数学就在我们身边.

尽管上面教学内容占据一些学时,可以通过对经典数学分析教学内容进行提炼,压缩一些学时,同时由于采用多媒体教学,因此开放式教学内容完全可以实现.

3 关于《工科数学分析》课程开放式作业的探索

数学是一门推理和思考型的学科.数学最富有吸引力也是最本质的就是她的思想.在教学过程中学习新的概念和知识时,要强调这些知识来源和数学家如何思考和解决问题,引导学生与数学大师思想对话.但是数学思想是不可能像填鸭那样灌输给学生.能否较好把数学思想介绍给学生,要求是双向的.既要求老师善于讲,也要求学生有兴趣,肯思考.著名科学家牛顿在被问到是什么使得他发现了万有引力定律时,其回答非常简单：“By thinking on it continually”.几乎所有的伟大发现都归功于不断的思考.爱因斯坦说过：“Imagination is more important than knowledge”.数学家韦尔斯(Andrew Wiles)十年磨一剑攻克费尔马大定理,就是从小就迷上了这个世界难题.物理学家弗里希(Frisch)“科学家必定有孩童般的好奇心,一个成功的科学家,必须保持这种孩提时的天性”.一些重要的数学理论和方法,在一开始往往是混乱粗糙、难以理解甚至不可思议的,经过许多乃至几代数学家的努力,有时甚至经过长期的激烈论争,才逐步去粗取精、去伪存真,最终才出现了现在为大家公认的系统的理论.数学教育要创造一种环境,使同学身临其境地介入数学的发现或创造过程,鼓励并推动学生解决一些理论或实际的问题.这些问题没有现成的答案,没有固定的方法,没有指定的参考书,甚至也没有成型的数学问题.主要靠学生独立思考、反复钻研并相互切磋,去形成相应的数学问题,进而分析问题的特点,寻求解决问题的方法.总之,让学生亲口尝一尝梨子的滋味,亲身去体验一下数学的创造过程对培养学生独立思考问题的能力是非常重要的.

在教学过程中,我们陆续给学生留一些开放式的作业如下：

1)欧拉常数是有理数或是无理数?(公开问题);

2)讨论一个有序代数结构完备性,阿基米德性,稠密性,加法交换律,加法结合律,乘法交换律,乘法结合律之间的关系;

3)结合实数完备性定理说明对极限定义及实数连续性的理解;

4)举新例说明数列及数列极限的应用;

5)压缩映射原理的进一步思考和应用;

6)利用Taylor定理讨论二阶导数的外推计算;建立π的快速收敛算法;

7)研究克服Taylor定理局部逼近更好的多项式逼近方法;

8)研究更精确的正项级数收敛判别方法;

9)关于Canchy定理的进一步思考,举例Canchy定理就在我们身边的例子;

10)若干微积分在经济、生物、天文等应用领域中的综合应用例题建模求解;

11)对教材中某些感兴趣的定理、习题的多种解法和更一般结论的探讨.

4 教学方法探讨

数学分析内容庞大,因此在教学过程中不要追求事无巨细和面面俱到,需要我们精讲核心和本质的内容.如果觉得教学内容个个重要,不分轻主次,反而使得学生不得要领.因此在教学过程中我们要注意许多共性的问题,提炼精华,这样才能使得学生学得精通.同时在教学过程中,注意给学生留出思考的空间,启发学生,促成养成思考的习惯.如果每堂课程80%的讲授内容,要留出20%的内容自学和思考.让学生随着课堂内容,与老师的教授同步进行思考,只有这样,才能培养学生不墨守成规,富于开拓精神,为学生创造一个有利于思考的环境.

5 结束语

本文全面介绍了我校《工科数学分析》课程开放式教学的探索和实践.鉴于文章的篇幅有限,没有附学生开放式作业.我们将在有关期刊陆续展示学生的开放式作业.在教学实践过程中,学生独立思考能力和推理能力正在逐步形成,学生的潜力是巨大的,通过高质量的本科教学,他们完全可以承担国家未来科技重任.

Opening Teaching and Practice for Mathematical Analysis

YA N G Xiao-yuan, L I S hang-zhi, SUN Yu-quan, XU E Yu-mei, YA N G Zhuo-qin, YA N G Yi-chuan
(School of Mathematics and System Sciences,Beihang University Xueyuan Road 37,Haidian District,Beijing 100191,China)

This paper fully introductions opening teaching and practice of mathematical analysis of engineering course of the Beijing University.

courses construction;open teaching;open problem

O13;G420

C

1672-1454(2011)03-0001-06

2009-12-17

北京市精品课程建设项目(430341);校重点教改项目《工科数学分析开放式教学研究与实践》