拟Koszul-like模＊

吕家凤, 包科维, 叶晓晓, 王一帆

(浙江师范大学数理与信息工程学院,浙江金华 321004)

0 引 言

Koszul代数最初由 Priddy[1]提出,它是一类具有许多优美同调性质且在数学的诸多分支均有重要应用的二次代数.Berger[2]首次把这类代数推广到高次代数上,引入了非二次的 Koszul代数,这类代数后来常被称为 D-Koszul代数[3-4].Green等[5]把 Koszul对象推广到非分次情形,讨论了诺特半完全代数的 Koszul性质和诺特半完全代数上的有限生成模的 Koszul性质,定义了拟 Koszul代数和拟 Koszul模.受文献[5]的启发,文献[6]研究了诺特半完全代数的D-Koszul性质,引入了拟 D-Koszul代数的概念;文献[7-8]讨论了诺特半完全代数上的有限生成模的 D-Koszul性质,定义了拟 D-Koszul模.而 Koszul-like代数和 Koszul-like模是 Koszul代数和 Koszul模的又一自然推广 (事实上,Koszul代数到目前为止已经有很多形式的推广,如文献[9-12]),且有例子表明,某些整体维数是 5的 Artin-Schelter正则代数是 Kos-zul-like代数.

本文主要把 Koszul-like模推广到非分次情形,讨论了诺特半完全代数上有限生成模的 Koszul-like性质,定义了拟 Koszul-like模,并试图把有关 Koszul-like模的一些好的性质推广到非分次情形.

1 Koszul-like模及其极小分次投射分解

其中,d,t1和 t2是满足 d>t2>t1>1的自然数.

定义 1 设 A是标准分次代数.称有限生成分次 A-模M为 Koszul-like模,如果 A-模 M有极小分次投射解

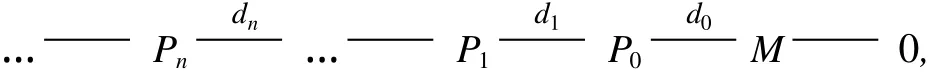
使得对于任意的 n≥0,Pn由δdt1,t2(n)次生成.特别地,若平凡 A-模 A0是 Koszul-like模,则称标准分次代数 A是 Koszul-like代数.

显然,对于 Koszul-like模,有如下判定方法:

命题 1 设A是标准分次代数,M是有限生成的非负分次A-模,则M是 Koszul-like模当且仅当对任

证明 类似于λ-Koszul模[11]的情形,故略.

命题 2[5]设A是标准分次代数,则存在有限箭向图Γ和路代数 kΓ的分次理想 I⊂∑n≥2(kΓ)n,使得作为分次代数,有 A≅kΓ/I成立.

定理 1 设 A=kΓ/I是标准分次代数,M是由 0次生成的分次 A-模.设

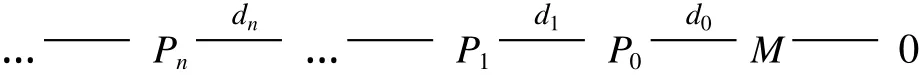
是 A-模M的极小分次投射分解,则M是由δdt1,t2定义的 Koszul-like模当且仅当对任意 n≥0,有 kerdn⊆

t1,t2(n+1)次生成矛盾.因此,x∈Jkerdn.

定义 2 设 R是诺特半完全代数,J是其 Jacobson根,M是有限生成的 R-模,则称M是拟 Koszul-like模当且仅当M有极小投射解

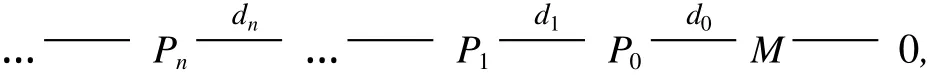
使得对任意的 n≥0,有

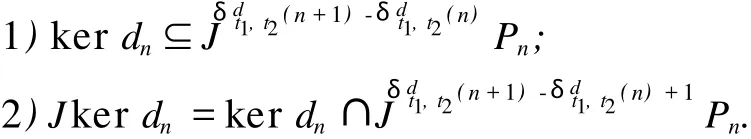
特别地,若 R/J是拟 Koszul-like模,则称 R是拟 Koszul-like代数.

例 1 1)局部正则代数[13]是拟 Koszul-like代数.事实上,令 R是局部正则代数,m是 R的极大理想,且 G(R)=n.设 x1,x2,…,xn是 R的一正则序列.通过常规计算,平凡模 R/m有如下极小投射分解:

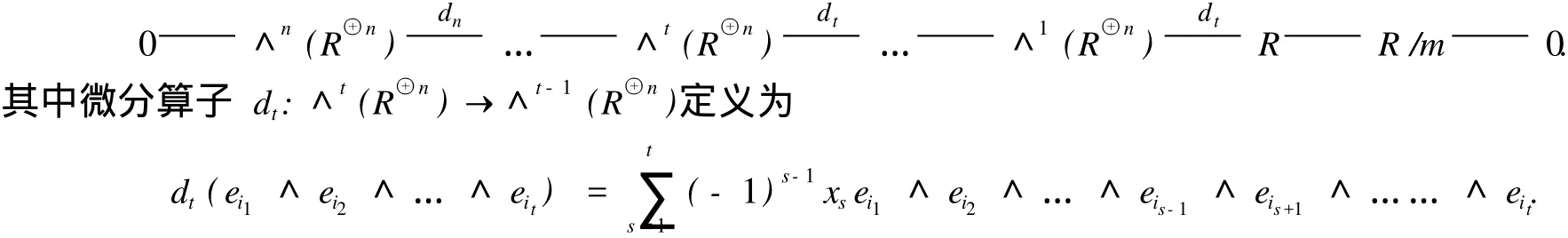
其中 e1,e2,…,en是 R⊕n的一组自由基.不难验证 R是拟 Koszul-like代数.

2)Green等在文献 [5]中定义的拟 Koszul代数 (模)是义的拟 Koszul-like代数 (模).

2 诺特半完全代数上的有限生成模

本节主要回顾诺特半完全代数上的有限生成模的基本性质,其中绝大部分内容可在文献[8]中找到,由于它在本文中具有重要作用,因此给出简要叙述.采用文献[8]中的记号,设 R是诺特半完全代数,J是 R的 Jacobson根,则对任意有限生成的 R-模M,必有如下投射分解:

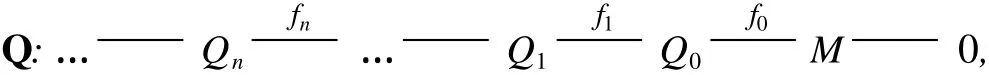
使得对任意的 n≥0,Qn是有限生成的 R-模且 kerfn⊆JQn,即分解 Q是“极小的”.为简洁起见,记 Si:=kerfi-1,常称 Si为 M的第 i个合冲.记

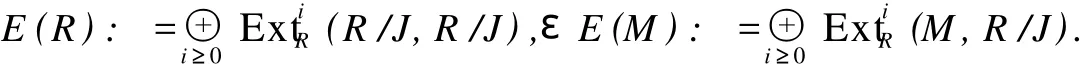
在 Yoneda积下,E(R)是分次代数,ε(M)作成分次 E(R)-模.值得注意的是,在本节的情形下,它们都不再是双分次的.然而,可以在ε(M)上定义第二次数

引理 1[8]采用上述记号,有下列命题成立:

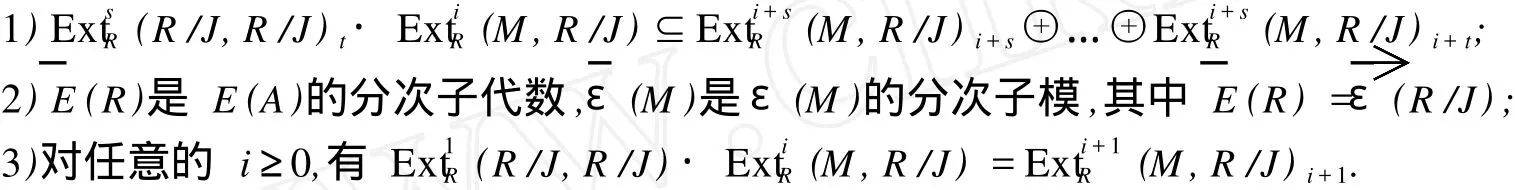
引理 2[8]设 R是诺特半完全代数,M是有限生成的 R-模,且

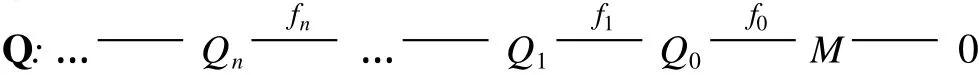
是M的极小投射解.令 f:N→N为任意一个满足 f(i)≥i≥1的递增的集合映射.则

3 拟 Koszul-like模的 Ext模

本节主要讨论如何用 Ext模刻画拟 Koszul-like模.

因此,对任意的 i≥1,δdt1,t2(i-1)=i-1,即M是拟 Koszul模.命题 3证毕.

注 1 命题 3表明,对于拟 Koszul-like模,没有类似于命题 1的结论,但仍然可以通过 Ext-模的第二次数刻画拟 Koszul-like的性质.

定理 2 设 R是诺特半完全代数,M是有限生成的 R-模,则M是拟 Koszul-like模当且仅当对任意的 i≥1,有

证明 必要性 设M是拟 Koszul-like模且

是M的极小投射分解.采用前面的记号 Si:=kerdi-1,则根据拟 Koszul-like模的定义,对任意的 i≥1,

即M是拟 Koszul-like模.定理 2证毕.

定理 3 设 R是诺特半完全代数,M是有限生成的 R-模.若有下列条件成立:

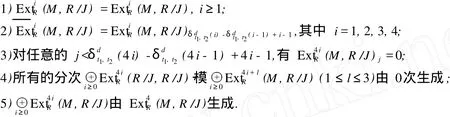
则M是拟 Koszul-like模.

综上,定理 3得证.

[1]Priddy S B.Koszul resolutions[J].TransAmerMath Soc,1970,152:39-60.

[2]Berger R.Koszulity for nonquadratic algebras[J].J Alg,2001,239(2):705-734.

[3]Green E L,Marcos E,Martínez-Villa R,et al.D-Koszul algebras[J].J Pure ApplAlg,2004,193(1/2/3):141-162.

[4]Cheng Zhi,Ye Yu.One-point extensions oft-Koszul algebras[J].ActaMath Sin:Engl Ser,2007,23(6):965-972.

[5]Green E L,Martínez-Villa R.Koszul and Yoneda-Ext algebras[J].Conference Proc AMS,1996,18:247-297.

[6]He Jiwei,Ye Yu.On the Yoneda-Ext algebras of semiperfect algebras[J].Alg Colloq,2008,15(2):207-222.

[7]吕家凤,冷雁.拟 d-Koszul模[J].浙江大学学报:理学版,2008,35(5):481-485.

[8]司君如.高阶拟 Koszul模[J].数学学报,2009,55(5):101-110.

[9]LüJiafeng.On moduleswithd-Koszul-type submodules[J].ActaMath Sin:Engl Ser,2009,25(6):1015-1030.

[10]LüJiafeng.On moduleswith piecewise-Koszul towers[J].Houston J Math,2009,35(1):187-205.

[11]LüJiafeng.Algebraswith periodic shifts of Ext degrees[J].Math Notes,2009,86(5/6):665-681.

[12]LüJiafeng,He Jiwei,Lu Diming.Piecewise-Koszul algebras[J].Sci China:A,2007,50(12):1795-1804.

[13]Weibel C A.An Introduction to HomologicalAlgebra[M].Cambridge:Cambridge Univ Press,1995.