随机变量函数教学中的思考

洪 沆

（黄山学院 数学系，安徽 黄山 245041）

随机变量函数教学中的思考

洪 沆

（黄山学院 数学系，安徽 黄山 245041）

讨论了连续型随机变量的函数所可能的类型,并给出连续型随机变量的函数是连续型随机变量的充分条件。

随机变量函数；连续型随机变量；绝对连续函数

1 连续型随机变量函数不一定是连续型随机变量

关于离散型随机变量与连续型随机变量，在教材中已给出了准确的定义，这两种类型的随机变量分布函数的性质是不一样的。离散型随机变量的分布函数只能是右连续的，而且分布函数的间断点为有限个或可列个，在所有间断点处的跳跃之和为1，而连续型随机变量的分布函数是连续的，利用分布函数的不同性质特征，往往可以作为判断随机变量是否是离散型的或是连续型的依据之一。下面我们所面临的问题是若ξ为连续型随机变量，f为定义在上R的函数，那么f(ξ)是何种类型的随机变量？

例 2：设ξ～N(0,1),f(x)=sgnx,x∈R,则随机变量函数η=f(ξ)是服从退化分布的随机变量,即P(η=0)=1，当然,η=f(ξ)是离散型随机变量。在该例中，f(x)是连续函数。事实上,我们还有更为一般的结果:若ξ为连续型随机变量,f(x)为常值函数,则f(ξ)服从退化分布。

例1，例2表明对于一般的函数甚至是连续函数而言,给定随机变量所对应的随机变量函数都未必是连续型的,如例1中的函数f(x)是非连续函数,而在例2中的函数f(x)则是连续函数,但是它们所对应的随机变量函数都是离散型的。那么连续型随机变量的函数有没有可能既不是离散型的也不是连续型的呢?下面的例子肯定了这一点。

例 3：设ξ～U(-1,1),f(x)=max{x,0},x∈R,显然 f(x)为连续函数,则η=f(ξ)既不是离散型的也不是连续型的。

事实上,由于η的分布函数

显然,Fη(x)不是连续函数,这说明 f(ξ)不是连续型随机变量。另外Fη(x)仅有唯一的跳跃点0,而在该跳跃点处跳跃,这说明随机变量函数η=f(ξ)既不是离散型的也不是连续型的。

2 连续型随机变量函数是连续型随机变量的条件

下面的问题是在什么条件下,连续型随机变量的函数是连续型随机变量呢?其实要回答这个问题,我们还要回到起点,即何谓连续型随机变量,一般的教材中都采用这样的定义:则称ξ是连续型随机变量。

事实上,按下面方式来定义连续型随机变量也是可以的:

（2）若随机变量ξ的分布函数F(x)所导出的可测空间(R,B(R))上的测度关于Lebesgue测度绝对连续, 则称ξ是连续型随机变量，这里B(R)表示R上的Borel集全体。

众所周知,由测度扩张定理,在(R,B(R))上,F(x)可以唯一地导出其上的概率测度,为简单记,仍将此概率测度记成F，另外假设(R,B(R))上的Lebesgue测度为m,若F≪m,即F关于Lebesgue测度m绝对连续,则由Radon-Nikodym定理可知,存在非负可积函数p(x),使得对任意的

（1）设随机变量ξ的分布函数为F(x),若存在非负可积函数p(x),使得对任意的x∈R,都有(2)是显然的,这说明(1)与(2)等价。

教材[1]中给出了连续型随机变量的函数是连续型随机变量的一个充分条件。

定理1：设ξ为连续型随机变量,其密度函数为p(x),又函数y=f(x)严格单调,其反函数h(y)有连续导数,则η=f(ξ)也是连续型随机变量,且其概率密度为

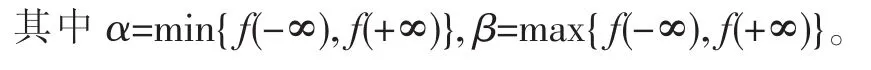
那么除了该定理之外,是否还有其他能判断连续型随机变量的函数为连续型随机变量的条件呢?在回答这个问题之前,我们先给出引理1：

引理1[4]：设f(x)定义在[a,b]上的绝对连续函数,E为Lebesgue测度为0的集合,则f(E∩[a,b])也是Lebesgue测度为0的集合。

按照（2）的定义方式,若要连续型随机变量ξ的函数f(ξ)为连续型随机变量,当且仅当∀E∈B(R1),m(E)=0,都有m(f-1(E))=m(h(E∩G)=0,其中m为(R,B(R))上的Lebesgue测度,h(y)为f(x)的反函数,G为f(x)的值域。

定理2：设ξ为连续型随机变量，f(x)为定义在R上的函数，其反函数h(y)存在，令h(y)在(α,β)的任何有限闭子区间上都是绝对连续的，则η=f(ξ)是连续型随机变量。

证：(1)若α,β皆是有限数,为简单记，不妨假设h(y)的定义域为＜α,β＞,其中＜α,β＞为(α,β)、[α,β]、[α,β)、(α,β]之一，则由引理 1 有

(2)若 α=-∞,β为有限数,假设h(y)的定义域为＜-∞,β＞,其中＜-∞,β＞为(-∞,β)或(-∞,β],由引理 1 有

类似地,可证明若α为有限数,β=+∞或α=-∞,β=+∞ 时,皆有m(f-1(E))=0，故η=f(ξ)是连续型随机变量。

定理3：设ξ为连续型随机变量，f(x)为定义在R上的函数其中I1、I2、…为一列互不相交的区间。令若f(x)在每个Ii上都存在反函数hi(y),且hi(y)在(αi,β)的任何有限子区间上都是绝对连续的,则η=f(ξ)是连续型随机变量。

证：与定理2的证明方法类似，略。

事实上,定理2是定理1的推广,这是由于函数f(x)若满足定理1的条件,则其反函数(α,β)在的任何有限闭子区间上都存在有界的导函数,从而满足李普希兹条件,故h(y)在(α,β)的任何有限闭子区间上都是绝对连续的。

[1]魏宗舒,等.概率论与数理统计教程[M].北京：高等教育出版社，1983：128-130.

[2]丁万鼎.测度论概要[M].合肥：安徽教育出版社，2005:69-78.

[3]程其襄,等.实变函数与泛函分析基础[M].北京：高等教育出版社，2003:160-161.

[4]I.P.Natanson,Theory of Functions of a Real Variable[M].Frederick Ungar Publishing Co,New York,1964:248-252.

Thoughts on the Teaching of Function of Random Variable

Hong Hang
(Department of Mathematics,Huangshan University,Huangshan245041,China)

In this paper,the possible types of function of continuous random variable are discussed,and a conclusion that function of continuous random variable is the sufficient condition for continuous random variable is drawn.

function of random variable;continuous random variable;absolutely continuous function

O211.4

A

1672-447X（2011）03-0098-002

收搞日期：2010-09-09

黄山学院教学研究项目（2008hsujy027）

洪沆（1972-），安徽黄山人，黄山学院数学系副教授，研究方向为概率论。

胡德明