格空间上算子方程组新的不动点定理

刘春晗，王建国

（齐鲁师范学院 数学系，山东 济南250013）

格空间上算子方程组新的不动点定理

刘春晗，王建国

（齐鲁师范学院 数学系，山东 济南250013）

在u0－r完备Archimedean型向量格中利用半序的方法研究了一类带有次线性扰动的算子方程组，在非紧非连续的假设下证明了不动点的存在唯一性，并给出了迭代误差估计式.

混合单调算子；次线性算子；u0－r完备Archimedean型向量格；迭代序列

0 引言及预备知识

其中算子A1具有某种凹性，A2具有某种凸性，算子B为次线性算子，并且得到了迭代唯一性定理.此类方程组研究较少，而且u0－r完备Archimedean型向量格只有半序结构，没有拓扑结构，不用对锥加正规的条件，也没有用到通常的范数，从而不同于以往的研究.

下面给出相关定义和引理：

定义1［5］E为序向量空间，E称为向量格（又称Riesz空间），若对任意的x，y∈E，存在它们的上确界x∨y和下确界x∧y，并且满足代数运算与序相容的条件：①对任意z∈E，从x≤y可推出x＋z≤y＋z；②如果x≥θ，而数λ≥0，则λx≥θ.

格E的有序区间形式为［x1，x2］＝ ｛x∈E，x1≤x≤x2｝的任何集合，其中x1≤x2（x1，x2∈E）.

定义2［5］E称为Archimedean型向量格，若E为向量格，P＝ ｛x∈E，x≥θ｝；对于 ∀n∈N，x∈P，y∈E有nx≤y，则x＝θ.

定义3［5］E为Archimedean型向量格，固定u0∈E，且u0≥θ，序列｛xn｝称为是u0－r收敛于x∈E，若存在数列εn→0，εn∈（0，∞），使得记为.序列｛xn｝称为是u0－r基本列，若存在数列εn↓0，使得当m≥n时，有

定义4［5］Archimedean型向量格E称为是u0－r完备的，若其中元素的任何u0－r基本列都是u0－r收敛的.

本文总假定E是u0－r完备Archimedean型向量格，P为E中的正元锥.定义半序“x≤y”：若yx∈P，则y≥x，其中P＝ ｛x∈E，x≥θ｝.若u0∈P＼｛θ｝，令Pu0＝ ｛x∈E∶∃λ（x）＞0，μ（x）＞0，使得λ（x）u0≤x≤μ（x）u0｝.

注2 若E是u0－r完备Archimedean型向量格，∀f，g∈E×E，其中f＝ （f1，f2），g＝ （g1，g2）.在E×E中我们定义f＋g＝（f1＋g1，f2＋g2），af＝（af1，af2），其中a∈R；定义f≤g是fk≤gk（k＝1，2），则易证得E×E也是u0－r完备Archimedean型向量格.

定义5［4］若算子B∶E→E，满足B（tx）≤t Bx，x∈P，t≥1，则称B为次线性算子.

定义6［4］设E1，E2是2个半序向量空间，算子T∶E1→E2称为是正的，即T≥0，若T（P1）⊂P2，其中P1，P2分别是E1，E2中的锥.

定义7［6］设D⊂E，D×D⊂E×E，二元算子A∶D×D→E，则：①如果A（x，y）关于x非减，关于y非增，即对任何xi，yi∈D，i＝1，2.若x1≤x2，y2≥y1，则A（x1，y2）≤A（x2，y1），称A为混合单调的.②如果∈D，满足＝A（，），则称是A的不动点.

定义8［6］A∶P→E，称A为u0凹算子，如果满足条件：①∀x＞θ，Ax∈Pu0；②∀x∈Pu0，∀0＜t＜1，∃η（t，x）＞0，使得A（tx）≥ ［t（1＋η（t，x））］Ax.

定义9［6］设E为向量格，D为E中1个凸集，算子A∶D→E，则：① 若A（tx＋（1－t）y）≥tAx＋（1－t）Ay，∀x，y∈D，x≤y，0≤t≤1，称A为D 的凹算子.② 若A（tx＋（1－t）y）≤tAx＋（1－t）Ay，∀x，y∈D，x≤y，0≤t≤1，称A为D 的凸算子.

定义10［6］设A∶D ⊂E→E，0≤α＜1.称A为α凹（（－α）凸）算子，如果满足A（tx）≥tαAx（A（tx）≤t－αAx），∀x∈D，t∈ （0，1）.

引理1［7］设 ∀u0，z0∈P，｛xn｝是u0－r和z0－r基本列，则｛xn｝是u0－r收敛的充分必要条件是｛xn｝是z0－r收敛，且收敛点是相同的.

引理2［7］若E是u0－r完备的，对于任意固定的z0∈Pu0，则E是z0－r完备的.

引理3［8］E是Archimedean型向量格当且仅当 ∀u∈P，εn↓0，有εnu↓θ，即

引理4［7］设E是Archimedean型向量格，对任意固定的z0∈P，｛xn｝∈E∶①若，且，则x≥y；②若，且xn≤y，∀n∈N，则x≤y.

引理5［7］若E是Archimedean型向量格，对于任意固定的z0∈P，若｛xn｝∈E是单调上升z0－r基本序列，则｛xn｝是z0－r收敛到x∈E当且仅当｛xn｝有上确界，且；若｛xn｝∈E是单调下降z0－r基本序列，则｛xn｝是z0－r收敛到x ∈E 当且仅当｛xn｝有下确界，且

1 主要结果及其证明

定理1 设 w0∈P，v0∈Pu0， w0≤v0，算子A1，A2∶P×P→P是混合单调的，且B∶E→E是次线性算子.假设下列条件满足：

1）对固定的y，A1（·，y）∶P →E是u0凹算子，其中特性函数是η（t，x）∶（0，1）×［ w0，v0］→ （0，＋∞），而对固定的x，A2（x，·）∶P→E是－α凸算子，其中η（t，x）满足：① 函数η（t，x）关于x单调，关于t是左下半连续的；② 对任意（t，x）∈ （0，1）×［ w0，v0］，都有

2）算子I－B的逆算子（I－B）－1∶E→P存在，且在P上为正算子.

3）存在ε＞0，使 w0≥εv0，且A1（ w0，v0）≥ w0，A2（v0， w0）≤v0， w0≥B w0≥θ，Bv0≤θ.

4）A1（w，v）≤A2（v，w）≤A1（v，w），∀w，v∈ ［ w0，v0］， w≤v.

则方程（1）在［ w0，v0］中有唯一正解x＊，而且对以（x0，y0）∈ ［ w0，v0］×［ w0，v0］为初值的迭代序列

证明 令C1＝ （I－B）－1A1，C2＝ （I－B）－1A2，由条件2）和3）得：

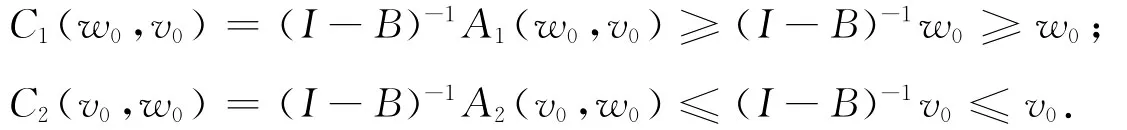
因为B为P上的次线性算子，故（I－B）－1为P上的次线性算子.事实上，对∀t≥1，x∈P，有（IB）（tx）≥t（I－B）x.再由（I－B）－1为P上的正算子，故（I－B）［t（I－B）－1x］≥t（I－B）（I－B）－1x＝tx，即（I－B）－1（tx）≤t（I－B）－1x；所以（I－B）－1为P上的次线性算子，并且可以证明对于 ∀t∈ （0，1），x∈P，（I－B）－1（tx）≥t（I－B）－1x.由条件2）易证得C1，C2为P上的混合单调算子.

下面证明对固定的y，C1（·，y）∶Pu0→E是u0凹算子，对固定的x，C2（x，·）∶P→E是－α凸算子.

1）事实上，因为（I－B）－1为次线性算子，所以对固定的y∈P及 ∀t∈（0，1），x∈Pu0，有C1（tx，y）＝ （I－B）－1A1（tx，y）≥ （I－B）－1［t（1＋η（t，x））A1（x，y）］≥t（1＋η（t，x））（I－B）－1A1（x，y）＝t（1＋η（t，x））C1（x，y）.

令 wn＝C1（ wn－1，vn－1），vn＝C2（vn－1， wn－1），n＝1，2，3，….由C1，C2为混合单调算子和条件4）可得对 ∀n∈N，有 w0≤ w1≤…≤ wn≤…≤vn≤…≤v1≤v0.再由条件3）易知 w1≥εv1，则 wn≥εvn.令则 wn≥tnvn.由 wn＋1≥ wn≥tnvn≥tnvn＋1，知0＜ε≤t1≤t2≤… ≤tn≤…≤1，从而存在，且ε≤t＊≤1.

下证t＊＝1.因为v0∈Pu0，εv0≤ w0≤v0，可得 w0∈Pu0，故 wn，vn∈ ［ w0，v0］⊂Pu0，所以.由此可得tn＋1≥.当η（t，x）关于x单减时；当η（t，x）关于x单增时，tn＋1≥.令n→ ∞，则

但由条件1）中的 ② 可得，当t＊∈ ［ε，1）时，（3）式均不成立，故t＊＝1.由t＊＝1知，limn→∞tn＝1.于是对∀p∈N有

由此可知｛ wn｝，｛vn｝都是v0－r基本列.由引理2可知E是v0－r完备的，所以存在w＊，v＊∈E使得.由引理5知 wn≤w＊≤v＊≤vn，从而因为E是Archimedean型向量格，由引理3可知当（1－tn）↓0时，有（1－tn）v0↓θ.因此，即v＊＝w＊.令x＊＝v＊＝w＊，则有

类似上面的证明可得C2（x＊，x＊）＝C1（x＊，x＊）.再由引理4可得x＊≤C1（x＊，x＊）＝C2（x＊，x＊）≤x＊，故C1（x＊，x＊）＝C2（x＊，x＊）＝x＊.由 wn≤x＊≤vn，易知x＊∈Pu0，故x＊为方程组（1）在Pu0中的不动点.

推论1 设 w0∈P，v0∈Pu0， w0≤v0，算子A∶P×P→P是混合单调的，且B∶E→E是次线性算子，假设下列条件满足：

而他的《隋唐演义》，好多人的出身和结局，和其他评书名家和小说都不一样，罗士信是在扬州战死的，秦琼的妻子是贾氏而不是通行的张氏，尤其他给秦琼配了一个特别长的绰号。而《童林传》是他根据《雍正剑侠图》的故事，自己编出来的一部书，与民国时评书名家常杰淼的著作，和后来李鑫荃的改编本都不一样。《乱世枭雄》里面，他说张作霖，让人头一回知道东北“胡子”（土匪）的形象，听他满嘴里“啪啪啪”的枪声，和“胡子”的黑话与做派。他结合了大量史料和传说，讲述张作霖枭雄的一生，给其安了个红颜知己田小凤。这人物是全虚构，那时候张学良还在世，给这么近的人物加故事，能把人说得不挑眼，直让人想做点版本学考证。

1）对固定的y，A（·，y）∶P→E是u0凹算子，其中特性函数是η（t，x）∶（0，1）×［ w0，v0］→ （0，＋∞），而对固定的x，A（x，·）∶P→E是－α凸算子，其中η（t，x）满足：① 函数η（t，x）关于x单调，关于t是左下半连续的；② 对 ∀（t，x）∈ （0，1）×［ w0，v0］，都有

2）算子I－B的逆算子（I－B）－1∶E→P存在，且在P上为正算子.

3）存在ε＞0，使 w0≥εv0，且A（ w0，v0）≥ w0，A（v0， w0）≤v0， w0≥B w0≥θ，Bv0≤θ.

则方程A（u，u）＋Bu＝u在［ w0，v0］中有唯一正解x＊，而且对以（x0，y0）∈ ［ w0，v0］×［ w0，v0］为初值的迭代序列xn＝ （I－B）－1A（xn－1，yn－1），yn＝ （I－B）－1A（yn－1，xn－1），n＝1，2，3，…，有

证明 在定理1中令A1＝A2即可得证.

定理2 设 w0，v0∈Pu0， w0≤v0，算子A1，A2∶P×P→P是混合单调的，且B∶E→E是次线性算子.假设下列条件满足：

1）对固定的y，A1（·，y）∶P→E是u0凹算子，其中特性函数是η（t，x），而对固定的x，A2（x，·）∶P→E是凸算子，其中η（t，x）满足：①函数η（t，x）关于x单调，关于t是左下半连续的；②存在使A1（w0，v0）≥εA2（v0，θ），对 ∀（t，x）∈ ［ε，1）×［ w0，v0］，都有

2）算子I－B的逆算子（I－B）－1∶E→P存在，且在P上为正算子.

3）A1（ w0，v0）≥ w0，A2（v0， w0）≤v0， w0≥B w0≥θ，Bv0≤θ.

4）A1（w，v）≤A2（v，w）≤A1（v，w），∀w，v∈ ［ w0，v0］， w≤v.

则方程组（1）在［ w0，v0］中有唯一正解x＊，而且对以（x0，y0）∈ ［ w0，v0］×［ w0，v0］为初值的迭代序列（2）式，有

证明 类似于定理1的证明可证得对固定的x，C2（x，·）∶P→E是凸算子.除证明t＊＝1时与定理1不同外，其余证明相同.下证t＊＝1.易证C1（ w0，v0）≥εC2（v0，θ），且有 wn，vn∈ ［ w0，v0］⊂Pu0，故wn＋1＝C1（wn，vn）≥C1（tnvn，vn）＝tn（1＋η（tn，vn））C1（vn，vn）≥tn（1＋η（tn，vn））C2（vn，vn）≥tn（1＋，所以.当η（t，x）关于x单减时当η（t，x）关于x单增时，tn＋1≥ （1＋η（tn， w0））×.令n→∞，则

由条件1）中的 ② 可得，当t＊∈ ［ε，1）时，（4）式均不成立，故t＊＝1.

推论2 设 w0，v0∈Pu0， w0≤v0，算子A∶P×P→P是混合单调的，且B∶E→E是次线性算子.假设下列条件满足：

1）对固定的y，A（·，y）∶P→E是u0凹算子，其中特性函数是η（t，x），而对固定的x，A（x，·）∶P→E是凸算子，其中η（t，x）满足：①函数η（t，x）关于x单调，关于t是左下半连续的；②存在使都有

2）算子I－B的逆算子（I－B）－1∶E→P存在，且在P上为正算子.

3）A（ w0，v0）≥ w0，A（v0， w0）≤v0， w0≥B w0≥θ，Bv0≤θ.则方程A（u，u）＋Bu＝u在［w0，v0］中有唯一正解x＊，而且对以（x0，y0）∈ ［w0，v0］×［w0，v0］为初值的迭代序列xn＝ （I－B）－1A（xn－1，yn－1），yn＝ （I－B）－1A（yn－1，xn－1），n＝1，2，3，…，有

证明 在定理2中令A1＝A2即可得证.

［1］吴焱生，李国祯.混合单调算子不动点存在唯一性定理及其应用［J］.数学学报，2003，46（1）：161－166.

［2］张石生，王凡，袁家纬.Banach空间中混合单调算子方程组解的存在性及其应用［J］.四川大学学报：自然科学版，1996，33（2）：215－218.

［3］贾娜，左黎明，郑雄军.一类混合单调算子方程组解的存在和唯一性定理［J］.江西科学，2006，24（5）：280－282.

［4］Li K，Liang J，Xiao T J.Ne wexistence and uniqueness theorems of positive fixed points for mixed monotone operators with perturbation［J］.J Math Anal Appl，2007，328（2）：753.

［5］刘证，郑权，张云生译.泛函分析：上册［M］.北京：高等教育出版社，1982：409－420.

［6］郭大钧.非线性分析中的半序方法［M］.济南：山东科学技术出版社，2000：54－70.

［7］刘春晗，王峰，王鑫.格α（t）凹凸算子的不动点定理［J］.徐州师范大学学报：自然科学版，2008，26（3）：43－47.

［8］Luxembubg W A J，Zaanen A C.Riesz Spaces：Volume I［M］.London：North－Holland Publishing Company，1971：280－287.

［9］许绍元，曾超益，朱传喜.φ凹 －（－ψ）凸混合单调算子不动点存在唯一性及其应用［J］.数学学报，2005，48（6）：1055－1064.

［10］Zhang Z T.Ne wfixed point theorems of mixed monotone operators and applications［J］.J Math Anal Appl，1996，204：307－319.

［11］孙经先.非线性泛函分析及其应用［M］.北京：科学出版社，2007：108－112.

［12］郭大钧.非线性泛函分析［M］.济南：山东科学技术出版社，1985：278－289.

Ne wtheorems of fixed points for systems of operator equations in vector lattice

LIU Chun－han，Wang Jian－guo
（DepartmentofMathematics，QiluNormalUniversity，Jinan250013，China）

By using the partial order method，we discuss the existence and uniqueness of solutions of a class of systerms of mixed monotone operator equations with sublinear perturbation without any compactness or continuity conditions inu0－rcomplete Archimedean vector lattice，and the iteration sequences which converge to solution of operator equations and the error estimates are given.

mixed monotone operator；sublinear operator；u0－rcomplete Archimedean vector iattice；iterative order

O177.91

A

1004－4353（2012）01－0007－06

2011－12－20

刘春晗（1981—），男，讲师，研究方向为非线性泛函分析及其应用.

国家自然科学基金资助项目（10971179）；山东省高等学校科技计划项目（J09LA55）；齐鲁师范学院青年教师科研基金资助项目（2011L1508）